Мартыненко Б.К. Языки и трансляции
Подождите немного. Документ загружается.


230
тогда и только тогда, когда A
→ x
0
B
1
x
1
...B
m
x
m
, y
0
B
1
y
1
...B
m
y
m
— правило из R, а
правило A
→ x
0
B
1
x
1
...B
m
x
m
есть правило номер i входной LR(k)-грамматики. Не-
трудно доказать, что (
π, y
R
) ∈τ(T
’
) тогда и только тогда, когда (S, S)
(w, y).
Схема T
’
— это простая sdts, основанная на LL(1)-грамматике, и, следова-
тельно, ее можно реализовать посредством dpdt P
3
.
На четвертом уровне dpdt P
4
просто обращает цепочку y
R
— выход P
3
,
запи-
сывая его в магазин типа first-in-last-out, а затем выдавая цепочку y из магазина
на свой выход.
Число основных операций, выполняемых на каждом уровне, пропорцио-
нально длине цепочки w. Таким образом, можно сформулировать следующий
результат:
Теорема 3.9. Трансляция, задаваемая простой семантически однозначной
схемой синтаксически управляемой трансляции с входной LR(k)-грамматикой,
может быть реализована за время, пропорциональное длине входной цепочки.
Доказательство представляет собой формализацию вышеизложенного.
§ 3.10. LALR(k)-Грамматики
На практике часто используются частные подклассы LR(k)-грамматик, ана-
лизаторы для которых имеют более компактные управляющие таблицы по срав-
нению с таблицами канонического LR(k)-анализатора. Здесь мы определим один
из таких подклассов грамматик, называемых LALR(k)-грамматиками.
Определение 3.17. Ядром LR(k)-ситуации [A →β
1
.β
2
, u] назовем A→β
1
.β
2
.
Определим функцию CORE(
A ), где A — некоторое множество LR(k)-ситуаций,
как множество ядер, входящих в состав LR(k)-ситуаций
из A.
Определение 3.18. Пусть G — контекстно-свободная грамматика, S —
каноническая система множеств LR(k)-ситуаций для грамматики G и
S’={A’|A’= { | CORE( ) = CORE( )}, .}
∈
∈
∪
B S
BB AAS
Если каждое множество
A’∈S’— непротиворечиво, то G называется
LALR(k)-грамматикой.
Другими словами, если слить все множества LR(k)-ситуаций с одинаковыми
наборами
ядер в одно множество и окажется, что все полученные таким образом
множества LR(k)-ситуаций непротиворечивы, то G — LALR(k)-грам-матика.
Число множеств, полученных при слиянии, разве лишь уменьшится. Соответст-
венно уменьшится число LR(k)-таблиц. Последние строятся обычным образом
по объединенным множествам LR(k)-ситуаций. Очевидно, что корректность
LALR(k)-анализатора, использующего таким образом полученные LR(k)-
таблицы, не нуждается в доказательстве.
Пример 3.15. Проверим, является ли рассмотренная ранее LR(1)-грам-
матика с правилами 0) S
’
→ S, 1) S → SaSb, 2) S →ε LALR(1)-грамматикой.
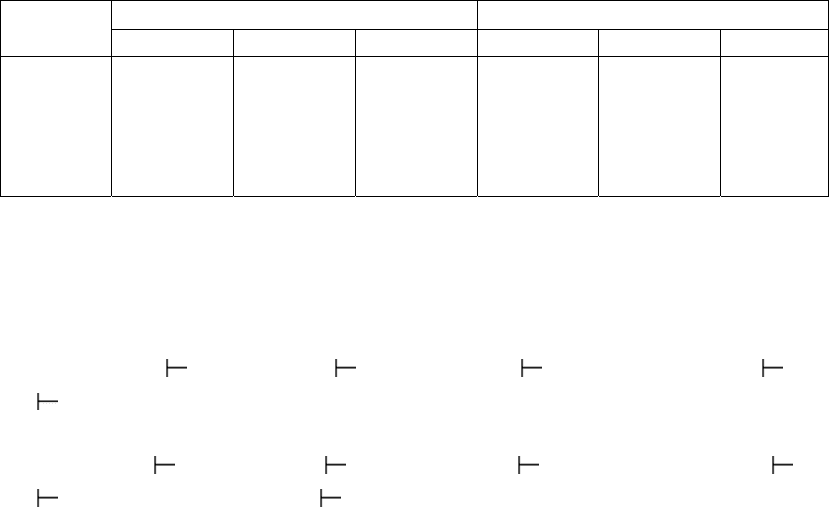
231
Каноническая система множеств LR(1)-ситуаций для нее была построена в
примере 3.10:
A
0
={[S
’
→ .S, ε], [S→.SaSb, ε | a], [S → ., ε | a]};
A
1
={[S
’
→ S., ε], [S→S.aSb, ε | a]};
A
2
={[S→Sa.Sb, ε | a], [S→.SaSb, a | b], [S → ., a | b]};
A
3
={[S→SaS.b, ε | a], [S→ S.aSb, a | b]};
A
4
= {[S → Sa.Sb, a | b], [S → .SaSb, a | b], [S → ., a | b]};
A
5
= {[S → SaSb., ε | a};
A
6
= {[S → SaS.b, a | b], [S → S.aSb, a | b]};
A
7
= {[S → SaSb., a | b]}.
Ясно, что в приведенной системе можно слить множества
A
2
и A
4
:
A
24
= A
2
∪A
4
= {[S → Sa.Sb, ε | a | b], [S → .SaSb, a | b], [S → ., a | b]},
множества
A
3
и A
6
:
A
36
= A
3
∪A
6
= {[S → SaS.b, ε | a | b], [S → S.aSb, a | b]},
а также множества
A
5
иA
7
:
A
57
= A
5
∪A
7
= {[S → SaSb., ε | a | b}.
Полученные множества
A
24
,
A
36
и A
57
— не противоречивы. Системе
объединенных множеств LR(k)-ситуаций соответствует управляющая таблица
(табл. 3.6).
Табл. 3.6
f(u) g(X) LR(1)-
таблицы
a b
ε
S a b
T
0
reduce 2 reduce 2 T
1
T
1
shift accept T
24
T
24
reduce 2 reduce 2 T
36
T
36
shift shift T
24
T
57
T
57
reduce 1 reduce 1 reduce 1
Отметим, что анализатор, использующий LALR(k)-таблицы, может чуть за-
паздывать с обнаружением ошибки по отношению к анализатору, использую-
щему каноническое множество LR(k)-таблиц. Например, канонический LR(1)-
анализатор для рассматриваемой грамматики обнаруживает ошибку в цепочке
abb, достигнув пятой конфигурации:
(T
0
, abb, ε) (T
0
ST
1
, abb, 2)
(T
0
ST
1
aT
2
, bb, 2)
(T
0
ST
1
aT
2
ST
3
, bb, 22)
(T
0
ST
1
aT
2
ST
3
bT
5
, b, 2 2) ,
а LALR(1)-анализатор
— на шестой:
(T
0
, abb, ε)
(T
0
ST
1
, abb, 2)
(T
0
ST
1
aT
24
, bb, 2)
(T
0
ST
1
aT
24
ST
36
, bb, 22)
(T
0
ST
1
aT
24
ST
36
bT
57
, b, 22)
(T
0
ST
1
, b, 221).

232
Приложение
НЕРАЗРЕШИМЫЕ И РАЗРЕШИМЫЕ ПРОБЛЕМЫ,
КАСАЮЩИЕСЯ ФОРМАЛЬНЫХ ЯЗЫКОВ
Здесь мы перечислим без доказательств алгоритмически неразрешимые и
разрешимые проблемы, относящиеся к различным свойствам формальных языв.
П.1. Неразрешимые проблемы
Контекстно-зависимые языки. Проблема пустоты: дана контекстно-
зависимая грамматика G. Вопрос: L(G)=∅?
Контекстно-свободные языки.
Проблема пустоты пересечения: даны произвольные контекстно-сво-
бодные грамматики G
1
и G
2
. Вопрос: L(G
1
) ∩L(G
2
)= ∅?
Проблема полноты: дана контекстно-свободная грамматика G, словарь
терминалов которой есть Σ. Вопрос: L(G )=Σ
*
?
Проблемы отношений между контекстно-свободными языками и
регулярными множествами: даны контекстно-свободная грамматика G и
регулярное множество R. Вопросы:
1) L(G) = R?
2) L(G) ⊇ R?
3) )(GL = ∅?
Проблемы
эквивалентности и вложенности: даны контекстно-свобод-
ные
грамматики G
1
и G
2
. Вопросы:
1) L(G
1
) = L(G
2
)?
2) L(G
1
) ⊆ L(G
2
)?
Проблема принадлежности пересечения классу контекстно-
свободных языков: даны контекстно-свободные
грамматики G
1
и G
2
. Вопрос:
L(G
1
) ∩ L(G
2
) — контекстно-свободный язык?
Проблема принадлежности дополнения классу контекстно-
свободных языков: дана контекстно-свободная
грамматика G. Вопрос: )(GL
— контекстно-свободный язык
?
Проблема регулярности языка: дана контекстно-свободная грамматика
G. Вопрос: L(G) — регулярное множество?
Неоднозначность контекстно-свободных грамматик и языков.
Неоднозначность контекстно-свободных грамматик: дана произ-
вольная контекстно-свободная грамматика
G. Вопрос: G — однозначна?

233
Проблема существенной синтаксической неоднозначности
контекстно-свободных языков: дана произвольная контекстно-свободная
грамматика G. Вопрос: L(G) — существенно однозначен?
Детерминированные контекстно-свободные языки. Проблемы соот-
ношения между детерминированными контекстно-свободными языками. Даны
языки L
1
и L
2
, принимаемые детерминированными магазинными автоматами.
Вопросы:
1) L
1
∩ L
2
= ∅?
2) L
1
∩L
2
— контекстно-свободный язык?
3) L
1
∪L
2
— детерминированный?
4) L
1
⊆L
2
?
П.2. Разрешимые проблемы,
касающиеся детерминированных
контекстно-свободных языков
Некоторые вопросы, которые не разрешимы для контекстно-свободных язы-
ков в общем случае, разрешимы для детерминированных языков. Например, да-
ны детерминированный контекстно-свободный язык L и регулярное множество
R. Разрешимы следующие вопросы:
1) L — существенно неоднозначен?
2) L = R?
3) L — регулярное множество?
4)
L = ∅?
5)
L — контекстно-свободный язык?
6)
L ⊇ R?
Нерешенная проблема — неизвестно, разрешима или нет следующая про-
блема: даны детерминированные магазинные автоматы
M
1
и M
2
. Вопрос: T(M
1
) =
T(M
2
)?
234
УКАЗАТЕЛЬ ЛИТЕРАТУРЫ
1. Greibach S.A. A note on undecidable properties of formal languages // Math. Systems Theory.
1968. Vol. 2, №1. P.1–6.
2. Hopcroft J.E., Ullman J.D. Formal languages and their relation to automata. — Reading, MA:
Addison-Wesley Pub. Co., Inc., 1969. 242 p.
3. Rozenberg G., Salomaa A. Handbook of Formal Languages. — Berlin, Heidelberg: Springer-
Verlag, 1997. Vol.1: 873 p., Vol. 2: 528 p., Vol. 3: 625 p.
4. Salomaa A. Formal languages. — N.Y.: Academic Press, 1973. 335 p.
5. Агафонов В.Н. Синтаксический анализ языков программирования: Учеб. пособие. —
Новосибирск: Изд-во НГУ, 1981. 91 с.
6. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Т. 1:
Синтаксический анализ. 612 с.; Т.2: Компиляция. 487 с. — М.: Мир, 1978.
7. Братчиков И.Л. Синтаксис языков программирования. — М.: Наука, 1975. 232 с.
8. Гинзбург С. Математическая теория контекстно-свободных языков. — М.: Мир, 1970. 326 с.
9. Гладкий А. В. Формальные грамматики и языки. — М.: Наука, 1973. 368 с.
10. Грис Д. Конструирование компиляторов для цифровых вычислительных машин. — М.:
Мир, 1975. 544 с.
11. Гросс М., Лантен А. Теория формальных грамматик. — М.: Мир, 1971. 294 с.
12. Кнут Д. Искусство программирования для ЭВМ. Т.1. — М.: Мир, 1976. 735 с.
13. Льюис Ф., Розенкранц Д., Стирнз Р. Теоретические основы проектирования компилято-
ров. — М.: Мир, 1979. 654 с.
14. Рейуорд-Смит В. Дж. Теория формальных языков: Вводный курс. — М.: Радио и связь,
1988. 129 с.
15. Саломаа А. Жемчужины теории формальных языков. — М.: Мир, 1986. 159 с.
16. Семантика языков программирования: Сб. статей под ред. А.Н.Маслова и Э.Д.Стоцкого —
М.: Мир, 1980. 394 с.
17. Фитиалов С.Я. Формальные грамматики. — Л..: Изд-во Ленингр. ун-та, 1984. 99 с.
18. Фостер Дж. Автоматический синтаксический анализ. — М.: Мир, 1975. 71 с.
19. Хантер Р. Проектирование и конструирование компиляторов. — М.: Финансы и статистика,
1984. 232 с.
20. Языки и автоматы: Сб. статей под ред. В.М.Курочкина. — М.: Мир, 1975. 358 с.
235
ИБН
Научная литература
Борис Константинович Мартыненко
Языки и трансляции
Учебное пособие
Редактор
Т.В. Мызникова
Компьютерная верстка Б.К. Мартыненко
236
