Мартыненко Б.К. Языки и трансляции

Подождите немного. Документ загружается.

180

Индукционный переход. Докажем, что тогда аналогичное утверждение

верно для

i = n +1.

Пусть

L ∈σ

’

n + 1

(A, B). Согласно шагу 2 алгоритма 2.6 либо L ∈σ

’

(A, B) и тогда в

соответствии с

индукционной гипотезой L∈σ

’

(A, B), либо существуют правило

A → X

…X

∈ P и L

’

∈σ

’(X

, B), X

∈V

, 1 ≤ p ≤ m, такие, что L = L

’

⊕

FIRST

p +1

p +2

…X

). Согласно индукционной гипотезе, примененной к

’

∈σ

’(X

, B), можем утверждать, что L

’

∈σ

’

, B) и что существует левосторон-

ний вывод вида

Bγ, а L

’

FIRST

(γ). Тогда можно построить

левосторонний вывод:

…X

p – 1

p + 1

…X

…w

p – 1

p + 1

…X

…w

p– 1

BγX

p + 1

…X

Согласно определению

FIRST

(γX

p + 1

… X

) ∈σ

’

( A, B). Кроме того,

FIRST

(γX

p +1

… X

FIRST

(γ) ⊕

FIRST

p +1

…X

) =

= L

’

⊕

FIRST

p +1

… X

) = L.

Итак,

L ∈σ

’

(A, B). Что и требовалось.

II. Покажем теперь, что

’

(A, B) ⊆ σ

’

(A, B).

Пусть

L∈σ

’

(A,B). Это значит, что существует левосторонний вывод A

wBα,

w ∈V

и L =

FIRST

(α). Индукцией по длине вывода l покажем, что L ∈σ

’

(A, B).

База. Пусть

l =1, т.е. A

wBα, w ∈V

и L =

FIRST

(α). Тогда существует

правило A → wBα и согласно шагу 1 алгоритма 2.6 L =

FIRST

(α) ∈σ

’

(A,B) ⊆

’

(A, B). База доказана.

Индукционная гипотеза. Предположим, что аналогичное утверждение

выполняется для всех

l ≤ n (n ≥ 1).

Индукционный переход. Докажем, что тогда аналогичное утверждение

верно для

l = n +1. Пусть

…X

p–1

p +1

…X

…w

p –1

p +1

…X

…w

p –1

BγX

p+1

…X

= wBα

— вывод длиной n +1, где w = w

…w

, X

→ w

Bγ∈P, α = γX

p+1

…X

, и

L =

FIRST

(α) =

FIRST

(γX

p +1

…X

) = L

’

⊕

FIRST

p +1

…X

где

’

FIRST

(γ). Именно благодаря этому обстоятельству L ∈σ

’

(A, B).

Одновременно согласно шагу 2 алгоритма

2.6 из существования вывода X

Bγ, l

≤ n, следует по определению, что L

’

FIRST

(γ) ∈σ

’

, B), а по ин-

181

дукционному

предположению, что σ

’

, B) ⊆σ

’

, B) и, следовательно, L

’

∈

’

, B). Кроме того, имеется правило A → X

…X

p + 1

…X

∈P. Согласно

шагу 2 алгоритма 2.6 L = L

’

⊕

FIRST

p + 1

…X

), где L

’

∈σ

’

, B) есть элемент

’

j + 1

(A, B). Но σ

’

j + 1

(A, B) = σ

’

(A, B). Итак, L ∈σ

’

(A, B).

Из рассуждений I и II следует равенство

’

(A, B) = σ

’

(A, B) и утверждение

теоремы.

§ 2.9. Алгоритм вычисления

функции

()

Сопоставляя определения функций

σ(A)={L ⊆ V

| ∃ S

wAα, w ∈V

, L =

FIRST

(α)}

()

= {w ∈V

| ∃ S

γAα и w ∈

FIRST

(α)}, A ∈V

нетрудно сообразить, что

()

∈

∪

Это равенство — ключ к модификации алгоритма вычисления

σ(A) , дающей

алгоритм вычисления

()

Алгоритм 2.7: вычисление

()

Вход: G = (V

, V

, P, S) — контекстно-свободная грамматика.

Выход:

()

для всех A ∈V

Метод.

Определим вспомогательную функцию

ϕ(A, B)={w ∈Σ

∃ A γBα, w ∈

FIRST

(α)}, где A, B ∈V

. Очевидно, что

()

= ϕ(S, A). Остается оп-

ределить алгоритм для вычисления функции

ϕ(A, B).

Вычисление значения

ϕ(A, B) производится по следующим шагам:

1. ϕ

(A, B)={ w ∈Σ

|∃ A →γBα∈P, α, γ∈V

, w =

FIRST

(α)}.

2. Пусть значения ϕ

(A, B), ϕ

(A, B),…, ϕ

(A, B) уже построены для всех

(A, B) ∈V

× V

. Тогда

i +1

(A, B)=ϕ

(A, B) ∪ {w ∈Σ

| ∃ A → X

…X

p +1

…X

∈P, X

∈V

w ∈ϕ

, B) ⊕

FIRST

p +1

… X

)}.

3. Шаг 2 повторяется до тех пор, пока при некотором i = j не окажется ϕ

j + 1

(A,

B)=ϕ

(A, B) для всех (A, B) ∈V

× V

. Такое j существует, ибо ϕ

(A, B) ⊆ ϕ

(A, B)

⊆…⊆ Σ

при том, что последнее множество является конечным. И тогда

ϕ(A, B)=ϕ

(A, B).

182

4. Полагаем

()

= ϕ(S, A) для всех A ∈V

\{S}и

()

S =

ϕ(S, S) ∪ {ε}, так как всегда ε∈

()

S , но может оказаться, что ε∉ϕ(S, S).

Пример 2.12. Пусть G = ({S, A}, {a, b}, P, S ), где P = {S → aAaa, S → bAba,

A → b, A → ε}.

Построим

множества

()

, используя описанный

алгоритм (табл. 2.6).

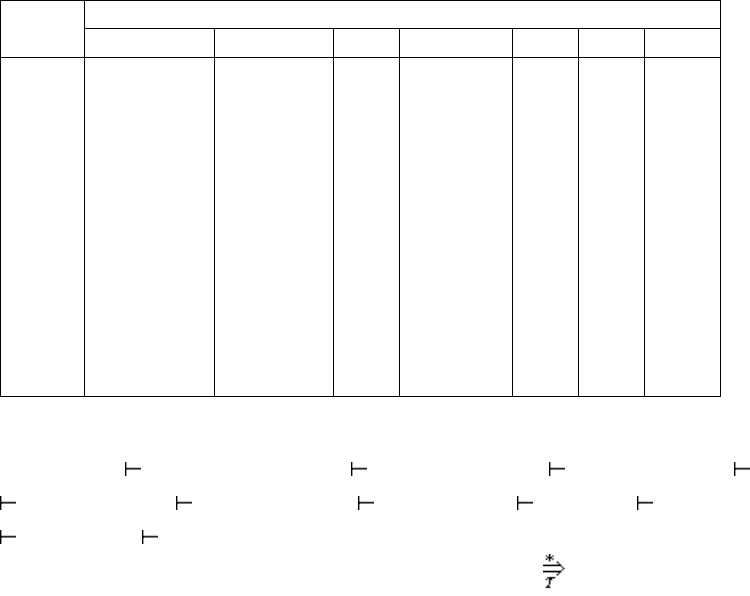
Табл. 2.6

Получаем

()

S = ϕ

(S, S) ∪ {ε}={ε};

()

A = ϕ

(S, A) = {aa, ba}.

Покажем теперь, что алгоритм 2.7 действительно вычисляет функцию

()

для любого нетерминала A.

Теорема 2.9. Пусть G = (V

, V

, P, S) — контекстно-свободная грамматика.

Алгоритм 2.7 правильно вычисляет функцию

()

для любого A

∈V

≥ 0.

Доказательство. Фактически достаточно показать, что

(A, B) = ϕ(A, B),

если

(A, B) = ϕ

(A, B) при i > j для всех A, B ∈V

I. Покажем сначала, что

(A, B) ⊆ϕ(A, B) или, что то же самое, если

∈ϕ

(A, B) при l ≤ j, то w ∈ϕ(A, B), используя индукцию по l.

База. Пусть l =0. Имеем w

∈ϕ

(A, B). Согласно шагу 1 алгоритма 2.7 суще-

ствует правило A

→γBα∈P, α, γ∈V

, и w∈

FIRST

(α). Это правило позволяет

построить вывод A

γBα, причем любая цепочка w ∈

FIRST

(α) также является

элементом множества

ϕ(A, B) — таково определение этой функции, т.е.

∈ϕ(A, B). База доказана.

Индукционная гипотеза. Предположим, что аналогичное утверждение

выполняется для всех l

≤ n (0 ≤ n ≤ j).

Индукционный переход. Докажем, что тогда аналогичное утверждение

верно для l = n +1.

Итак, пусть

w ∈ϕ

n +1

(A, B). Согласно шагу 2 алгоритма 2.7 либо w ∈ϕ

(A, B) и

тогда

согласно индукционной гипотезе w∈ϕ(A, B), либо существует правило

→ X

…X

p + 1

…X

∈P и w ∈ϕ

, B) ⊕

FIRST

p + 1

…X

), где X

∈V

N × N ϕ

(S, S)

∅ ∅

(S, A) {aa, ba} {aa, ba}

(A, S)

∅ ∅

(A, A)

∅ ∅

183

≤p ≤m. Иначе говоря, по определению операции ⊕

существуют w

∈ϕ

, B),

∈

FIRST

p +1

…X

) и w =

FIRST

). В соответствии с индукционным

предположением из того, что w

∈ϕ

, B), следует, что w

∈ϕ(X

, B). Это зна-

чит, что X

γBα и w

∈

FIRST

(α). Кроме того,

w =

FIRST

) =

FIRST

) ⊕

FIRST

) ⊆

⊆

FIRST

(α) ⊕

FIRST

p + 1

…X

) =

FIRST

(αX

p + 1

…X

)

и при этом существует вывод A

…X

p + 1

…X

…γBαX

p + 1

…X

Следовательно, w

∈ϕ(A, B).

II. Покажем теперь, что

ϕ(A, B) ⊆ϕ

(A, B). Пусть w ∈ϕ(A, B) благодаря то-

му, что существует вывод A

γBα и w ∈

FIRST

(α). Индукцией по длине вы-

вода l покажем, что w

∈ϕ

(A, B).

База. Пусть

l =1. Имеем A

γBα и w ∈

FIRST

(α). Тогда существует пра-

вило A

→

γBα∈P и согласно шагу 1 алгоритма 2.7 w ∈ϕ

(A, B) ⊆ϕ

(A, B). База

доказана.

Индукционная гипотеза. Предположим, что аналогичное утверждение

выполняется для всех l

≤ n (n ≥ 1).

Индукционный переход. Докажем, что тогда аналогичное утверждение

верно

для l = n +1. Пусть w ∈ϕ(A, B) благодаря тому, что существует вывод дли-

ной n +1

вида

…X

p –1

p +1

…X

δX

δβBχη = γBα,

в котором

…X

p –1

δ, X

p +1

…X

η, X

βBχ, α = χη, γ = δβ,

∈

FIRST

(α)=

FIRST

(χη)=

FIRST

(χ) ⊕

FIRST

(η) ⊆

⊆ϕ(X

, B) ⊕

FIRST

p +1

…X

) ⊆ϕ

, B) ⊕

FIRST

p +1

…X

) ⊆

⊆ϕ

j +1

(A, B)=ϕ

(A, B),

поскольку

FIRST

(χ) ⊆ϕ(X

, B) ⊆ϕ

, B). Последнее вложение следует в

соответствии с индукционной

гипотезой из существования вывода X

βBχ дли-

ной не больше n.

Здесь

использовано существование правила A → X

…X

p +1

…X

∈ P, бла-

годаря которому, учитывая шаг 2

алгоритма 2.7, мы заключили, что w∈ ϕ

j +1

( A,

B). Что и требовалось доказать.

Из рассуждений I и II следует равенство

(A, B)=ϕ(A, B) и утверждение

теоремы.

184

§ 2.10. k-Предсказывающий

алгоритм трансляции

Ранее в этой части пособия была доказана теорема 1.3 о том, что выходную

цепочку простой семантически однозначной трансляции можно сгенерировать

по левостороннему анализу входной цепочки посредством детерминированного

магазинного преобразователя. Если входная грамматика схемы синтаксически

управляемой трансляции принадлежит классу LL(k), то мы имеем детерминиро-

ванный механизм, правда, не преобразователь, а k-предсказывающий алгоритм

анализа, который выдает левосторонний анализ входной цепочки трансляции,

задаваемой такой схемой. Кроме того, в лемме

1.1 этой части был описан способ

построения недетерминированного магазинного преобразователя, реализующе-

го трансляцию, определяемую простой схемой. Использованный в ней прием

можно применить для модификации k-предсказывающего алгоритма анализа в

k-предсказывающий алгоритм трансляции, реализующий трансляцию, специфи-

цируемую простой семантически однозначной sdts с входной грамматикой

класса LL(k). Это устройство отличается от LL(k)-анализатора лишь тем, что

имеет еще один тип движений, состоящий в том, чтобы перенести верхний сим-

вол магазина, являющийся дубликатом выходного символа, на выходную ленту,

превратив его в настоящий выходной символ (как в лемме 1.1 этой части). Дета-

ли прояснятся из описания алгоритма 2.8.

Алгоритм 2.8: построение k-предсказывающего алгоритма трансляции.

Вход: T =(N,

Σ, ∆, R, S) — простая семантически однозначная схема

синтаксически управляемой трансляции с входной грамматикой G

класса LL(k).

Выход:

ℑ — k-предсказывающий алгоритм трансляции, реализующий транс-

ляцию

τ(T).

Метод.

1. Предполагая, что множество T LL(k)-таблиц, необходимых для анализа в

грамматике G

, уже построено, положим ℑ = (Σ, Γ∪{$}, ∆, M, X

, $), где Σ и ∆ —

такие же, как в схеме T; Γ = T ∪Σ∪∆

’

; ∆

’

={b

’

| b

’

= h(b), b ∈∆}; Σ∩∆

’

= ∅;

= T

S,{ε}

— начальный символ магазина; $ — маркер “дна” магазина; M:

(

Γ∪{$}) ×Σ

→ (Σ∪∆

’

)

∪ {pop, pass, accept, error} — управляющая таблица,

которая строится по следующим шагам:

2. M(T

A , L

, u)=x

’

, L

’

, L

’

, L

…T

, L

’

, если T

A, L

(u)=(A →

…A

, ·Y

, Y

, …, Y

Ò), и A → x

…A

...

…A

∈R — i-е правило схемы. Здесь y

’

= h(y

), i =0,1,2,…, m.

3. M(a, u) = pop, если a∈Σ, u = av, v ∈Σ

k–1

4. M(b

’

, u) = pass для всех u ∈Σ

. Такой управляющий элемент определяет

переход между конфигурациями: (x, b

’

α$, y) (x, α$, yb).

5. M($, ε) = accept.

6. M(X, u) = error для всех (X, u) ∈(Γ∪{$}) ×Σ

, для которых элементы M

не определены по пп. 2–5.

185

Пример 2.13. Пусть T =({S, A}, {a, b}, {a, b, e, ·, Ò}, R, S), где R = {(1) S →

aAaa, aAaa; (2) S

→ bAba, ·AÒa; (3) A → b, b; (4) A →ε, e}.

Входная грамматика этой схемы — не сильная LL(2)-грамматика, рассматри-

вавшаяся в предыдущих примерах. В примере 2.9 для нее был построен 2-

предсказывающий алгоритм анализа. Применяя алгоритм 2.8 к данной схеме,

получаем следующий 2-предсказывающий алгоритм трансляции, реализующий

определяемую ею трансляцию:

ℑ = ({a, b}, {T

, T

, a, b, a

’

, e, ·, Ò, $}, {a, b, e, ·, Ò}, M, T

, $),

где M представляется управляющей табл. 2.7.

Табл. 2.7

Аванцепочки

Маг.

сим-ы

aa ab ba bb a b

’

aaa

’

aaa

’

b·T

baÒa

’

a pop pop pop

b pop pop pop

’

pass pass pass pass pass pass pass

’

pass pass pass pass pass pass pass

e pass pass pass pass pass pass pass

pass pass pass pass pass pass pass

$ accept

Для иллюстрации работы только что построенного 2-предсказывающего

алгоритма трансляции рассмотрим обработку входной цепочки

bba:

(bba, T

$, ε) (bba, b·T

baÒa

’

$, ε) (ba, ·T

baÒa

’

$, ε) (ba, T

baÒa

’

$, ·)

(ba, ebaÒa

’

$, ·) (ba, baÒa

’

$, ·e) (a, aÒa

’

$, ·e) (ε, Ò$, ·e)

(ε, a

’

$, ·eÒ) (ε, $, ·eÒa).

Итак,

ℑ(bba)=<e>a. Нетрудно проверить, что (S, S) (bba, <e>a).

Замечание 2.2. Если входная грамматика схемы — LL(1)-грамматика или сильная

LL(k)-грамматика, то очевидно, что можно обойтись без построения LL(k)-таблиц, как

показано на следующем примере.

Пример 2.14. Пусть T = ({E, E

’

, T, T

’

, F}, {a, +,

, (, )}, {a, +,

}, R, E), где

R = { (1) E

→ TE

’

, TE

’

;

(5) T

’

→

’

;

(2) E

’

→ +TE

’

, T + E

’

; (6) T

’

→ ε, ε;

(3) E

’

→ ε, ε; (7) F → (E), E;

(4) T

→ FT

’

, FT

’

;

(8) F → a, a}.

186

Очевидно, что T — простая, семантически однозначная sdts с входной

грамматикой LL(1).

Посредством алгоритма 2.7 получаем следующий 1-

предсказы-вающий алгоритм трансляции:

ℑ = ({a,+,

,(, )}, {E, E

’

, T, T

’

, F, a, +,

, (, ), a’, +’,

’, $}, {a, +,

}, M, E, $),

где M представлена в табл. 2.8.

Табл. 2.8

Аванцепочки

Маг.

сим-ы

a +

∗

( )

’

E’

+T+’E’

ε ε

’

T’

’T

’

ε ε

aa’

(E)

a pop

+ pop

* pop

( pop

) pop

a’

’

pass

$ accept

Посмотрим, как будет действовать построенный нами 1-предсказывающий

алгоритм трансляции на входной цепочке (a+a)

((a+a),

E$, ε) ((a +a), TE

’

$, ε) ((a +a), FT

’

$, ε)

((a+a), (E) T

’

$, ε) (a +a), E) T

’

$, ε) (a +a), TE

’

) T

’

$, ε)

(a+a), F T

’

) T

’

$, ε) (a +a), aa’ T

’

) T

’

$, ε)

(+a), a

’

$, ε) (+a), T

’

) T

’

$, a) (+a), E

’

) T

’

$, a)

(+a), +T+’ E

’

) T

’

$, a) (a), T+’E

’

) T

’

$, a)

(a), FT

’

+’E

’

$, a) (a), aa’T

’

+’E

’

) T

’

$, a)

( ), a

’

+’E

’

) T

’

$, a) ( ), T

’

+’E

’

) T

’

$, aa)

( ), +’E

’

) T

’

$, aa) ( ), E

’

) T

’

$, aa+) (ε,T

’

$, aa+)

(ε, E

’

$, aa+) (ε, $, aa+).

Итак,

ℑ((a+a)) = aa+. Нетрудно проверить, что (E, E)

((a+a), aa+).

Не следует путать скобки, ограничивающие компоненты конфигурации, со скобками —

входными символами.

187

Теорема 2.10. Пусть T = (N, Σ, ∆, R, S) — простая семантически однознач-

ная

схема синтаксически управляемой трансляции с входной грамматикой G

класса LL(k) и ℑ = (Σ, Γ∪{$}, ∆, M, T

, $) — k-предсказывающий алгоритм

трансляции, построенный посредством алгоритма 2.7, примененного к данной

схеме трансляции T. Тогда

τ(T)=τ(ℑ).

Доказательство. Справедливость данного утверждения следует из того

факта, что LL(k)-анализатор, построенный по входной грамматике данной схе-

мы, является правильным. Модификация, превращающая его в LL(k)-трансля-

тор, фактически состоит в том, что когда анализатор, моделируя шаг левосто-

роннего вывода, замещает некоторую LL(k)-таблицу T

A, L

образом правой части

правила A → x

...A

вида x

…T

, транслятор “под-

мешивает” к этой магазинной цепочке выходные символы из семантической це-

почки соответствующего правила схемы таким образом, что полученная смесь

’

…T

’

в магазине обеспечивает точное воспроизведе-

ние движений анализатора и синхронизированную с ними генерацию соответст-

вующей цепочки на выходной ленте. Действительно, выполнив pop-движения

продвинувшись по фрагменту x

входной цепочки, который является также и

фрагментом правила входной грамматики A

→ x

...A

, транслятор тут же

выдает на выход соответствующий фрагмент y

выходной цепочки, который

также является и фрагментом семантической цепочки соответствующего прави-

ла схемы A

→ x

...A

, y

...A

Теорема 2.11. Пусть T = (N, Σ, ∆, R, S) — простая семантически однознач-

ная схема синтаксически управляемой трансляции

с входной грамматикой G

класса LL(k). Существует детерминированный магазинный преобразователь P,

такой, что

= {(x$, y) | (x, y) ∈τ(T)}.

Доказательство. Заметим, что входная цепочка трансляции, реализуемой

магазинным преобразователем, всегда имеет маркер конца, тогда как схема по-

рождает трансляцию с входами без такого маркера. Маркер необходим, чтобы

гарантировать детерминизм магазинного преобразователя.

Доказательство основано на построении dpdt, моделирующего движения k-

предсказывающего алгоритма трансляции, адекватного данной схеме, который

согласно теореме 2.6 существует.

Итак, пусть построен k-предсказывающий алгоритм трансляции

ℑ = (Σ, ∆, Γ∪{$}, M, T

, $).

Положим dpdt

P = (Q,

Σ ∪ {$}, Γ∪{$}, ∆, δ, q

, $, ∅),

где

Σ и Γ — те же, что и в ℑ; Q = {q

} ∪ {[u] | u ∈Σ

* k

} ∪ {[v$] | v ∈Σ

* k –1

188

1. δ(q

, ε, $) = ([ε], T

$, ε) — моделирует начальную конфигурацию ℑ.

2. δ([v], a, T ) = ([va], T, ε), v ∈Σ

* k –1

, a ∈Σ, T ∈T — накопление аванцепочки.

3. δ([v], $, T ) = ([v$], T, ε), v ∈Σ

* k –1

, T∈T — накопление короткой аванце-

почки.

4. δ([u], ε, T ) = ([u], β, ε), u ∈Σ

* k

, T∈T , M(T, u)=β — моделирование движе-

ния типа 1 .

5. δ([v$], ε, T ) = ([v$], β, ε), v ∈Σ

* k –1

, T∈T , M(T, v)=β — моделирование

движения типа 1 при короткой аванцепочке.

6. δ([av], ε, a) = ([v], ε, ε), a ∈Σ, v ∈Σ

* k –1

— моделирование pop-движения.

7. δ([av$], ε, a) = ([v$], ε, ε), a ∈Σ, v ∈Σ

* k –2

— моделирование pop-движения

при короткой аванцепочке.

8. δ([u], ε, b’) = ([u], ε, b), b ∈∆, v ∈Σ

* k

— моделирование pass-движения.

9. δ([v$], ε, b’) = ([v$], ε, b), b ∈∆, u ∈Σ

* k –1

— моделирование pass-движения

при короткой аванцепочке.

10. δ([$], ε, $) = ([ε], ε, ε) — моделирование перехода в принимающую

конфигурацию.

То, что построенный dpdt P действительно точно моделирует k-пред-

сказывающий алгоритм трансляции

ℑ, нетрудно доказать индукцией по числу

движений типа 1 того и другого устройств.

2.11. Непростые LL(k)-трансляции

и магазинные процессоры

Пусть T = (N, Σ, ∆, R, S) — непростая семантически однозначная sdts с вход-

ной грамматикой G

класса LL(k). Для реализации такой трансляции можно вве-

сти еще одну модификацию k-предсказывающего алгоритма анализа, называе-

мую магазинным процессором.

Магазинный процессор ведет анализ входной цепочки во входной граммати-

ке и генерирует дерево вывода выходной цепочки в выходной грамматике. Дру-

гими словами, он моделирует вывод элемента трансляции, используя магазин

для манипуляции над синтаксическими цепочками трансляционных форм, а се-

мантические цепочки этих форм представляет в виде дерева вывода в выходной

грамматике, разрастающегося в ходе вывода. В тот момент, когда в процессе

анализа он воспроизводит шаг замены крайнего левого нетерминала в синтакси-

ческой цепочке текущей трансляционной формы, происходит пристраивание

вершин, помеченных символами соответствующей семантической цепочки ис-

пользуемого правила схемы к вершине дерева вывода, представляющей связан-

ное вхождение одноименного нетерминала в семантической цепочке трансля-

ционной формы. Чтобы следить за связями между нетерминалами синтаксиче-

ской цепочки текущей трансляционной формы с соответствующими вершинами

дерева, представляющего семантические цепочки, используются указатели,

189

хранимые в магазине анализатора при нетерминалах или LL(k)-таблицах, ассо-

циированных с ними. Когда нетерминал (или LL(k)-таблица) на вершине мага-

зина подменяется цепочкой, представляющей синтаксический элемент правила

схемы, указатель, находящийся при нем (ней), указывает на вершину, к которой

надлежит пристроить новые вершины. Указатели же на эти вновь появившиеся

вершины помещаются в магазин при связанных вхождениях нетерминалов в

синтаксическом элементе правила, о котором шла речь.

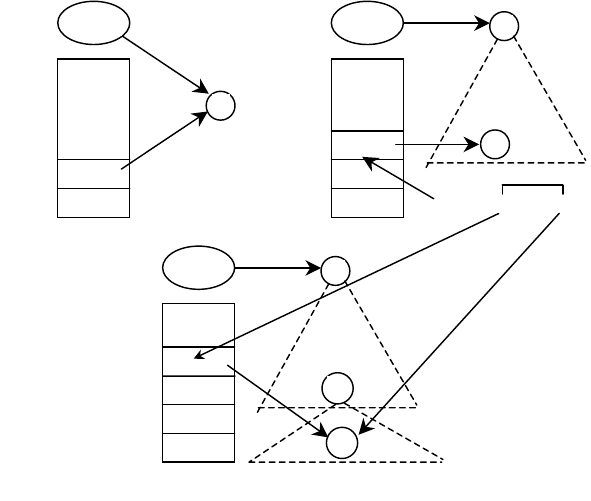
Проще всего проиллюстрировать работу магазинного процессора схемати-

чески — см. рис. 2.3).

На рис. 2.3, a представлена начальная конфигурация магазинного процес-

сора. В магазине кроме маркера “дна” магазина находится только начальная

LL(k)-таблица T

с указателем p

на корень строящегося дерева вывода в выход-

ной грамматике результата трансляции входной цепочки. Этот указатель запо-

минается также в отдельной переменной (Root), чтобы через него получить дос-

туп к дереву после его построения. На рис. 2.3, б представлена промежуточная

конфигурация магазинного процессора, когда часть дерева вывода построена.

Среди его листьев находится вершина, помеченная нетерминалом A. В рассмат-

риваемый момент на вершине магазина находится LL(k)-таблица T

A,L

с указате-

лем p

на вершину дерева вывода, к которой будет пристроено поддерево, пред-

ставляющее семантический элемент правила A

→ α

Bβ

, α

Bβ

, используемого

на этом шаге моделирования вывода. В правиле явно выделена пара связанных

вхождений одного нетерминала (B). Рис. 2.3, в иллюстрирует результат

Рис. 2.3.

, p

Root

, p

Root

A → α

, α

, q

Root