Мартыненко Б.К. Языки и трансляции

Подождите немного. Документ загружается.

160

Итак,

A(abbab) = 14232. Нетрудно проверить, что 14232 — действительно

левый анализ

abbab: достаточно лишь произвести левосторонний вывод с ис-

пользованием правил в указанной последовательности:

aBS abSBS abbBS abbaS abbab.

Следовательно,

A — правильный 1-предсказывающий алгоритм анализа для

грамматики

Пример 2.5. Построим детерминированный магазинный преобразователь,

моделирующий анализатор предыдущего примера. Поскольку грамматика была

простой, то нетрудно заметить, что за движением типа 1 сразу же следует pop-

движение, продвигающее анализатор к следующему символу входной цепочки

и стирающее верхний символ магазина, который всегда оказывается равным

входному. В отличие от анализатора dpdt будет продвигаться по входной цепоч-

ке при каждом движении. Соответственно в магазин он сразу будет писать пра-

вую часть правила без первого символа. Кроме того, конец входной цепочки бу-

дет маркирован, чтобы контролировать его достижение.

Принимая во внимание сказанное, положим

P = ({q

, q, accept}, {a, b, $}, {S, B, a, b, $}, {1, 2, 3, 4}, δ, q

, $, {accept}),

где

δ(q

, ε, $) = (q, S$, ε) — воспроизводит начальную конфигурацию A;

2) δ(q, a, S) = (q, BS, 1) — воспроизводит M(S, a) = (aBS, 1);

δ(q, b, S) = (q, ε, 2) — воспроизводит M(S, b) = (b, 2);

δ(q, a, B) = (q, ε, 3) — воспроизводит M(B, a) = (a, 3);

δ(q, b, B) = (q, SB, 4) — воспроизводит M(B, b) = (bSB, 4);

δ(q, $, $) = (accept, ε, ε) — сигнализирует о приеме.

Легко проверить, что (

w$, π) ∈τ

(P) тогда и только тогда, когда A(w)=π.

Посмотрим, как действует этот преобразователь на той же входной цепочке

abbab:

(

, abbab$, $, ε) (q, abbab$, S$, ε) (q, bbab$, BS$, 1) (q, bab$, SBS$, 14)

(q, ab$, BS$, 142) (q, b$, S$, 1423) (q, $, $, 14232) (accept, ε, ε, 14232).

Как видим, (

abbab$, 14232) ∈τ

(P).

§ 2.4. Построение

1-предсказывающего алгоритма анализа

по LL(1)-грамматике

Алгоритм 2.1: построение LL(1)-анализатора.

Вход: G =(V

, V

, P, S) — LL(1)-грамматика.

Выход: правильный A — 1-предсказывающий алгоритм анализа для грам-

матики

Метод. Положим A =(Σ, Γ∪{$}, ∆, M, X

, $), где Σ = V

, ∆ = {1, 2,…, #P},

Γ = V

∪ V

, X

= S.

161

Управляющая

таблица M определяется на множестве (Γ∪{$}) × (Σ∪{ε})

следующим образом:

M(A, a)=(α, i), если A → α является i-м правилом во множестве правил P,

a ∈

FIRST

(α), a ≠ε. Если ε∈

FIRST

(α), то M(A, b)=(α, i) для всех b ∈

(A);

M(a, a) = pop для всех a ∈Σ;

M($, ε) = accept;

M(X, a) = error для всех (X, a) ∈(Γ∪{$}) × (Σ∪{ε}), для которых значе-

ния элементов, остались не определенными по пп. 1–3.

Пример 2.6. Посредством алгоритма 2.1 построим LL(1)-анализатор для

LL(1)-грамматики G = ({E, E’, T, T’, F}, {a, +,

, (, )}, P, E), где

P = {(1) E → TE’, (2) E’→ +TE’, (3) E’→ ε, (4) T → FT’, (5) T’→

FT’,

(6) T’→ ε, (7) F → (E), (8) F → a}.

Положим

A = ({a, +,

, (, )}, {E, T, F, a, +,

, (, ), $}, {1, 2, 3, 4, 5, 6, 7, 8}, M,

E, $), где M дана в виде табл. 2.2. В ней пустые клетки соответствуют значениям

error.

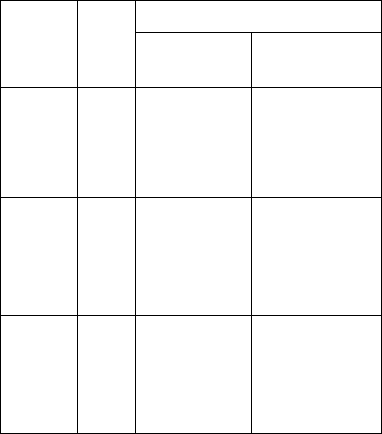
Табл. 2.2

Аванцепочки Маг.

сим-ы

a +

( )

’, 1

TE’, 1

E’

+TE

’

, 2

ε, 3 ε, 3

’, 4

FT’, 4

T’

ε, 6

’, 5

ε, 6 ε, 6

F a, 8 (E), 7

a pop

+ pop

pop

( pop

) pop

$ accept

1-Предсказывающий алгоритм анализа, использующий эту управляющую

таблицу, проанализировал бы входную цепочку (

a + a), совершив следующую

последовательность движений:

((

a + a), E$, ε) ((a + a), TE

’

$, 1) ((a + a), FT

’

$, 14)

((a + a), (E) T

’

$, 147) (a + a), E) T

’

$, 147) (a + a), TE

’

) T

’

$, 1471)

(a + a), F T

’

) T

’

$, 14714) (a + a), a T

’

) T

’

$, 147148)

162

(+ a), T

’

) T

’

$, 147148) (+ a), E

’

) T

’

$, 1471486)

(+ a),+TE

’

) T

’

$, 14714862) (a), TE

’

) T

’

$, 14714862)

(a), F T

’

) T

’

$, 147148624) (a), a T

’

) T

’

$, 1471486248)

( ), T

’

$, 1471486248) ( ), E

’

) T

’

$, 14714862486)

( ), ) T

’

$, 147148624863) (ε,T

’

$, 147148624863)

(ε, E

’

$, 1471486248636) (ε, $, 14714862486363).

Итак,

A((a + a)) = 14714862486363. Нетрудно проверить, что E

(

a + a), где

π = 14714862486363.

Теорема 2.4. Алгоритм 2.1 производит правильный 1-предсказывающий ал-

горитм анализа для любой LL(1)-грамматики.

Доказательство. Пусть

G =(V

, V

, P, S) — LL(1)-грамматика, и A — 1-

предсказывающий

алгоритм анализа для грамматики G, построенный согласно

алгоритму 2.1. Требуется доказать, что S

x тогда и только тогда, когда

(x, S$, ε) (ε, $, π).

По индукции докажем вспомогательное утверждение, общий смысл которо-

го состоит в том, что анализатор в своем магазине воспроизводит последова-

тельность открытых частей сентенциальных форм левостороннего вывода вход-

ной цепочки, если она выводима в данной грамматике

G, причем если π — по-

следовательность номеров правил, участвующих в ее выводе, то

π образуется на

выходе анализатора.

Докажем сначала, что если S

xα, где x ∈Σ

— закрытая часть, а α∈

(

∪ V

)

— открытая часть данной сентенциальной формы, то для любой це-

почки

y∈Σ

, такой, что

FIRST

(

y) ∈

FIRST

(α), анализатор совершает переход

(xy, S$, ε) (y, α$, π).

Индукция по

l = |π|.

База. Пусть

l =1, т.е. π = i, где i — номер некоторого правила грамматики.

Пусть

xα и y ∈Σ

— такая цепочка, что

FIRST

(

y) ∈

FIRST

(α). На един-

ственном шаге этого вывода применялось правило вида

S → xα, имеющее номер

i. Для всех a ∈

FIRST

(xα

(S)) согласно алгоритму 2.1 M(S, a)= (xα, i)

Посмотрим, как будет действовать анализатор, начиная с конфигурации

(

xy, S$, ε). Очевидно, что аванцепочка

u =

FIRST

(

xy) ∈

FIRST

(xα)=

FIRST

(xαε) ⊆

FIRST

(xα

(S))

и, следовательно, M(S, u)=(xα, i). Поэтому (xy, S$, ε) (xy, xα$, i) (y, α$, ε),

причем последний переход реализуется посредством pop-движений. База дока-

зана.

163

Индукционная

гипотеза. Предположим, что утверждение выполняется

для всех

l ≤ n (n ≥ 1).

Индукционный переход. Докажем утверждение для

l= n +1. Пусть име-

ется левосторонний вывод длиной

n +1: S

x’α’= x’Aγ

x’βγ = xα. Здесь

π = π’i, α’= Aγ, βγ = zα, где z ∈V

, x = x’z, A∈V

, β, γ∈V

. На последнем шаге

вывода применялось правило

A →β — i-е правило из множества правил P. Со-

гласно алгоритму

2.1

M(A , a)=(β, i) для всех a ∈

FIRST

(β

(A )). (2.1)

Посмотрим, как будет действовать анализатор из своей начальной конфигу-

рации (

xy, S$, ε)=(x’zy, S$, ε) = (x’y’, S$, ε), где y’= zy.

Применим к имеющемуся выводу

x’α’ индукционную гипотезу с цепоч-

кой

y’, поскольку

FIRST

(

y’) =

FIRST

(

zy) ∈

FIRST

(zα) =

FIRST

(βγ) ⊆

FIRST

(Aγ)=

FIRST

(α’).

Как следствие получаем

(xy, S$, ε) = (x’zy, S$, ε) = (x’y’, S$, ε) (y’, α’$, π’)=(zy, Aγ$, π’).

Вычислим аванцепочку от

zy:

u =

FIRST

(

zy) ∈

FIRST

(zα) =

FIRST

(βγ) ⊆

FIRST

(β

(A )),

для таких аванцепочек, как показывает (2.1), M(A, u) = (β, i). Поэтому следу-

ющее движение и завершающие pop-движения продолжают процесс таким об-

разом:

(zy, Aγ$, π’) (zy, βγ$, π’i) = (zy, zα$, π’i) (y, α$, π).

Что и требовалось.

II.

Докажем теперь, что если анализатор совершает переход вида (xy, S$, ε)

(

y, α$, π) для любой цепочки y ∈Σ

, такой, что

FIRST

(

y) ∈

FIRST

(α), то S

xα, где x — закрытая часть, а α — открытая часть данной сентенциальной фор-

мы.

Индукция по

l = |π|.

База. Пусть

l =1, т.е. π = i.

Имеем (

xy, S$, ε) (y, α$, i). Анализатор пишет на выходную ленту номер

правила только при движении типа 1, а оно совершается только при наличии

нетерминала на вершине магазина. Следовательно, это — первое движение, и

только оно пишет номер

i на выход. Поэтому фактически имеем

(

xy, S$, ε) (xy, β$, ε) (y, α$, i),

164

причем все остальные движения — это pop-движения. Очевидно, что только при

β = xα достижима завершающая конфигурация. Первое движение обеспечивает-

ся элементом таблицы

M(S, a)=(β, i), где u =

FIRST

(

xy), а это подразумевает

существование правила

S → β = xα под номером i. Чтобы первое движение

могло произойти, необходимо, чтобы

u ∈

FIRST

(xα

(S)). И это дей-

ствительно так, поскольку

u =

FIRST

(

xy) ∈

FIRST

(xαε) ⊆

FIRST

(xα

(S)).

А тогда

xα.

Индукционная гипотеза. Предположим, что утверждение выполняется

для всех l

≤ n (n ≥ 1).

Индукционный переход. Докажем утверждение для

l = n +1.

Пусть

(xy, S$, ε)=(x’y’, S$, ε) (y’, α’$, π’)=(y’, Aγ$, π’) ( y’, βγ$, π’i)

(y, α$, π),

где

π = π’i, |π’| = n, xy = x’y’, α’= Aγ. Завершающие pop-движения показывают,

что y’= zy, βγ = zα; т.к. xy = x’y’ = x’zy, то x = x’z.

Последнее движение типа 1 было выполнено благодаря элементу M(A, u’)=

(

β, i) для u’∈

FIRST

(

y’), что предполагает существование правила A →β под но-

мером

i, а также выполнение условия u’∈

FIRST

(β

(A)). Оно дейст-

вительно выполняется, поскольку

u’∈

FIRST

(

y’) =

FIRST

(

zy) ∈

FIRST

(zα) =

FIRST

(βγ) ⊆

FIRST

(β

(A)).

Одновременно можно воспользоваться индукционной гипотезой в применении

к (

x’y’, S$, ε) (y’, α’$, π’), поскольку

FIRST

(

y’) =

FIRST

(

zy) ∈

FIRST

(zα) =

FIRST

(βγ) ⊆

FIRST

(Aγ)=

FIRST

(α’),

получить как следствие S

x’α’ = x’Aγ

x’βγ = x’zα = xα. Что и требовалось.

Из утверждений I и II при

y = α = ε заключаем, что S

x тогда и только то-

гда, когда (

x, S$, ε) (ε, $, π). А это и означает, что 1-предсказывающий алго-

ритм анализа, построенный согласно алгоритму 2.1, является правильным для

LL(1)-грамматики G. Теорема доказана.

Замечание 2.1. Алгоритм 2.1 пригоден для построения анализаторов для LL(k)-

грамматик и при k >1, если только они сильные. При его применении к сильным LL(k)-

грамматикам всюду, где используется параметр 1, следует использовать значение k.

165

Прежде чем перейти к обсуждению

LL-анализа при k > 1, введем в рас-

смотрение еще одну полезную операцию над языками.

Определение 2.10. Пусть Σ — некоторый алфавит и L

, L

— подмножества

. Положим

Пример 2.7. Пусть L

= {ε, abb} и L

= {b, bab}. Тогда L

⊕

= {b, ba, ab}.

Операция

⊕

подобна инфиксной операции

FIRST

Лемма 2.1. Для любой контекстно-свободной грамматики G=(V

, V

,P, S) и

любых цепочек α,β∈V

имеет место тождество

FIRST

(αβ) =

FIRST

(α) ⊕

k FIRST

(β).

Доказательство.

Пусть w ∈

FIRST

(αβ). Докажем, что тогда w ∈

FIRST

(α) ⊕

FIRST

(β).

Обозначим

FIRST

(α), L

FIRST

(β). Из того, что w ∈

FIRST

(αβ),

следует,

что w =

FIRST

(uv), если α u, β v. Последние два вывода означают,

что x =

FIRST

(u) ∈

FIRST

(α)=L

Аналогично y =

FIRST

(v) ∈

FIRST

(β)=L

. Учитывая определение

опера-

ции

⊕

заключаем, что

FIRST

(xy) ∈L

⊕

Остается убедиться в том, что

FIRST

(xy) =

FIRST

(uv) = w. Так как x =

FIRST

(u), а y =

FIRST

(v), то u = xu’ и v = yv’ при некоторых u’, v’∈V

, при-

чем если

|x| < k, то u’= ε, и если |y | < k, то v’ = ε. Итак, имеем uv = xu’yv’.

Если

|x| = k, то w=

FIRST

(uv)=x =

FIRST

(xy). Если |x| < k, то u’= ε и

w =

FIRST

(uv)=

FIRST

(xyv’), причем, если |y | < k, то v’= ε и тогда w=

FIRST

(uv)=

FIRST

(xy), если же |y | = k, то

FIRST

(uv)=

FIRST

(xyv’)=

FIRST

(xy). Итак,

w =

FIRST

(uv)=

FIRST

(xy) ∈L

⊕

FIRST

(α) ⊕

FIRST

(β).

II.

Пусть w ∈

FIRST

(α) ⊕

FIRST

(β). Докажем, что тогда w∈

FIRST

(αβ).

Согласно определению операции

⊕

существуют цепочки x ∈

FIRST

(α),

y ∈

FIRST

(β) и w =

FIRST

(xy). Кроме того, согласно определению

FIRST

имеем α xu, β yv при некоторых u, v ∈V

FIRST

(xuyv) ∈

FIRST

(αβ).

Остается убедиться в том, что

FIRST

(xuyv)=

FIRST

(xy).

⊕

w ∈Σ

x ∈L

, y ∈L

, w =

y, если

≤ k,

FIRST

(xy) в противном случае

166

Если

|x | = k, то

FIRST

(xuyv)=

FIRST

(xy)=x. Если |x | < k, то u = ε и

FIRST

(xuyv)=

FIRST

(xyv), причем, если |y | < k, то v = ε и

FIRST

(xuyv)=

FIRST

(xy), в противном случае от v ничего не зависит и

FIRST

(xuyv)=

FIRST

(xy). Следовательно, w =

FIRST

(xy) =

FIRST

(xuyv)∈

FIRST

(αβ).

Из рассуждений I и II следует утверждение леммы. Что и требовалось.

§ 2.5. Анализ

в LL(k)-грамматиках

В общем случае анализа в LL(k)-грамматиках по нетерминалу и аванцепочке

невозможно однозначно определить правило для построения очередной

сентенциальной формы. Рассмотрим, например,

LL(2)-грамматику из примера

2.3:

S → aAaa | bAba; A → b | ε.

Согласно

алгоритму 2.1 для замены нетерминала A в выводе S

wAα wx

следует применять правило A → β, если аванцепочка u =

FIRST

(x) принадле-

жит множеству

FIRST

(β

(A)). Очевидно, что в нашем примере

(A) = {aa, ba}. Получается так, что следует применять правило A → b,

если аванцепочка из

FIRST

(A )) =

FIRST

(b{aa, ba}) = {ba, bb},

или правило

A → ε, если аванцепочка из множества

FIRST

(ε

(A )) =

{

aa, ba}. Соображения о том, как определять, какое правило из этих двух ис-

пользовать для замены нетерминала

A, если аванцепочка равна ba, уже были

рассмотрены в упомянутом примере. Эту неопределенность можно разрешить,

если для определения правила, по которому следует раскрывать нетерминал,

помимо нетерминала и аванцепочки использовать еще один параметр:

A,L

—

так называемую

LL(k)-таблицу

, ассоциированную с двумя индексами, первый

из которых — нетерминал

A, второй — множество L, вычисляемое с учетом

следующих рассуждений.

Пусть имеется вывод

wAα в некоторой LL(k)-грамматике. Вспоминая

теорему 2.1, нетрудно сообразить, что критерием выбора правила

A → β для

продолжения этого вывода может служить факт принадлежности текущей аван-

цепочки множеству

FIRST

(βα)=

FIRST

(β) ⊕

FIRST

(α)=

FIRST

(β) ⊕

где

L =

FIRST

(α). Это множество L и есть тот второй индекс таблицы T

A, L

, о

котором шла речь. По аванцепочке таблица

A,L

выдает правило, которое следует

использовать для замены нетерминала

A в текущей левосентенциальной форме.

Не путать с управляющей таблицей k-предсказывающего алгоритма анализа.

167

Ясно, что для любой cfg число таких

LL(k)-таблиц конечно и все таблицы,

необходимые для анализа в данной грамматике, могут быть построены

заблаговременно. Они используются

k-предсказывающим алгоритмом анализа в

магазинных цепочках взамен нетерминалов (см. алгоритм 2.2 далее).

Теперь дадим точное определение

LL(k)-таблиц и опишем способ построе-

ния множества

LL(k)-таблиц, необходимых для анализа в данной LL(k)-грам-

матике.

Определение 2.11. Пусть G =(V

, V

, P, S) — контекстно-свободная грамма-

тика. Для каждого

A ∈V

и L ⊆ V

определим T

A, L

— LL(k)-таблицу, ассоции-

рованную с

A и L как функцию, которая по данной аванцепочке u ∈V

выдает

либо значение error, либо

A-правило

и конечный список подмножеств V

Именно:

A, L

(u) = error, если не существует ни одного правила вида A →α∈P, та-

кого, что

u ∈

FIRST

(α) ⊕

A, L

(u)=(A →α, ·Y

, Y

,…, Y

Ò), если A →α — единственное правило из

P, такое, что u ∈

FIRST

(α) ⊕

L; при этом, если α = x

…B

, B

∈V

, то Y

FIRST

i + 1

…B

) ⊕

L, i =1,2,…,m; j = 0,1,…,m; m ≥ 0;

A,L

(u) = undefined, если существует несколько A-правил: A →α

| α

|…|α

таких, что

u ∈

FIRST

(α

) ⊕

L для 1 ≤ i ≤ n, n ≥ 2.

Множество терминальных цепочек

называется множеством локальных

правых контекстов для B

. В частности, если m =0, то T

A,L

(u) = (A → α, ∅).

Случай 3 для

LL(k)-грамматик не актуален.

Пусть мы имеем левосторонний вывод в

LL(k)-грамматике: S

wAγ

wx.

Как

было сказано в начале этого параграфа, именно таблица T

A,L

, где L =

FIRST

(γ), сообщит, что следующую за wAγ сентенциальную форму следует по-

лучать при помощи правила A → α, если для u =

FIRST

(x) окажется, что T

A, L

(u) =

(

A → α, ·Y

,…, Y

Ò). Если α = x

…B

, то следующая за wAγ сентенци-

альная форма будет

wαγ = wx

…B

γ, и в свое время раскрытием B

будет

руководить

LL(k)-таблица T

, а раскрытием B

— LL(k)-таблица T

Пример 2.8. Рассмотрим уже не раз обсуждавшуюся LL(2)-грамматику с

правилами

S → aAaa | bAba; A → b | ε и построим все LL(2)-таблицы, необхо-

димые для анализа в этой грамматике.

Начнем с таблицы

S,{ε}

: именно она диктует выбор первого правила для рас-

крытия нетерминала

S. Используя правило S → aAaa, вычисляем

FIRST

(aAaa)

⊕

{ε} = {ab, aa}. Используя правило S → bAba, вычисляем

FIRST

(bAba) ⊕

{ε} = {bb}. Соответственно определяем LL(2)-таблицу: T

= T

S,{ε}

(табл. 2.3).

A-Правило — правило cfg с нетерминалом A в левой части.

168

Табл. 2.3

T(u)

LL(2)-

табл.

Правило

Мн-во лок.

прав. конт-в

= T

, {ε}

S → aAaa

S → bAba

·{ aa }Ò

·{ ba }Ò

= T

{aa}

A → b

A → ε

—

= T

{ba}

A → b

A → ε

—

Глядя на T

, легко определить, что потребуются еще таблицы T

= T

A ,{aa}

и T

A ,{ba}

. Таблица T

получается с учетом того, что для правила A → b получаем

FIRST

(b) ⊕

{aa}={ba}, а для правила A →ε —

FIRST

(ε) ⊕

{aa}={аa}.

Таблица

получается с учетом того, что для правила A → b имеем

FIRST

(b) ⊕

{ba} = {bb}, а для правила A →ε —

FIRST

(ε) ⊕

{ba}={ba}. В

правых частях правил для нетерминала

A нет ни одного нетерминала. Поэтому в

двух последних таблицах множества локальных правых контекстов пусты.

При построении этих

LL(2)-таблиц мы придерживались простой дисципли-

ны: начинали с построения начальной таблицы

S,{ε}

, а затем в каждой из уже

построенных

LL(2)-таблиц использовали значения элементов, чтобы определить

пары индексов других необходимых таблиц — каждое вхождение нетерминала в

правило сочеталось с соответствующим локальным множеством. Этот порядок

построения

LL(k)-таблиц фиксируется в следующем описании алгоритма:

Алгоритм 2.2: построение множества LL(k)-таблиц, необходимых для ана-

лиза в данной

LL(k)-грамматике.

Вход: G =(V

, V

, P, S) — LL(k)-грамматика.

Выход: T — множество LL(k)-таблиц, необходимых для анализа в грамматике G.

Метод.

1. Построить T

= T

S, {ε}

и T ={T

2. Если T

A, L

∈T и для некоторой цепочки u ∈V

и T

A,L

(u)=(A → x

…

, ·Y

, Y

,…, Y

Ò), то к множеству таблиц T добавить те таблицы из множест-

ва

| i =1, 2,…, m}, которых нет в T.

3. Повторять шаг 2 до тех пор, пока ни одну новую LL(k)-таблицу не удастся

добавить к

169

Такой момент обязательно настанет, так как для любой данной cfg

G суще-

ствует только конечное число таких таблиц (число нетерминалов — конечно,

число подмножеств

L ⊆ V

тоже конечно). Фактически же для анализа требу-

ются не все возможные

LL(k)-таблицы, которые можно построить для грамма-

тики

G, а только те, которые определяются описанным алгоритмом.

Алгоритм 2.3: построение k-предсказывающего алгоритма анализа.

Вход: G =(V

, V

, P, S) — LL(k)-грамматика.

Выход: A — правильный k-предсказывающий алгоритм анализа для G.

Метод.

1. Построим T — множество необходимых LL(k)-таблиц для грамматики G.

2. Положим A =(Σ, Γ∪{$}, ∆, M, T

, $), где Σ = V

, ∆ = {1, 2,…, #P}, Γ =

T ∪ V

, где T

= T

S,{ε}

3. Управляющую таблицу M определим на множестве (Γ∪{$}) ×Σ

сле-

дующим образом:

3.1.

M(T

A, L

, u) = (x

, Y

…T

, Y

, i), если T

A, L

(u) = (A → x

…

, ·Y

, Y

,…, Y

Ò), и A → x

…B

является i-м правилом в P.

3.2.

M(a, av) = pop для всех a ∈Σ, v ∈Σ

3.3.

M($, ε) = accept.

3.4.

M(X, u) = error для всех (X, u) ∈(Γ∪{$}) ×Σ

, для которых значения

элементов, остались не определенными по пп. 1–3.

Пример 2.9. Рассмотрим еще раз LL(2)-грамматику, обсуждавшуюся в

примере 2.3, с правилами

S → aAaa, 2) S → bAba, 3) A → b, 4) A → ε.

Используя уже построенные для нее

LL(2)-таблицы легко собрать управляющую

таблицу для этой грамматики — см. табл. 2.4.

Табл. 2.4

Аванцепочки Маг.

сим-ы

aa ab ba bb a b

aa, 1 aT

aa, 1 bT

ba, 2

ε, 4

b, 3

ε, 4

b, 3

a pop pop pop

b pop pop pop

$ accept

Например, на входной цепочке bba этот 2-предсказывающий алгоритм ана-

лиза проходит следующие конфигурации:

(

bba, T

$, ε) (bba, bT

ba$, 2) (ba, T

ba$, 1) (ba, ba$, 24)

(a, a$, 24) (ε, $, 24).

В то же время, посредством правил 1 и 2, получаем

bAba

bba.