Мартыненко Б.К. Языки и трансляции

Подождите немного. Документ загружается.

200

Пример 3.6. Обратимся еще раз к грамматике из примера 3.1. Как мы уви-

дим далее, она —

LR(1)-грамматика. Она имеет следующие правила: 1) S →

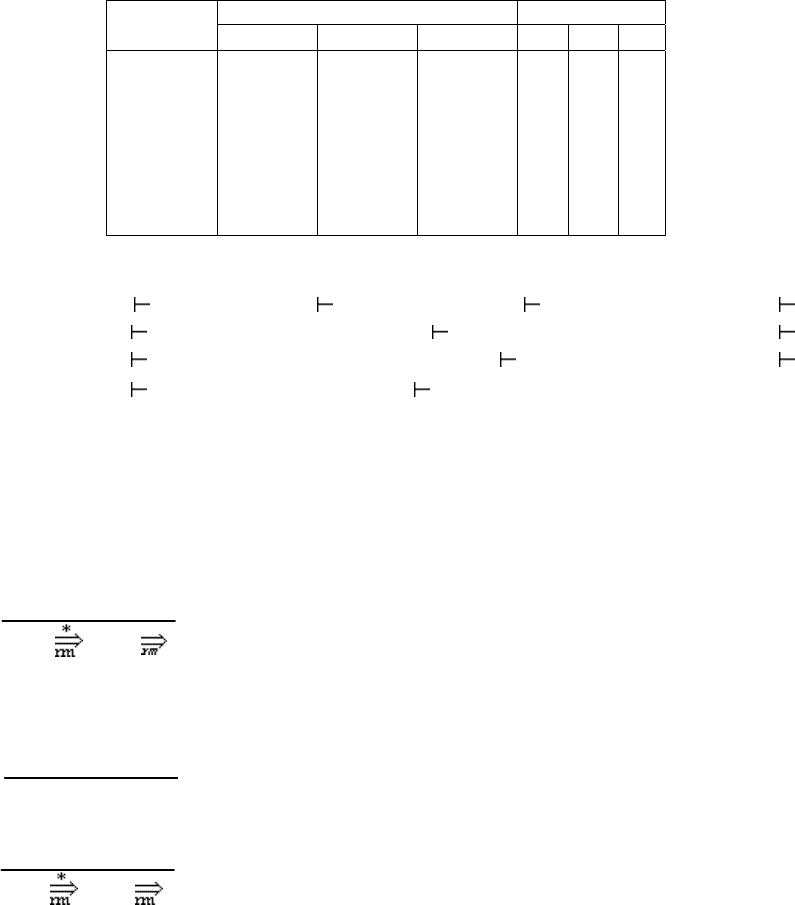
SaSb, 2) S → ε. Управляющая таблица LR(1)-анализатора, построенная для нее,

имеет вид, представленный табл. 3.3, где пустые клетки соответствуют значени-

ям error.

Табл. 3.3

f(u) g(X)

LR(1)-

таблицы

a b

S a b

reduce 2

reduce 2 T

shift

reduce 2 reduce 2 T

shift shift T

reduce 2 reduce 2 T

reduce 1 reduce 1

shift shift T

reduce 1 reduce 1

Рассмотрим действия этого анализатора на входной цепочке aabb:

(

, aabb, ε) (T

, aabb, 2) (T

, abb, 2) (T

, abb, 22)

, bb, 22) (T

, bb, 222)

, b, 222) (T

, b, 2221)

, ε, 2221) (T

, ε, 22211).

Итак, цепочка

aabb принимается, и π

= 22211 — ее правосторонний анализ.

§ 3.4. Свойства

LR(k)-грамматик

Рассмотрим некоторые следствия из определения LR(k)-грамматик, подво-

дящие нас к механизму анализа.

Определение 3.4. Пусть G = (V

, V

, P, S) — контекстно-свободная грамма-

тика и

αAw

αβw — некоторый правосторонний вывод в грамматике G,

где

α,β∈(V

∪V

)

, w ∈V

Активным префиксом сентенциальной формы αβw называется любая началь-

ная часть (префикс) цепочки

αβ, включая, в частности, ε и всю эту цепочку.

Определение 3.5. Пусть G = (V

, V

, P, S) — контекстно-свободная грам-

матика и

A →β

∈P. Композицию [A → β

.β

, u], где u ∈V

, назовем

LR(k)-ситуацией.

Определение 3.6. Пусть G = (V

, V

, P, S) — контекстно-свободная грамма-

тика

и S

αAw

αβw — правосторонний вывод в грамматике G, где β = β

,β

∈(V

∪V

)

. Назовем [A →β

.β

, u], где u =

FIRST

(w), LR(k)-ситуацией,

допустимой для активного префикса αβ

201

Пример 3.7. Обратимся еще раз к LR(0)-грамматике из примера 3.3, кото-

рая содержит следующие правила:

S → C | D, 2) C → aC | b, 3) D → aD | c.

Рассмотрим правосторонний вывод

S C. В сентенциальной форме C ос-

новой является

C. Эта форма имеет два активных префикса: ε и C. Для активно-

го префикса

ε допустима LR(0)-ситуация [S → .C, ε], а для активного префикса

C — LR(0)-ситуация [S → C., ε].

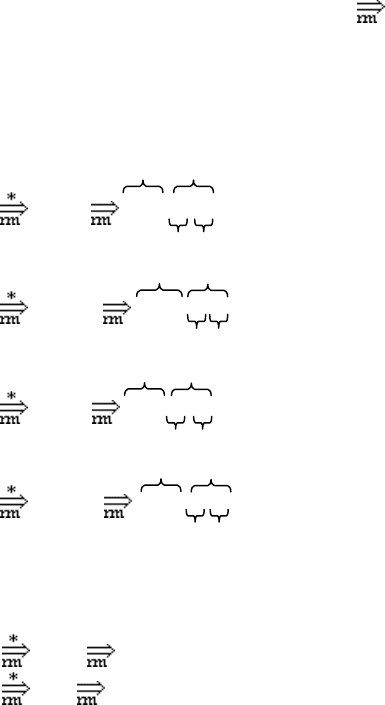
Рассмотрим выводы, дающие активный префикс

aaaa, и LR(0)-ситуации, до-

пустимые для него:

aaaC

aaa a C , αβ

= aaaa, [C → a.C, ε];

aaaaC

aaaa b , αβ

= aaaa, [C → .b, ε];

aaaD

aaa a D , αβ

= aaaa, [D → a.D, ε];

aaaaD

aaaa c , αβ

= aaaa, [D → .c, ε].

Во всех случаях правый контекст основы пуст.

Лемма 3.2. Пусть G = (V

, V

, P, S) — не LR(k)-грамматика. Тогда сущест-

вуют два правосторонних вывода в пополненной грамматике:

’

αAw

αβw;

’

γBx

γδx = αβy, такие, что x, y, w ∈V

а)

FIRST

(w) =

FIRST

( y),

б)

γBx ≠ αAy,

в)

|γδ| ≥ |αβ|.

Доказательство. Если

G — не LR(k)-грамматика, то условия а) и б) выпол-

няются как прямое следствие из определения

LR(k)-грамматик. Условие в) не-

формально означает, что правая граница основы в последней сентенциальной

форме второго вывода удалена от ее начала, по крайней мере, не менее, чем

удалена основа в последней сентенциальной форме в первом выводе. Это усло-

вие не столь очевидно. Простой обмен ролями этих двух выводов ничего не да-

ет, так как этим приемом мы добъемся только выполнения условий а) и в), но не

очевидно, что при этом будет выполнено условие б).

202

Предположим, что выводы 1 и 2 удовлетворяют условиям а) и б), но условие

в) не выполнено, т.е. что

|γδ|< |αβ|. Покажем, что тогда найдется другая пара

выводов, которые удовлетворяют всем трем условиям.

Поскольку

γδx = αβy, то |γδx| = |αβy|, и, учитывая, что |γδ|< |αβ|, заключа-

ем:

|x | > |y |, т.е. x = zy при некотором z ∈V

, |z | >0. Заметим, что цепочка z яв-

ляется префиксом цепочки

x, а не ее окончанием, так как именно цепочка y яв-

ляется окончанием всей сентенциальной формы

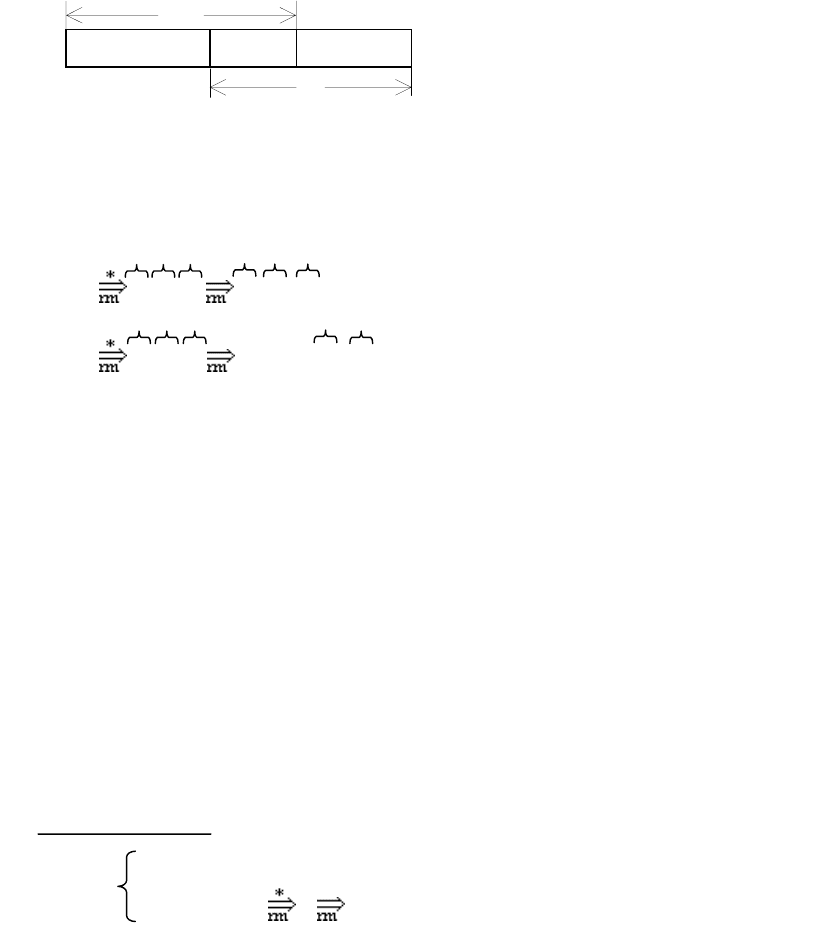
αβy. Два разных разбиения од-

ной и той же сентенциальной формы

γδx = αβy представлено на рис. 3.2.

Условие

γδx = αβy можно переписать как γδzy = αβy, и потому

γδz = αβ. (3.1)

Второй вывод разметим по образцу первого с учетом равенства

x = zy, а пер-

вый разметим по образцу второго с учетом равенства (3.1):

’

) S

’

γ B zy

γ δ zy ,

’

) S

’

α A w

αβw = γδ zw .

Эти два вывода обладают следующими особенностями:

’)

FIRST

([w]) =

FIRST

([y]), так как [w]=zy, [y]=zw и

FIRST

(w)=

FIRST

( y);

’) [γ][B][x] ≠ [α][A][y], так как [γ]=α, [B]=A, [x]=w, [α]=γ, [A]=B, [y]=zw, по-

скольку [

γ][B][x]=αAw и [α][A][y]=γBzw, а цепочки αAw и γBzw не могут быть

равными, так как их терминальные окончания

w и zw не равны между собой,

ибо

|z |>0.

Наконец, выполняется условие

’) |[γδ]| > |[αβ]|, ибо [γδ] = αβ, [αβ] = γδ и |γδ| < |αβ| по предположению.

Итак, исходная пара правосторонних выводов 1 и 2, которые обменялись ро-

лями, представлены в требуемом виде 1

’

и 2

’

, которые удовлетворяют всем трем

условиям а

’), б

’

) и в

’

). Что и требовалось доказать.

Введем функцию

EFF

(α), где α∈(V

∪V

)

, необходимую для построения

LR(k)-анализатора. Она будет помогать при определении, является ли ε-це-почка

основой для данной сентенциальной формы, подлежащей свертке.

Определение 3.7. Пусть G = (V

, V

, P, S) — cfg и α∈(V

∪V

)

. Положим

[

]

[B] [x]

[α

]

[y]

[α]

[A]

[w]

[α]

[

]

[w]

EFF

(α) =

FIRST

(α), если α начинается на терминал, а иначе

{w∈V

|∃α

wx, где β≠Awx, A∈V

, |w|= k или |w|< k и x = ε}.

γδ

αβ

Рис. 3.2.

203

Говоря неформально, функция

EFF

(α) ничем не отличается от функции

FIRST

(α), если α начинается с терминала, а если α начинается с нетерминала,

то при правостороннем выводе именно он является последним нетерминалом,

который замещается терминальной цепочкой на последнем шаге вывода. Функ-

ция

EFF

отличается от функции

FIRST

тем, что

в первую не включаются

префиксы терминальных цепочек, если эти цепочки получены посредством

ε-

правила, примененного на последнем шаге вывода.

Пример 3.8. Рассмотрим контекстно-свободную грамматику со следующи-

ми правилами:

S → AB, 2) A → Ba | ε, 3) B → Cb | C, 4) C → c | ε.

Вычислим функцию

EFF

(S). Поскольку аргумент начинается на нетерми-

нал, то согласно определению 3.7 необходимо построить всевозможные право-

сторонние выводы, начинающиеся с нетерминала

S и дающие терминальные

цепочки, в которых на последнем шаге не применяется

ε-правило. В искомое

множество нужно включить префиксы этих терминальных цепочек длиной 2

символа, а если они короче, то включить их целиком.

Любой вывод имеет единственное начало:

S AB. Любое продолжение даст

результат вида S AB

Aw, где w ∈V

— некоторая терминальная цепочка.

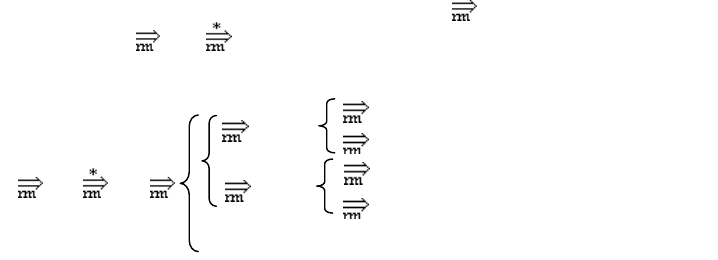
Далее возможны следующие продолжения:

Таким образом, функция

EFF

(S)={сb, сa}, тогда как функция

FIRST

(S)={ε, a, b, c, ab, ac, ba, ca, cb}.

Теорема 3.1. Чтобы контекстно-свободная грамматика G=(V

, V

, P, S)

была LR

(k)-грамматикой, необходимо и достаточно, чтобы выполнялось сле-

дующее условие: если

[A →β., u] — LR(k)-ситуация, допустимая для активного

префикса αβ правосентенциальной формы αβw пополненной грамматики G

’

где u=

FIRST

(w), то не существует никакой другой LR(k)-ситуации

→β

.β

, v], которая отличается от данной и допустима для активного

префикса αβ при условии, что u ∈

EFF

(β

v) (в частности, и при β

= ε).

Доказательство.

Необходимость. Предположим, что G — LR(k)-грамматика. Докажем, что

тогда условие выполняется.

S AB Aw

w — недопустимо (ε-правило).

Cbaw

Caw

caw,

aw — недопустимо (ε-правило);

cbaw,

baw — недопустимо (ε-правило);

204

По определению [

A →β., u] — LR(k)-ситуация, допустимая для активного

префикса

αβ правосентенциальной формы αβw пополненной грамматики G

’

если существует правосторонний вывод вида

’

αAw

αβw и u =

FIRST

(w).

Рассуждая от противного, предположим, что [

→β

.β

, v] — другая LR(k)-си-

туация, допустимая для активного префикса

αβ, причем u ∈

EFF

(β

v).

Согласно определению

LR(k)-ситуации, допустимой для активного префикса

αβ, существует вывод вида

’

y = αβy,

в котором применено правило

→β

и α

= αβ, β

x y, v =

FIRST

(x).

Кроме того, выполняется условие

u =

FIRST

(w) ∈

EFF

(β

v).

Условие 3)

u ∈

EFF

(β

v) означает согласно определению

EFF

, что суще-

ствует вывод вида

uz, в котором |u| = k и z ∈V

или |u| < k и z = ε, причем

если предпоследняя сентенциальная форма в этом выводе начинается с нетер-

минала, то он заменяется непустой терминальной цепочкой.

Рассмотрим

три возможных варианта состава цепочки β

: 1)β

= ε; 2)β

∈V

;

содержит нетерминалы.

Вариант 1

: β

= ε. В этом случае из условия 3) следует, что u ∈

EFF

(v) и,

следовательно,

u = v. Соответственно вывод 2) фактически имеет вид

’) S’ α

x α

x = αβy.

Отсюда

= αβ и x = y; соответственно

FIRST

(y) =

FIRST

(x)=v = u.

Так как

FIRST

(w)=u, то имеем два правосторонних вывода: 1) и 2’), в ко-

торых

FIRST

(w)=

FIRST

(y).

По предположению [

A →β., u] ≠ [A

→β

.β

, v], причем u = v. Следователь-

но, либо

A ≠ A

, либо β≠β

(ведь β

= ε). Но так как G — LR(k)-грамматика, то

должно выполняться равенство

x = αAy, (3.4)

в котором

x = y. При A ≠ A

это невозможно. Если же A = A

, то имеем α

≠α,

поскольку в этом случае

β≠β

при том, что α

= αβ. Итак, условие (3.4) не со-

блюдается, и

G — не LR(k)-грамматика вопреки первоначальному предположе-

нию. Полученное противоречие доказывает необходимость сформулированного

в теореме условия в данном частном случае.

Вариант 2

: β

= z, z ∈V

(

— непустая терминальная цепочка). В этом слу-

чае вывод 2) имеет вид

205

”) S

’

x = α

zx = αβy, так что α

= αβ, y = zx и, кроме то-

го, предполагается, что

”) u ∈

EFF

(β

x)=

EFF

(zx)=

EFF

(y)=

FIRST

(y), т.е. u =

FIRST

(y).

Итак, в выводах 1) и 2)

FIRST

(w)=

FIRST

(y).

Чтобы грамматика

G была LR(k)-грамматикой, должно быть α

x = αAy

или, что то же самое,

x = αAzx, но это невозможно при z ≠ε. Получается,

что

G — не LR(k)-грамматика, а это противоречит исходному предположению.

Данное противоречие доказывает неправомерность предположения о

существовании двух разных

LR(k)-ситуаций, о которых шла речь.

Вариант 3

: цепочка β

не пуста и содержит, по крайней мере, один нетерми-

нал. Пусть

B — самый левый из них, т.е. β

= u

Bδ, где u

∈V

, B∈V

δ∈(V

∪V

)

. Имеем:

’

αAw

αβw и

FIRST

(w) = u.

’

x = αββ

x, где α

= αβ,

FIRST

(x) = v.

u ∈

EFF

(β

v).

В этом варианте из условия 3) следует, что существует правосторонний вы-

вод

v = u

Bδv u

v u

v, u =

FIRST

v).

Здесь на последнем шаге используется правило

→ u

, где u

∈V

с гарантией,

что

≠ε. Действительно, если u

= ε, то в соответствии с определением

EFF

должно быть

≠ε.

Продолжим

вывод 2), учитывая, что β

= u

Bδ

’

) S

’

x = αβu

Bδx

αβu

x = αβy, где y = u

x, v =

FIRST

(x).

Вычислим

FIRST

(y ):

FIRST

(y )=

FIRST

x)=

FIRST

v)=u.

Итак,

FIRST

(w)=u,

FIRST

( y)=u, т.е.

FIRST

(w)=

FIRST

( y), и остает-

ся проверить, выполняется ли

LR(k)-условие αβu

x = αAu

x. Для

выполнения этого равенства необходимо, по крайней мере, чтобы

x = u

x, т.е. u

= ε, чего, как мы выяснили, нет (u

≠ε).

Таким образом,

LR(k)-условие нарушено, и G — не LR(k)-грамматика вопре-

ки исходному предположению.

Рассмотренные варианты состава цепочки

исчерпывающе доказывают не-

обходимость сформулированного условия.

Достаточность. Рассуждая от противного, предположим, что условие тео-

ремы выполнено, но

G — не LR(k)-грамматика. Согласно лемме 3.2 существуют

два вывода вида

206

’

αAw

αβw;

’

γBx

γδx = αβy, такие, что x, y, w ∈V

а)

FIRST

(w) =

FIRST

( y),

б)

γBx ≠αAy,

в)

|γδ|≥|αβ|.

Не ограничивая общности рассуждений, можно считать, что

αβ — одна из

самых коротких цепочек, удовлетворяющих описанным условиям.

Представим вывод 2) иначе, выделив в нем явно начальный участок, на ко-

тором получается

последняя цепочка, причем ее открытая часть не длиннее

|αβ| +1:

’

) S

’

αβy,

здесь

|α

|≤|αβ|+1 или, что то же самое, |α

|≤|αβ|≤|γδ|, A

→β

∈P.

Цепочка

— основа сентенциальной формы α

, причем β

— ее пре-

фикс такой длины, что выполняется равенство

|α

| = |αβ|.

Отметим, что активный префикс длиной

|αβ|, для которого допустима хотя

бы какая-нибудь

LR(k)-ситуация, не может получиться из сентенциальной фор-

мы, открытая часть которой длиннее

|αβ|+1. Действительно, если, например,

|α

| > |αβ|+1, т.е. |α

| > |αβ|, то крайний левый символ основы β

находил-

ся бы в позиции,

по меньшей мере, |αβ|+2, и эта основа не имела бы никакого

касательства к префиксу длиной |αβ|. Очевидно, что в выводе 2

’

) β

y и

= αβ.Таким образом, вывод 2

’

) можно переписать в следующем виде:

”

) S

’

= αββ

αβy.

Из факта

существования вывода 1) следует, что LR(k)-ситуация [A →β., u],

где u =

FIRST

(w), допустима для активного префикса αβ правосентенциальной

формы

αβw.

Аналогично из факта существования вывода

”

) следует, что LR(k)-ситуа-ция

[

→β

.β

, v], где v =

FIRST

), допустима для активного префикса αβ право-

сентенциальной формы

αββ

Учитывая условие a), вывод

y и равенство v =

FIRST

), заключа-

ем,

что

u =

FIRST

(w)=

FIRST

(y)∈

FIRST

(β

FIRST

(β

)⊕

FIRST

(β

) ⊕

{v}=

FIRST

(β

) ⊕

FIRST

(v)=

FIRST

(β

v).

Остается

показать, что u∈

EFF

(β

v). Действительно, если бы

u ∉

EFF

(β

v), то только потому, что цепочка β

начилась бы с нетерминала,

который на последнем шаге вывода

y замещался бы ε-цепочкой. Сопос-

тавим

исходное представление вывода 2) с его же представлением в виде 2

”

207

’

γBx

γδx = αβy

”

) S

’

= αββ

αβy.

Последним замещаемым нетерминалом в этом выводе является

B, причем эта-то

последняя замена и дает цепочку

αβy. На завершающем участке этого вывода

используется

y, так что, если β

= A

и последнее используемое правило

есть

B→ ε, то вывод 2

”

) можно переписать следующим образом:

’

= α

m–1

… y

m–1

… y

= α

m–1

… y

m–1

… y

= αβy,

где

= αβ, A

= B, y

m–1

… y

= y.

Отметим, что

|α

B| = |αβ|+1, но это противоречит предположению, что

— последняя цепочка в этом выводе, открытая часть которой имеет дли-

ну, не превосходящую величину

|αβ| +1. Следовательно, u ∈

EFF

(β

v).

Мы нашли две

LR(k)-ситуации, допустимые для одного и того же активного

префикса

αβ: [A →β., u] и [A

→β

.β

, v] при том, что u ∈

EFF

(β

v). Поскольку

с самого начала предполагалось, что не существует двух таких

разных LR(k)-

ситуаций, то должно быть [

A →β., u]=[A

→β

.β

, v]. Из этого равенства следу-

ет:

A = A

, β = β

, β

= ε.

Кроме того, поскольку α

= αβ, а β

= β, то α

= α. С

учетом этого вывод 2

”

) можем переписать так:

”

) S

’

αAy

αβy

= αβy, откуда заключаем, что y

= y.

Не забывая, что это другой вид того же самого вывода 2), заменим цепочку

на

A, и получим цепочку αβy, которая совпадает с предыдущей сентенциальной

формой в этом выводе. Это означает нарушение условия б)

γBx ≠αAy. Данное

противоречие — следствие неправомерного допущения, что

G — не LR(k)-

грамматика. Следовательно,

G — LR(k)-грамматика. Достаточность доказана.

Теорема также доказана.

Определение 3.8. Пусть G =(V

, V

, P, S) — контекстно-свободная грамма-

тика и

γ∈(V

∪V

)

— некоторый ее активный префикс. Определим множество

(γ) как множество всех LR(k)-ситуаций, допустимых для γ:

(γ)={[A →β

.β

, u]|∃A →β

∈P; ∃

’

αAw

αβ

w, γ = αβ

u =

FIRST

(w)}.

Множество

S = {A | A =

(γ), где γ — активный префикс G } назовем сис-

темой множеств LR(k)-ситуаций для грамматики G.

Алгоритм 3.2: вычисление множества

(γ).

Вход: G =(V

, V

, P, S) — контекстно-свободная грамматика, γ = X

...X

∈V

∪V

, i =1, 2,…, m; m ≥ 0.

208

Выход: множество

(γ).

Метод.

Будем строить последовательность множеств

(ε),

),...,

...X

)

1. Строится множество

(ε).

а) Инициализация:

(ε) = {[S→.α, ε] | ∃ S → α∈P }.

б)

Замыкание

(ε): если [A → .Bα, u] ∈

(ε), где B ∈V

, и существует

B →β∈P, то [B → .β, v], где v ∈

FIRST

(αu), тоже включается в множество

(ε).

в) Шаг б) повторяется до тех пор, пока во множестве

(ε) не будут про-

смотрены все имеющиеся в нем

LR(k)-ситуации. Замыкание завершается за ко-

нечное число шагов, так как множества

P и V

конечны.

2. Строится следующий элемент последовательности. Пусть множества

...X

), где 0 ≤ i < m, уже построены. Покажем, как построить следующее

множество

...X

i +1

а)

Инициализация: если [A →β

i +1

, u] ∈

...X

), то LR(k)-ситуация

[

A →β

i +1

.β

, u] включается в множество

...X

i +1

б)

Замыкание

...X

i +1

): если {[A →β

.Bβ

, u]∈

...X

i +1

), где

B ∈V

, и существует B →β∈P, то [B → .β, v], где v ∈

FIRST

(β

u), тоже вклю-

чается в множество

...X

i +1

в) Шаг б) повторяется до тех пор, пока во множестве

...X

i +1

) не бу-

дут просмотрены все имеющиеся в нем

LR(k)-ситуации. Замыкание завершается

за конечное число шагов, так как множества

P и V

конечны.

3. Шаг 2 повторять до тех пор, пока i < m.

4. Процесс завершается при i = m;

(γ)=

...X

Замечание 3.2. Алгоритм 3.2 не требует использования пополненной грамматики.

Определение 3.9. Пусть G =(V

, V

, P, S) — контекстно-свободная грамма-

тика. На множестве

LR(k)-ситуаций в этой грамматике определим функцию:

GOTO(

A, X )=A’, где A =

(γ) — некоторое множество LR(k)-ситуаций,

допустимых для активного префикса

γ∈(V

∪V

)

; X ∈V

∪V

; A’=

(γX).

Очевидно, что эта функция строится попутно с построением множеств

(γ)

на шаге 2 алгоритма 3.2: если множество

...X

) уже построено, то

...X

i +1

) = GOTO(

...X

), X

i +1

209

Остается ввести лишь обозначения:

γ = X

...X

, X = X

i +1

, A =

...X

A’=

...X

i +1

), чтобы увидеть, как это делается.

Замечание 3.3. Важно отметить, что результат функции GOTO(A, X )=A’, где A =

...X

), зависит не от X

...X

, а от

...X

Пример 3.9. Рассмотрим пополненную грамматику примера 3.1, содержа-

щую правила: 0)

’

→ S, 1) S → SaSb, 2) S →ε. Построим множества

(ε),

(S),

(Sa).

1: построение множества

(ε).

а)

(ε) = {[S

’

→ .S, ε]}.

б) Множество

(ε) пополняется ситуациями [S → .SaSb, ε], [S → ., ε];

множество

(ε) пополняется ситуациями [S → .SaSb, a], [S → ., a].

Другие шаги алгоритма 3.2 никаких других элементов в множество

(ε) не

добавляют. Окончательно получаем

(ε) = {[S

’

→ .S, ε], [S → .SaSb, ε], [S → ., ε], [S → .SaSb, a], [S → ., a]}.

сокращенных обозначениях то же самое принято записывать следующим

образом:

(ε) = {[S

’

→ .S, ε], [S → .SaSb, ε | a], [S → ., ε | a]}.

2: построение множества

(S ).

а)

(S) = {[S

’

→ S., ε], [S → S.aSb, ε | a]}.

Так

как точка ни в одной из этих ситуаций не стоит перед нетерминалом, то

шаг б) не выполняется ни разу. Попутно мы вычислили GOTO(

(ε), S)=

(S).

3: построение множества

(Sa).

а)

(Sa) = {[S → Sa.Sb, ε | a]}.

б) Множество

(Sa) пополняется ситуациями [S → .SaSb, b] и [S → ., b];

множество

(Sa) пополняется ситуациями [S → .SaSb, a] и [S → ., a].

Здесь шаг б) замыкания выполнялся дважды.

Итак,

(Sa)={[S → Sa.Sb, ε | a], [S → .SaSb, a | b], [S → ., a | b]} и

GOTO(

(S), a)=

(Sa).

Теорема 3.2. Алгоритм 3.2 правильно вычисляет

(γ), где γ∈(V

∪V

)

—

активный префикс правосентенциальной формы в грамматике G.

Доказательство. Фактически требуется доказать, что

LR(k)-ситуация

[

A →β

.β

, u] ∈

(γ) тогда и только тогда, когда существует правосторонний