Martin P.M. Handbook of Deposition Technologies for Films and Coatings, Third Edition: Science, Applications and Technology

Подождите немного. Документ загружается.

Evaporation 151

4.4 Theory and Mechanisms

4.4.1 Vacuum Evaporation

Reference to the various steps in the formation of a deposit enumerated in the previous section

shows that the theory of vacuum evaporation involves thermodynamic considerations, i.e.

phase transitions from which the equilibrium vapor phase pressure of materials can be derived,

as well as the kinetic aspects of nucleation and growth. Both of these are of obvious

importance in the evolution of the microstructure of the deposit.

The transition of solids or liquids into the gaseous state can be considered to be a macroscopic

or an atomistic phenomenon. The former is based on thermodynamics and results in an

understanding of evaporation rates, source-container reactions and the accompanying effect of

impurity introduction into the vapor state, changes in composition during alloy evaporation,

and stability of compounds. An excellent detailed treatment of the thermodynamic and kinetic

bases of evaporation processes is given by Glang [6]. He points out that the application of

kinetic gas theory to interpret evaporation phenomena resulted in a specialized evaporation

theory. Such well-known scientists as Hertz, Knudsen, and Langnuir were the early workers in

evaporation theory. They observed deviations from ideal behavior which led to reﬁnements in

the theory to include concepts of reaction kinetics, thermodynamics, and solid state theory.

From the kinetic theory of gases, the relationship between the impingement rate of gas

molecules and their partial pressure, p,isgivenby

= (2 πmkT )

−

p (4.2)

where N

is the number of molecules striking a unit area of surface, and A

is the area of the

surface.

Hertz [77], in 1882, ﬁrst measured the evaporation rate of mercury in high vacuum and found

that the evaporation rate was proportional to the difference between the equilibrium vapor

pressure of mercury, p*, at the evaporant surface and the hydrostatic pressure, p, acting on the

surface, resulting from the evaporant atoms or molecules in the gas phase. Thus, the

evaporation rate based on the concept of the equilibrium vapor pressure (i.e. the number of

atoms leaving the evaporant surface is equal to the number returning to the surface) is given by:

(2πmkT )

−

(p* − p)cm

−1

(4.3)

such that dN

, the number of molecules evaporating from a surface area A

in time dt, is equal

to the impingement rate of gas molecules based on the kinetic theory of gases with the value of

p* inserted therein, minus the return ﬂux corresponding to the hydrostatic pressure p of the

evaporant in the gas phase. In the above equations, m is the molecular weight, k is

152 Chapter 4

Boltzmann’s constant, and T is the temperature in K. The maximum possible evaporation rate

corresponds to the condition p = 0. Hertz measured evaporation rates only about one-tenth as

high as the theoretical maximum rates. The latter were subsequently measured by Knudsen

[78] in 1915. Knudsen postulated that some of the molecules impinging on the surface were

reﬂecting back into the gas phase rather than becoming incorporated into the liquid. As a

result, there is a certain fraction (1 − α

) of vapor molecules which contribute to the evaporant

pressure but not to the net molecular ﬂux from the condensed phase into the vapor phase. To

this end, he postulated the evaporation coefﬁcient, α

, which is deﬁned as the ratio of the real

evaporation rate in vacuum to the theoretically possible value deﬁned by Eq. (4.3). This then

results in the well-known Hertz–Knudsen equation:

= α

(2πmkT )

−

(p* − p) (4.4)

The value of α

is very dependent on the cleanliness of the evaporant surface and can range

from very low values for dirty surfaces to unity for clean surfaces. In very high-rate evaporation

with a clean evaporant surface, it has been found that the maximum evaporation given by Eq.

(4.4) has been exceeded by a factor of 2–3 for the evaporation of a light metal such as

beryllium [21] using e-beam heating. The reason for this is that the high power input results in

considerable agitation of the liquid evaporant pool resulting in a real surface area much larger

than the apparent surface area. The directionality of evaporating molecules from an

evaporation source is given by the well-known cosine law. Figure 4.11 shows a small surface

Figure 4.11: Surface element dA

receiving deposit from a small area source dA

. (From

McGraw-Hill Book Company.)

Evaporation 153

element dA

receiving deposit from a small area source dA

. The mass deposited per unit area

(σ, θ )

πr

cosϕ cosθ (4.5)

where M

is total mass evaporated.

For a point source, Eq. (4.5) reduces to:

πr

cosϕ (4.6)

For a uniform deposit thickness, the point source must be located at the center of the spherical

receiving surface such that r is a constant and cosθ =1.

In high-rate evaporation conditions, e.g. using a high-power e-beam-heated source, the

thickness distribution is steeper than with a point or small area source discussed above. This

has been attributed by some authors [33, 34, 79] to the existence of a virtual source of vapor

located above the molten pool. On the other hand, at high power, the e-beam impact area on

the surface of the molten pool is not ﬂat but pushed down into an approximate concave

spherical segment which, as Riley shows [80], can equally well account for the steeper

thickness distribution.

The above discussion points out one of the problems with evaporation technology, i.e. the

variation in thickness of the deposit on a ﬂat substrate. Numerous solutions are possible which

involve either moving the substrate in a manner so as to randomly sample the vapor ﬂux, the

use of multiple sources, or sources of special shapes. These have been discussed in some detail

by Holland [8] as well as by Bunshah and Juntz [81].

Models have also been presented for calculating the deposit temperature [82] and thickness

distribution [83] during high-rate evaporation and veriﬁed against experimental data. In a more

recent paper, Szekely and Poveromo [84] have given a more general formulation describing

the net rate of vapor deposition from a molten source onto an initial cold surface, making

allowance for both molecular transport and diffusion effects.

With PVD metal can be also be evaporated, vaporized, and then condensed in the form of

nanoparticles. Okuyama et al. reported production of ultraﬁne metal oxide aerosol particles by

thermal decomposition of metal alkoxide vapors [85]. A comprehensive study on the growth

dynamics of the particles is presented by Flagan et al. [86]. The temperature required for

vaporization can be achieved by Joule heating, although thermal plasmas [87], laser ablation

[88], and spark ablation sources [89] operate in the same manner. In these processes vapors

migrate from the hot source into a cooler gas by a combination of convective ﬂows and

diffusion. Although dilution resulting from the latter transport mechanism decreases the partial

154 Chapter 4

pressure of the vapor from the saturation condition at the source, the decreasing temperature

leads to a far more rapid decrease in the equilibrium vapor pressure and correspondingly high

supersaturation. Nanostructured materials can be synthesized by condensation from the vapor

phase in the presence of inert carrier gas, most often in a buoyant plume above a hot vapor

source. Particle growth in these condensation processes can be classiﬁed into three stages as

nucleation, coalescent coagulation, and agglomerate growth. The growth characteristics are

determined by both the probability for interparticle collisions due to Brownian motion and the

velocity of interparticle coalescence. Furthermore, agglomeration is characterized by the

equality of the characteristic collision and coalescence times, denoted by τ

col

and τ

coa

respectively. The coalescence time is mainly determined by the diffusivity and, thus, depends

strongly not only on the temperature, but also on the activation energy and the diffusion

constant. If we consider surface diffusion the predominant sintering mechanism, the following

equations for the coalescence and collision times can be obtained [86, 90, 92]:

coa

∝ d · T exp





col

∝ d

−

(4.7)

where d, T, E

, and k

denote the particle diameter, the temperature, the activation energy for

diffusion, and the Boltzman constant, respectively.

The metal atoms effused from the source will rapidly lose their energy by collision with carrier

gas atoms. The nucleation process is performed homogeneously in the vapor phase and the

collision mean free path is very short, i.e. in the order of 100 nm. If one further assumes a

steady-state cluster formation and distribution is considered, the nucleation rate depends on

the supersaturation of metal vapor in the gas phase, S [86]:

J ∝ exp



−σ



(4.8)

where σ is the surface tension. The free energy barrier against nucleation is also a function of

σ and S as follows [92, 93]:

G =

(ρRT lnS)

(4.9)

where ρ is the particle density, R is the gas constant, and T is temperature. Since the

supersaturation of metal vapor is caused by the collision of the metal atoms with the gas

atoms, the amount of undercooling determines the supersaturation and thus the nucleation

process. It is known that the value of vapor phase undercooling depends on the evaporation

temperature. This model has been applied on Ag nanoparticles prepared by IGC [92, 93].

Evaporation 155

4.5 Evaporation Process and Apparatus

4.5.1 The System

A schematic of the evaporation apparatus has been illustrated in Figure 4.1. It consists of the

following: chamber, vacuum pumps, vacuum gauges, including total and partial pressure

gauges on sophisticated systems, evaporation sources, substrate holders, rate monitors, process

controller, etc.

4.5.1.1 Vacuum Chamber

This ranges from a simple bell jar or rectangular box for experimental or batch type production

to more complex gear for production applications. The latter may consist of a deposition

chamber with loading and unloading chambers attached to the deposition chambers by

manifolds with isolation high-vacuum valves. These are called fast cycle coaters. Alternate

approaches are semi-continuous in-line systems where a strip substrate stored in the vacuum

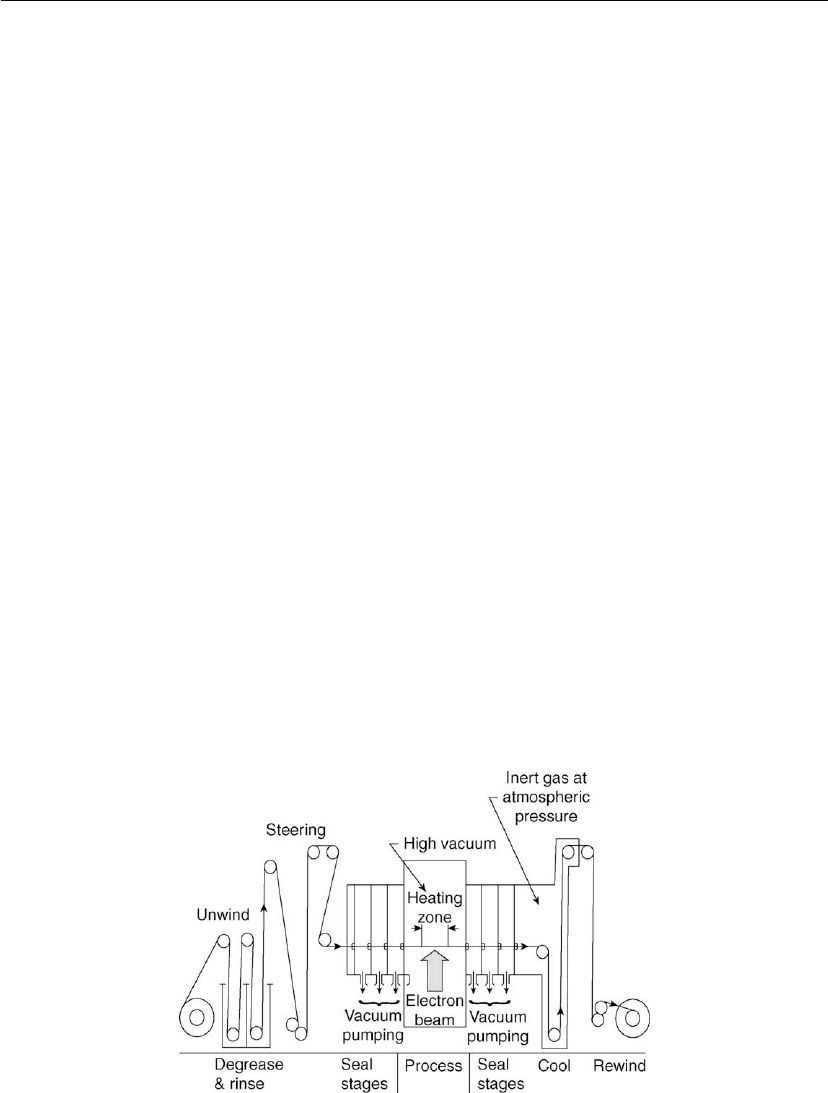
chamber can be fed continuously over the source (Figure 4.12) or a continuous system where

the strip or sheet substrate is inserted and removed from the deposition chamber through

air-to-air seals [4, 94] (Figures 4.13 and 4.14).

4.5.1.2 Vacuum Pumping System

The gas loads in evaporation processes are fairly high owing to outgassing from chamber walls

promoted by the heat load from the evaporation source and substrate heaters, particularly for

high deposition rate conditions. Therefore the pumping system is usually based on a diffusion

pump with a liquid nitrogen cooled anticreep type bafﬂe backed with a mechanical pump or a

Roots blower/mechanical pump combination for large systems. For very high-purity,

Figure 4.12: Schematic representation of a 24 inch continuous high vacuum strip processing line.

156 Chapter 4

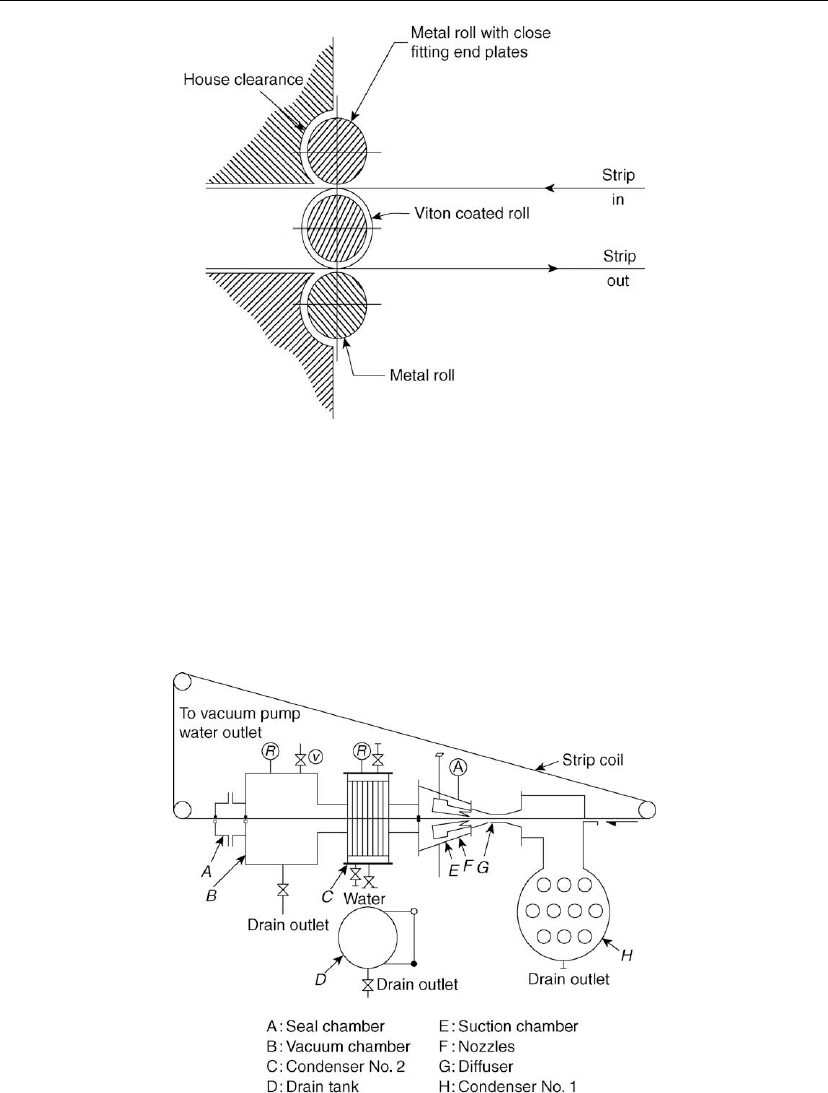
Figure 4.13: Three-high roll seal arrangement for stripline.

low-deposition rate, low-heat ﬂux conditions, ion pumped systems backed with cryosorption

rough pumping are used, since a base pressure of 10

−9

–10

−10

torr is needed. More recently,

turbomolecular and cryogenic pumps have been used instead of diffusion pumps where desired

(e.g. oil-free systems). This is particularly true for molecular beam epitaxy where extreme

Figure 4.14: Vacuum seal using steam jet or curtain.

Evaporation 157

control over composition and layer thickness is essential and deposition rates can be quite low.

In such cases, the chamber and pumps are to be baked as with any other ultrahigh vacuum

operation.

4.5.1.3 Pressure Measurement

The vacuum gauges used depend again on speciﬁc applications, such as a combination of

high-pressure gauges (such as the Pirani or Thermocouple Gauge) for monitoring the roughing

of the system and high-vacuum gauges (such as the hot cathode ionization gauge and/or

capacitance manometer). A partial pressure gauge is highly desirable, particularly for

ultraclean applications, as well as for leak hunting.

4.5.1.4 Evaporation Sources

These are discussed separately in Section 4.6.

4.5.1.5 Substrate Holders and Heaters

Substrate holders may be very simple for stationary ﬂat substrates or can incorporate quite

complex motions as illustrated by planetary or rotating devices. The reason for this is to ensure

deposition thickness uniformity and control over a large number of small parts such as lenses

or silicon wafers. Substrate heating can be accomplished by radiant heaters with refractory

wires or quartz lamps acting as the heat source. Occasionally, substrates are directly heated by

a scanning or diffuse e-beam.

4.5.1.6 Deposition Rate Monitors

These are discussed in Section 4.7.

4.6 Evaporation Sources

4.6.1 General Considerations

Evaporation sources are classiﬁed by the mode of heating used to convert the solid or liquid

evaporant to the vapor phase. Thus one talks of resistance, arc, induction, electron beam, arc

imaging, lasers, and exploding wire types of sources. It is very important to note that we

cannot evaporate every material from any of the types of sources listed above, for the

following reasons:



chemical interaction between the source material and the evaporant would lead to

impurities in the deposit. For example, evaporation of titanium from a MgO source

would cause oxygen and magnesium contamination of the deposit; the titanium would

reduce the MgO. Therefore, for the evaporation of reactive metals such as titanium or

zirconium, water-cooled copper crucibles are used

158 Chapter 4

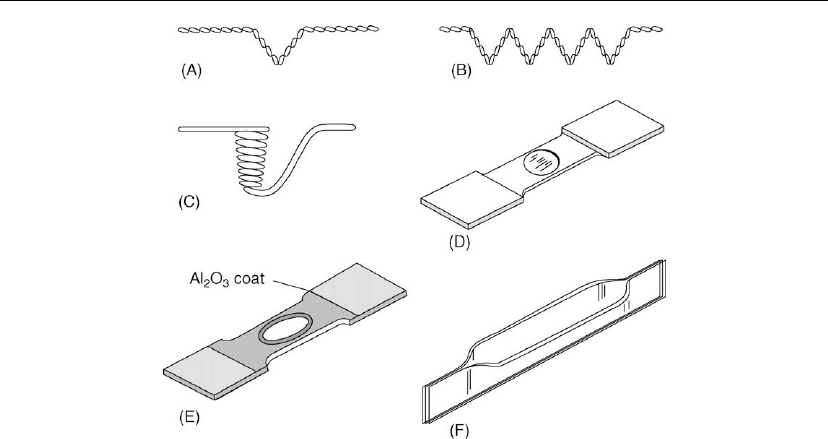
Figure 4.15: Wire and metal-foil sources: (A) hairpin source; (B) wire helix; (C) wire basket; (D)

dimpled foil; (E) dimpled f oil with alumina coating; (F) canoe type. (From Handbook of Thin Film



reaction between metallic source (such asaWorTaboat) and evaporant (Ti) could

occur. In many cases at high temperatures two metals can mutually dissolve in each

other, leading to destruction of the source



the power density (i.e. W/cm

) varies greatly between the various heat sources.

Table 4.2, from the article by Glang [6], lists the temperature and support materials to be used

in the evaporation of elements. Similar tables are found in the literature of many of the

manufacturers.

Evaporation of alloys and compounds poses additional problems, and they are considered in

Section 4.9.

4.6.2 Resistance-Heated Sources

The simplest vapor sources are resistance-heated wires and metal oils of various types shown

in Figure 4.15.

They are available in a variety of sizes and shapes and at sufﬁciently low prices so that they

can be discarded after one experiment if necessary. They are usually made from the refractory

metals, tungsten, molybdenum, and tantalum, which have high melting points and low vapor

pressure so as not to contaminate the deposit. Their properties are given in Table 4.3.

Evaporation 159

Table 4.2: Temperatures and support materials used in the evaporation of the elements

Element and

predominant

vapor species

Temp. (

◦

C) Suppor t materials Remarks

mp p*=10

−1

torr Wire, foil Crucible

Aluminum (Al) 650 1220 W C, BN, TiB

-BN Wets all materials readily and tends to

creep out of containers. Alloys with W

and reacts with carbon. Nitride crucibles

preferred

Antimony (Sb

)

630 530 Mo, Ta, Ni Oxides, BN,

metals, C

Polyatomic vapor, ˛

= 0.2. Requires

temperatures above mp. Toxic

Arcenic (As

)

820 ∼ 300 – Oxides, C Polyatomic vapor, ˛

=5.10

−6

–5.10

−2

Sublimates but requires temperatures

above 300

◦

C. Toxic

Barium (Ba) 710 610 W, Mo, Ta, Ni,

Metals Wets refractory metals without alloying.

Reacts with most oxides at elevated

temperatures

Beryllium (Be) 1283 1230 W, Mo, Ta C, refractory

oxides

Wets refractory metals. Toxic,

particularly BeO dust

Bismuth (Bi, Bis) 271 870 W, Mo, Ta, Ni Oxides, C,

metals

Vapors are toxic

Boron (B) 2100 ± 100 2000 – C Deposits from carbon supports are

probably not pure boron

Cadmium (Cd) 321 265 W, Mo, Ta, Fe,

Oxides metals Film condensation requires high

supersaturation. Sublimates, Wall

deposits of Cd spoil vacuum system

Calcium (Ca) 850 800 W Al

Carbon (C

,C,

)

∼ 3700 ∼ 2600 – – Carbon-arc or electron-bombardment

evaporation. ˛

(Continued)

160 Chapter 4

Table 4.2: (Continued)

Element and

predominant

vapor species

Temp. (

◦

C) Suppor t materials Remarks

mp p*=10

−1

Torr Wire, foil Crucible

Chromium (Cr) ∼ 1900 1400 W, Ta – High evaporation rates without melting.

Sublimation from radiation-heated Cr

rods preferred. Cr electrodeposits are

likely to release hydrogen

Cobalt (Co) 1495 1520 W Al

, BeO Alloys with W, charge should not weigh

more than 30% of ﬁlament to limit

destruction. Small sublimation rates

possible

Copper (Cu) 1084 1260 W, Mo, Ta Mo, C, Al

Practically no interaction with refractory

materials. Mo preferred for crucibles

because it can be machined and

conducts heat well

Gallium (Ga) 30 1130 – Beo, Al

Alloys with refractory metals. The oxides

are attacked above 1000

◦

Germanium

(Ge)

940 1400 W, Mo, Ta W, C, Al

Wets refractory metals but low solubility

in W. Purest ﬁlms by electron-gun

evaporation

Gold (Au) 1063 1400 W, Mo Mo, C Reacts with Ta, wets W and Mo. Mo

crucibles last for several evaporations

Indium (In) 156 950 W, Mo Mo, C Mo boats preferred

Iron (Fe) 1538 1480 W Beo, Al

ZrO

Alloys with all refractory metals. Charge

should not weigh more than 30% of W

ﬁlament to limit destruction. Small

sublimation rates possible

Lead (Pb) 328 715 W, Mo, Ni, Fe Metals Does not wet refractory metals. Toxic

Magnesium

(Mg)

650 440 W, Mo, Ta, Ni Fe, C Sublimates