Marcus P. Corrosion mechanisms in theory and practice

Подождите немного. Документ загружается.

a predictable change in crack propagation rate of about a factor of 4. It follows,

therefore, that the practical use of such a prediction methodology for life predic-

tion, codification, etc. hinges on an adequate definition of the actual system via the

use of system monitors for corrosion potential, solution conductivity, etc. [2].

Integration of the crack propagation rate algorithms leads to an appropriate

crack depth—time (a – t) relationship, which, for a uniform tensile stress situation,

is of the form

624 Ford and Andresen

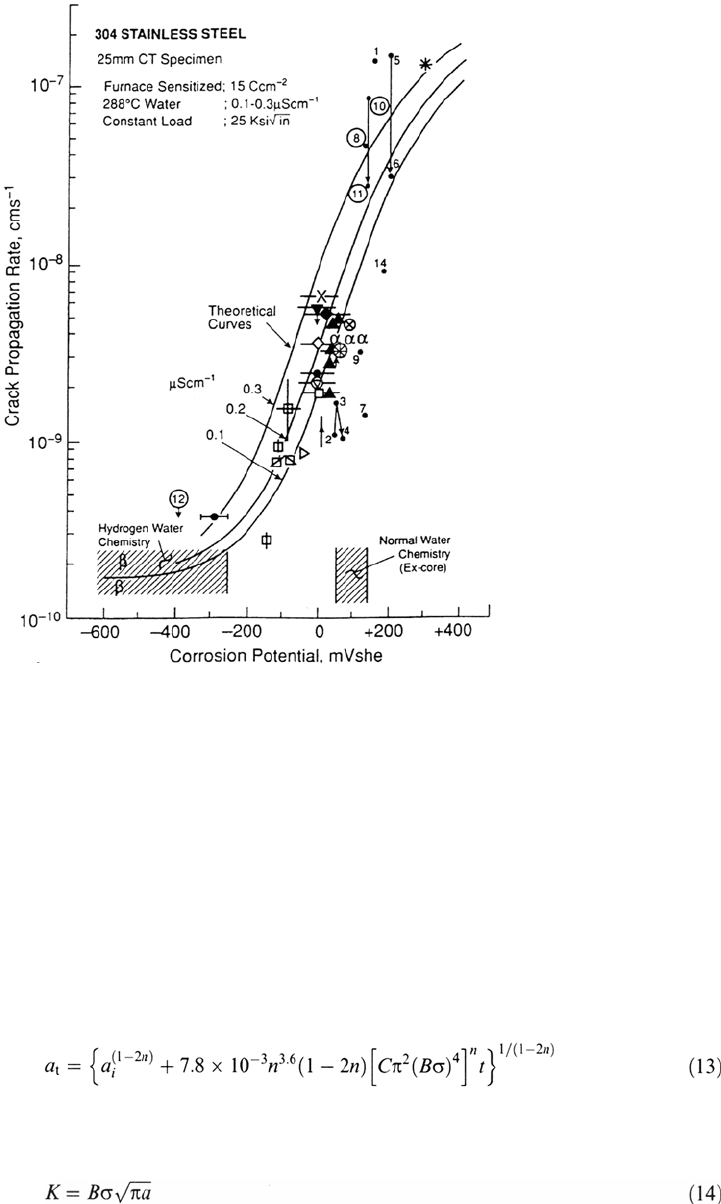
Figure 14 Observed and predicted relationships between the crack propagation rate and

corrosion potential for sensitized type 304 stainless steel in water under constant load. Water

conductivity in range 0.1 to 0.3 μS/cm. (From Ref. 1).

This particular form applies in the simple case in which the stress intensity can

be defined by

These formulations can become more complicated, e.g., for complex stress

fields adjacent to welds. Examination of Eq. (13) indicates that, at time zero, there

is an assumed intrinsic initiating defect, a

; in the following analyses for “smooth”

stainless steel components, a value of 50 μm has been used [2,10].

Equation (13), in conjunction with the variation in stress intensity as a crack

grows through a residual stress field adjacent to a weld, provides a prediction of the

effects of, e.g., (a) water purity on the crack depth–operating time for stainless steel

piping and (b) a range in residual stress on the predicted range of crack depths in a

piping system (Fig. 18). A range in actual system conditions inherently leads to a

predicted range in cracking response, as illustrated in Figure 19 for the theoretical

relationships between the coolant purity and the operating time required for a crack

to penetrate 25% of the wall thickness in a welded type 304 stainless steel pipe. These

theoretical relationships are shown for typical ranges in carbon contents (i.e., EPR

values) and in residual stress profiles. Figure 19 shows that the observed data

lie within the theoretical bounds. Thus, with this proven prediction capability,

quantitative decisions can be made about the future behavior for proposed

modifications in environment, material, or stress (Fig. 20).

Similar predictions can be made for the effect of irradiation on the

intergranular cracking susceptibility of stainless steel components in the reactor

core [114]. The prediction methodology developed for unirradiated conditions was

modified to account for the effect of fast neutron and gamma irradiation on (a)

Corrosion in Nuclear Systems 625

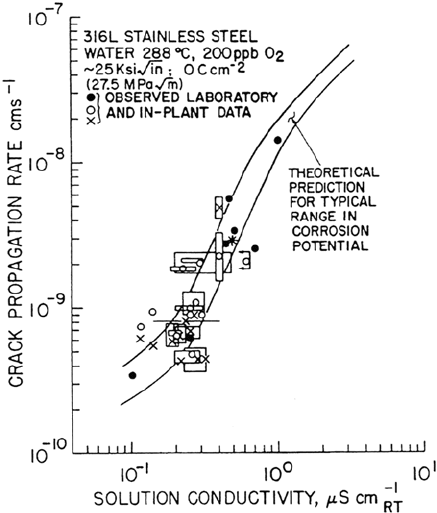
Figure 15 Observed and predicted relationships between the crack propagation rate and

solution conductivity for type 316L stainless steel under constant load (25 ksi √

—

in) in water

containing 200 ppm oxygen. (From Ref. 1).

irradiation hardening and its effect on crack tip strain rates, (b) irradiation-induced

relaxation of residual stresses, (c) irradiation-induced depletion or enrichment of

compositional elements species at the grain boundary, and (d) the corrosion

potential via the radiolysis of water.

Once these individual effects have been qualified and verified, it is

relatively easy to extend the existing prediction methodology for IGSCC of

unirradiated stainless steels to cover the effects of fast neutron fluence on the

time to failure of stainless steels in oxygenated water (Fig. 21). Figure 22

shows the predicted variation of a “threshold” fluence (below which cracking is

not observed in, e.g., 10 operating years) for different combinations of stress and

626 Ford and Andresen

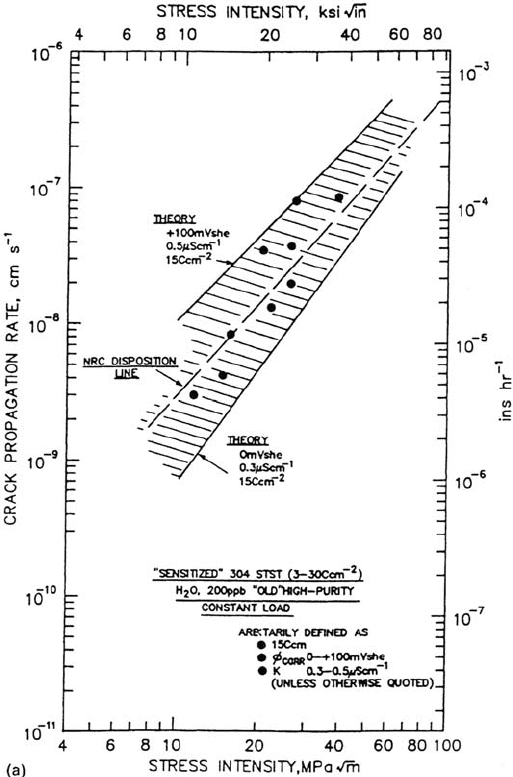
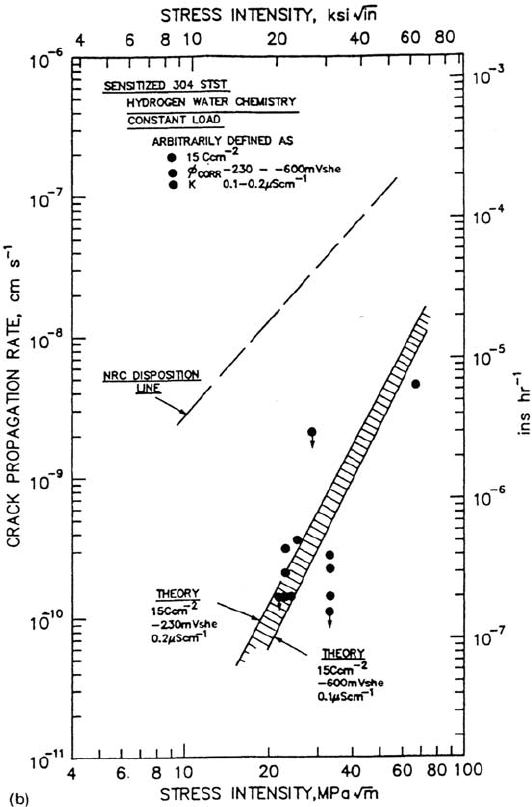
Figure 16 Comparison between observed and theoretical crack propagation rate–stress

intensity relationships for sensitized type 304 stainless steel in water at 288°C; 200 ppb

; 0.2 to 0.5 μS/cm.

solution purity. Moreover, specific remedial actions can be defined to arrest

cracking which is detected in a reactor component. For example, Figure 23

shows the changes in corrosion potential necessary to arrest a crack in a BWR

core shroud.

Low-Alloy Steel/ BWR System

It is assumed that the slip dissolution model is applicable to transgranular

environmentally assisted cracking in the A533B/A508 low-alloy steel–water system at

288°C [1]. It is recognized that this assumption may introduce a systematic error due

Corrosion in Nuclear Systems 627

Figure 16 (Continued)

to undefined components of crack advance associated with film-induced cleavage or

hydrogen embrittlement, but this is regarded as a small error at this stage of the life

prediction methodology development [1,113]. Thus, Eq. (5) is retained as the primary

basis for prediction, and its quantification has been accomplished [1,79,113] in a

similar manner to that described for stainless steel. A primary difference, however,

has been the unique role played by the dissolution of MnS inclusions and the

associated definition of the crack tip environment [1,79,80]. This is addressed in

detail elsewhere [1,79,80,115–119], and it should merely be recognized that MnS

inclusions do dissolve in high-temperature water. The dissolution rate is sufficiently

rapid to increase the concentration of dissolved sulfur species in the crack and,

thereby, to increase the crack growth rate significantly. Other influential factors,

such as anion enhancement in the crack due to a gradient in potential down the

crack and anion deletion due to flushing of the crack at high bulk solution flow

rates, are also important, as in stainless steel.

The agreement between theory and observation of cracking under laboratory

conditions is encouraging [1,79], as in the agreement between the observed and

theoretical crack depth–operating time relationships for cracks in the limited number

of incidences of cracking in A508 feedwater nozzles of BWR reactors (Fig. 24). In

this latter case, cracks were observed to initiate on the surface due to thermal fatigue

628 Ford and Andresen

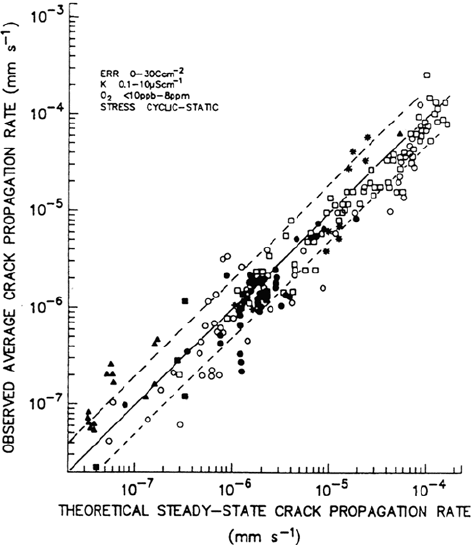
Figure 17 Relationship between the observed and theoretical steady-state propagation

rates for stainless steel in water at 288°C for a wide combination of material, stress, and

environment conditions. (From Ref. 1.)

Corrosion in Nuclear Systems 629

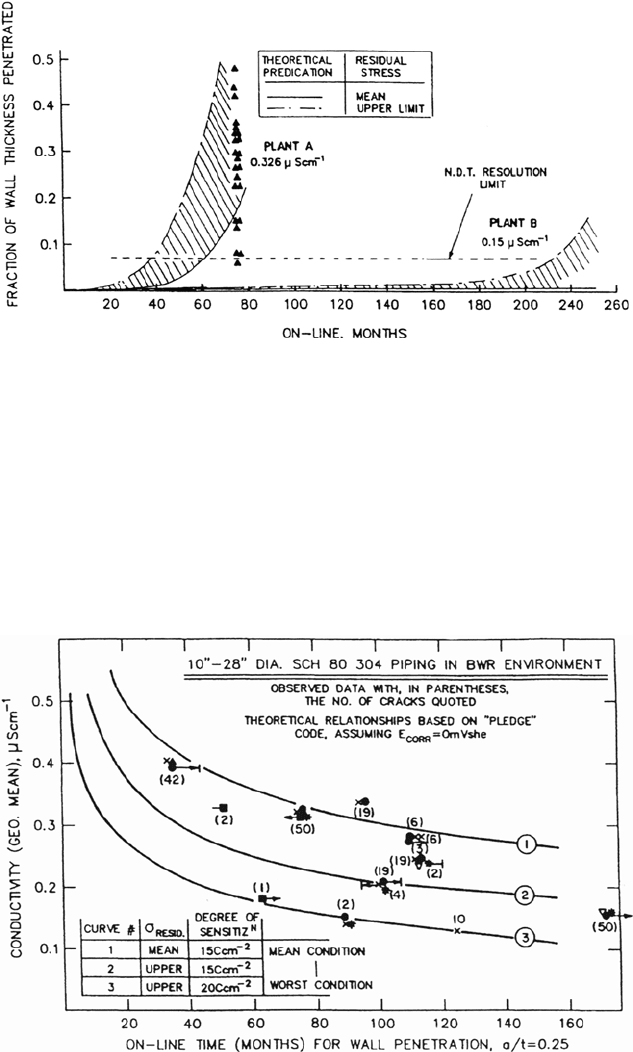
Figure 18 Theoretical and observed crack depth vs. operational time relationships for

28-inch-diameter schedule 80 type 304 stainless steel piping for two BWRs operating

at different mean coolant conductivities. Note the bracketing of the maximum crack depth

in the lower-purity plant by the predicted curve that is based on the maximum residual stress

profile and the predicted absence of observable cracking in the higher-purity plant (in 240

operating months).

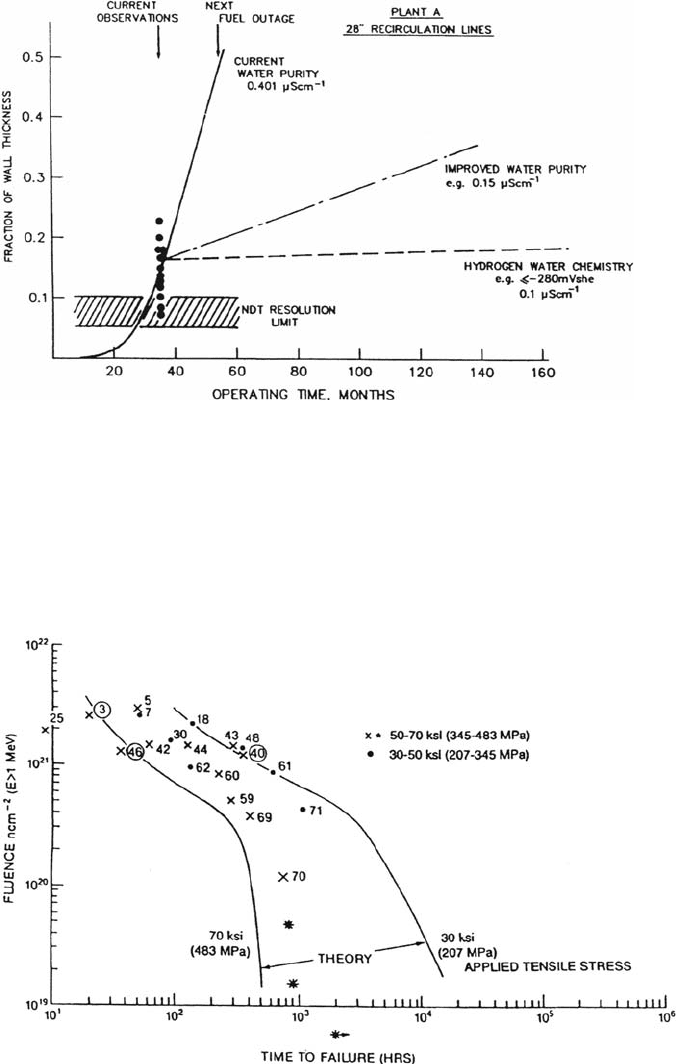
Figure 19 Observed and theoretical relationships between average BWR coolant

conductivity and the operational time to achieve quarter wall penetration. Observed data

from various operational BWRs are shown with the number of cracks detected shown in

parentheses beside each data point. Theoretical curves are for the quoted combinations of

stress and degree of sensitization at the HAZ.

630 Ford and Andresen

Figure 20 Predicted response of defected piping for defined changes in water chemistry

in BWR plant.

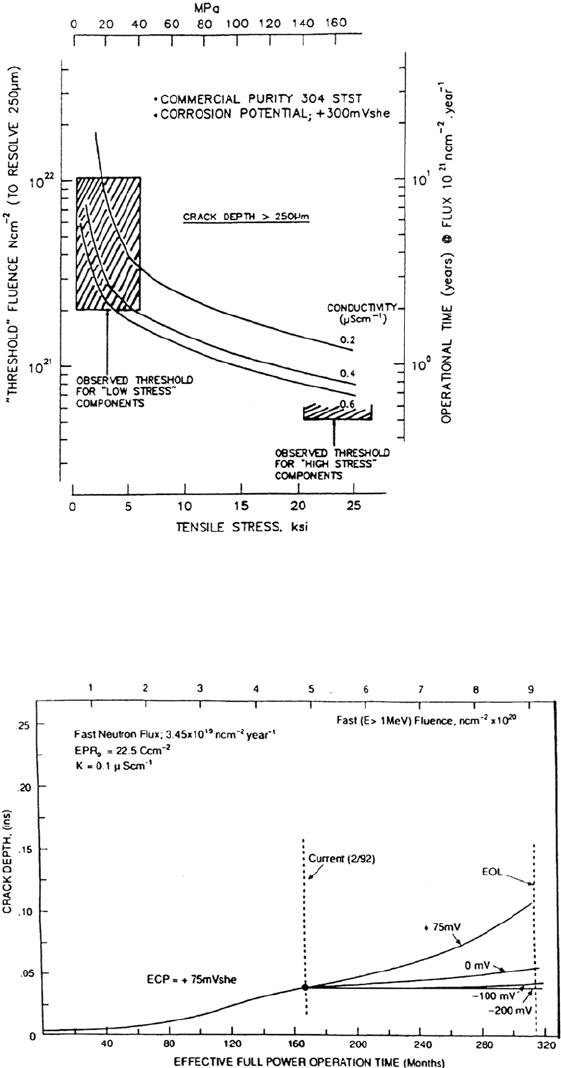
Figure 21 Comparison between observed and theoretical relationships for the effect of

fast neutron fluence on the time to failure of irradiated type 304 stainless steel under constant

load in 32 ppm oxygenated water at 288°C.

Corrosion in Nuclear Systems 631

Figure 22 Predicted and observed variations between threshold fluence for observation

of cracks in irradiated BWR components and the tensile stress and solution conductivity.

Figure 23 Predicted crack depth–time relationship for cracking in a hypothetical BWR

core shroud and the defined changes in corrosion potential required to slow down and

arrest the crack propagtion.

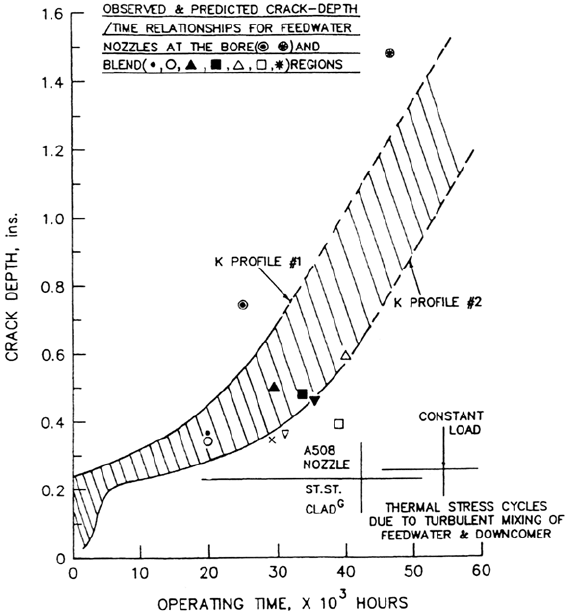
caused by mixing of hot water coolant and the cooler feedwater, and the theoretical

analysis [79] addressed the subsequent propagation of these cracks due to stress

corrosion from pressurization stresses alone.

As with stainless steels, the stress corrosion predictions can be logically

expanded to cover corrosion fatigue. Corrosion fatigue of low-alloy steels in LWR

environments and the impact on ASME XI life evaluation analyses have been

exhaustively reported [115–117]. In summary, the current ASME XI code for

corrosion fatigue crack propagation of low-alloy steels can be overly conservative

under certain operating conditions; however, under specific conditions of low

cyclic frequencies, high oxygen content environments, and high-sulfur steels, it is

predicted and observed that (da/dN)

ΔK

values greater than the ASME XI code

curve are possible [118].

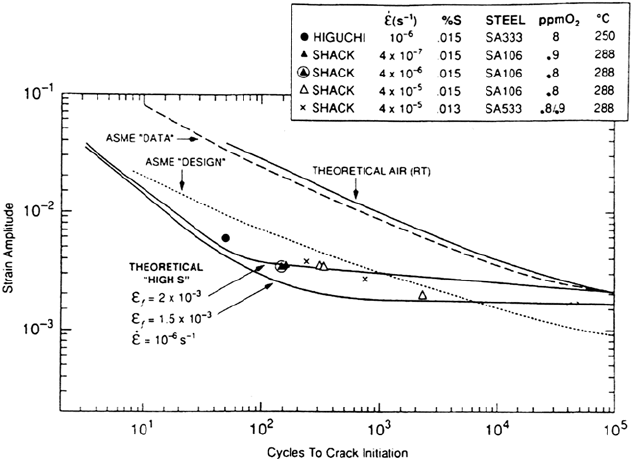
The validity of the current ASME III code for corrosion fatigue crack initiation

in low-alloy and carbon steels in LWR environments is under current review [119].

Although the model development actions are still in a preliminary stage, it is

apparent that the cycles to crack initiation (N

) are predictable and that the conditions

under which the ASME III design curve is nonconservative can be defined (Fig. 25).

632 Ford and Andresen

Figure 24 Predicted and observed crack depth–operating time relationships in BWR

feedwater nozzles. (From Ref. 79.)

The laboratory and field experiences base for environmentally assisted

cracking low-alloy steel is far smaller than for sensitized stainless steel, and more

development and validation work is required before the prediction methodology

can responsibly be reduced to practice.

Nickel-Base Alloys/BWR System

The development of prediction models for environmentally assisted cracking of

nickel-base alloys in BWR systems is made difficult by the fact that the data base

against which the prediction models can be validated exhibits extreme scatter

(Fig. 26) and/or was obtained under conditions which are not directly applicable to

BWR operation (e.g., high conductivity). Establishing a link between crack growth

rates in stainless steels and ductile nickel-base alloys helps to resolve this problem,

since it permits the much broader base of data and modeling for stainless steels to

provide guidance on the expected response of nickel-base alloys in BWR systems

[70,120]. This mechanistic link is reasonable for the following reasons:

• Intergranular cracking is the dominant failure mode and is associated with

chromium depletion at the grain boundary in both types of alloys. For

stainless steels, EPR is used to quantify sensitization, as described above.

However, the EPR technique cannot be used without significant modification

Corrosion in Nuclear Systems 633

Figure 25 Predicted [119] and observed [121–123] strain amplitude vs. cycles to intiation

relationships for (unnotched) carbon and low-alloy steels in high-temperature water, under

the worst combination of material and environmental conditions. Note that carbon and

low-alloy steels behave very similarly, with a N

/Δ∈

response in high oxygen 250/288°C

water which is dictated by the high sulfur content of the steel.