Marcus P. Corrosion mechanisms in theory and practice

Подождите немного. Документ загружается.

In a similar way, for the reaction

4 Landolt

the Nernst equation reads

At 25°C this becomes

In this equation E

Zn (OH)

/Zn

= –0.439 is the standard potential for the formation of

a hydrated zinc oxide [2].

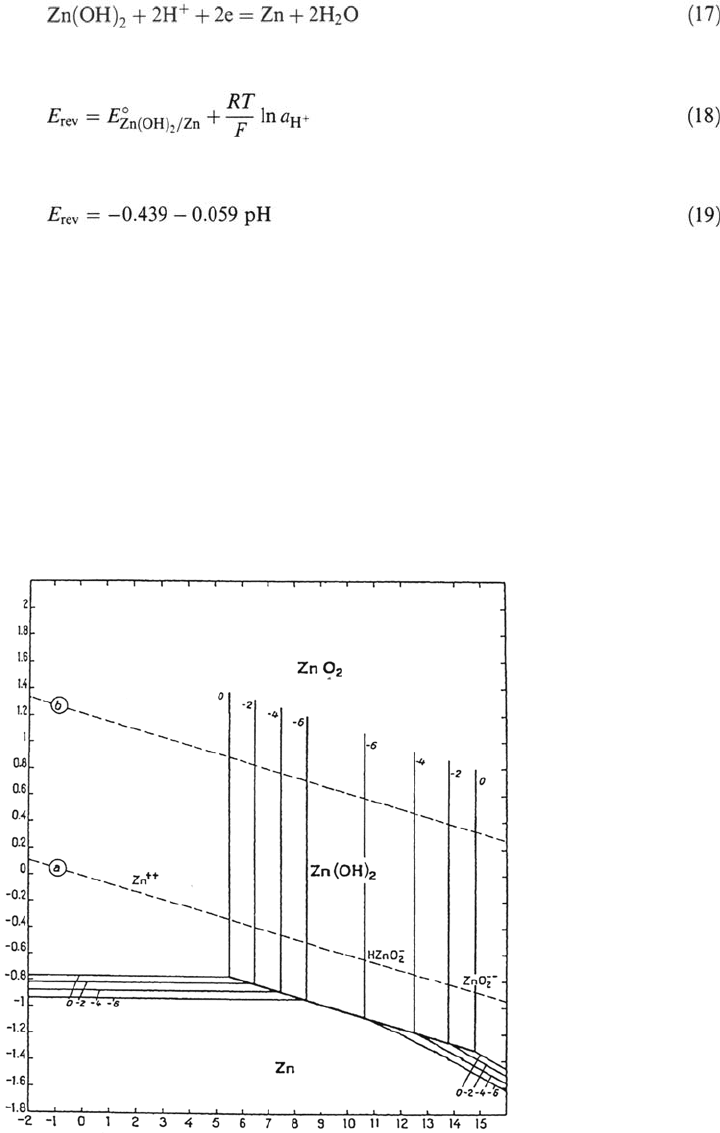
Pourbaix Diagrams

The graphical representation of the reversible potential as a function of pH is called

the potential-pH diagram or Pourbaix diagram. In order to trace such diagrams one

must fix the concentration of the dissolved species. Figure 1 shows a simplified

Pourbaix diagram for zinc [2]. The numbers indicate different concentrations of

Figure 1 Potential-pH diagram of Zu (From Ref. 2).

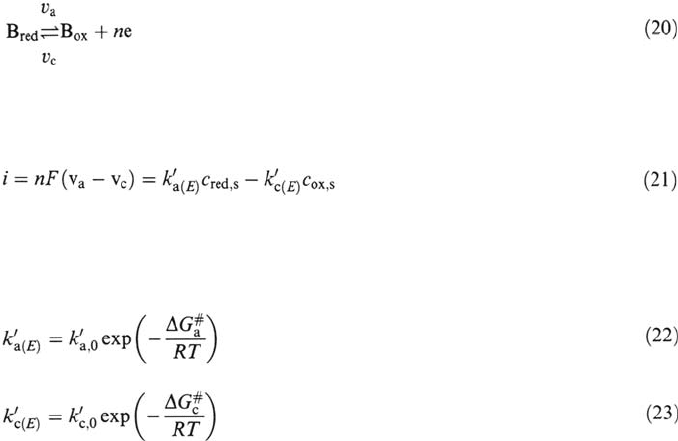
dissolved species, for example, 10

–2

, 10

–4

mol/L. The diagram shown takes into

account the formation of zinc hydroxide, of Zn

and of the zincate ions HZnO

–

and ZnO

2–

. At high potentials ZnO

may possibly be formed, but because the

corresponding thermodynamic data are uncertain they are not presented in the

diagram. The broken lines indicate the domain of thermodynamic stability of

water. Pourbaix diagrams are widely used in corrosion because they easily permit

one to identify the predominant species at equilibrium for a given potential

and pH. On the other hand, being based on thermodynamic data, they give no

information on the rate of possible corrosion reactions.

KINETICS OF CHARGE TRANSFER REACTIONS

At the electrode-electrolyte interface, a charge separation between the metal surface

and the electrolyte occurs. The spatial region corresponding to the charge separation

is called the electrical double layer. It is usually separated into two parts, the

Helmholtz layer or compact double layer and Gouy-Chapman layer or diffuse

double layer. The relative importance of the diffuse double layer increases with

decreasing concentration. In very dilute solutions it may extend over a distance of

several nanometers, whereas the compact layer never exceeds two to three tenths

of a nanometer. The charges at the interface establish an electric field. Within the

compact double layer the electric field reaches values of the order of 10

to 10

V/m. Charge transfer reactions occur across the compact double layer and the

influence of the diffuse double layer is usually neglected.

Let us consider the transfer of n electrons between two species, B

and B

red

Electrochemical Basis of Corrosion 5

According to Faraday’s law, the current density across the interface corresponding

to this reaction is equal to the difference of the anodic rate v

and the cathodic rate

multiplied by nF.

Here k′

a(E)

and k′

c(E)

are potential-dependent rate constants and c

red,s

and c

ox,s

rep-

resent the surface concentrations of B

red

and B

ox,

respectively. The rate constants

k′

and k′

obey the Arrhenius equation.

Here ΔG

and ΔG

represent the activation energies for the anodic and cathodic

partial reactions, respectively, and k′

a,0

and k′

c,0

are preexponential factors. The

presence of an electric field at the electrode-electrolyte interface modifies the

activation energy of the partial oxidation and reduction reactions as shown

schematically in Figure 2. The electric field in this case diminishes the activation

energy of the anodic partial reaction and increases that of the cathodic partial

reaction.

6 Landolt

Figure 2 Free energy as a function of the reaction coordinate showing the influence of

the electrical potential on the activation energy of a charge transfer process.

Here ΔG

a,ch

and ΔG

c,ch

represent the potential-independent parts of the activation

energies and ΔΦ represents the potential difference across the interface. The pro-

portionality factor α is called the charge transfer coefficient. Its value is usually

close to 0.5 [3]. The absolute value of ΔΦ is not measurable. It differs from the

electrode potential E measured with respect to the standard hydrogen reference

electrode by a constant.

Combining all potential-independent terms in the rate constants k

and k

one gets

With Eqs. (21) and (27) one obtains Eq. (28).

The current i corresponds to the sum of the partial anodic and cathodic current

densities:

The anodic and cathodic partial current densities, i

and i

, respectively, are

given by

Electrochemical Basis of Corrosion 7

At the reversible potential, E = E

rev

, the current density i is zero and the surface

concentration of the reacting species is equal to the bulk concentration: c

red,s

= c

red,b

and c

ox,s

= c

ox,b

. This allows one to define the exchange current density of a reaction

by the relation:

With (32) and (28) one gets

This expression shows that the value of the exchange current density depends on

the concentration of the participating species. Defining the overvoltage η =E – E

rev

Eqs. (33) and (28) yield (34).

If the rate of an electrode reaction is entirely controlled by charge transfer, the

concentrations of reactants and products at the electrode surface are equal to the

bulk concentrations. Equation (34) then reads

This is the usual form of the Butler-Volmer equation, which describes the relationship

between current density and potential for a simple electrode reaction controlled by

charge transfer.

Normally, multielectron transfer reactions proceed in subsequent one-electron

transfer reaction steps. For n > 1, Eq. (35), therefore, does not describe the physical

mechanism. Indeed, depending on which reaction step is rate limiting, the value

of the exponential terms may change. For example, the cathodic reduction of protons

corresponding to the overall reaction

proceeds in two steps. The Volmer-Heyrovsky mechanism applies to most metal

substrates:

On certain noble metals of the platinum group, however, the so-called Volmer-Tafel

mechanism applies:

In this case the second step is a chemical recombination reaction of adsorbed

hydrogen atoms produced in the first step, which according to the reaction

stoichiometry must proceed twice. The two mechanisms presented here and the

rate-determining steps can be distinguished by measuring Tafel slopes. For a more

detailed discussion of this point the reader may refer to the literature [3–6].

In corroding systems the detailed mechanisms of the partial electrode reactions

are frequently not known. Therefore, it has been found useful to introduce the

empirical Tafel coefficients β

and β

defined by

8 Landolt

Comparing these definitions with Eqs. (30) and (31), one finds β

= RT/αnF and

= RT/(1 – α)nF. Equation (35) thus becomes:

The Butler-Volmer equation written in the form (44) is frequently used in corrosion.

It describes the relationship between current density and potential of an electrode

reaction under charge transfer control in terms of three easily measurable

quantities: i

, β

, and β

. For large anodic overvoltages (η/β

>> 1) Eq. (44)

reduces to (45).

Taking the logarithm and defining a

= –2.303β

ln i

and b

= 2.303β

, this yields

the Tafel equation for an anodic reaction:

Analogously, for large cathodic overvoltages (η/β

<< –1):

Taking the logarithm and defining a

= –2.303β

ln i

and b

= 2.303β

yields the

Tafel equation for an cathodic reaction:

The Tafel equation applying to large overvoltages predicts a straight line for the

variation of the logarithm of current density with potential.

CHARGE TRANSFER REACTIONS AT MIXED ELECTRODES

If a metal is in contact with an electrolyte containing on oxidizing agent, two or more

electrode reactions can take place simultaneously. Such a system is called a mixed

electrode. Suppose a metal M dissolves while a species B

is reduced to B

red

Electrochemical Basis of Corrosion 9

The two partial reactions are

The total current density at the metal-solution interface is equal to the sum of the

anodic and cathodic partial current densities of the two electrode reactions.

The subscripts M and B designate the partial reactions and the subscripts a and c

stand for anodic and cathodic, respectively. Usually in a corroding system one can

neglect the cathodic partial current of the metal and the anodic partial current of

the oxidizing agent: i

c,M

≈ 0, i

a,B

≈ 0. Therefore (52) can be simplified:

At open circuit the mixed electrode is at its corrosion potential, E = E

cor,

and there

is no net current. Hence:

This allows one to define the corrosion current density i

cor

, which according to Eq.

(4) is proportional to the corrosion rate.

If charge transfer is rate limiting, the Butler-Volmer equation (35) described the

current-potential relationship of each partial reaction. With the overvoltage of the

metal dissolution reaction, η

= E – E

rev,M

, and for the reduction reaction, η

= E – E

rev,B

, one gets the following expression for the corrosion current density:

Equation (56) shows that the corrosion current density for a charge transfer–

controlled reaction is entirely determined by the kinetic parameters of the partial

electrode reactions involved.

By definition, the polarization ζ =E –E

cor

indicates the deviation of the

electrode potential from the corrosion potential. The polarization ζ is related to the

overvoltage of the partial electrode reactions by (57) and (58).

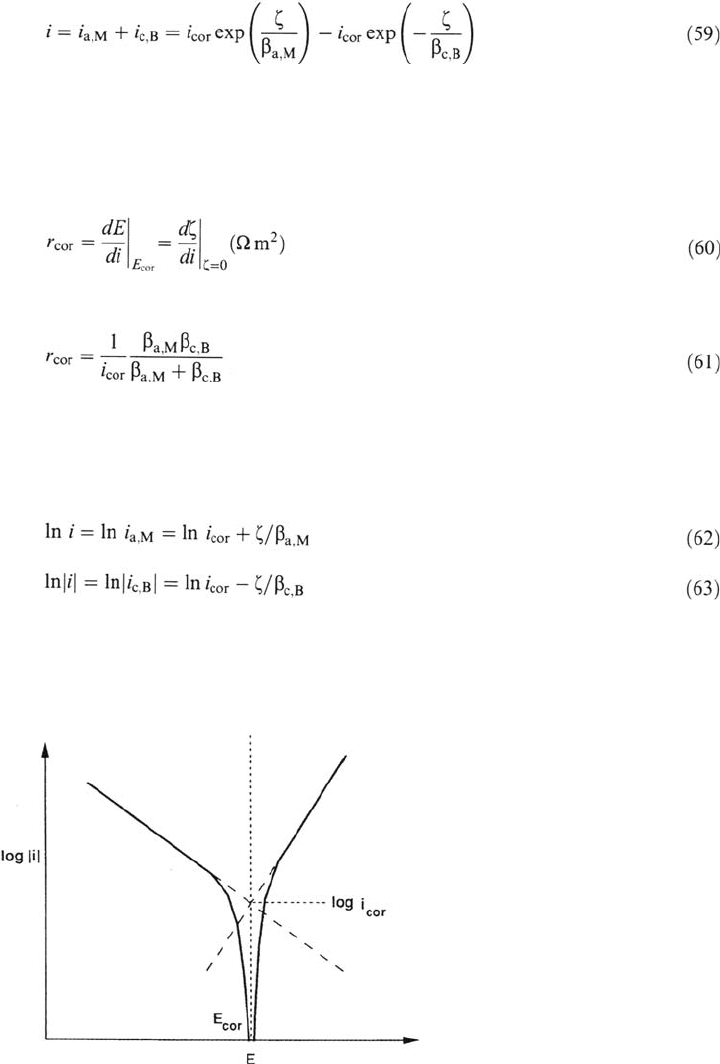
With these expressions one can easily derive the Butler-Volmer equation of a

mixed electrode corresponding to the corrosion reaction (49):

10 Landolt

At the corrosion potential the absolute values of the two partial current densities

are equal. The reciprocal of the slope of the curve i = f

(E)

is called polarization

resistance. A measurement of the polarization resistance at the corrosion potential,

cor

, allows one to determine the corrosion current density provided the anodic and

cathodic Tafel coefficients are known. By definition:

With Eq. (59) this yields

The value of the corrosion current density can also be obtained from a logarithmic

plot (Fig. 3) by extrapolating the anodic or the cathodic partial current density to

the corrosion potential. Indeed, for the anodic and cathodic Tafel regions,

respectively, Eq. (59) yields

Semilogarithmic plots of the partial anodic and cathodic current densities of mixed

electrodes as shown in Figure 3 are called Evans diagrams. The determination of the

Figure 3 Logarithmic presentation of current-potential curve of a mixed electrode

(Evans diagram) showing the corrosion potential E

cor

and the corrosion current density

cor

. The broken lines indicate the partial current densities.

corrosion rate from electrochemical polarization experiments was introduced by

Stern and Geary [7], but the development of the theory of mixed electrodes, due

to Wagner and Traud [8], dates much earlier.

MASS TRANSPORT-CONTROLLED ELECTRODE REACTIONS

For a corrosion reaction to take place, oxidizing agents must reach the electrode

surface. Similarly, reaction products must be eliminated from the electrode surface

by transport toward the bulk solution. If mass transport of reactants and products

is slow compared to charge transfer, their concentration at the electrode surface

differs from that in the bulk solution: the concentration of reactants diminishes,

that of products increases. Figure 4 shows the concentration profile of a reactant.

Three mechanisms contribute to mass transport: diffusion, convection, and migration.

For neutral species such as dissolved oxygen and for ionic species present in small

amounts in a supporting electrolyte, the contribution of migration is negligible.

Transport then occurs by diffusion and convection only. To describe transport

by diffusion and convection, one frequently uses the Nernst diffusion layer model,

which postulates that the electrolyte volume can be divided into two regions.

Near the electrode surface convection is negligible and transport occurs by

diffusion only. In the bulk electrolyte, on the other hand, the concentration is

uniform and no diffusion takes place. The thickness δ of the so-called

Nernstdiffusion layer is obtained by extrapolating the gradient at the surface (

= 0)

to the bulk concentrations (Fig. 4). Its value depends on convection conditions and

is typically of the order of a few micrometers [4].

Let us assume that the reaction rate for the reduction of an oxidant B

partly mass transfer controlled. If one neglects migration, the flux N

at the

electrode surface is given by Eq. (64).

Electrochemical Basis of Corrosion 11

Figure 4 Concentration of a reacting species as a function of distance from the electrode.

Integration over a constant diffusion layer thickness δ yields

12 Landolt

In these equations D

is the diffusion coefficient of B

and c

B,b

and c

B,s

indicate

the bulk and surface concentrations of B

, respectively. With Faraday’s law one

obtains for the cathodic partial current density:

This expression is valid at all potentials. If the potential becomes increasingly

cathodic the absolute value of the current density i

c,B

increases and, consequently,

b,s

decreases. Eventually, a condition is reached where c

B,s

becomes zero. This

situation corresponds to the maximum possible reaction rate, and the corresponding

current density is called the limiting current density i

Below the limiting current density, mass transport as well as charge transfer

determines the overall reaction rate. For η/β

c,B

<< – 1 the Butler-Volmer equation

(34) reduces to (68), where β

c,B

is the cathodic Tafel coefficient for the reaction of

species B.

Combining this expression with (66) and (67), one obtains (69) and (70).

If i

o,B

L,B

exp(–η/β

c,B

) <

l, Eq. (70) reduces to Eq. (47) describing a charge

transport–controlled cathodic reaction obeying Tafel kinetics. On the other hand,

if the absolute value of i

o,B

L,B

exp(–η/β

c,B

) is large compared with 1 Eq. (70)

becomes i

c,B

. At the limiting current density the reaction rate is entirely

controlled by the rate of mass transport and no longer depends on potential.

Figure 5 shows on a semilogarithmic plot a cathodic partial reaction

corresponding to Eq. (69). At low current densities the reaction follows Tafel

kinetics. As the current density increases, transport becomes more important and

eventually a limiting current plateau is reached. The figure also shows a charge

transfer–controlled anodic partial reaction. The corrosion potential is situated at

the intersection of the two curves, which is located on the limiting current

plateau of the cathodic partial reaction. The corrosion current density, therefore,

is equal to the limiting current density of the cathodic partial reaction. The rate of

corrosion in this case is mass transport controlled. Corrosion in neutral media in the

presence of dissolved oxygen frequently follows this mechanism.

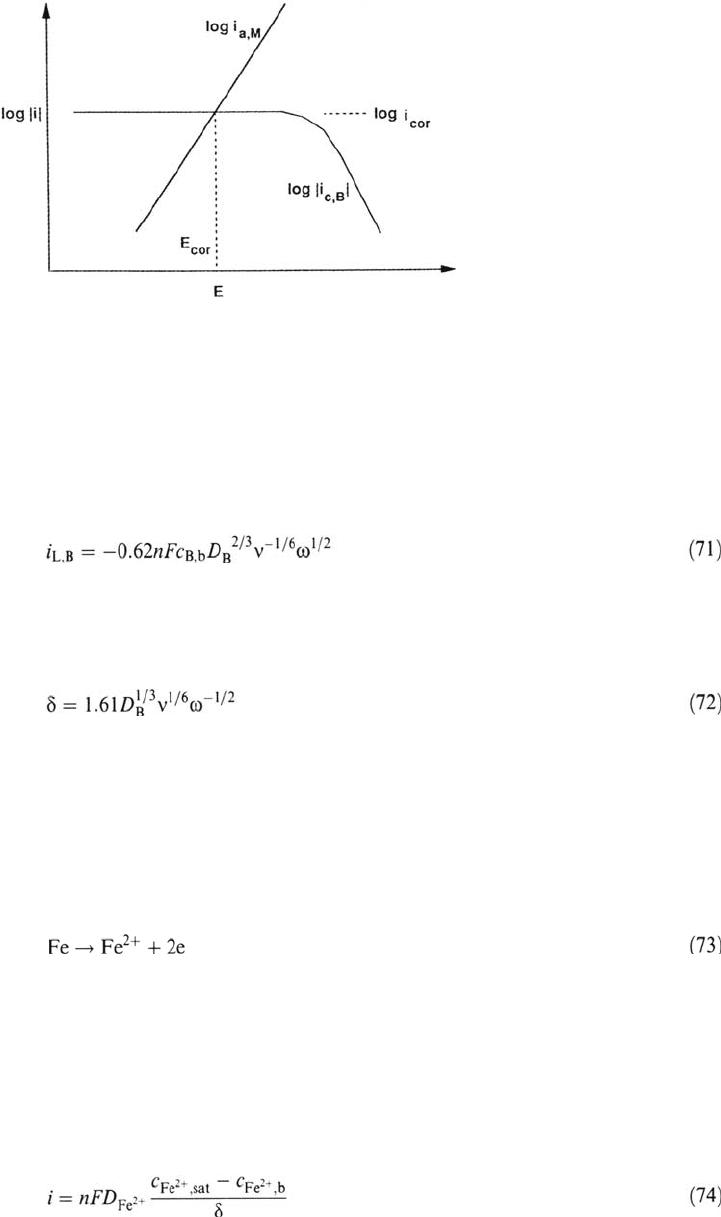
In the laboratory one frequently uses rotating-disk electrodes for the study of

mass transport effects. According to the Levich equation [9], the limiting current

density for a cathodic reaction at a rotating-disk electrode under laminar flow

conditions varies linearly with the square root of the rotation rate.

Electrochemical Basis of Corrosion 13

Figure 5 Evans diagram showing a cathodic partial reaction controlled by mass transport.

In this equation

represents the kinematic viscosity and ω the rotation rate in

rad/s. The other symbols have their usual meaning. Combining (71) with (67)

yields for the Nernst diffusion layer thickness:

According to (72), the value of δ depends on the diffusion coefficient of the reacting

species. This clearly shows that the Nernst diffusion layer is not a physical entity

but a theoretical concept permitting us to treat separately the contributions of

convection and diffusion to mass transport.

Under certain conditions the rate of transport of anodically formed dissolution

products may become rate limiting. For example, the dissolution of iron in

concentrated chloride media according to the reaction

leads to accumulation of ferrous ions in the diffusion layer. At sufficiently high

dissolution rates the concentration at the electrode surface reaches the saturation

concentration of ferrous chloride, causing the precipitation of a salt film on the

surface. This condition manifests itself by the appearance of a transport-controlled

current plateau on the current-potential curve. Neglecting migration, the limiting

dissolution current density is given by Eq. (74) where c

,sat

indicates the

saturation concentration of ferrous ions at the electrode surface.