Махкамов К.Х. Расчет износостойкости машин: учебное пособие
Подождите немного. Документ загружается.

51
()
(
)
() ()
−
+
−
−
=∆
3
1
2
2
2
2
3
1
1
1
2
1
3
2
1
3
2
2
1
3
2
1
3
2
ср
М
2
13
2
13
12/3
E
R
E
R
E
RP
W
ii
izi
µµ
µπτ
(2.64).
∆
=∆
t
z
m
W
i
i
i
2
И
(2.66),
(
)
2211
3
2
1
3
2
1ср
М
71,4 Γ+ΓΓ=∆
iizii
RRPRW
τ
(2.65).
Кинетическая энергия перемещений центров масс:
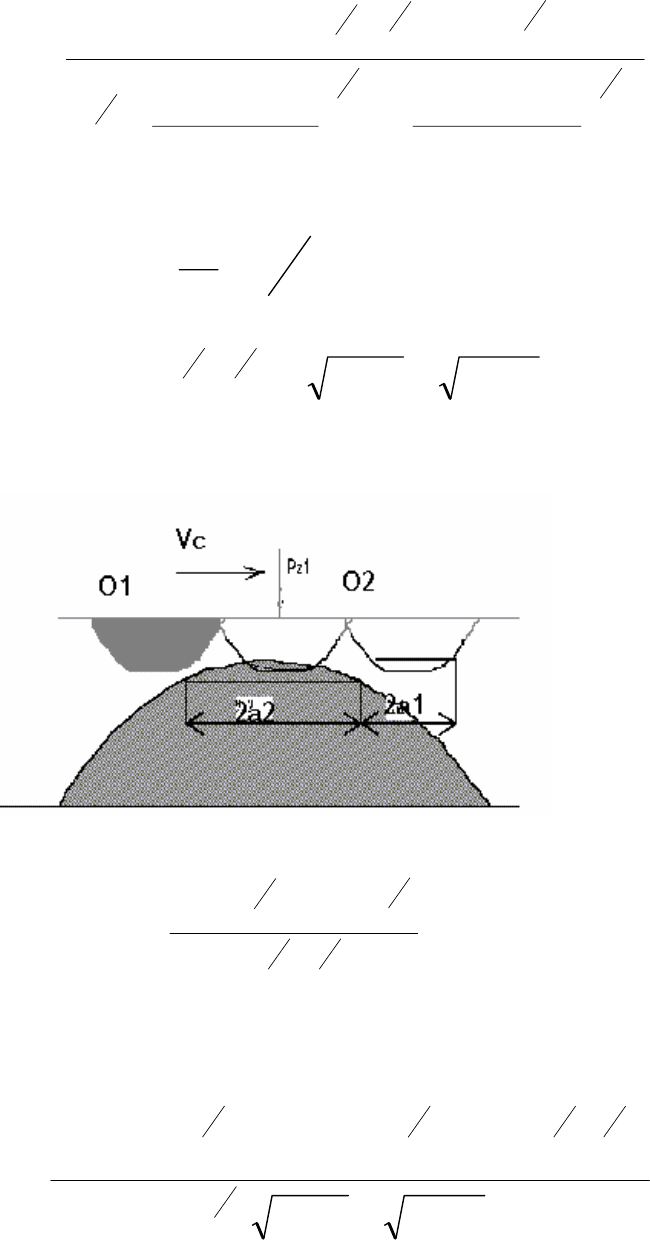
Рис 8. Схема взаимодействия сферических неровностей.
(
)
3
1
3
2
3
2
2
3
2
183,0
R
E
P
hz
zi
k
µ
−
==∆
(2.67).
Время
()
Vaat /
21
+=
;
ρ
сф
Vm
i
=
, (2.68)
()
2
3
22
3
11
3
5
1
3
2
1
3
2
3
4
1
22
3
8
11
и
1
69,093,31142,0
iii
ziizi
i
RRR
PRVP
W
Γ+Γ
Γ+Γ
=∆
ρ
(2.69)

52
()
2
3
22
3
11
3
5
2
3
2
2
3
2
3
4
2
22
3
8
22
и
2
69,093,31142,0
iii
ziizi
i
RRR
PRVP
W
Γ+Γ
Γ+Γ
=∆
ρ
(2.70)
По А.В.Чичинадзе [65]
11
22вз
1
1
1
C
CК
ϑ
ϑ
α
+
=−
, (2.71)
где 1 - α - количества тепла, идущее в тело 1; υ - температуропроводность; C -
удельная теплоёмкость.
Обозначим
11
22
С
С
ϑ
ϑ
ψ
=
, тогда:
2
1
2
2
1
2
вз
вз
К ;
1
1
1
a
a
S
S
К
==
+
=−
ψ
α
(2.72).
Тепловые потоки
()
ψ
α
3
2
2
3
2
2
3
2
1
3
2
1
3
2
1
3
2
1
1
1
ii
ii
i
RR
RJ
JJ
Γ+Γ
Γ
=−=
(2.76),
ψ
ψ
α
3
2
2
3
2
2
3
2
1
3
2
1
3
2
2
3
2
2
2
ii
ii
i
RR
RJ
JJ
Γ+Γ
Γ
==
(2.73),
где J - генерируемый тепловой поток при скольжении пятен контакта одной
фрикционной связи.
()
()()
ψ
τ
3
22
2
3
11
3
4
1
3
2
1
3
4
1
3
2
1
3
22
3
11ср
М
1
71,4
ii
ziiiii
i
RR
RRRRR
W
Γ+Γ
ΓΓΓ+Γ
=∆
; (2.74)
()
()()
ψ
ψτ
2
3
22
2
3
11
3
4
2
3
2
2
3
4
1
3
2
1
3
22
3
11ср
М
2
71,4
ii
ziiiii
i
RR
RRRRR
W
Γ+Γ
ΓΓΓ+Γ
=∆
; (2.75).
По Б.В.Протасову [46]
∑∑∑∑
====
∆+∆=
2211
11
2
11
1
m
i
n
j
ij
m
i
n
j
ij
DDЕ
(2.76),
53
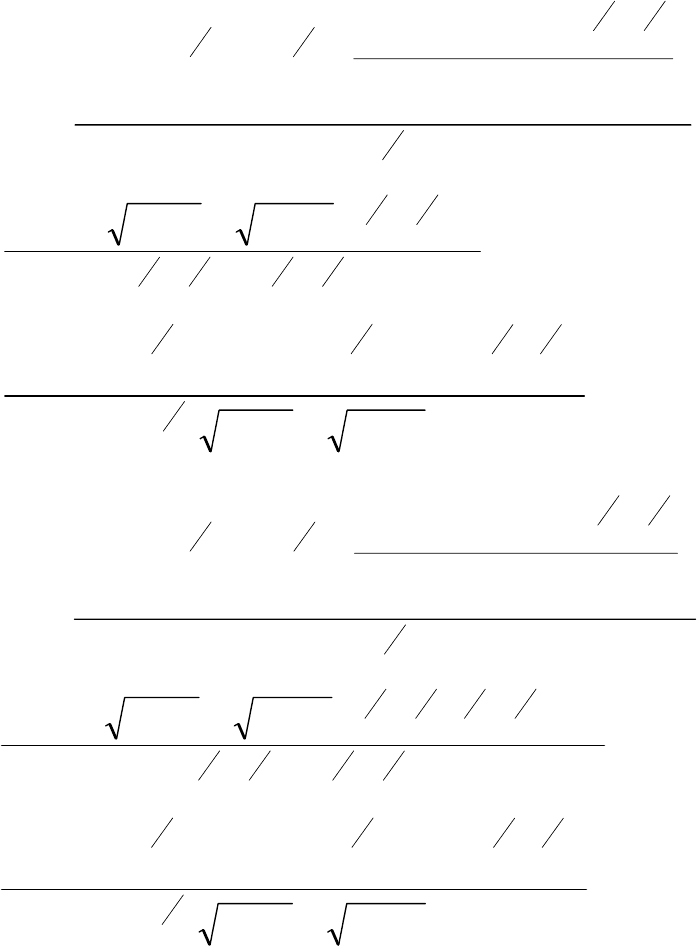
поскольку при взаимодействии Σ n = Σ n
1
= Σ n
2
∑∑∑
===
∆+∆=
т
о
m
i
ij
m
i
ij
DDЕ
11
2
1
1тр
21
, (2.77)
где ∆D
1ij
- энергия, рассеиваемая i-м элементом шероховатой поверхности тела 1 в
j-м взаимодействии; ∆D
2ij
- энергия, рассеиваемая i-м элементом шероховатой
поверхности тела 2 в j-м взаимодействии; n
1
, n
2
- число одновременно возникающих
фрикционных связей на всей площади контакта шероховатых поверхностей в j-м
взаимодействии за время t; m
1
, m
2
- число взаимодействий i-го элемента за время на
пути L.
Суммарная энергия диссипации в одном взаимодействии для каждого из
элементов фрикционной связи [46]
()
()
()
2
3
22
3
11
3
5
1
3
2
1
3
2
3
4
1
22
3
8
11
3
2
2
3
2
2
3
2
1
3
2
1
3
4
1
3
4
1
3
22
3
11ch
3
1
1
1
3
4
1
3
4
1
2
ср1
3
2
3
2
1
1
69,093,31142,0
71,4
1
2473,8
4369,0
iii
ziizi
ii
ziiii
i
i
zizi
i
RRR
PRVP
RR
PRRR
R
R
PP
D
Γ+Γ
Γ+Γ
+
+
Γ+Γ
ΓΓ+Γ
+
+
−
Γ−
+Γ
=∆
ρ
ψ
τ
µ
τµ
(2.78)
()
()
()
2
3
22
3
11
3
5
2
3
2
2
3
2
3
4
2
22
3
8
22
3
2
2
3
2
2
3
2
1
3
2
1
3
2
2
3
2
2
3
2
1
3
2
1
3
22
3
11ch
3
1
2
2
3
4
2
3
4
2
2
ср2
3
2
3
2
2
2
69,093,31142,0
71,4
1
2473,8
4369,0
iii
ziizi
ii
ziiii
i
i
zizi
i
RRR
PRVP
RR
PRRRR
R
R
PP
D
Γ+Γ
Γ+Γ
+
+
Γ+Γ
ΨΓΓΓ+Γ
+
+
−
Γ−
+Γ
=∆
ρ
ψ
τ
µ
τµ
(2.79)

54
По зависимостям (2.78) и (2.79) определяется энергия в одном контакте,
которая затем суммируется по зависимости (2.77) и по количеству взаимодействий.
Энергия трения при пластическом взаимодействии поверхностей.
При работе реальных деталей часто возникает пластический контакт
между взаимодействующими неровностями поверхности. По Д. Муру [40] нормальная
нагрузка, действующая на поверхность:
∑∑
==
+=
2
1
1
1
m
mi
ii
m
i
i
APAPN
, (2.80)
где p
i
, p - давление на контакте и критическое давление соответствующее
началу пластического течения материала; A - фактическая площадь контакта; m
1
,m
2
-
число контактов.
После начала пластического течения рост давления на контакте прекращается,
увеличение нагрузки приводит к росту фактической площади контакта.
Энергия трения складывается из энергии внедрения и энергии сдвига, которые
определяются из выражения:
E
тр
= N h + S l σ
т
(2.81),
где h - относительное сближение; S - площадь сечения сдвигающейся массы; l -
путь трения.
2.4. Расчёт температуры контакта при трении.
Определением температуры поверхностей трения в той или иной степени
сталкивались представители всех современных теорий трения [9,24,30,43,65].
Подробные обзоры о возникновении и диссипации тепла при трении содержат
работы [24,30,46,65]. Однако приемлемой для инженерной практики методика
расчета температуры поверхности при трении в литературе нам не удалось
обнаружить.
Известно, что только элементы фактической площади контакта являются
источниками тепла трения [24].
В рамках сферической модели неровностей поверхностей [30] рассмотрим
образование и распределение тепла. Температура на фактической площади контакта
устанавливается в течение весьма коротких промежутков времени. Однако, для
стационарных (установившихся) тепловых процессов, когда их образование и
распределение не меняется во времени необходимо определенный промежуток
времени.
Для большинства инженерных задач, возникающих при проектировании
узлов трения характерно не изменяющиеся во времени нагрузка и скорость
скольжения, т.е. нагрузка на узел трения N и скорость скольжения v постоянные.
Такое ограничение, хотя приводит к некоторому частному рассмотрению задачи,
намного упрощает её решение.
Используя краевые условия, можно определить величину тепловых потоков,
идущих в контактирующие тела при действии теплового источника, возникающего
вследствие работы сил трения:
55
F
VNf
q ,q ,
21
112
221
2
1
⋅⋅
==+= qq
a
a
q
q
τλ
τλ
(2.82)
Время действия теплового источника
V
r2
=
τ
, (2.83)
где r - радиус пятна контакта; V - скорость скольжения.
Температура контактирующих тел в зависимости от времени действия
источника и расстояния от поверхности можно найти из следующих уравнений:
222111
22
11
2
11
22
1
2
24
exp2
τλτλ
τ
τπ
τ
τ
aa
a
z
erfc
z
a
z
a
aq
t
+
−
−
=
(2.84)
222111
22
22
2
22
11
2
2
24
exp2
τλτλ
τ
τπ
τ
τ
aa
a
z
erfc
z
a
z
a
aq
t
+
−
−
=
(2.85)
Ю.Н.Дроздов [9] для оценки температуры на единичном пятне
фактического касания пользуется формулами, полученными из решения тепловой
задачи с учетом работ Х.Блока и М.В.Коровчинского [24]. Приняв форму пятна
контакта в виде круга с радиусом r и с равномерно распределенной тепловой
интенсивностью q = f p
ср
v, что вполне приемлемо как по распределению напряжений и
скоростей, так и для решения тепловой задачи получает следующие зависимости [9]:
1
1
λ
ϑ
rq
=
(Pe = 0) неподвижный тепловой источник;
πλ
ϑ
1
1
2 rq
=
(Pe < 0,3) малая скорость движения источника;
Pe
rq
πλ
ϑ
1
1
22
=
(Pe > 8) большая скорость движения источника,
здесь q
1
- тепловой источник, идущий в теле 1 и Pe = 2r
1
υ /Q - относится к телу 1.
Температура вспышки согласно [9] будет равна сумме температур тела 1 и 2, т. е.
q = q
1
+ q
2
. Например,
56
()
2211
21
22
PePe
qr
λλπ
ϑϑ
+
=+
(2.86)
Температура на площади кругового контакта по Х.Блоку [71]:
Φ
+
Φ
+
=
2
2
1
12
2
2
1
22
2
π
λ
λ
ρ
C
fP
T
(2.87)
Ю.Н.Дроздов [8], приводит уравнение для температуры контакта
()
()
2
3
4
τπρ
τ
aFc
q
T =
, (2.88)
где τ - время; Q - количество тепла, выделяемое в контакте; C - теплоёмкость
материала; ρ - плотность материала; F - площадь фактического пятна касания; a = λ/ρC
- коэффициент температуропроводности. Эту формулу можно рассматривать как
случай охлаждения точки поверхности полубесконечного тела после получения ею
количества тепла Q.
63
Глава 3. ПРИРАБОТКА УЗЛОВ ТРЕНИЯ МАШИН.
3.1. Изменение шероховатости поверхностей
во время приработки
.
Известно, что качество проведения обкатки после сборки
влияет на надежность машин. Во время обкатки выявляются
технологические дефекты, поверхности трения прирабатываются на
микро- и макроуровнях. Экспериментально установлено, что в
процессе трения устанавливается равновесная шероховатость,
отличающаяся от первоначальной. Значение равновесной
шероховатости зависит от приложенной узлу трения нагрузки,
скорости скольжения и свойств материалов пары трения [11].
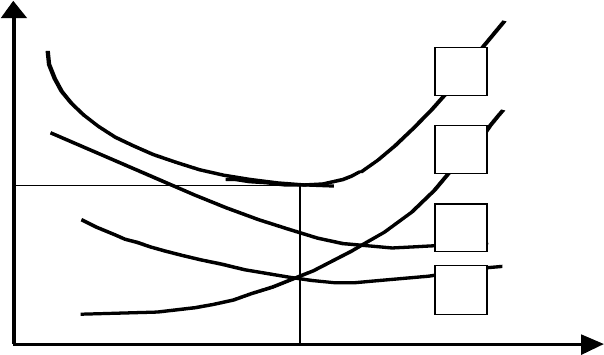
Поверхность изменяет свою шероховатость до достижения
минимума коэффициента трения, что соответствует минимальной
энергии трения (рис.9).
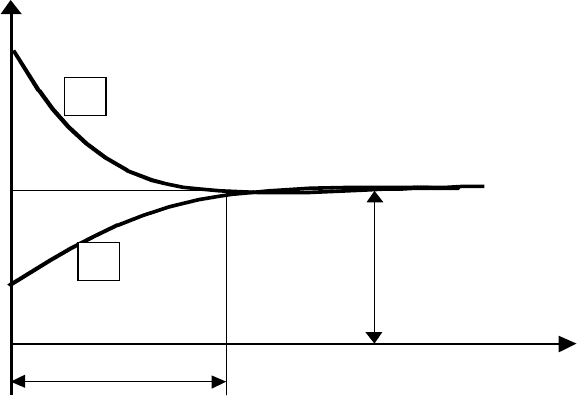
При приработке исходная шероховатость претерпевает
значительные изменения и, независимо от исходной
шероховатости, устанавливается своя равновесная шероховатость,
параметры которой зависят от режимов приработки и условий
смазки. Исходная шероховатость в основном влияет на время
приработки (рис. 10.) [23,74].
f
f
min
R
a равновесная
R
a
,мм
1
3
2
4
Рис. 9. Зависимость коэффициента трения от шероховатости.
1 - адгезия при сухом трении; 2 - механическое взаимодействие;
3 - полный коэффициент трения; 4 - адгезия при граничном трении.
64
R
a
Мкм
R эксплуатационная
Прирабо тка Время, час
1
2
Рис. 10. Изменение шероховатости поверхности от
продолжительности трения.
1 - при преобладающем механическом взаимодействии;
2 - при преобладающем адгезионном взаимодействии.
Технологическая шероховатость (шероховатость, полученная
путем обработки поверхности во время изготовления) влияет на
длительность приработки. Равновесная шероховатость может
служит показателем конца приработки. Ускорение приработки путем
ужесточения режимов (форсирование по нагрузке, холодная
обкатка и т.п.) не дает хороших результатов потому, что всегда это
связано с отклонениями от реальных условий эксплуатации.
Таким образом, к концу приработки необходимо выйти к тем
режимам, на которые рассчитана длительная эксплуатация узла
трения.
Для лучшей микрогеометрической приработки желательно,
чтобы после механической обработки шероховатость поверхности
деталей была бы близко к оптимальной. В этом случае процесс
приработки будет менее продолжительным, а износ при приработке
- минимальным. Если шероховатость поверхностей перед
приработкой слишком велика, то при приработке возникают
большие удельные давления в точках фактического контакта, и
возможно появление задиров и преждевременный износ
сопряжения. С другой стороны, слишком малая шероховатость
связана с затратой излишней трудоёмкости в процессе
механической обработки поверхностей деталей.
Поверхности трения, которые образованы по специальным
микрорельефам (например выбронакатка) могут успешно работать
65
только в тех условиях, когда предельный износ меньше или равно
приработочному износу. Проведение обкатки таких деталей не
имеет смысла. Заводская приработка, проведенная в условиях
отличных от эксплуатационных, не только бесполезно. но и вредно,
т.к. при других режимах снова происходит приработка более
длительное время и с большой величиной износа.
Соотношения между механическим и адгезионным
составляющими коэффициента трения определяет образование
шероховатости поверхности с определенными геометрическими
характеристиками при установившемся трении. Вероятно,
механическая составляющая коэффициента трения приведет к
уменьшению шероховатости по мере изнашивания наиболее
высоких выступов. Если поверхности гладкие, то сила адгезии
между ними велика и вырыв частей материала из-за сильных
адгезионных связей приводит к росту шероховатости поверхности.
С увеличением высоты неровностей механическое
взаимодействие увеличивается, а адгезия уменьшается. Наличие
смазки между поверхностями трения препятствует сближению
поверхностей на уровне действия радиуса молекулярных сил, что
сказывается в уменьшении адгезии (рис. 9).
При одинаковых R износ может быть разным. Полученные
различными видами обработки поверхности (выглаживание,
шлифование, полирование, притирка, хонингование) хотя могут
иметь одинаковые значения R , отличаются структурой материала
профиля и изнашиваются на различные величины [64].
Прогнозирование параметров равновесной шероховатости на
стадии проектирования деталей машин сдерживается
отсутствием достоверных методик расчета, удовлетворяющих
требования проектно- конструкторских организаций.
В работе [29] предложена зависимость для расчета параметров
равновесной шероховатости.
5
1
5
2
в
5
4
4
3
2
4
5
г
0
2,0
1
16
2
−
=
a
в
a
A
N
R
Н
Е
Е
R
µ
α
τ
, (3.1)
где α
г
- коэффициент гистерезисных потерь; τ
0
- сдвиговая
прочность молекулярных связей; H
в
,R
в
- высота и радиус волн.

66
Несмотря на очевидную полезность попытки сделанной
авторами попытки расчёт носит приближенный характер. Так,
вместо параметров шероховатости "b" и "ν " здесь определяется
обобщенный параметр "∆", косвенно связанный с истинными
показателями шероховатости по ГОСТ 2789-73. Практическое
использование указанной методики расчёта затруднено ещё и тем,
что входящий в расчётные зависимости значение сдвиговой
прочности молекулярных связей в каждом конкретном случае
приходится определять экспериментально.
Представляет трудность также определение значений
коэффициента гистерезисных потерь экспериментальным путём.
3.2. Расчет характеристик микрогеометрии поверхностей.
В процессе приработки шероховатость непрерывно меняется.
Поэтому при рассмотрении процесса приработки должно
учитываться изменение радиусов кривизны вершин выступов.
Исходные параметры шероховатости поверхностей
определяются из профилограммы. Для определения характеристик
микрогеометрии выбирают несколько участков (не менее пяти),
наиболее характерных для исследуемой поверхности, с которых
снимается профилограммы. Длина исследуемого профиля участка
должна быть менее базовой длины.
Среднее арифметическое отклонение профиля R
а
отсчитывают непосредственно по шкале профилографа-
профилометра. Среднее арифметическое отклонение профиля R
имеет следующее геометрическое значение:
()
∫
∑
=
==
l
n
i
i
Y
n
dxxY
l
R
0
1
11
, (3.2)
где l - базовая длина.
Для определения среднего арифметического отклонения
профиля строят среднюю линию в каждых участках
профилограммы. Для этого от горизонтальной линии, проведенной
параллельно профилю ниже самой глубокой впадины профиля,
замеряют ординаты профиля Y
1
,Y
2
,Y
3
... Y
n
через каждый
интервал. Все полученные значения разбивают на две равные
половины для левой и правой частей профилограмм (Y
1
– Y
n/2
и Y
n/2
– Y
n
). среднюю линию проводят через точки с координатами X
’
,Y
’
и
X
’’
, Y
’’
:
