Махкамов К.Х. Расчет износостойкости машин: учебное пособие
Подождите немного. Документ загружается.

41
Из выражения (2.30) путем интегрирования можно получить
продолжительность нагрева рабочей поверхности
∫
−Φ
−
Φ
=
−Φ
=
At
At
A
C
At
Cdt
T
T
T
0
ln
τ
(2.31),
где t
0
- начальная температура рабочей поверхности детали.
Введем обозначение C/A = T. Тогда из (2.31) получим закономерность
изменения средней температуры трущихся поверхностей деталей [14]
tt
T
ete
A
t
ττ
−−
+
−
Φ
=
0
1
(2.32)
При τ → ∞ , t
max
= Ф
T
/A . Тогда
TT
etett
ττ
−−
+
−=
0max
1
; (2.33)
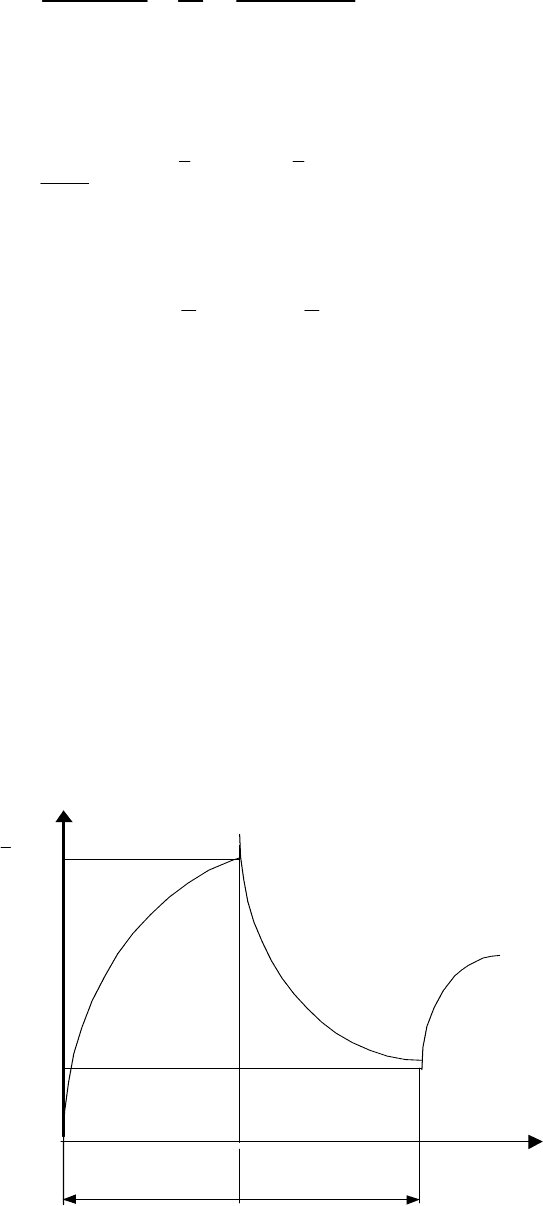
т.е. закономерность увеличения температуры рабочих поверхностей деталей при
трении описывается экспоненциальной зависимостью (рис. 5).
Б.И.Костецкий и Ю.И.Линник [26] изучали энергетический баланс при трении
методом калориметрирования. Результаты исследований показали, что значительная
часть энергии в процессе трения превращается в тепловую (таблица 3). Режимы
испытаний были следующими: P = 0,6 МПа, v = 0,34 м/с, L = 1000 м, среда -
вазелиновое масло, поверхности 13 - 14 классов шероховатости, погрешности
измерений 1,9 %.
Исследование энергобаланса в реальных условиях трения связано с серьезными
трудностями и, в первую очередь, с необходимостью обеспечения сложного
эксперимента, позволяющего получать достоверные результаты. Поэтому при
решении ряда неотложных вопросов эмпирический путь исследования становится
предпочтительней как более оперативно обеспечивающий решение требуемой частной
задачи [70].
t
t
max
t
1
t
0
τ
τ
1
нагрев t
ц
τ
2
охлажден ие
Рис. 5. Изменение температуры рабочей поверхности
детали при трении.
42
Б.В.Протасов разделяет трансформационный процесс превращения механической
энергии в другие виды во время трения на два этапа [46]. На первом этапе
генерируется поток, состоящий из:
- энергии, затрачиваемой на деформирование поверхностей;
- энергии, затрачиваемой на преодоление молекулярного взаимодействия
трущихся тел;
- энергии инерции и колебания. На втором этапе этот поток энергии
рассеивается за счет:
- роста внутренней энергии материала;
- тепла, рассеиваемого в окружающую среду;
- энергии разрушения и диспергирования.
Энергия, затрачиваемая на каждый контакт (генерируемый поток)
[
]
[
]
[
]
и
2
и
1
м
2
м
1
мах
2
мах
1
A WWWW ∆+∆+∆+∆+∆Π+∆Π=
(2.34).
Эта формула показывает, сколько энергии трения может преобразоваться на
каждом контакте.
Энергия, затраченная на каждом контакте (рассеиваемый поток)
[
]
[
]
[
]
д
2
д
121
в
2
в
1
A WWQQWW ∆+∆+∆+∆+∆+∆=
(2.35),
где ∆W
в
- приращение внутренней энергии, ∆Q - тепло, ∆W
д
- энергия
диспергирования (разрушения). Отсюда определятся, сколько энергии может
расходоваться на каждом контакте.
Таблица 3.
Энергетический баланс при трении металлов
п/п
Пара трения Работа внешних
сил, А кДж/см
Тепло Q% Поглощенная энергия
∆E, % ∆E, Дж/см
АмцМ-АмцМ 1,26 93 7 92
Cu - Cu 2 96 4 82
Fe - Fe 2,15 97,5 2,5 53
Ст.45-Ст.45 2,6 98,5 1,5 41,5
Ст.45-Ст.45
закаленные
2,36 100 0 0
Поскольку энергия превращается из одного вида в другой, согласно закона
сохранения энергии можем написать для каждого контакта
[
]
[
]
[
]
[][][]
д
2
д
121
в
2
в
1
и
2
и
1
м
2
м
1
мах
2
мах
1
WWQQWW
WWWW
∆+∆+∆+∆+∆+∆
=∆+∆+∆+∆+∆Π+∆Π
(2.36)
Если левая часть этого уравнения даёт нам энергию трения E
тр
, то правая часть
показывает её расход на рост внутренней энергии материала, на тепло и на энергию
разрушения.
В зависимости от условий энергия, преобразованная (трансформированная) в
процессе трения, может расходоваться по-разному на окисление смазки,
распространяется в окружающую среду в виде тепла и т.п. Поэтому при анализе
43
энергетического баланса необходимо использовать не только максимальные величины
распределения, а конкретные значения его составляющих.
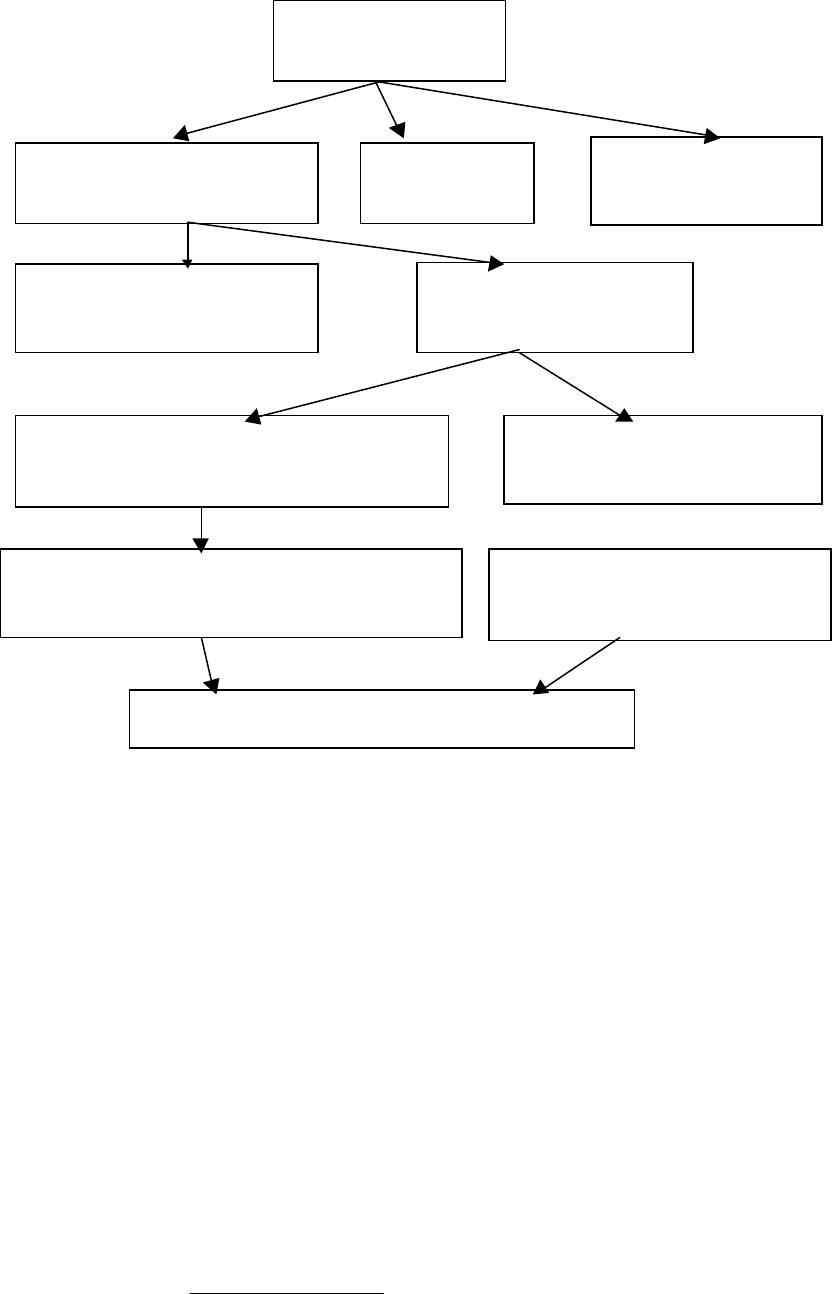
Распределение энергии с точки зрения необратимых неравновесных
термодинамических процессов рассмотрено В.В.Федоровым [58] (рис.6).
Поверхности трения изнашиваются в результате взаимодействия. Процесс
изнашивания сопровождается энерго - обменом между узлом трения и окружающей
средой. Энергия трения частично поглощается материалом (активация) и частично
передаётся в окружающую среду (пассивация) в виде теплового потока.
Если плотность энергии в микрообъёме материала достигнет критического
значения E, происходит разрушение (изнашивание) этого объема. Критическая
энергоёмкость материала величина постоянная [58]. Для каждого материала имеется
своя критическая энергия, при достижении которой образуется частица износа.
Критическая плотность энергии показывает, сколько скрытой энергии может
накопиться в единице объема материала до наступления разрушения (для преодоления
сил связи в кристаллической решетке). Энергетическое состояние материала
характеризуется показателем E
м
V
д
.
Плотность скрытой энергии материала можно представить в виде
E
м
= E
0
+ ∆E (2.37),
где E
0
- исходная плотность внутренней энергии материала; E
м
- изменение
плотности внутренней энергии, т.е. сколько энергии подведено данному объёму
материала извне.
44
Работа трения
E
тр
=
∆
E + Q
Работа деформации Тепловая Электрическая
материала E
д
энергия Q энергия E
эл
Изменение скрытой Тепловой эффект
энергии
∆
U
е
деформации q
Изменение тепловой энергии Энергия теплообмена
материала
∆
U
т
q
→
Изменение внутренней энергии Внутренняя энергия в
∆
E =
∆
U
е
+
∆
U
т
исходном состоянии U
0
Внутренняя энергия U= U
0
+
∆
E
Рис. 6. Схема энергетического баланса процессов
трения и изнашивания [58].
Поскольку изнашивается энергонасышенный объём материала, то, очевидно
выражение E
*
V
изн
показывает фактически затраченную энергию на изнашивание.
Тогда, условия изнашивания можно написать так
E
*
V
изн
= E
м
V
д
(2.38),
где E
*
- критическая плотность внутренней энергии; V
изн
- объём изношенного
материала (продуктов изнашивания); V
д
- объём материала, подвергавшиеся
энергетическим изменениям.
Основываясь на механическую модель фрикционного взаимодействия
шероховатых поверхностей, получены уравнения, позволяющие определить объём
материала, участвующего в упругих и пластических деформациях [53]. Эти уравнения
можно использовать для ориентировочных расчетов, допуская, что энергетическим
изменениям подвергается деформируемый объём материала. Отсюда имеем:
∗
⋅∆+
=
Е
VЕЕ
V
д0
изн
)(
(2.39).

45
По В.В.Федорову [58] формула для расчёта объёмного износа в принятых
нами обозначениях имеет вид
)(
изн
QЕ
Е
V
−
∆
=
∗
(2.40),
где Q - тепловая энергия; ∆E - изменение скрытой энергии.
По Г.Фляйшеру [59,60] эта же формула имеет вид
V
изн
= E
тр
/ E
*
, J = τ V
изн
/E
тр
, E
тр
= A
а
L τ (2.41),
где E
тр
- энергия трения.
Если В.В.Федоров считает, что теплоотвод изменяет критическую
энергоёмкость материала, то Г.Фляйшер попросту не учитывает рассеивание теплоты,
образуемой в процессе трения.
При деформации реальных материалов, содержащих дефекты, суммарная
величина удельной энергии, поглощаемой деформируемым объёмом до разрушения,
зависит не только от сил межатомных связей, но и от энергии, имеющейся в металле
до деформации, величина которой определяется исходным структурным состоянием,
а также условиями нагружения, влияющими на степень неоднородности насыщения
энергией отдельных объёмов металла при деформации [57].
Исходная плотность внутренней энергии по существу является механической
энергией, аккумулированной в металле в форме остаточных напряжений [8].
()
(
)
E
E
6
321
2
0
σµ
−
=
, (2.42)
где µ - коэффициент Пуассона; E - модуль упругости (Юнга); σ - остаточные
напряжения.
Напряженное состояние материала может служить показателем его
внутренней энергии. Внутренние напряжения, возникающие в поверхностном слое
материала вследствие тепловых процессов [14]
σ = 0,5 (t
2
- t
1
) α E, (2.43),
где t
1
, t
2
- исходная и максимальная температуры поверхностного слоя; α-
коэффициент линейного расширения материала детали; E - модуль упругости
материала, соответствующий температуре нагрева поверхностного слоя.
Изменение напряжений с истечением времени по Максуэллу
−⋅=
µ
σσ
ET
i
exp
(2.44),
где σ - начальное напряжение; µ - вязкость металла; E - модуль Юнга; T - время.
Здесь начальное напряжение определяется, исходя из метода обработки. Например,
при резании сила резания делится на площадь резания и т.п.
Определение исходного энергетического состояния обработанных различными
технологическими приёмами поверхностей представляет отдельную самостоятельную
задачу.
2.3. Расчет энергии сил трения при взаимодействии
поверхностей.
Обоснование расчётной модели.
46
Существуют два способа определения энергии трения. Первый способ
применяется, когда известно значение коэффициента трения.
E = N f L = N f v t , (2.45),
где L - путь трения; N - нормальная нагрузка; f - коэффициент трения; v -
скорость скольжения; t - время.
Учитывая характер фрикционного взаимодействия деталей сопряжения, можно
определить коэффициент трения по зависимости, предложенной И.В.Крагельским [29]
f= τ
0
/HB + β + k а
н
(h/R)
1/2
, (2.46)
где τ
0
и β - параметры, характеризующие сопротивление сдвигу и сил
молекулярного взаимодействия поверхностей; HB - твердость поверхности по
Бринелю; k - коэффициент, учитывающий форму неровностей и распределение их по
высоте; а
н
- коэффициент гистерезисных потерь; h/R - относительное внедрение
единичной неровности.
Определить точно коэффициент трения, используя выражение (2.46), не
представляется возможным вследствие слабой изученности процесса силового
взаимодействия твердых тел при упругопластических деформациях материала в зонах
контакта, что не позволяет с достаточной точностью установить величину внедрения
неровностей трущихся поверхностей [14].
Коэффициент трения в условиях граничной смазки представляет собой
сумму трёх слагаемых [14]
f
r
= f
т
+ f
ж
+ f
пр
, (2.47),
где f
т
, f
ж
, f
пр
- составляющие коэффициента трения, обусловленные
соответственно механическим воздействием твердых поверхностей, внутренним
трением слоев смазочного материала и сопротивлением трения, вследствие
пропахивания поверхности выступами неровностей при повреждении смазочной
пленки.
f
r
= ασ
тв
/p + (1-α) σ
ж
/p + f
пр
(2.48)
где α - доля номинальной площади, на которой происходит механическое
взаимодействие рабочих поверхностей деталей;
σ
тв
- прочность на срез твердого
материала детали; σ
ж
- сопротивление относительному перемещению слоев смазочного
материала; p -среднее номинальное давление в зоне контакта.
Поскольку существует первоначальная и установившаяся равновесная
шероховатость, то следует, ожидать, что существует и установившийся коэффициент
трения. В общем случае коэффициент трения очень чувствителен к изменению
условий трения, поэтому расчет энергии трения через коэффициент трения может
быть использован только для ориентировочных расчётов.
Известно, что КПД различных методов преобразования энергии
определяются из выражения
η= W/E , (2.49)
где W - совершаемая работа; E - затрачиваемая энергия.
Поскольку трение является процессом преобразования механической
энергии в тепловую и электрическую, то вышеуказанное выражение может быть
использовано для оценки КПД преобразования энергии при трении. Здесь в роли
47
совершаемой работы выступают механические, физико-химические и энергетические
изменения в поверхностных слоях материалов пары трения, а затрачиваемая энергия
равна потери энергии системой в процессе трения. Под системой понимаем машину,
узел, агрегат, пары трения и тому подобное, где имеется возможность замерять
энергию при входе и выходе.
Называя в дальнейшем КПД коэффициентом энергетических потерь,
физический смысл которого заключается в том, что здесь показывается, какая часть
механической энергии преобразуется в другие виды энергии, получим:
η = ∆E /(N
вход
–N
выход
) (2.50).
Б.В.Протасов [46], рассматривая упругий контакт сферических
неровностей, получил выражение для расчета энергии трения. Однако в полученных
расчетных зависимостях допущены математические погрешности, влияющие на
точность конечных результатов. Кроме того, в работе [46] не рассмотрен
пластический контакт неровностей поверхности деталей, который наиболее часто
появляется в реальных машинах и механизмах.
Следуя работе [46], рассмотрим взаимодействие шероховатых поверхностей,
моделированных сферами. Сначала рассматриваем упрощенную модель, когда
скорость скольжения, нагрузка и внешняя среда постоянные.
Трущиеся смазываемые поверхности представляют собой систему
"материал-среда-материал". Обычно трение, если систему отсчёта будем брать в одной
из трущихся поверхностей, можно заменить относительным скольжением элементов
сопряжения между собой.
Тогда одна из поверхностей условно будет считаться неподвижной, а другая -
подвижной. Характер движения подвижной поверхности относительно неподвижной
может быть вращательным, поступательным или сложным, равномерным или
ускоренным, а также колебательным. Если рассматривать вышеуказанную систему в
достаточно малый промежуток времени и на достаточно малом участке, то
независимо от характера взаимного перемещения поверхностей трения можно
утверждать, что в каждый данный момент поверхность 1 движется относительно
поверхности 2 поступательно с мгновенной линейной скоростью v [16].
Реальные поверхности трения состоят из множества вершин и впадин,
подчиняющихся определенному закону распределения. Распределение высот
неровностей профиля обычно подчиняются нормальному закону. Допущение
нормальности справедливо для большинства механически обработанных поверхностей
[40]. Для математического описания модели поверхности используются следующие
параметры шероховатости: высота неровностей, их форма и шаг неровностей. Обычно
форму неровностей моделируют сферами радиусом R.
И.В.Крагельский [30] предлагает моделировать шероховатую поверхность
набором сферических сегментов. Сферы имеют одинаковый радиус R
в
, равный
среднему радиусу кривизны микронеровностей реальной поверхности. Для
определения радиуса единичного выступа предлагается формула:
R
в
= 1/(π
2
R
a
λ
2
), (2.51),
где λ - среднее число пересечений профилем средней линии на единицу длины.
Эту хорошо зарекомендовавшую себя модель, предложенную
И.В.Крагельским, используем в дальнейшей работе.
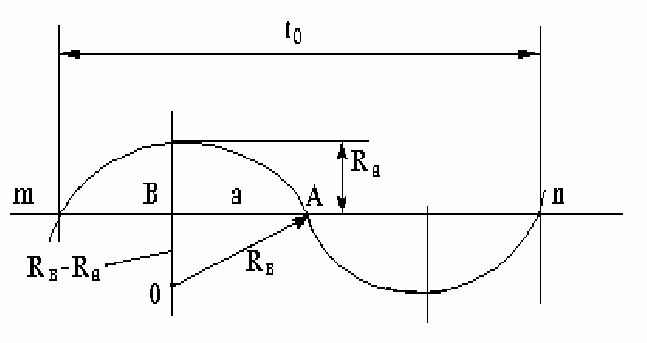
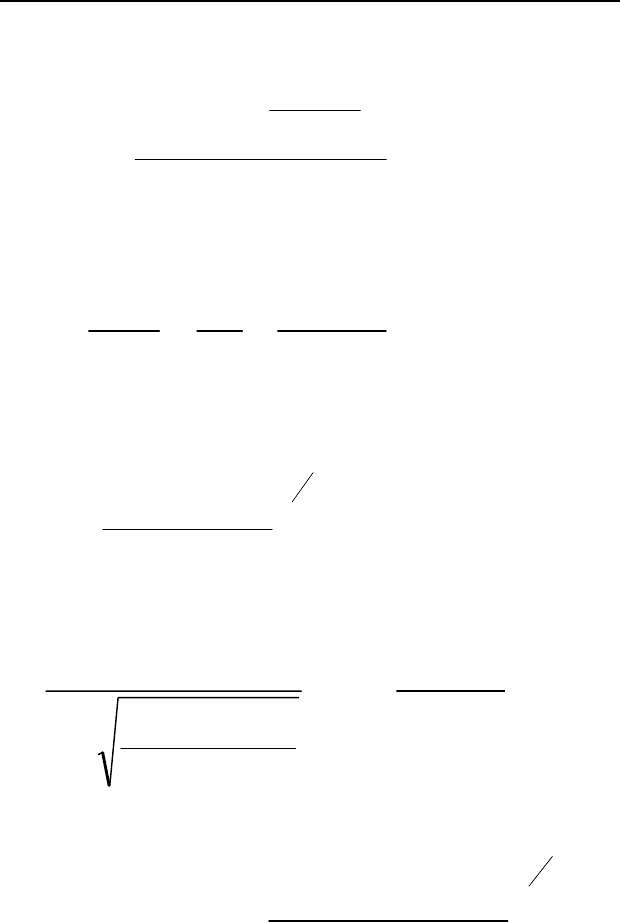
Для исследования связи среднего радиуса неровности и средней высоты
используем теорему Пифагора (рис.7). Из треугольника ОВА имеем:
48
а
2
= R
b
2
- (R
b
- R
a
)
2
, (2.52),
где a - радиус основания выступа. Принимая шаг неровности t
0
=4a, получим:
R
b
= (t
0
2
+ 16 R
a
2
)/32 R
a
(2.53).
При моделировании шероховатых поверхностей трения необходимо учесть
направление штрихов окончательной обработки деталей. В общем случае
шероховатость поверхности различна в разных направлениях. Если направление
движения относительного скольжения поверхностей перпендикулярно замеренной
шероховатости, то шероховатость в направлении движения может быть вычислена
[49].
Необходимо отметить, что в процессе изнашивания шероховатость меняется.
Исходная шероховатость, полученная путем механической или другой
технологической обработки, в период приработки принимает другие значения. Во
время нормального изнашивания поверхность трения будет иметь равновесную
шероховатость.
Поэтому при расчете износостойкости конкретных деталей машин
необходимо пользоваться установившимся значением шероховатости. Этим
обуславливается изучение процесса приработки поверхностей как самостоятельной
задачи.
Поверхности трения реальных деталей имеют погрешности изготовления,
объединенные в три класса - макроотклонения формы, волнистость и шероховатость.
При изучении механизма взаимодействия поверхностей трения достаточно
учитывать только их шероховатость. Макро- геометрические отклонения формируют
форму зазора и должны учитываться при расчете влияния износа на
работоспособность сопряжения. Вследствие того, что механизм изнашивания
рассматривается на достаточно малом участке, то значением макро-отклонений
детали здесь можно пренебречь.
Рис. 7. Схема к расчету среднего радиуса выступа.
Волнистость поверхности также моделируется чередующимися сферами.
Необходимо различать поперечную и продольную волнистость. Волнистость
поверхности необходимо учитывать при расчете фактической и контурной площадей
контакта поверхностей.
Обычно машины в Центральной Азии работают в тяжелых эксплуатационных
условиях при присутствии абразивных частиц. Результаты исследований [16,31]
показали, что абразивной частице присуще округлая форма и даже твердые и прочные
49
частицы корунда и карборунда имеют на поверхности значительные закругления, а
абразивные частицы кварцевого происхождения имеют ещё больший радиус
округления. Исходя из вышеизложенного, абразивную частицу принимаем округлой
формы, имеющей несколько радиусов. Частицы такой формы обладают более высокой
механической прочностью, чем остроугольные. Для упрощения расчетных
зависимостей возможно использование сферической модели частицы в виде шара,
являющейся частным случаем модели нескольких радиусов.
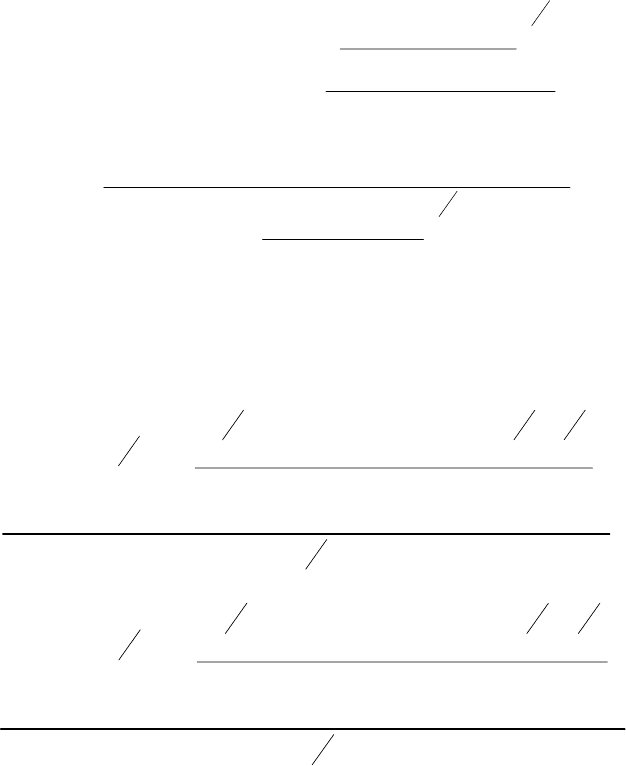
Энергия трения при упругом взаимодействии поверхностей.
Потенциальная энергия упругой деформации сферического сегмента при
действии сил P
z
и P
x
(рис. 8)
2
P C
P C
2
xx
2
zz
+
=∆Π
z
С
(2.54),
где C
z
, C
x
- податливость в направлениях z и x.
По Миндлину [72] для упругих деформаций
()
µ
µµ
−
−
=
−
=
12
2
C
C
;
2
1
z
x
aG
C
(2.55),
где µ - коэффициент Пуассона; G - модуль сдвига; a - полуось пятна контакта.
Полуось пятна контакта полусферы с твердой поверхностью определяется по
формуле Герца:
(
)
3
1
2
2
13
−
=
E
RP
a
z
µ
(2.56).
Подставляя (2.60) и (2.61) в (2.59), получим:
()
()
−
−
+
−
−
=∆Π
22
3
2
12
2
2
13
4
1
xz
z
PP
E
RP
G
µ
µ
µ
µ
(2.57).
Максимальное значение сдвигающей силы равно:
()
3
1
2
1
2
1
2
22
ср
2
1
max
4
19
−
==
E
RP
aP
izi
cpixi
µ
πττπ
(2.58).
Максимальное значение силы P определяется из условия среза адгезионной
связи по меньшему пятну контакта. Поэтому рассчитываем P
x1
и P
x2
, сравниваем их и
меньшее из них принимаем за P
xi
max
.
При контакте шероховатых поверхностей выступы более твердой поверхности
внедряются в менее твердую поверхность, и основное значение приобретает
"пропахивание" - образование дорожек трения на менее твердой поверхности. Сила
трения определяется в основном прочностью на сдвиг (срез) менее твердого материала
50
пары трения и площадью сдвига, развивающейся при трении. На поверхности трения,
покрытой прочно удерживающейся пленкой с низкой прочностью на срез, сдвиг при
трении происходит не в твердом металлическом подложке, а в мягком материале
пленки [11].
В условиях граничной смазки полная сила трения F будет равна сумме сил,
необходимых для производства сдвига по площади S в материале пленки и для
оттеснения металла образца по площади S
n
при образовании дорожки трения
F = S τ
пл
+ S
n
Q (2.59),
где Q - сопротивление материала пластическому оттеснению (предел текучести
материала); S - площадь трения; S
n
-площадь поперечного сечения дорожки трения; τ
пл
- прочность на срез материала пленки.
Полная потенциальная энергия
()
()
(
)
()
()
3
1
1
1
2
1
1
2
1
4
1
4
1
2
1
4
22
1
2
1
2
13
4
12
16
181
2
1
µ−
µ−
µ−
τπµ−+
µ−=∆Π
E
RP
G
E
RP
P
izi
izi
срzi
max
i
(2.60).
Поскольку модуль сдвига G, коэффициент Пуассона µ и модуль нормальной
упругости E связаны соотношением G = E / 2(1- µ), то из (2.60), обозначая Г = (1 -
µ
2
)/E, получим
()
()
3
1
1
1
3
4
1
3
4
1
2
1
3
2
3
2
1
max
1
1
2473,8
4369,0
i
iсрzi
zi
R
RP
P
−
Γ−+
Γ
=∆Π
µ
τµ
(2.61)
()
()
3
1
2
2
3
4
1
3
4
2
2
2
3
2
3
2
2
max
2
1
2473,8
4369,0
i
iсрzi
zi
R
RP
P
−
Γ−+
Γ
=∆Π
µ
τµ
(2.62).
Энергия скольжения пятна контакта в молекулярном взаимодействии:
(
)
21
maxм
aaPW
xi
+=∆
, (2.63),
