Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


MWD and LWD
915
Figure
4-230.
Photograph
of
a high-temperature directional sensor with three
accelerometers and three magnetometers.
(Courtesy
Develco
[I
031.)
The tool face angles are counted looking downward, clockwise positive and
counterclockwise negative.
We will assume a perfect accelerometer calibration line that reads
3
mA
for
1
g of acceleration.
Solution
Tables
4-118
and
4-119
give answers to Example
1
in tabular form.
Example
2:
Steering
Tool
Measurements-Tool Face, Deviation, and Azimuth
The following set of data have been recorded with a
MWD
directional package:
Gx
=
-0.2
mA
GY
=
0.1
mA
Gz
=
2.99 mA
Accelerometer sensitivity:
3
mA
=
1
g
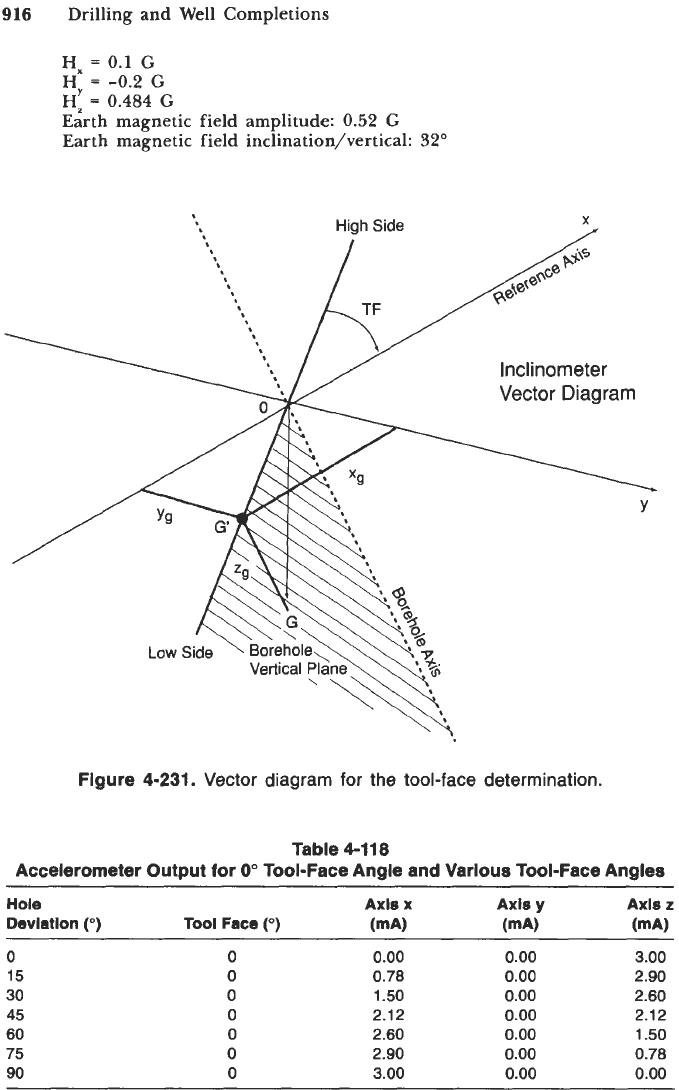
916
Drilling and Well Completions
Hx
=
0.1
G
Hz
=
0.484
G
Earth magnetic field amplitude:
0.52
G
Earth magnetic field inclination/vertical:
32"
HY
=
-0.2
G
High
Side
I
Figure 4-231. Vector diagram for the tool-face determination.
Table 4-118
Accelerometer Output for
0"
Tool-Face Angle and Various Tool-Face Angles
Hole
AXIS
x
Axis
y
Axis
z
Devlation
(")
Tool
Face
(")
(mA) (mA) (mA)
0 0
0.00
0.00
3.00
15
0
0.78
0.00
2.90
30
0
1.50
0.00
2.60
45
0
2.12
0.00
2.12
60
0
2.60
0.00
1.50
75
0
2.90
0.00
0.78
90
0
3.00
0.00
0.00

MWD and LWD
917
Table
4-119
Accelerometer Output for
30"
of
Hole Deviation
Angle and Various Tool-Face Angles
Hole
Axis
x
Axis
y
Axis
z
Deviation
(")
Tool
Face
(")
(mA) (mA) (mA)
30
30
30
30
30
30
30
30
30
-1
80
-1
35
-90
-45
0
45
90
135
180
-1.50
-1.06
0.00
1.06
1.50
1.06
0.00
-1.06
-1.50
0.00
-1.06
-1.50
-1.06
0.00
1.06
1.50
1.06
0.00
2.60
2.60
2.60
2.60
2.60
2.60
2.60
2.60
2.60
1.
Compute the inclination of the borehole. Are the accelerometers working
2.
Compute the tool face angle, clockwise and counterclockwise. If we drill
3.
Compute the field disturbance
Hdc
due to the drill collars.
4.
Compute the inclination
of
the corrected magnetic field. Does it check with
the local data? What could prevent this inclination from being correct?
5.
Give the principle of one of the borehole azimuth calculation methods.
properly? Why?
ahead with this angle is the hole going to turn left or right?
Solution
1.
The inclination is i
=
4.27".
Yes, the accelerometers work properly because
2.
The tool-face angle is TF
=
26.56'.
The borehole is turning right.
3.
Hz
=
0.469
G,
H,,
=
0.014
G.
4.
Corrected field inclination:
25.69".
External disturbance: nearby casing or
5.
If
Z
is the borehole axis unit vector,
drill collar hot spots.
compute
A
=
G
x
Z
(vector product)
and
B=GxH
AaB
cosa
=
-
1-41
PI
(scalar product)
Example
3:
Steering Tool Measurements-Tool Face,
Deviation, and Azimuth
A
steering tool is normally used during drilling with a mud motor and is
connected to the surface with an electric wireline. The sensing devices shown
in Figure
4-232
are also used in most MWD mud pulse systems. The coordinates
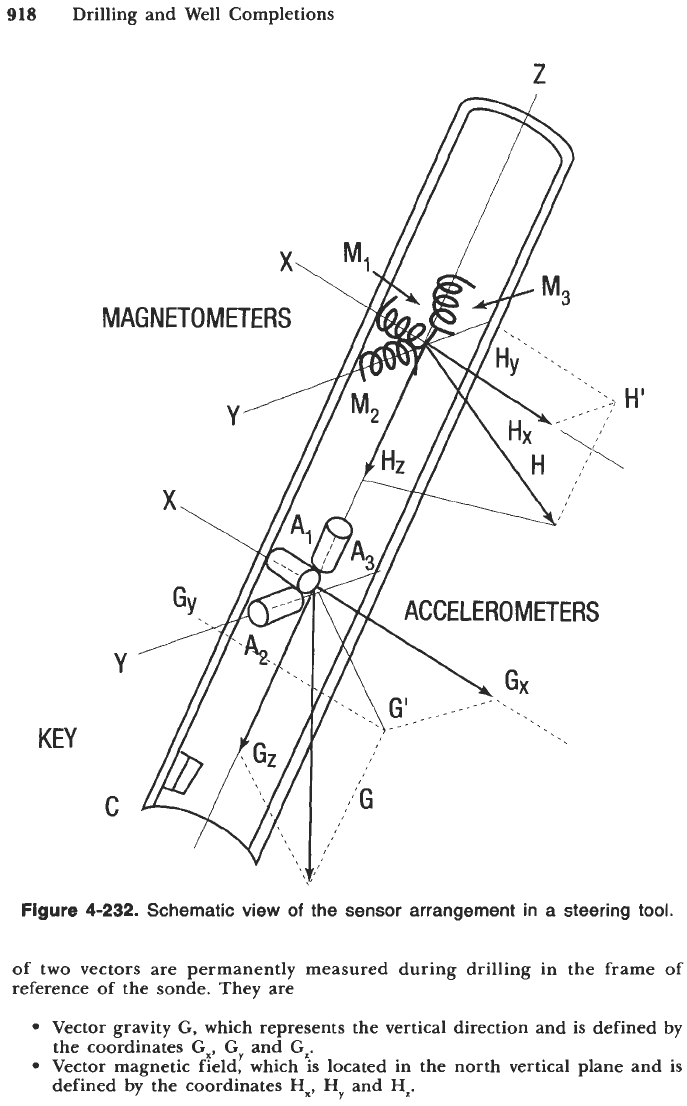
918
Drilling and Well Completions
Z
H'
KEY
Figure
4-232.
Schematic view
of
the sensor arrangement in a steering tool.
of two vectors are permanently measured during drilling in the frame of
reference of the sonde. They are
Vector gravity
G,
which represents the vertical direction and is defined by
the coordinates
Gx,
CY
and
GI.
Vector magnetic field, which is located in the north vertical plane and is
defined by the coordinates
Hx,
HY
and
HI.

MWD and LWD
919
Also needed:
Vector well direction located along the well (sonde axis) and is defined by
the coordinates
Zx
=
0,
Zy
=
0
and
Zz
=
1.
Ox
is lined up with the mule shoe key and the tool face direction.
For the numerical applications, we shall have:
Accelerometer scale factor
3
mA/g, Ix
=
-2
mA, Iy
=
1
mA, IT
=
2
mA at a
given depth,
Magnetometer readings:
Hx
=
-0.1077
G,
HY
=
0.2
G,
Hz
=
0.45
G
at the
same depth,
Magnitude of the magnetic field:
0.52
G,
magnetic field inclination:
30"
with respect to the vertical.
1.
Compute the borehole deviation. Show that a check of the accelerometer
readings is possible if we assume that the
G
vector module is g.
2.
Compute the tool face orientation. In the numerical application above, is
the borehole going to turn right, left or go straight
if
we keep on drilling
with this orientation?
3.
Show that we can check the magnitude of the magnetic field vector and
correct for an axial field due to the drill collars.
4. Compute the dip angle of the magnetic field vector after correction for
the drill collar field, it should check with the local magnetic field data.
What do you conclude if it does not?
5. Compute the orientation of the borehole with respect to magnetic north
without axial field correction.
6.
Write an interactive computer program for solving the above questions.
Solution
1.
i
=
48.2"; 3
mA.
2.
TF
=
+26.5";
turning right.
3.
Drill collar magnetic field
=
0.0178
G;
H7
corrected
=
0.468
G.
4.
h
=
30"
from vertical.
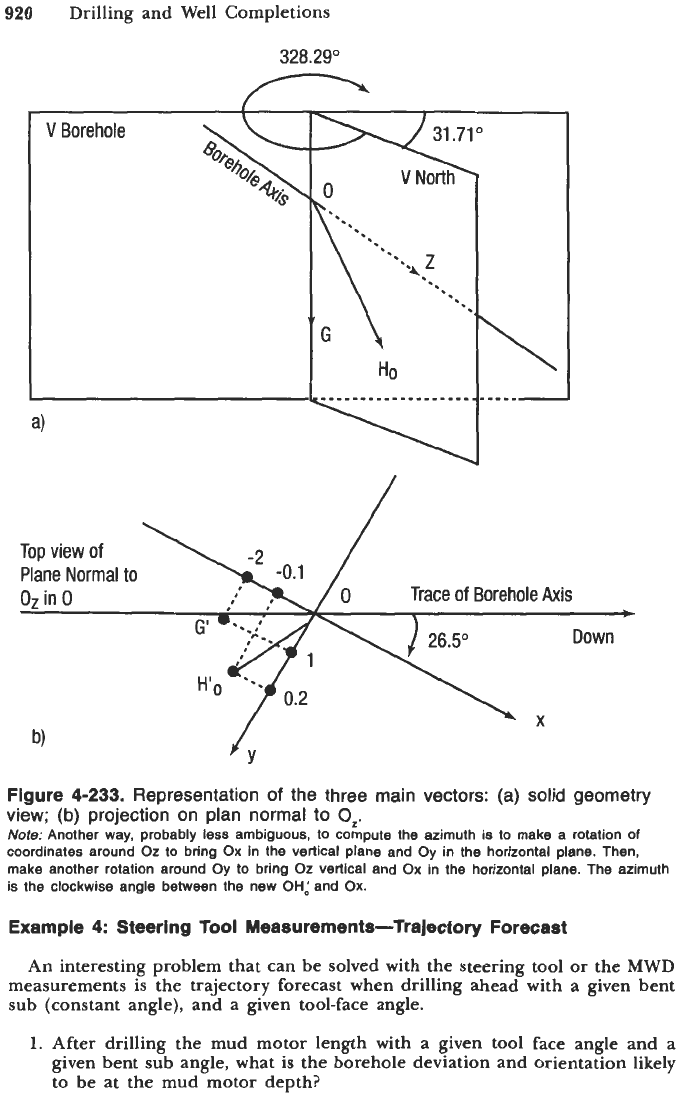
5. One way of making the calculation is to use the three vectors:
G
(Gx,
G
,
GI)
z
(0,
0,
1)
(See Figure
4-233
a and b).
a. Compute the coordinates of vector A normal to vector
G
and vector
H.
Vector
A
=
cross-product of vector
G
by vector
H.
b. Compute the coordinates of vector
B
normal to vector
G
and vector
Z.
Vector
B
=
cross-product of vector
G
by vector
Z.
c. Compute the angle between vector
A
and vector
B.
Being both normal
to vector
G,
they are in the horizontal plane. The angle represents the
azimuth. In some configurations
180"
must be added. The angle is
computed by making the scalar product of vector
A
by vector
B.
H
(Hx,
dy?
HJ
A
B
=
(AI
IBI
cos Az
=
AxBx
+
AyBy
+
AzBz
Care must be exercised since cos(Az)
=
cos(-Az).
d. Numerical results: Angle between vertical planes,
31.71";
azimuth,
328.29".
920
Drilling and Well Completions
328.29'
/
Top
view
of
Plane Normal
to
Oz
in
0
Trace
of
Borehole
Axis
+
Down
X
b)
Oz
in
0
Trace
of
Borehole
Axis
+
Down
X
b)
Figure 4-233.
Representation
of
the three main vectors: (a) solid geometry
view;
(b)
projection on plan normal to
0,.
Note:
Another way, probably less ambiguous, to compute the azimuth is to make a rotation
of
coordinates around
Oz
to bring
Ox
in the vertical plane and Oy
in
the horizontal plane. Then,
make another rotation around Oy to bring
Oz
vertical and
Ox
in the horizontal plane. The azimuth
is the clockwise angle between the new
OH:
and
Ox.
Example 4: Steering
Tool
Measurements-Trajectory Forecast
An interesting problem that can be solved with the steering tool
or
the
MWD
measurements
is
the trajectory forecast when drilling ahead with a given bent
sub (constant angle), and
a
given tool-face angle.
1.
After drilling the mud motor length with a given tool face angle and a
given bent sub angle, what is the borehole deviation and orientation likely
to be at the mud motor depth?
MWD
and
LWD
921
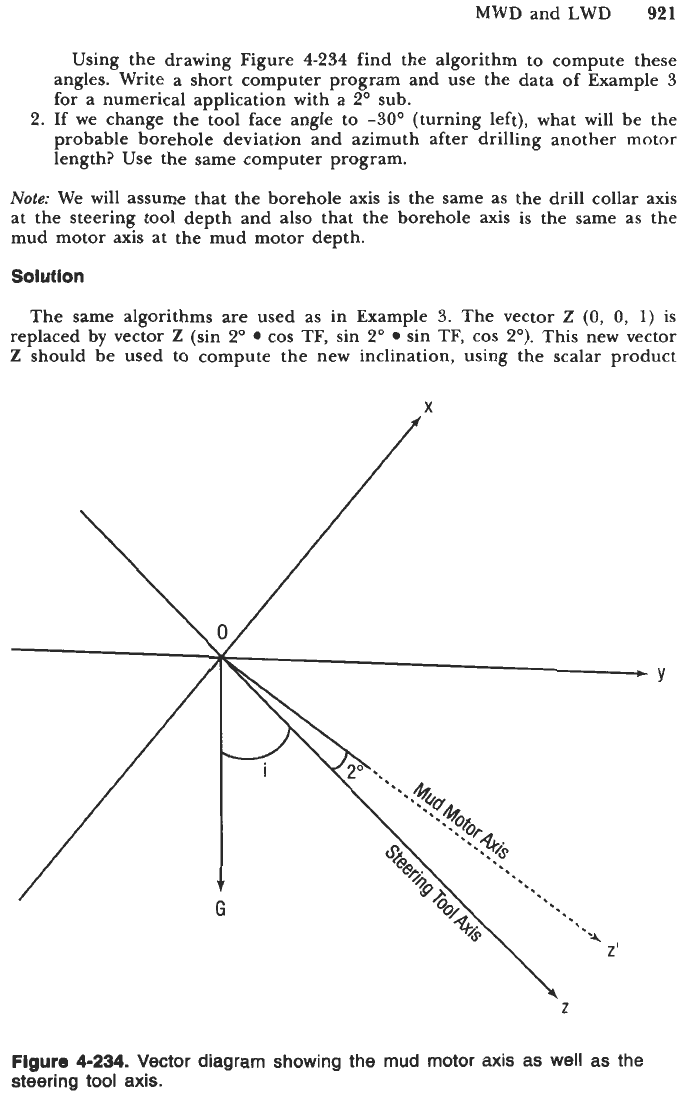
Using the drawing Figure
4-234
find the algorithm to compute these
angles. Write a short computer program and use the data of Example
3
for a numerical application with a
2"
sub.
2.
If we change the tool face angle to
-30"
(turning left), what will be the
probable borehole deviation and azimuth after drilling another motor
length? Use the same computer program.
Note:
We will assume that the borehole axis
is
the same as the drill collar axis
at the steering tool depth and also that the borehole axis is the same as the
mud motor axis at the mud motor depth.
Solution
The same algorithms are used as in Example
3.
The vector
Z
(0, 0,
1)
is
replaced by vector
Z
(sin
2'
cos TF, sin
2"
sin TF, cos
2").
This new vector
Z
should be used to compute the new inclination, using the scalar product
Figure
4-234.
Vector diagram showing the mud motor axis as well as
the
steering tool axis.

922
Drilling and Well Completions
L
3
between vector
G
and new vector
Z.
The new vector
Z
should also be used to
compute the new azimuth.
Vibrations and
Shocks
Measurements while drilling are made with sensors and downhole electronics
that must operate in an environment where vibrations and shocks are sometimes
extremely severe.
A
brief study of vibrations and shocks will be made to
understand better the meaning of the specifications mentioned earlier.
The vibration frequencies encountered during drilling are well known. They
correspond to the rotation of the drill bit, to the passing of the bit rollers over the
same hard spot on the cutting face, and to the impact of the teeth. Figure
4235
gives the order of magnitude for frequencies in hertz
(60
rpm
=
1
Hz). In each
type the lowest frequencies correspond to rotary drilling and the highest ones
correspond to turbodrilling. Three vibrational modes are encountered:
1.
axial vibrations due to the bouncing of the drill bit on the bottom
2. transverse vibrations generally stemming from axial vibrations by buckling
3.
angular vibrations due to the momentary catching of the rollers
or
stabilizers
In vertical rotary drilling, the drillpipes are almost axially and angularly free.
Therefore, the highest level of axial and angular vibration is encountered for
this type of drilling. In deviated rotary drilling, the rubbing of the drill string
on the well wall reduces axial vibrations, but the stabilizers increase angular
vibrations. In drilling with a downhole motor, the rubbing of the bent sub on
the well wall reduces the amplitude of all vibrations.
Vibrations are characterized by their peak-to-peak amplitude at low frequencies
or
by their acceleration at high frequencies. Assuming that vibration is sinusoidal,
the equation for motion is
or mechanical resonance
30
25(
r
I
15
A.
2
x
=
-sin2af
x
t
~~ ~
Rotation
Ro
I
le
rs
Teeth
(4-1
77)
100
1
Frequencies
1
10
.
Hz
Figure
4-235.
Main vibration frequencies encountered while drilling.

MWD
and
LWD
923
Axial
Vibrations
where x
=
elongation in m
f
=
frequency in Hz
t
=
time in
s
A
=
peak-to-peak amplitude in
m
I
30
I
250
I
I
///I/////
2
-
100
MM-CC
By deriving twice, acceleration becomes
A
2
a
=
--(2nf)'sin2nf
x
t
(4-178)
Maximum acceleration is thus am
=
2An2P. For example, peak-to-peak 12 mm at
10
Hz
corresponds to am
=
11.8
m/s2
=
1.2 g. Acceleration of gravity is expressed
as g.
Very few vibration measurements are described in the literature, but the
figures in Figure 4-236 can be proposed for vertical rotary drilling. The lower
limits correspond to soft sandy formations and the upper limits to heterogeneous
formations with hard zones. Table 4-120 gives the specifications that the
manufacturers propose for several tools.
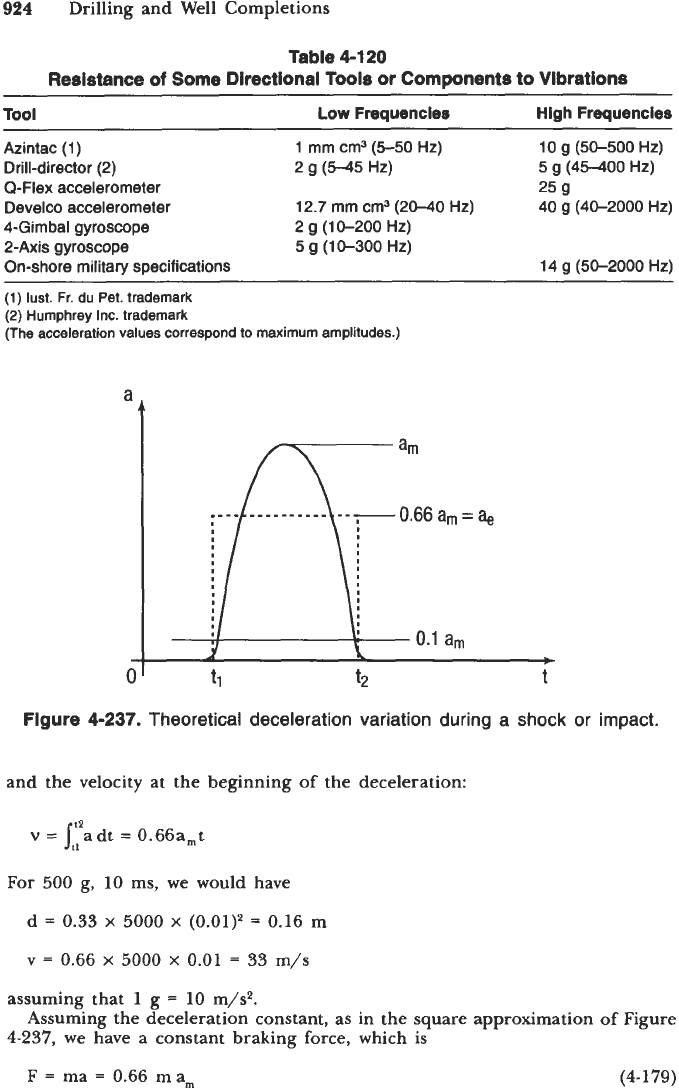
The shocks that measuring devices are subjected to are generally characterized
by an acceleration (or deceleration) and a time span. For example, a device is
said to withstand
500
g
(5,000
m/s') for
10
ms. This refers to a "half-sine." Shock
testing machines produce a deceleration impulse having the form shown in
Figure 4-237.
In the preceding example, a,
=
500
g, t,
-
t,
=
10
ms. The impulse represented
as a solid line is approximately equivalent to the rectangular amplitude impulse
0.66 a,. This impulse can be used for calculating the deceleration distance,
which is
1
2
d
=
Jjt:adt
=
-0.66a,t2
Transverse
Vibrations
1
-
50
MM-CC
I
I
I
I
Angular
Vibrations
Frequencies
1
Hz
10
100
300
Figure
4-236.
Order
of
magnitude
of
the vibration amplitudes encountered
during drilling.
944
Drilling and Well Completions
Table 4-120
Resistance
of
Some Directional Toois
or
Components to Vibrations
Tool
Low
Frequencies
High
Frequencies
~~
Azintac
(1)
Drill-director
(2) 2
g (5-45
Hz)
5
g
(45-400
Hz)
0-Flex accelerometer 25 9
Develco accelerometer
4-Gimbal gyroscope
2-Axis gyroscope
On-shore military specifications
1
mm cm3 (5-50
Hz)
10
g (50-500
Hz)
12.7
mm cm3
(20-40
Hz)
2
g (1 !I-200
Hz)
5 g (1
0-300
Hz)
40 g
(40-2000
Hz)
14 g
(50-2000
Hz)
~~
(1)
lust. Fr. du Pet. trademark
(2)
Humphrey Inc. trademark
(The acceleration values correspond
to
maximum amplitudes.)
a
b
0'
tl
t
Figure 4-237.
Theoretical deceleration variation during a shock or impact.
and the velocity at the beginning
of
the deceleration:
v
=
(::adt
=
0.66amt
For
500
g,
10 ms, we would have
d
=
0.33
x
5000
x (0.01)2
=
0.16
m
v
=
0.66
x
5000
x
0.01
=
33 m/s
assuming that 1 g
=
10 m/s2.
4-237, we have a constant braking
force,
which is
Assuming the deceleration constant, as in the square approximation
of
Figure
F
=
ma
=
0.66 mam
(4-179)
