Лупанов О.Б. Курс лекций по дискретной математике

Подождите немного. Документ загружается.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

имени М. В. ЛОМОНОСОВА

Механико-математический факультет

Курс лекций по

дискретной математике

Лектор — Олег Борисович Лупанов

IV курс, 7 семестр, поток математиков

Москва, 2006 г.

Оглавление

1. Комбинаторика и теория графов 4

1.1. Введение в комбинаторику . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.1. Простейшие комбинаторные объекты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.2. Оценки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2. Теория графов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2.1. Графы. Правильная реализация. Критерий Понтрягина – Куратовского . . . . . . . . . . . 5

1.2.2. Оценки количества деревьев и графов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

1.2.3. Ориентированные графы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.2.4. Двудольные графы. Критерий Холла . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.3. Формальные степенные ряды и производящие функции . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.3.1. Формальные степенные ряды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.3.2. Формальное дифференцирование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

1.3.3. Сходимость в пространстве формальных рядов . . . . . . . . . . . . . . . . . . . . . . . . . 13

1.3.4. Подсчёт количества неприводимых многочленов над F

. . . . . . . . . . . . . . . . . . . . . 14

1.3.5. Формула обращения Мёбиуса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

1.3.6. Тождества Ньютона . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

1.3.7. Что ещё можно делать со степенными рядами? . . . . . . . . . . . . . . . . . . . . . . . . . . 17

1.3.8. Принцип включений и исключений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

2. Кодирование 18

2.1. Общая теория кодиров ания и сжатия информации . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

2.1.1. Схемы кодирования. Коды с однозначным декодированием . . . . . . . . . . . . . . . . . . 18

2.1.2. Неприводимые слова . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

2.1.3. Проверка однозначности декодирования . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

2.1.4. Неравенство Мак-Миллана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

2.1.5. Оптимальные коды. Код Хаффмана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

2.2. Коды с исправлением ошибок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2.1. Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2.2. Коды Хемминга . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2.3. Свойства кодов, исправляющих ошибки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2.4. Коды с исправлением нескольких ошибок . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

2.2.5. Линейные коды . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

2.2.6. Код Хемминга как пример линейного кода . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

2.3. Коды БЧХ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

2.3.1. Эффективное построение корректирующих кодов . . . . . . . . . . . . . . . . . . . . . . . . 25

2.3.2. Построение поля из 2

элементов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

2.3.3. Двоичные коды БЧХ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

2.4. Алгоритм Питерсона . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

2.4.1. Теория . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

2.4.2. Практика . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

3. Схемы из функциональных элементов 27

3.1. Схемы из функциональных элементов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

3.1.1. Метод Шеннона синтеза схем . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

3.1.2. Асимптотически наилучший метод построения схем . . . . . . . . . . . . . . . . . . . . . . . 29

3.1.3. Асимптотическая оценка снизу для сложности схем . . . . . . . . . . . . . . . . . . . . . . . 30

3.2. Инвариантные кла ссы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

4. Теория автоматов 33

4.1. Автоматы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

4.1.1. Детерминированные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

4.1.2. Автоматы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

4.2. Регулярные события. Теорема Клини . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.2.1. Регулярные события . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.2.2. Свойства регулярных множеств . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.2.3. Обобщённые источники. Доказательство теоремы Клини . . . . . . . . . . . . . . . . . . . . 36

4.2.4. О том, чего не могут авто маты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

Предисловие

Порядок изложения материала наиболее соответствует курсу 2005 г.

Огромное спасиб о Сергею Гладких за сотрудничество и набор главы про кодирование. В данной версии

исправлено ещё неско лько опечаток, написан параграф про формулу включений-исключений, а также алгоритм

сжатия по Хаффману.

За поиск лажи в ы носится благодарность Ире Шитовой, Мише Левину, Мише Берштейну и Юре Притыкину.

Последняя компиляция: 26 января 2006 г.

Обновления документа — на сайте http://dmvn.mexmat.net.

Об опечатках и неточностях пишите на dmvn@mccme.ru.

Введение

Курс условно можно разделить на насколько частей:

• Комбинаторный анализ

• Теория графов

• Кодирование

• Теория сложности

• Теория автоматов

• Регулярные языки

1. Комбинаторика и теория графов

1.1. Введение в комбинаторику

1.1.1. Простейшие комбинаторные объекты

Вообще, теория графов — это геометрическая модель комбинаторных объектов.

Будем обозначать через M

множество из n элементов. Без ограничения о бщности можно считать, что

= {1, . . . , n}.

Определение. Пере становкой множества M называется произвольная биекция π : M → M. Очевидно, что

для n-элементных множеств количество всевоз можных перестановок равно n!.

Определение. Назовём размещени ем из n элементов по k любое упорядоченное множество (i

, . . . , i

), где

∈ M

. Количество всевозможных размещений из n элементов по k обозначается A

Утверждение 1.1. Справедливо равенство

= n(n − 1) · . . . · (n − k + 1). (1)

 Первый из k элементов можно в ы брать n способами, второй — (n − 1) способом, и т. д. Пос ледний, k-й

элемент, можно выбрать (n −k + 1) способами. Поэто му число размещений равно указанному произведению. 

Определение. Сочетание — это неупо рядоченное размещение. Говоря более формально, сочетание из n эле-

ментов по k — это произвольное подмножество n-элементного множества. Количество сочетаний из n элементов

по k обоз начается C

или





Утверждение 1.2. Справедливо равенство

(2)

 Рассмотрим произвольное сочетание. Всевозможными перестановками из него можно получить k! раз-

личных размещений, причём для разных сочетаний получаются, естественно, непересекающиеся наборы разме-

щений. Это означает, что количество размещений в k! б ольше числа сочетаний. 

Ясно, что

n(n − 1)(n − 2) · . . . · (n − k + 1)

1 · 2 · . . . · k

n(n − 1 )(n − 2) · . . . · (n − k + 1) · (n − k) · . . . · 1

1 · 2 · . . . · k · (n − k) · . . . · 1

k!(n − k)!

(3)

Из последней формулы очевидно, что C

= C

n−k

. У этой формулы есть и другое обоснование: существует

биекция между k-элементными подмножествами и их (n − k)-элементными дополнениями.

Утверждение 1.3. Справедливо равенство

k=0

= 2

. (4)

 Из формулы бинома Ньютона, применённой к (1 + 1)

, доказываемая фо рмула следует немедленно.

Однако, дадим второе доказательство. Поскольку C

— это количество k-элементных подмножеств, то искомая

сумма — это количество всех подмножеств n-элементного множества. А всех подмножеств в n-элементном мно-

жестве ровно столько, сколько существует последователь ностей из нулей и единиц длины n (если i-й элемент

есть в множестве, то ставим 1, иначе ставим 0). А таких последовательностей, очевидно, 2

. 

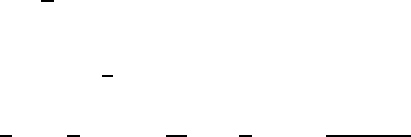
Определение. Сочетание с повторениям и из n элементо в по k — это произвольный наб ор (i

6 i

6 . . . 6 i

), где i

∈ M

. Количество различных таких наборов мы будем обозначать CC

(от англ. complete

combination).

Утверждение 1.4.

= C

n+k−1

= C

n−1

n+k−1

. (5)

 Придумаем хорошую интерпретацию для числа сочетаний с повторениями. Именно, рассмотрим k ша-

риков, расположенных в ряд. Возьмём n − 1 «перегородку» (тогда образуется как раз n ячеек) и воткнём их

между шариками. Тогда количество ша риков до первой перегородки — это в точности количество объектов

первого типа, количество шариков между перво й и второй перегородкой — это количество объектов второго

типа, и так далее. Итак, мы установили биекцию между расположениями перегородок и сочетаниями. А теперь

сопоставим каждой расстановке перегородок набор из нулей и единиц: пусть нулю соответствует перегородка,

а единице — шарик. Тогда всякая расстановка перегородок кодируется строкой из n − 1 + k нулей и единиц, в

которой ровно k единиц. Осталось посчитать такие наборы. Это легко: достаточно расставить, например, еди-

ницы, а нули сами найдут своё место. Очевидно , что количество способов расставить единицы — это C

n+k−1

Второе равенство сразу следует из симметричности биномиальных коэффициентов. 

Замечание. Из определения числа сочетаний с пов торениями ясно, что количество монотонных функций

f : M

→ M

— это в точности количество сочетаний с повторениями CC

1.1.2. Оценки

Получим оценки для числа n! (они нам потребуются в дальнейшем). В качестве очень грубой верхней оценки

можно использовать оценку

n! 6 n

. (6)

Утверждение 1.5. Справедливо неравенство

n! >





. (7)

 Для n 6 8 нерав е нство очевидно, потому что при таких n справа стоит число, не превосходящее 1. Пусть

теперь n > 8. Будем доказывать по индукции. Положим k :=





n! = 1 · 2 · 3 · . . . · k · (k + 1) · . . . · n









n−k









n−k

· 2

n−k

Поясним переход, отмеченный знаком «!». Для оценки первой группы множителей пользуемся предположением

индукции, а вторую группу множителей оцениваем снизу меньшим из сомножителей в соответствующей степени.

Осталось оценить показатель степени: 3k + n 6 3n при n > 8, поэтому всё доказано. 

Что касается чисел сочетаний с повто рениями и без повторений, то для них мы чаще всего будем использовать

такие оценки:

6 2

, CC

6 2

n+k−1

. (8)

Они очевидным образом следуют из определения числа сочетаний.

Надо сказать, что, хотя э то оценки достаточно грубы, на м их вполне будет хватать. Вообще в этом курсе нам

придётся бороться з а константы один-единственный ра з — при доказательстве асимптотики сложности схем из

функциональных элементов.

1.2. Теория графов

1.2.1. Графы. Правильная реализация. Критерий Понтрягина – Куратовского

Определение. Пусть за дано множест во V = {v

, . . . , v

, . . .} и множество E = {e

, . . . , e

, . . .}. Пусть каж-

дому элементу e ∈ E поставлена в соответствие неупорядоченная пара элементов {v, w} множест ва V (при этом

может быть так, что v = w). В этом случае говорят, что задан граф с множеством вершин V и множеством

рёбер E. Вершины v и w, соответствующие ребру e, называют ся концами ребра e. Этот факт удобно записывать,

например, так: Ver(e) = {v, w} (от англ. vertex — вершина).

Определение. Вершина называется изолированной, если в графе нет ребра с концом в этой вершине. Если

два ребра соединяют одну и ту же пару вершин, то гово рят, что это кратные (параллельные) рёбра. Вершина

называет ся концевой, если из неё выходит только одно ребро.

Замечание. Если в определении графа мы потребуем, чтобы пара вершин, соответствующих ребру, была

упорядоченной, мы получим определение ориентированного графа.

Всякий граф можно реализовать в ев клидо вом про странстве. Отметим на плоскости столько различных

точек, сколько вершин в нашем графе, а потом соединим кривыми те вершины, которые соединены рёбрами

(эти кривые тоже будем называть рёбра ми). При этом может получиться так, что некоторые рёбра пересекаются.

Определение. Говорят, что граф допускает правильную реализацию, если можно так расставить вершины

и так провести рёбра, что любые два ребра не будут иметь общих точек (кроме, быть может, с амих вершин).

Утверждение 1.6. Всякий граф, у которого не более континуума вершин и не более континуума рёбер,

допускает прави льную трёхмерную реализацию.

 Рассмотрим произвольную прямую в R

и отметим на ней все вершины графа. Теперь рассмотрим

пучок плоскостей, проходящих через эту прямую. Их там много, поэт ому для каждого ребра можно выбрать

свою плоскость . После этого всё тривиально — соединяем вершины дугой окружности, лежащей в плоскости,

соотв е тствующей данному ребру. Эти дуги не будут пересекаться, потому что разным рёбрам соответ ствуют

разные плоскости. 

Определение. Подграфом графа (V, E) называется такая пара (V

′

, E

′

), что V

′

⊂ V , E

′

⊂ E, и множество

концов рёбер множества E

′

содержится в множестве V

′

Определение. Будем называт ь графы Γ(V

, E

) и Γ(V

, E

) изоморфными, если существуют такие биекции

между их рёбрами и между в е ршинами, что соответствующие рёбра соединяют соответствующие вершины.

Иначе говоря, если ϕ: V

→ V

, а ψ : E

→ E

— биекции, то для всех e ∈ E

должно быть выполнено ϕ(Ver(e)) =

= Ver (ψ(e)).

Введём операцию подразбиения ребра: ставим где-нибудь на ребре (но не в концах) ещё одну вершину, и у

нас получается новый гра ф, у которого вершин на одну больше и рёбер на одно больше (то есть большое ребро

исчезает, остаётся две «половинки»).

Если в г рафе подразбить несколько рёбер, то будем назыв ать новый граф подразбиением исходного.

Определение. Будем говорить, что Γ

и Γ

гомеоморфны, если существуют их подразбиения, изоморфные

между собой.

Определение. Граф K

— это полный граф, построенный на 5 вершинах (рис. 1).

Рис. 1. Граф K

Определение. Граф K

3,3

— это граф, показанный на рис. 2.

Рис. 2. Граф K

3,3

Справедливо следующее утверждение, которое мы доказывать не будем.

Теорема 1.7 (Критерий Понтрягина – Куратовского). Конечный граф допускает планарную правил ь-

ную реализаци ю тогда и т олько т огда, когда не содержит в себе подграфов, гомеоморфных K

3,3

и K

Следующие несколько о пределений интуитивно ясны, мы не будем давать их слишком формально. Все и так

понимают, чего хочется от того или ино г о определения. Они здесь написаны скорее для того, чтобы з нать, что

было на лекции.

Определение. Путь в г рафе Γ(V, E) — это упорядоченный набор рёбер, в котором конец любого предыду-

щего ребра совпадает с началом следующего.

Определение. Цикл — это путь, у которого начало и конец совпадают.

Определение. Граф называется связным, если из любой вершины в любую сущ е ствует путь . По определе-

нию, граф из одной вершины считается св я з ным.

Определение. Дерево — это связный граф без циклов.

Определение. Дерево с корнем — это дерево, у которого помечена одна вершина.

Изоморфизм деревье в с корнями — это изоморфизм графов, при котором корень переходит в корень. Пусть

δ(q) — количество неизоморфных деревьев с q рёбрами, а δ

∗

(q) — количество неизоморфных деревьев с корнями

с q рёбрами. Очевидно, что δ(q) 6 δ

∗

(q).

Утверждение 1.8. В любом конечном связном графе существует подграф, содержащий все вершины ис-

ходного графа и являющийся деревом.

 Будем разрезать циклы, пока их не останется. При разреза нии цикла с вязность не нарушается. Посколь-

ку рёбер конечное число, процесс когда-нибудь ос тановится. 

Следствие 1.1. Всякий связный граф можно получить из дерева достройкой рё бер.

Утверждение 1.9. Если в дереве p вершин, то в нём p − 1 ребро.

 Докажем индукцией по числу вершин. Найдём концевую вершину и удалим её. При этом пропадёт ровно

одна вершина и ровно одно ребро. Оставшийся граф тоже будет деревом с меньшим количеством вершин. 

1.2.2. Оценки количества деревьев и графов

Напомним обозначение M

= {1, . . . , q}.

Теорема 1.10. Имеет место оценка

∗

(q) 6 4

. (9)

 Возьмём дерево и расположим его листья ст рого по ярусам, чтобы корень был в самом низу. Далее

пронумеруем ве рш ины номерами от 0 до q, идя слева направо, сверху вниз, то есть заметая ярус за ярусом

слева направо. Ясно, что при такой нумерации корень получит номер q. Теперь поставим в соответ с твие каждому

такому пронумерованному дереву некоторую моното нную функцию. Возьмём любую вершину (кроме корня) с

номером k. Спустимся по ней на один шаг к корню. Мы попадём в вершину, в которой будет написано какое-то

число m. Тогда пусть наша функция в точке k + 1 принимает значение m. Это б удет функция, у которой

область определения — множе с тво M

, а обла сть значений содержится в множестве M

. Легко про верить, что

если нам дана какая-нибудь монотонная функция , то по ней можно либо однозначно вырастить дерево, которое

ей соо тветствует (точнее говоря, если вообще можно, то уж единственным образом). Действительно, возьмём

полный прообра з точки q. Его мощность — это в точности количество рёбер, которые растут от корня. Нарисуем

их. Далее, возьмём самую правую вершину, она получит номер q −1. Снова берем прообраз, и так далее (если

прообраз пуст, то это значит, что данная вершина является концевой). Затем переходим к следующей вершине

в том же яруса, двигаясь справа налево. В итоге мы раскодируем всё дерево.

Итак, мы устроили инъективное отображение из множества деревьев с корнями в множе ство монотонных

функций f : M

→ M

. А их количество мы зна е м — это CC

= C

2q−1

6 2

2q−1

6 4

. Стало быть, различных

деревьев с корнем и того меньше. 

Утверждение 1.11. Количество δ(q) неизоморфных деревьев с q рёбрами оценивается снизу:

δ(q) >

√



√



. (10)

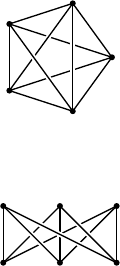
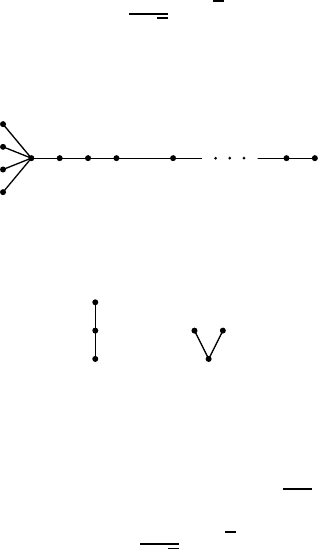
 Возьмём цепочку из t рёбер, в ней будет t + 1 в ершина. Расположим эту цепочку горизонтально, и к

самой левой вершине прицепим 4 ребра, чтоб ы сделать её особой (см. рис. 3).

0 1 2

Рис. 3. Дерево

К остальным вершинам будем цеплять деревья из двух рёбер, изображённые на рис. 4 (первое будем коди-

ровать нулём, вто рое — единицей).

Рис. 4. Поддеревья

К каждой из t вершин можно прицепить любое из этих двух деревьев, поэтому количество таких деревьев

получается равным 2

. Они, очевидно, неизоморфны между собой. Посчитаем количество рёбе р у такой кон-

струкции. Скелет дерева состоит из t рёбер, к каждой из t в е ршин добавляется по 2 ребра, и ещё 4 ребра

добавлено к особой вершине. Таким образом, q = 3t + 4. Отсюда t =

q−4

, поэтому

δ(q) > 2

√



√



, (11)

что и требовалось доказать. 

Замечание. На самом деле можно доказать (Otter, 1948), что основание степени не меньше, чем 2.98.

Доказательство Оттера существенно использует ТФКП.

Утверждение 1.12. Количество γ(q) неизоморфных связных графов с q рёбрами. оценивается сверху:

γ(q) 6 (Cq)

, C = const . (12)

 У каждого ребра два конца. Можно считать, что количество вершин рав но 2q, потому что во всякий

граф можно доб авить нужное количество изолированных вершин (полу ченные графы тоже будут неизоморфны,

потому что у каждого из них найдётся по связной компоненте, не изоморфной никакой связной компоненте

другого графа). Занумеруем вершины, тогда каждое ребро — это пара чисел. Посчитаем количество различных

сортов рёбер. С учётом петель, их ровно CC

= C

2q+1

= q(2q + 1) =: s шту к. Теперь у нас ест ь s сортов рёбер,

и из них нужно (возможно, с повторениями, потому что графы могут иметь кра тные ребра) выбрать q штук.

Значит,

γ(q) 6 CC

= C

s+q−1

(s + q − 1)





. (13)

Имеем s + q − 1 6 2q

+ q + q 6 4q

. Отсюда получаем оценку

γ(q) 6

(4q

)





= (32q)

, (14)

то есть в качестве константы C можно взять C = 32. 

Через γ(p, q) будем обозначать количество связных графов с p вершинами и q рёбрами.

Утверждение 1.13. Для количества графов справедлива оценка сверху:

γ(p, q) 6 p

q−p

· A

q+p

, A = const . (15)

 Расс мотрим про извольное p-вершинное дерево. Чтобы из p-вершинного дерева сделать q-рёберный граф,

нужно дополнительно провести ещё q−(p−1) = q−p+1 =: k ребро. Из каждой вершины дерева можно выпустить

куда-то ребро (так, чтобы вто рой конец болтался в воздухе). Это можно сделать, очевидно, CC

способа ми.

Теперь эти концы надо как-то подсоединить к имеющимся вершинам. Это можно сделать p

способа ми. З начит,

существует не более CC

·p

способо в получить из дерева граф. А поскольку количество деревьев не превосходит

p−1

, то в итоге имеем оценку

γ(p, q) 6 4

p−1

· CC

· p

= 4

p−1

· C

p+k−1

· p

= 4

p−1

· C

· p

6 4

p−1

· 2

· p

q−p

· p

6 8

· 8

· p

q−p

. (16)

В последней оценке, отмеченной «!», мы о чень сильно всё загрубили: 4

p−1

6 4

, p 6 2

и, наконец, 2

6 8

Таким образом, достаточно взять A = 8. 

До сих пор мы рассматривали только связные графы. Теперь получим оценки для графов с заданным

количеством компонент связности r. Ко личество таких графов мы будем обозначать символом γ(p, q, r).

Утверждение 1.14. Имеет место нераве нство

γ(p, q, r) 6 p

q−p

· B

q+p+r

. (17)

 Граф Γ(p, q, r) состоит из r связных графов Γ(p

, q

), . . . , Γ(p

, q

), причём p =

, q =

. Ясно, что

при фиксированных наборах {p

} и {q

} количество оценивается произведением

i=1

γ(p

, q

) 6 A

· p

−p

· . . . · A

· p

−p

6 A

q+p

· p

q−p

. (18)

Итак, оценено каждое слагаемое. Теперь нам нужно оценить количество таких слагаемых, то есть посчитать

количество возможных наборов {p

} и {q

}. Разбиения набора p не допуска ют нулевых слагаемых (потому что в

каждом графе должна быть хотя бы одна вершина), а разбиения числа q допускают нулев ы е слагаемые (рёбер

может не б ыть вовсе). Посмотрим, что значит разбить число p на r слагаемых, среди которых не может быть

нулевых. Напишем подряд p единиц и будем между ними расставлять r − 1 знак «+», то есть для расстановки

есть p−1 позиция, при этом два знака не могут стоять рядом. Значит, в перв ом случае имеем дело с сочетаниями

без повторений, а их C

r−1

p−1

6 2

p−1

Во втором случае надо разбить число q на r слагаемых, среди которых могут быть нулевые. Будем тоже

расставлять знаки «+» среди q, но теперь их можно ставить в самом начале и в с амом конце, то есть позиций

q + 1 штука, и кроме того, можно два плюса ставить подряд, то есть эт о сочетания с повторениями. Поэтому

их количество равно CC

r−1

q+1

= C

r−1

q+r−1

6 2

q+r−1

. Значит, количество разбиений заведомо не превосходит 2

p−1

q+r−1

6 2

p+q+r

. Таким образом,

γ(p, q, r) 6 A

q+p

· p

q−p

· 2

p+q+r

6 A

p+q+r

· p

q−p

, (19)

поскольку A > 2. Таким образом, в качестве константы B можно взять A, но это не так важно. 

1.2.3. Ориентированные графы

Определение. Назовём граф ориен тированным, если каждому его ребру приписано направление.

Определение. Ориентированн ый цикл — цикл, в котором все рёбра направлены в одну ст орону, т. е. ко-

нечная последовательность ориентированных рёбер



−−−−→

, v

i+1



, где первая вершина совпадает с последней.

Лемма 1.15. В любом конечном ориен т ированном графе без ориентированных циклов есть вершина, из

которой рёбра не выходят.

 От противного: выберем любую вершину и, выходя из неё, будем двигаться по рёбрам в направлении,

приписанном данному ребру. Если из каждой вершины выходит хотя бы одно ребро, то рано или поздно мы

вернёмся туда, где уже были, поскольку граф конечен. Но эт о будет ориентированный цикл. Противоречие. 

Теорема 1.16. В любом конечном ориентированном графе без ориент ированных циклов можно зануме-

ровать вершины первым и натуральными числами так, что каждое ребро будет направлено от вершины с

меньшим номером в вершину с большим номером.

 Докажем индукцией по числу вершин p. При p = 1 утверждение очевидно. Пусть p > 1. П редположим,

что это верно для всех графов с числом вершин, меньшим p. Рассмотрим граф с p вершинами. По лемме у него

есть вершина, из которой рёбра не выходят. Уберём из графа эту вершину и все входящие в неё рёбра, получим

граф с числом вершин, меньшим p. По предположению индукции такой граф допускает искомую нумерацию

вершин числами 1, 2, . . . , p − 1 . Тогда присвоим выкинутой в ершине номер p. 

1.2.4. Двудольные графы. Критерий Холла

Определение. Пусть множество ве ршин графа разбито на два подмножества U и L. Граф называется

двудольным, если концы любого ребра лежат в разных подмножествах.

Пример 2.1. Примеры двудольных г рафов (рис. 5):

[NO PICTURE AVAILABLE YET]

Рис. 5. Двудольные и не двудольные графы

Условимся называть подмножество U верхним, а L — нижним. Будем рисо вать двудольные графы в соот-

ветствии с этими названиями.

Определение. Говорят, что задано паросочетание в двудольном графе, если для каждой верхней вер-

шины зафиксировано по одному ребру (идущему в нижнее множество). Фактически это означает, что задано

отображение f : U → E. Па росочетание называется совершенным, если концы выпущенных рёбер при этом не

склеиваются.

Пусть A ⊂ U. Через R(A) будем обоз начать образ бинарного отношения «соединён ребром» в L.

Теорема 1.17 (Критерий Холла). Конечный двудольный граф обладает совершенным паросочетан ием

тогда и только тогда, когда для любого (непустого) A ⊂ U имеем |R(A)| > |A|.

 Необходимость этого условия очевидна: если со вершенное паросочетание нашло с ь, то ясно, что образ

любого подмножества содержит не мень ше вершин, чем само это подмножество (иначе какие-то два ребра,

выходящие из множества A, упёрлись бы в одну вершину в образе).

Докажем достаточно сть. Будем доказывать индукцией по числу n = |U|. База n = 1 очевидна: любое ребро

годится. Пусть всё доказано для n, докажем для n + 1. Возможны два случая.

◦

Для любого непустого A ⊂ U имеем |R(A)| > |A|, то есть по крайней мере |R(A)| > |A| + 1 . Рассмотрим

a ∈ U. По крайней мере одно ребро из неё выходит, пусть оно приходит в вершину b ∈ L. Уберем вершины a и b

из нашего графа вместе со всеми рёбрами, которые в них входят. Получим двудольный граф

Γ с множеств ами

верхних и нижних вершин

U и

L. Покажем, что



. Действительно, рассмот рим множество оставшихся

«претендентов» на вершину b. Для любого подмножества с их участием, но без участия вершины a, неравенств о

было строгим. Образ этого подмножеств а, конечно, захватывает вершину b, но когда мы её уберём, неравенство

лишь превра тится в нестрогое, ибо мы т е ряем всего одну вершину. Все остальные подмножества и вовсе сохранят

строгие равенства. Итак, к новому графу уже применимо предположение индукции, потому что в

U меньше

вершин, чем в U.

◦

Пусть нашлось собственное непустое подмножество A

⊂ U, для которого |R(A

)| = |A

|. Поскольку

оно собств е нное, то в нём уже по предположению индукции существует совершенное паросочетание. Теперь

рассмотрим то, что останется от г рафа, если вырезать A

и R(A

). Если для какого-то множества

A в новом

графе неравенство нарушится, то оно нарушится и для A

∪

A в исходном графе. Значит, можно применить

предположение индукции по-отдельности к множеству A

и к его «дополнению». 

1.3. Формальные степенные ряды и производящие функции

Производящие функции — это замечательный инструмент для того, чтобы что-нибудь посчитать. Чтобы

иметь возможность что-либо про них гово рить, нам нужны формальные степенные ряды.

1.3.1. Формальные степенные ряды

Пусть K — кольцо с 1. Рассмотрим последовате льность {a

} ⊂ K. Построим формальное выражение

∞

i=0

Его мы будем называть форма льным степенным рядом над кольцом K.

Множество формальных степенных рядов над кольцом K будем обозначать K



[x]



. Введём на этом множе-

стве структуру кольца. Определим сложение степенных рядов естественным образом, а именно, если

(A + B)(x) =

∞

i=0

+ b

, где A(x) =

∞

i=0

, B(x) =

∞

i=0

. (20)

Произведение определим так: будем говорить, что C(x) = A(x) ·B(x), если коэффициенты ряда C(x) определя-

ются по формуле c

i=0

k−i

. Два ряда будем называть равными, если у них равны вс е коэффициенты при

соотв е тствующих степенях. Итак, мы получили кольцо формальных степенных рядов с единицей.

Заметим, что подстановка вместо переменной x какого-либо значения вообще лишена смысла. Однако удобно

считать, что подстановка нуля даёт коэффициент a

, поэтому будем по определению с читать, что A(0) = a

для

степенного ряда

∞

i=0

Отметим простые свойства полученного кольца.

• Если кольцо K было ассоциативным (коммутативным), то кольцо K



[x]



тоже будет ассоциа тивным (ком-

мутативным).

• Если в K нет делителей нуля, то их нет и в K



[x]



Замечание. Эти свойства, очевидно, выполнены и в обратную сторону, поскольку K является подкольцом

в K



[x]



Далее мы будем считать, что K — ассоциативное коммутативное кольцо с 1 и без делителей нуля, то есть

область целостности. Выясним, какие элементы в кольце K



[x]



обратимы.

Определение. Если A(x) · B(x) = 1, то говорят, что B = A

−1

Утверждение 1.18. Ряд A(x) обратим тогда и только тогда, когда A(0) обратим в кольце K.

 Попробуем найти коэффициенты ряда B(x) := A

−1

(x) в явном виде. Для этого приравняем коэффици-

енты:

= 1,

+ a

= 0,

. . .

+ . . . + a

= 0,

(21)

Ясно, что эта система разрешима тогда и только то гда, когда a

обратим в кольце K — в этом случае все

коэффициент ы последовательно выражаются через предыдущие:

= −a

−1

k−1

+ . . . + a

), (22)

что и требовалось доказать. 

Следствие 1.2. Если K — поле, то обратимые элементы — это ряды с ненулевым свободным членом.

Пример 3.1.

(1 + x + x

+ x

+ . . .) =

1 − x

. (23)

Заметим, что это чисто алгебраический результат. Никаких геометрических прогрессий мы здесь не суммируем.