Лупанов О.Б. Курс лекций по дискретной математике

Подождите немного. Документ загружается.

Определение. Пусть дана последовательность {a

}. Про изводящей функцией этой последовательности на-

зывается формаль ный ряд

∞

i=0

. (24)

Биномиальные коэффициенты. Пусть x

, . . . , x

— формальные объ екты. Пусть X = {x

, . . . , x

}. Рас-

смотрим всевозможные k-элементные подмножества в множестве X. Это всевозможные выборки x

, . . . , x

Выпишем соответствующую производящую функцию:

(1 + x

) · (1 + x

) · . . . · (1 + x

) =

k=0

S⊂X

|S|=k

∈S

. (25)

Что такое произвольное подмножество в X? Всякий элемент x

либо входит в него (этому соответствует сла гае-

мое x

в соответствующем множителе), либо не входит (это му соответствует слагаемое 1). А теперь, поскольку

нас интересует т олько количество k-элементных подмножеств, можно подставить x

= x и получить искомую

производящую функцию:

(1 + x)

k=0

. (26)

Сочетания с повторениями. В этом случае каждый элемент может вс тречаться уже не один раз, а сколько

угодно. Значит, каждая скобка должна содержать формальную с умму всех степеней переменной x

(1 + x

+ x

+ . . .) · (1 + x

+ x

+ . . .) · . . . · (1 + x

+ x

+ . . .) =

∞

k=0

+...+s

· . . . · x

(27)

После подстановки x

= x получаем производящую функцию:

(1 + x + x

+ x

+ . . . )

∞

k=0

. (28)

Теперь заметим, что у нас слева стоит произведение формальных рядов. А их мы уже умеем сворачивать.

Получаем

(1 − x)

−n

∞

k=0

. (29)

Теперь получим формулу бинома Ньютона для отрицательных степеней:

(1 − αx)

−n

∞

k=0

. (30)

Отметим одно полезное свойство числа сочетаний:

= C

n−1

n+k−1

(k + n − 1) · . . . · (k + 1)

(n − 1)!

, (31)

то есть это многочлен по переменной k степени n − 1.

Теперь рас смотрим ещё один содержат е льный пример, в котором используются производящие функции.

Рассмотрим сначала такую простенькую задачу. Найти число u

последовательностей длины n, в которых нет

двух нулей, стоящих подряд. Идея решения состоит в том, чтобы выразить u

через числа u

с меньшими

номерами (написать рекуррентное соотношение). Попробуем сделать это: ясно, что u

= 1 и u

= 2. Далее, если

у нас есть последовательность w длины n, то возможны два случая:

w = 1 ∗. . . ∗

|{z}

n−1

, w = 01 ∗. . . ∗

|{z}

n−2

. (32)

На месте звёздочек могут стоять любые допустимые пос ледовательности длин n − 1 и n − 2 соответс твенно.

Таким образом, u

= u

n−1

+ u

n−2

. Мы получили линейное рекуррентное соот ношение. Давайте выясним, какой

общий вид могут иметь решения линейных рекуррентных соотношений.

Теорема 1.19. Пусть K = C. Пусть u

, u

, . . . — искомая последовательность. Пусть задано рекур-

рентное соотношение

n+r

= a

n+r−1

+ . . . + a

, a

6= 0 (33)

и заданы начальные условия u

, . . . , u

r−1

. Тогда общий член последовательности u

выражается в виде мно-

гочлена степени строго меньше r:

i=1

(n)α

. (34)

 Расс мотрим производящую функцию этой последовательности:

U(x) =

∞

n=0

. (35)

Рассмотрим многочлен

G(x) := 1 − a

x − a

− . . . − a

. (36)

А теперь перемножим их:

C(x) := G(x) · U (x) =

∞

n=0

. (37)

Заметим, что

n+r

= u

n+r

− a

n+r−1

− . . . − a

(38)

при всех n > 0. Но в силу имеющегося рекуррентного соотно шения получаем, что все коэффициенты ряда,

начиная с r-го, равны нулю. Значит, C(x) — это просто многочлен степени не выше r − 1.

Рассмотрим многочлен

F (x) = x

− a

r−1

− . . . − a

= (x − α

)

· . . . · (x − α

)

= r. (39)

Легко видеть, что

G(x) = (1 − α

· . . . · (1 − α

. (40)

В самом деле, из определения G ясно, что G(x) = x





, но выписанное произведение (40) тоже , очевидно,

равно x





Далее, поскольку

U(x) =

C(x)

G(x)

r−1

i=0

(1 − α

−q

· . . . · (1 − α

−q

. (41)

А теперь применяем формулу для бинома с отрицательными степенями:

min(n,r−1)

i=0



,...,m

>0,

+...+m

=n−i

j=1



. (42)

С другой с тороны, вспомним теорему из анализа о ра з ложении рациональных дробей в сумму простейших:

deg C < deg G, поэтому

U(x) =

C(x)

G(x)

C(x)

(1 − α

· . . . · (1 − α

i=1

k=1

(1 − α

. (43)

Разлагаем в ряды наши «прогрессии» и приравниваем коэффициенты:

U(x) =

i=1

k=1

∞

n=0

i=1

∞

n=0

(n)α

. (44)

Здесь deg P

6 q

− 1 6 r − 1. Окончательно получаем

i=1

(n)α

, (45)

что и требовалось доказать. 

1.3.2. Формальное дифференцирование

Чтобы не напрягать себя лишними проблемами, будем далее считать кольцо K ассоциативным коммутатив-

ным кольцом, потому что ничего другого нам, по сути, и не потребуется.

Определение. Пусть дан формальный ряд A(x). Его формальной производной назовём ряд

DA(x) :=

∞

n=0

(n + 1)a

n+1

. (46)

Очевидно, что производная — это линейная операция.

Несложно проверить, что имеет место формула Лейбница

D(A · B) = DA · B + A · D B. (47)

Кроме того, если ряды A и B обратимы, то имеет место формула (правило ло гарифмического дифференци-

рования)

D(A · B)

A · B

. (48)

Этот результат немедленно следует из формулы Лейбница.

Далее, эта формула без труда обобщается на произво льное количество слагаемых:

D(A

· . . . · A

)

· . . . · A

+ . . . +

. (49)

Из формулы Лейбница легко выводится ещё одно полезное св ойство:

D(A

) = nA

n−1

DA. (50)

1.3.3. Сходимость в пространстве формальных рядов

Верхние индексы будут обозначать не степень, а номер.

Определение. Рассмотрим последовате льность рядов





⊂ K



[x]



. Будем гов орить, что A

→ A, если

для всякого n найдётся δ(n) такое что при всех i > δ(n) имеем a

= a

. Иначе говоря, начиная с некоторого

номера, n-й коэффициент предела стабилизируется.

Определение. Будем гово рить, что формальный ряд, составленный из рядов, сходится, если сходится по-

следовате льность его частичных сумм.

Пример 3.2. Рассмотрим ряды A

(x) := a

. Тогда

(x) = A(x) =

∞

i=0

Определение. Через deg

∗

A будем обозначать номер минимального ненулевого коэффициента ряда A.

Утверждение 1.20 (Критерий сходимости). Ряд

∞

j=0

(x) сходится т огда и только тогда, когда

deg

∗

→ ∞, j → ∞. (51)

 Очевидно. 

Определение. Пусть ряды B

таковы, что B

(0) = 0. Будем говорить, что B(x) =

∞

j=1



1 + B

(x)



, если

последовательность частных произведений

j=1



1 + B

(x)



(52)

сходится к ряду B.

Утверждение 1.21. Бесконечное произведение

∞

j=1



1 + B

(x)



(53)

сходится тогда и только тогда, когда deg

∗

→ ∞ при j → ∞.

 Очевидно. 

Эти свойства сходимости позволяют беспрепятственно перенести операцию дифференцирования на ряды и

произведения. Так, для сходящихся рядов имеет место свойство:

∞

j=1

∞

j=1

, (54)

а для сходящихся про изведений — формула

∞

j=1



1 + B

(x)



∞

j=1



1 + B

(x)



∞

j=1



1 + B

(x)



1 + B

(x)

. (55)

1.3.4. Подсчёт количества неприводимых многочленов над F

Рассмотрим поле F

и кольцо многочленов F

[x].

Определение. Многочлен называется приведённым, если его старший коэффициент равен 1.

Заметим, что произведение приведённых многочленов является приведённым многочленом. Мы будем здесь

рассматривать только приведённые многочлены, поэтому слово «приведённый» часто будем опускать.

Через R

будем обозначать множество всех приведённых многочленов степени k. Заметим, что c

:= |R

| =

, потому что старший коэффициент равен 1, а все остальные k коэффициентов произвольны. Рассмотрим

производящую функцию для последовательности {c

(x) :=

∞

k=0

∞

k=0

1 − px

. (56)

Через I

будем обозначать количество неприводимых многочленов степени m. Вычислим нашу производя-

щую функцию другим способ ом. Покажем, что

(x) =

∞

m=1

(1 + x

+ x

+ . . . )

. (57)

Почему так? Всякий многочлен P как-то разлагается в произведение неприводимых, взяты х в некоторых сте-

пенях. У нас есть большой выбор неприводимых многочленов: I

видов веса 1, I

видов веса 2 и так далее.

Вес многочлена — это прос то е г о степень, то есть тот вклад, который он вносит в степень многочлена P . Что

касается видов, то многочленов каждого вида у нас неограниченное количество (потому что, вообще го воря,

степени сомножителей ничем не ограничены, и потому в каждой скобке бесконечное количество слагаемых).

Множитель m-го веса k-го вида, взятый в с тепени s, соо тветствует одночлену x

из скобки с номером k в m-м

множителе бесконечного произведения.

А теперь начинаем подсчёт. Сворачивая прогрессии и переходя к об ратным рядам, получаем

1 − px =

∞

m=1

(1 − x

)

. (58)

Продифференцируем это тождество, применяя формулу (55):

−p

1 − px

∞

m=1

−x

m−1

1 − x

. (59)

Умножим раве нство на x:

−px

1 − px

∞

m=1

−x

1 − x

. (60)

Выделяя целую часть в дробях, получаем

1 −

1 − px

∞

m=1



1 −

1 − x



. (61)

Раскатывая слагаемые в левой и право й части в прогрессии, полу чаем

∞

k=1

∞

m=1



+ x

+ . . .



. (62)

Приравнивая коэффициенты при подобных членах, получаем

m|k

. (63)

Выведем сначала несколько простых следствий.

◦

Без всяких формул ясно, что I

> 0.

◦

Ясно, что I

= p (это многочлены вида x + a, a = 0, . . . , p − 1).

◦

Из 2

◦

и (63) сразу следует, что при k > 2 имеем I

−p

◦

Заметим, что если k — простое число, то слагаемых в сумме всего два, поэтому I

−p

◦

Получим оценку снизу для чисел I

= kI

m|k

m<k

< kI

k/2

m=0

< kI

+ p

k/2

+ 1. (64)

Здесь переход «!» следует из оценки, полученной в 3

◦

. Стало быть,

− p

k/2+1

. (65)

◦

Из неравенства, полученного в 5

◦

, следует, что I

> 0, т о есть су ществуют неприводимые многочлены

любой степени.

Замечание. В курсе алгебры обычно доказывается, что над конечными полями существу ют неприводимые

многочлены с коль угодно высокой степени. Мы получили некото рое усиление э того утв е рждения, правда, не

для всех конечных полей, а только для полей F

Мы ещё получим явную формулу для вычисления I

, но для этого нам потребуется одна формула , очень

полезная в борьбе с производящими функциями.

1.3.5. Формула обращения Мёбиуса

Пусть f, g : N → R.

Определение. Пусть n = p

· . . . · p

— разложение числа n на простые множители. Функция

µ(n) :=











1, n = 1,

(−1)

, m

= ··· = m

= 1,

0 иначе.

(66)

называет ся функцией Мебиуса.

Лемма 1.22.

d|n

µ(d) =

(

1, n = 1,

0 иначе.

(67)

 При n = 1 доказывать нечего. Пусть теперь n = p

· . . . · p

, а bn = p

· . . . · p

. Тогда

d|n

µ(d) =

d|bn

µ(d) +

d|n

d∤bn

µ(d). (68)

Вторая сумма равна нулю, потому что если d|n и d ∤ bn, то у d есть делители в степенях, больших 1. А первая

сумма соответствует неповторяющимся простым делителям. Количество слагаемых для s делителей, очевидно,

равно C

. Значит,

d|bn

µ(d) = 1 − C

+ C

− C

+ ··· = (1 − 1)

= 0. (69)

Итак, обе суммы в этом случае равны нулю, и лемма доказана. 

Теорема 1.23 (Формула обращения Мёбиуса). Если для всех n выполнено равенство

f(n) =

d|n

g(d), (70)

то

g(n) =

d|n

µ(d)f





. (71)

 Для всякого делителя d числа n имеем





d). (72)

Отсюда

d|n

µ(d)f





d|n

µ(d)

d) =

d : d

d|n

µ(d)g(

d) =

d|n

µ(d)g(

d) =

d|n

µ(d) = g(n), (73)

потому что в силу леммы выживет только то слагаемое, для которого

= 1, то есть когда n =

d. 

Следствие 1.3 (Формула для количества приведённых неприводимых многочле нов).

m|k

µ(m)p

k/m

. (74)

 В предыдущем разделе мы уста новили формулу

m|k

. (75)

Применим формулу обра щения к функциям f (k) = p

и g(k) = kI

. Получим

m|k

µ(m)p

k/m

, (76)

и осталось только разделить это равенство на k. 

1.3.6. Тождества Ньютона

Сейчас мы применим технику работы со степенными рядами над кольцом K[α

, . . . , α

], где K — поле. Этот

страшный объект обозначается, ясное дело, K[α

, . . . , α

]



[x]



Напомним, чт о многочлен f ∈ K[α

, . . . , α

] называется с имметрическим, если он инвариантен относительно

любых перестановок его переменных.

Определим степенные суммы: S

:= α

+ . . .+ α

. Напомним, что элементарные симметрические многочлены

от n переменных имеют вид

= −(α

+ . . . + α

= α

+ α

+ . . . ,

. . .

= (−1)

,...,i

· . . . · α

. . .

= (−1)

· . . . · α

(77)

Рассмотрим

S(x) =

∞

k=1

. (78)

Рассмотрим многочлен

σ(x) = (1 − α

x)(1 − α

x) · . . . · (1 − α

x) = 1 +

k=1

. (79)

Применим формулу логарифмического дифференцирования:

Dσ(x)

σ(x)

k=1

D(1 − α

1 − α

k=1

−α

1 − α

. (80)

Домножая на x это равенст во, получаем

xDσ(x)

σ(x)

k=1



1 −

1 − α



. (81)

Мы знаем, что

1 − α

= 1 + α

x + α

+ α

+ . . . , (82)

поэтому

1 −

1 − α

= − (α

x + α

+ α

+ . . . ), (83)

откуда

k=1



1 −

1 − α



= −



(α

+ . . . + α

)x + (α

+ . . . + α

+ . . .



= −S(x). (84)

Комбинируя эту формулу с фо рмуло й (81), получаем, что

S(x)σ(x) + xDσ(x) = 0. (85)

Но продифференцировать многочлен σ(x) очень легко:

xDσ(x) =

k=1

kσ

, (86)

и окончательно получаем тождество

S(x)σ(x) =

k=1

kσ

. (87)

Приравнивая коэффициенты при степенях x, получаем формулы

0 = S

+ σ

0 = S

+ S

+ 2σ

0 = S

+ S

+ 3σ

. . .

0 = S

+ S

n−1

+ S

n−2

+ . . . + S

n−1

+ nσ

. . .

0 = S

n+i

+ S

n+i−1

+ . . . + S

(88)

Эти соотношения называются формулами Ньютона.

Следствие 1.4. В случае, если char K = 0, многочлены σ

выражаются через степенные суммы.

Следствие 1.5. Всякий симметрический многочлен однозначно выражается через степенные суммы.

1.3.7. Что ещё можно делать со степенными рядами?

Так вот, степенные ряды так и тянет подставить один в другой. Разберёмся, когда это можно делать.

Пусть у нас есть ряд A(x), и мы хотим подставить в нег о ряд B(x). Ясно, что если B(0) 6= 0, то вс ё плохо:

нулевой коэффициент результирующего ряда является бесконечной суммой, чт о не есть хорошо. Поймём те перь,

почему в случае, когда B(0) = 0, всё будет хорошо.

Действительно, если B(0) = 0, то deg

∗

B(x)

> n → ∞ при n → ∞, поэтому со сходимостью ряда



B(x)



∞

n=0

B(x)

(89)

проблем не будет.

Пример 3.3. В качестве примера рассмотрим последова тельность Фибоначчи. . .

1.3.8. Принцип включений и исключений

Пусть имеются объекты x

, . . . , x

и свойства p

, . . . , p

. Через E(m) будем обозначать число объектов,

обладающих ровно m свойствами, а через w(p

, . . . , p

) — число объе ктов, об ладающих свойств ами p

, . . . , p

Положим

W (k) :=

,...,i

)

w(p

, . . . , p

). (90)

Утверждение 1.24. Имеет место формула для числа объектов, не обладающих никаким свойством:

E(0) = N − W (1) + W (2) − W (3) + . . . + (−1)

W (n). (91)

 Расс мотрим два случая. 1

◦

Пусть x

не обладает никаким свойством. Тогда в лев ую часть формулы он

добавит единицу. А спра ва будем считать, что его единица в ходит в число N. 2

◦

Пусть x

обладает свойствами

, . . . , p

. Тогда вклад в левую часть есть 0. А в правую — 1 − C

+ C

+ . . . + (−1)

= (1 − 1)

= 0. 

2. Кодирование

2.1. Общая теория кодирования и сжатия информации

2.1.1. Схемы кодирования. Коды с однозначным декодированием

Пусть заданы два алфавита A = {a

, . . . , a

} и B = {b

, . . . , b

Определение. Слово в каком-либо алфавите — это конечный упорядоченный набор символов этого алфа-

вита. Множество всех слов алфавита A мы будем обозначать A

∗

Определение. Схема кодирования — это любое отображение ϕ : A → B

∗

, ϕ : a

7→ B

. Образ символа при

таком отображении будем называть кодом этого символа.

Такое отображение очевидным образом распространяется на множество всех слов над алфавитом A:

. . . a

7→ B

. . . B

. (1)

Пример 1.1. A = {a

, a

}, B = {0, 1}. Схему кодирования зададим следующим образом:

7→ 01, a

7→ 010, a

7→ 101. (2)

Исходному слов у a

будет соответствовать кодовое слово 0101 01.

Определение. Будем говорить, что некоторая схема кодирования допускает однозначное декодирование, ес-

ли кодовые слова (то есть результаты кодирования) различны для любых несовпадающих кодируемых наборов.

Нетрудно заметить, что схема кодирования в предыдущем примере не допускает однозначного декодирова-

ния, так как кодовое слово 010101 соответствует одновременно двум наборам — a

и a

2.1.2. Неприводимые слова

Определение. Префиксной называют такую схему кодирования, в которой код ни одного из символов вход-

ного алфав ита не является началом для кода другого символа.

Замечание. Это условие является достаточным для однозначности декодирования, но не необходимым. В

качестве примера можно рассмотреть схему a 7→ 0, b 7→ 01 . Ясно, что это не префиксный код, но тем не менее

декодирование однозначно.

Определение. Слово, допускающее неоднозначное декодирование, наз ывают неприводимым , если при уда -

лении из него каких-либо символов полученное слово либо не является кодовым (то ест ь не допускает декоди-

рования вообще), либо допускает только однозначное декодирование.

Очевидно, что любой код, допуска ющий неоднозначное декодирование, содержит неприводимые слова.

Определение. Рассмотрим некоторое кодовое слово b

. . . b

, допускающее неоднозначное декодирование.

Схематически это можно изобразить следующим об разом:

Рис. 6. Примеры слов

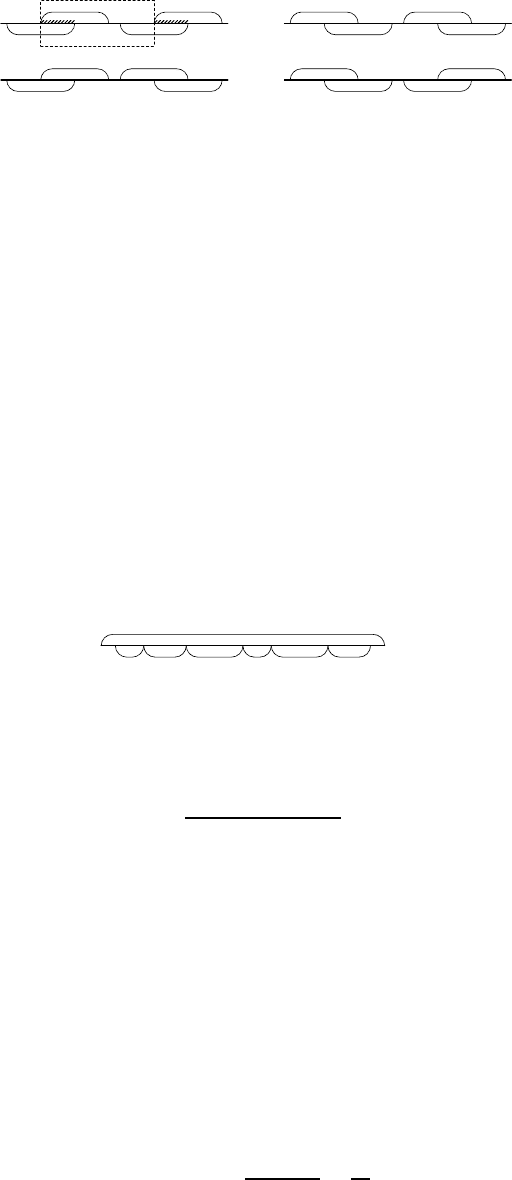
Рассмотрим разбиение, полученное объединением верхнего и нижнего ра з биений, получим набор отрезков.

Если отрезок одного декодирования целиком содержится в некотором отрезке другого (как a

и a

на на-

шей схеме), его на з ы вают отрезком первого рода, иначе, то е сть если он является началом отрез ка при одном

декодировании и концом при другом (как пересечение отрезков a

и a

на рисунке) — отрезком второго рода.

Лемма 2.1 (О неприводимом слове). В неприводимом слове все отрезки второго рода различны.

 Предположим противное: пусть нашлось два одинаковых отрезка второго рода. Имеются четыре воз-

можности их расположения:

а)

б)

в)

г)

Рис. 7. Возможные расположения верхних и нижних слов

Разберем случай а), а для остальных случаев рассуждения аналогичны. Совпадающие отрезки второго рода

выделены штриховкой. Удалим из слова все символы от начала первого отрезка до начала второго, и «склеим»

оставшиеся слова. Полученное таким образом сло во также будет допускать неоднозначное декодирование, а это

противоречит предположению о том, что исходное слово было неприводимым. 

2.1.3. Проверка однозначности декодирования

Мы хотим получить алгоритм проверки однозначности декодирования. Именно, эта процедура будет выгля-

деть примерно так: проверяем однозначность декодиро вания кодов, полученных из слов алфавита A длины не

более N , где N зависит только от схемы кодирования, и если это так, то заключаем, что и вся схема однозначна.

Рассмотрим следующую схему кодирования: исходный алфавит A = {a

, . . . , a

}, конечный алфавит B, со-

стоящий из q символов, причем каждому символу a

∈ A ставится в соответст вие слово B

∈ B

∗

длины l

Обозначим l := l

+ . . . + l

Ясно, что нужно проверять только неприводимые слова. Сейчас мы покажем, что длина неприводимого

слова ограничена константой. Её-то и возьмём в качестве числа N .

Зафиксируе м некоторое слово и его код, и мы хотим выяснить, может ли этот код быть неприводимым

словом. Вначале убедимся, что оно допускает по крайней мере два декодирования. Потом выпишем оба деко-

дирования, как на рис. 6.

Под кодовым словом (или просто сло вом) будем понимать код симв ола. Посчитаем максимальное число

кодовых слов одного декодиров ания, которые одновременно попадают внутрь некоторого слов а другого деко-

дирования (см. рис. 8)

Рис. 8. Слов´а внутри другого сл´ова

. Обозначим эту величину через w.

Утверждение 2.2. Максимальная длина самого короткого слова в алфавите A, порождающего (при ука-

занной выше схеме кодирования) неприводимое слово над алфавитом B, не превосходит величины

N =

(1 + l − r)(w + 1)

. (3)

 Рассмотрим первое длинное (не содержащееся ни в каком другом) слово. Все остальные длинные слова

начинаются с о трезков второго рода. Обозначим число длинных сло в через R, а число отрезков второго рода —

через k. Получим R = 1+k. Общее число слов, лежащих внутри других, не превосходит Rw, а число не лежащих

внутри (то есть длинных) — в точности равно R. Значит, всего не более Rw + R = R(w + 1) = (1 + k)(w + 1) слов.

Осталось оценить k. Заметим, что любой отрезок второго рода является началом некоторого длинног о слова.

Сколько может быть «начал»? Слово B

длины l

имеет l

−1 начало. Если рассматриваемое декодируемое слово

неприводимо, все отрезки второго рода должны быть различны, значит,

k 6

i=1

− 1) = l − r, (4)

откуда получаем N 6 (1 + l − r)(w + 1). Здесь N = N

+ N

— число слов в обоих декодированиях. Осталось

заметить, что

min(N

, N

) 6

+ N

, (5)

и мы приходим к требуемой оценке. 

2.1.4. Неравенство Мак-Миллана

Напомним, что мы обозначаем через q количество букв в алфавите B.

Утверждение 2.3 (Неравенство Мак-Миллана). Если кодирование допускает только однозначное де-

кодирование, то

+ . . . +

6 1. (6)

 Обозначим l := max

. Пусть Q(n, t) — число кодовых слов длины t, которые являются образами слов

длины n (вполне возможно, что какие-то Q(n, t) равны нулю). Рассмотрим



+ . . . +



,...,i

)

· . . . · q

t=1

Q(n, t)

. (7)

Переход, отмеченный «!» следует в точности из того, что схема однозначно декодируется, и потому имеется

инъективное соответствие

, . . . , i

) 7→ a

. . . a

7→ B

. . . B

. (8)

Всего имеется q

слов длины t, поэтому во всяком случае Q(n, t) 6 q

, следовательно



+ . . . +



6 ln, (9)

откуда

+ . . . +

√

ln. (10)

Переходя к пределу при n → ∞, получаем неравенство (6). 

Теорема 2.4. Для любой схемы кодирования B, имеющей однозначное декодирование, найдется префиксная

схема

B, имеющая тот же набор длин слов, что и схема B.

 Упорядочим по возрастанию длины l

кодовых слов из B, то есть будем считать, что l

6 . . . 6 l

. Пусть

набор {λ

} — это отсортированный по возрастанию набор {l

}, из которого выкинуты дубликаты (и таким

образом, λ

< . . . < λ

), а ν

— количество дубликатов длины λ

В этих обозначениях (собирая одинаковые слагаемые) нераве нство Мак-Миллана переписыв ается следующим

образом:

+ . . . +

6 1. (11)

Будем ст роить новую схему

B последовательно. Для начала включим в неё ν

различных слов длины λ

Это не противоречит её префиксности. В силу условия оптимальности, в ней должно быть ещё ν

слов длины

. Чтобы префиксность не нарушилась, мы можем брать не любые слова длины λ

, коих всего имеется q

штук, а только те, которые не начина ются с уже выбранных. Таких имеется ν

·q

−λ

штук, потому что каждое

из первых ν

кодовых слов можно расширить до слова длины λ

именно q

−λ

способа ми. Таким образо м,

остаётся не более q

− ν

· q

−λ

кодовых слов. Но их хватит, потому что их нужно ν

штук, то есть должно

быть выполнено неравенство ν

6 q

− ν

· q

−λ

. А его можно переписать по-другому:

6 1. (12)

А это уже прямое следствие неравенства (11). Значит, нужное количество слов длины λ

тоже найдётся. Далее,

при выборе слов длины λ

нам запреще но ν

· q

−λ

+ ν

· q

−λ

слов, но, опять-таки в силу неравенства (11)

мы их найдём, и так далее.

В итоге мы получи префиксный код

B, у которого набор длин кодовых слов тот же. 

Следствие 2.1. При рассмотрении любой схемы кодирования всегда можно считать, что она префиксная.

2.1.5. Оптимальные коды. Код Хаффмана

Как и рань ше, рассматриваем следующую схему кодирования: исходный алфавит A = {a

, . . . , a

}, конечный

алфавит B, состоящий из q символов, причем каждому символу a

ставится в соответствие слово B

длины l

Теперь наша цель — построить в некотором смысле оптимальный код. Пусть мы кодируем некоторый текст

(последоват е льность символов исходного алфавита). Ясно, что если какие-то символы очень часто встречаются

в э том тексте, то будет хорошо, если кодовые слова, им соо тветст вующие, будут иметь маленькую длину, и

наоборот. Будем считать, что нам известны вероятности p

появления в тексте кодируемых символов a