Лупанов О.Б. Курс лекций по дискретной математике

Подождите немного. Документ загружается.

Пришло время использовать полученную для N

′′

оценку. Далее все неравенства записаны для достаточно боль-

ших n:

log N

′′

, n) − 2

+ o(1) 6 (h

+ n) log



C(h

+ n)



− 2

+ o(1) 6



(1 − ε)

+ n



n − 2

+ o(1) = (1 − ε)2

+ n

− 2

+ o(1) =

= n

+ o(1) − ε2

→ −∞, n → ∞, (20)

что и требовалось доказать. 

3.2. Инвариантные классы

В логике для множества всех булевых функций от n переменных используется обозначение P

(n). Множеств о

всех булевых функций обозначается через P

Определение. Множество K ⊂ P

(n) называе тся инвариантным классом, если оно замкнуто относительно

подстановок констант, переименования переменных (без отождествления) и до бавления/отбрасывания несуще-

ственных переменных.

Пример 2.1.

• Очевидно, P

является инвариантным классом.

• Функции, существенно зависящие не более чем от k переменных, образуют инвариантный класс.

• Линейные и монотонные функции образуют инвариантный класс.

Пусть Q — инвариантный клас с . Через P

(n) будем обозначать количество функций из Q от n переменных.

Ясно, что P

(n) 6 2

Будем считать, что Q 6= ∅. Рассмотрим последовательность

(n). (21)

Утверждение 3.4. Последовательность {q

} монотонно убывает (нес трого).

 Возьмём функцию f ∈ Q, зависящую от n + 1 переменной и разложим её по последней переменной:

f(x

, . . . , x

n+1

) = x

n+1

f(x

, . . . , x

, 1) ∨ x

n+1

f(x

, . . . , x

, 0). (22)

Имеем f(x

, . . . , x

, c) ∈ Q, где c = 0, 1. Итак, каждая функция от n+1 переменной может быть сконструирована

из двух функций от n переменных этого же класса. Стало быть, число функций от n+ 1 переменных из Q никак

не больше, чем число пар функций из Q от n переменных. Итак,

(n + 1) 6 P

(n)

. (23)

Извлекая из этого неравенст ва корень степени 2

n+1

, по лу чаем

n+1

(n + 1) 6

n+1

(n)

(n) = q

, (24)

что и требовалось доказать. 

С другой сторо ны, ясно, что q

> 1 при всех n (так как Q 6= ∅ и пот ому P

(n) > 1). Значит, существует

предел у этой последовательности.

Определение. Число

σ(Q) := log lim

n→∞

(25)

называет ся параметром инвариантного класса.

Поскольку 1 6 q

6 2, получаем, что σ(Q) ∈ [0, 1]. Сейчас мы докажем, что P

— единственный инвариантный

класс с параметром 1.

Утверждение 3.5. σ(Q) = 1 ⇔ Q = P

 Справа налево — очевидно. Обратно, пусть Q 6= P

. Значит, в нём нет какой-либо функции от m пере-

менных. Стало быть, P

(m) < 2

, и потому q

< 2. Но эта последовате льность убывает, поэтому и предел не

может быть равен 2. 

Замечание. Можно доказать, что для каждого σ 6= 1 существует континуум инвариантных классов с пара-

метром σ. Это нетривиальная тео рема, мы не будем её здесь доказывать.

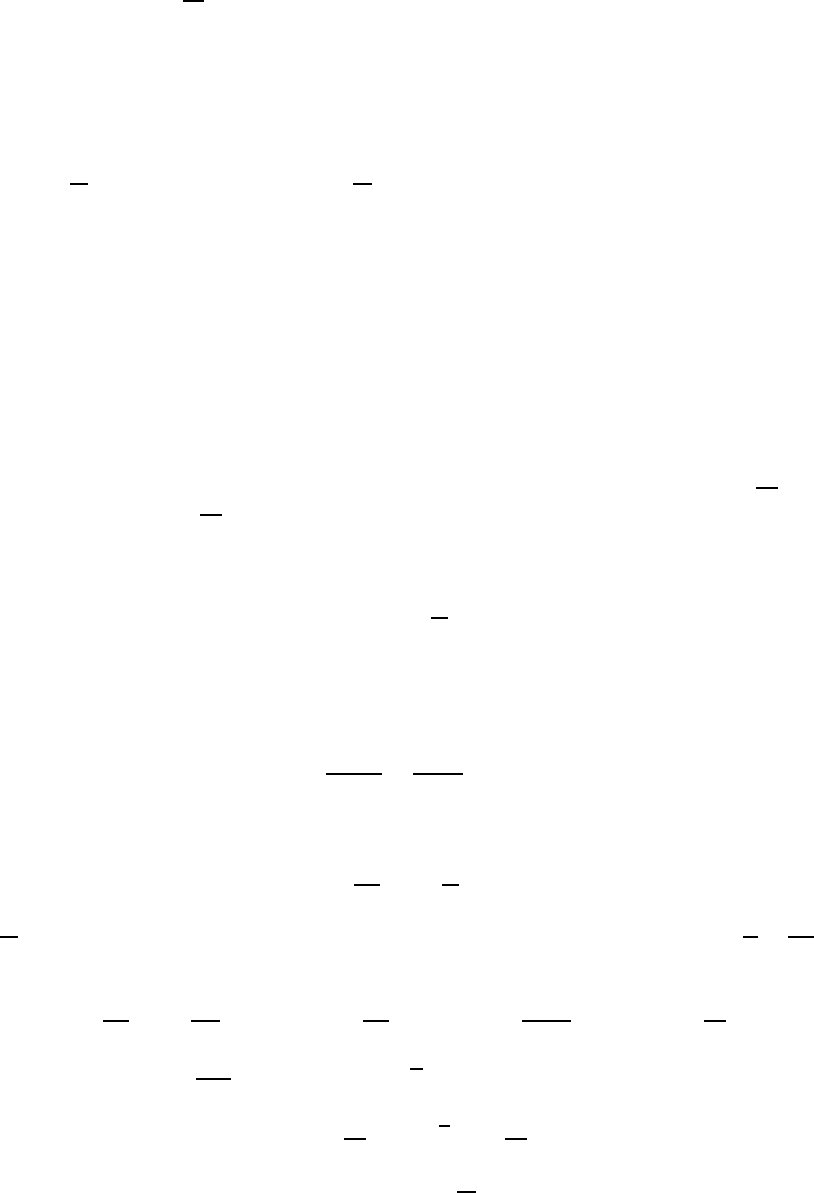
Так как lim q

= 2

, то q

= 2

(1 + ε

), где ε

→ 0. Логарифмируя это равенство, получаем

log P

(n) = σ + δ

, δ

:= lo g(1 + ε

) → 0. (26)

Умножая на 2

обе части, имеем

log P

(n) = 2

σ + 2

. (27)

Если σ 6= 0 , то главный член этой последов ательности определяется первым слагаемым, и log P

(n) ∼ σ · 2

Если же σ = 0, то log P

(n) = o(2

Теорема 3.6. Имеет место асимптотическая оцен ка сложности функций из класса с параметром σ: если

σ 6= 0, то L(f) . σ ·

, а если σ = 0, то L(f ) . o





 Будем нумеровать функции из нашего класса последоват е льностями нулей и единиц. Я с но, что для

нумерации всех функций от n переменных из Q достаточно брать l

:= ⌈log P

(n)⌉ двоичных разрядов. Итак,

∼ σ · 2

, а при σ = 0 имеем l

= o(2

Возьмём какую-либо функцию f ∈ Q от n переменных, выберем k < n и обозначим m := n −k. Положим l :=

для краткости. Оставим первые k переменных, а вместо ос тальных будем подставлять константы α

k+1

, . . . , α

При подстановке констант будем получать функции от k аргументов, которые тоже лежат в Q, пос кольку это

инвариантный клас с. Каждой такой функции f (x

, . . . , x

, α

k+1

, . . . , α

) соответствует какой-то номер. Итак,

для фиксированной функции f получаем отображение нумерации

ϕ: (α

k+1

, . . . , α

) 7→ (τ

, . . . , τ

). (28)

А теперь построим схему Φ, которая реализует это от ображение. Нам нужно построить l функций, каждая

из которых зависит от m аргу ментов x

k+1

, . . . , x

. Значит, на каждую функцию уйдёт порядка

элементов, а

всего на схему Φ уйдёт порядка l ·

элементов.

Через ∆ обозначим схему, которая будет по номеру функции f(x

, . . . , x

, α

k+1

, . . . , α

), то есть по набору

(τ

, . . . , τ

), генерировать её таблицу значений. Эта схема будет иметь l входов и 2

выходов, поэтому

L(∆) . 2

. (29)

К эт ому декодеру подключим схему Σ, которая получает на вход набор (α

, . . . , α

) и таблицу истинности

функции от k переменных (т у са мую, которую выдаёт декодер ∆), а на выходе даёт значение этой функции на

наборе (α

, . . . , α

). Схема Σ имеет 2

+ k входов, поэтому её сложность имеет порядок

L(Σ) .

+ k

= 2

. (30)

Теперь считаем сложность агрегата, полученного соединением ∆, Φ и Σ. (обозначим его F ). Соединяя полу-

ченные выше оценки, получаем

L(F ) . l ·

+ 2

. (31)

Функция

монотонно в озрастает при больших x, поэтому в силу того, что l 6 2

, имеем

◦

. Пусть σ 6= 0. Тогда имеем l ∼ σ · 2

, и потому

L(F ) . σ · 2

+ 2

= σ · 2

+ 2 · 2

= σ ·

n − k

+ 2 · 2

. σ ·

+ 2 · 2

. (32)

Волевым решением полагая k :=

log n

, получаем 2

√

n, поэтому

L(F ) . σ ·

+ 2 · 2

√

. σ ·

. (33)

◦

. Если σ = 0, то аналогично показывает ся, что L(F ) . o





. 

Следствие 3.2 (С. В. Яблонский). Пусть f

, . . . , x

) — самая сложная функция от k переменных,

то есть L(f ) = L(k). Рассмотрим множество функций F := {f

}

∞

i=1

. Тогда замыкание [F] относительно

подстановки констант даст все булевы функции.

 К сожалению, мы не можем утверждать, что [F] — инвариантный кла с с, поскольку априори неясно,

что он замкнут относительно добавления и удаления несущественных переменных. Однако мы в идим, что в

нём (по построению) есть функции от любого числа переменных и потому для него тоже можно корректно

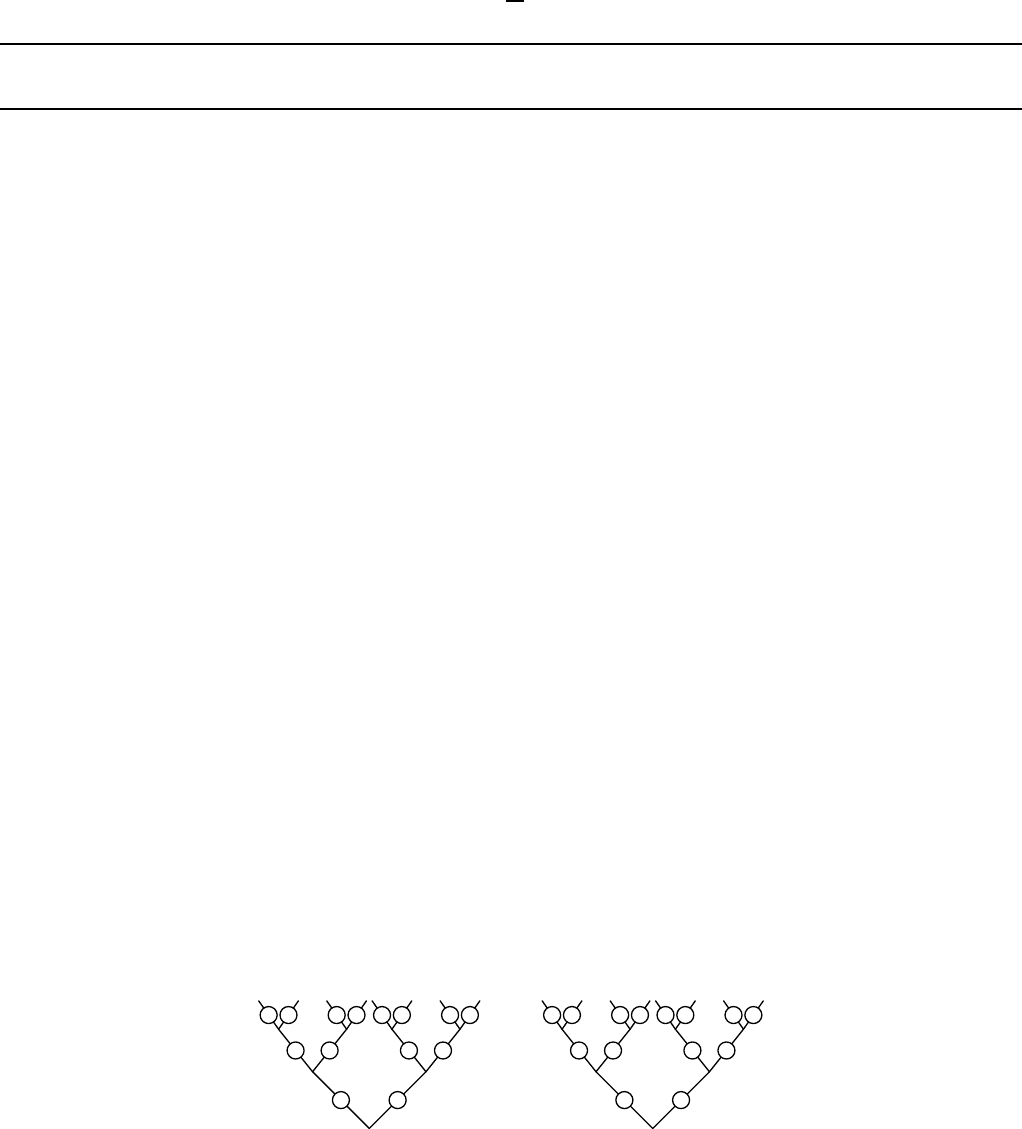
определить параметр σ (пройдёт рассуждение с ограниченностью снизу последовательности q

). Доказанная

только что теорема вовсе не использует данное свойство инвариантных классов, поэтому она справедлива и

для [F]. Осталось заметить, что никакие значения параметра, кроме 1, для [F] не подходят, потому что иначе

асимптотическая сложность была бы строго меньше

, а у нас есть все самые сложные функции. Значит,

параметр множества [F] равен 1, а потому [F] = P

. 

Было ещё сказано, что «если допустить отождествление переменных, то инвариантных классов не будет». Почему это так, и в

каком смысле это надо понимать, неясно, потому что, например, из линейных функций даже используя отождествление переменных,

ничего лучше линейных функций получить нельзя.

4. Теория автоматов

4.1. Автоматы

4.1.1. Детерминированные функции

Рассмотрим два алфавита A = {a

, a

, . . . , a

}, B = {b

, b

, . . . , b

} и фу нкции вида f : A

∞

→ B

∞

, то е сть

функции, преобразующие бесконечные последовательности букв алфавита A в бесконечные последовательности

букв алфавита B.

Пример 1.1. Пусть f переводит последовательность, состоящую сплошь из нулей, в себя, а все остальные —

в последовательност ь, состоящую сплошь из единиц. Для такой функции су ществует последовательность —

состоящая лишь из нулей, для которой невозможно определить её образ, зная лишь конечное число членов. Это

причиняет неудобства при вычислении, поэтому введём понятие детерминированности.

Мы будем обозначать символы входной последовательност и через a(t), где t = 1, 2, 3, . . ., а выходной после-

довательности — через b(t).

Определение. Функция f : A

∞

→ B

∞

называет ся детерминированной, если b(t) однозначно определяется

первыми t членами входной последовательности a(1), a(2), . . . , a(t).

Пример 1.2. Детерминированными функциями являются:

• Функция



0, . . . , 0, 1

, ?, . . . , ?, . . .



7→



0, . . . , 0, 1

, 1, . . . , 1, . . .



. Здес ь «?» — любой символ.

• Функция чётности b(t) = a(1) ⊕ . . . ⊕ a(t);

• Функция единичной задержки



a(1), a(2), . . . , a(t), . . .



7→



0, a(1), a(2), . . . , a(t − 1), . . .



;

• Функция b(t) =

(

1, t = 2

;

0, t 6= 2

Без ограничения общности можно считать, что входной алфавит состоит из двух символов: 0 и 1. Тогда

детерминированные фу нкции можно задавать на бинарных деревьях. Бинарное дерево — это дерево с корнем,

такое что из каждой вершины выходит 2 ребра, и в о все вершины, кроме корня, входит одно реб ро. Каждой

бесконечной двоичной последоват е льности пос тавим в соответ с твие определённый путь на дереве: движение

начинается из начальной вершины, и ес ли a(i) = 0, то идём по левой ветке, а если a(i) = 1, то по прав ой. При

этом очередному зве ну пути приписываем значение b(i). Легко видеть, что такое соответ с твие осуществляет

биекцию между деревьями и детерминированными функциями.

Пример 1.3.

0 1

0 1 1 0

0 1 1 0 1 0 0 1

0 1

0 1 1 1

0 1 1 1 1 1 1 1

Рис. 10. Деревья детерминированных функций

Деревья на рис. 10 иллюстрируют первые два примера детерминированных функций, приведённых выше.

Можно было бы и не ограничивать выходной алфавит двумя символа ми. Тогда вместо бинарных деревьев

следовало бы рассматривать деревья, у которых из каждой вершины растёт по µ веток.

4.1.2. Автоматы

Определение. Ограниченно детерминированные функции (конечные автоматы) — детерминированные

функции, деревья которых содержат лишь конечное число различных поддеревьев.

Замечание. Слово «конечный» в названии «конечный автомат» часто опускают. Мы тоже будем это делать,

всегда подразумевая конечный автомат.

Пронумеруем различные поддеревья. Номера будем писать в начальных вершинах поддеревьев.

Пример 1.4.

1 0

0 1

Рис. 11. Поддеревья функции чётности

Рассмотрим снова функцию чётности. Её дерево содержит только 2 вида поддеревьев. Эту диаграмму надо

понимать так: если мы находимся в дереве №1 и на входе 0, то выход — 0 и мы остаёмся в дереве №1, а если на

входе 1, то выход — 1 и мы переходим в дерево №0. Аналогично для дерева №0.

В общем случае, если речь идёт о конечно детерминированных ф ункциях, можно утверждать, что достаточно

знание конечного числа конечных фрагментов дерева, чтобы найти образ любой последовате льности.

Определение. Номера поддеревьев называются состояниями автомата.

Фрагменты дерева могут задаваться диаграммами переходов (диаграммами Мура). Они представляют собой

ориентированные графы, вершины которых соо тветствуют состояниям, а каждому ребру приписывается пара

символов, первая компонента которой соответствует входу, а вторая — выходу. Направление ребра соответствует

переходу из одного состояния в другое.

Пример 1.5. Диаграмма Мура для функции чётности (см. рис. 12).

0 1

(1, 1)

(1, 0)

(0, 0) (0, 1)

Рис. 12. Диаграмма Мура функции чётности

Автомат можно задавать функцией перехода q(t + 1) = G



a(t), q(t)



и функцией выхода b(t) = F



a(t), q(t)



Здесь q(t) — состояние в момент t. Удобно считать q(1) = 0. Эти три уравнения называются уравнениями

автомата.

Пример 1.6.

0 1

(1, 0)

(0, 1)

(0, 0) (1, 1)

Рис. 13. Диаграмма Мура функции единичной задержки

Найдём уравнения автомата единичной задержки, т. е. функции с выходом b(1) = 0, b(t) = a(t − 1), t > 1.

Построим диаграмму Мура (см. рис. 13). По ней видно, что q(t + 1) = a(t), а b(t) = q(t). При этом q(1) = 0.

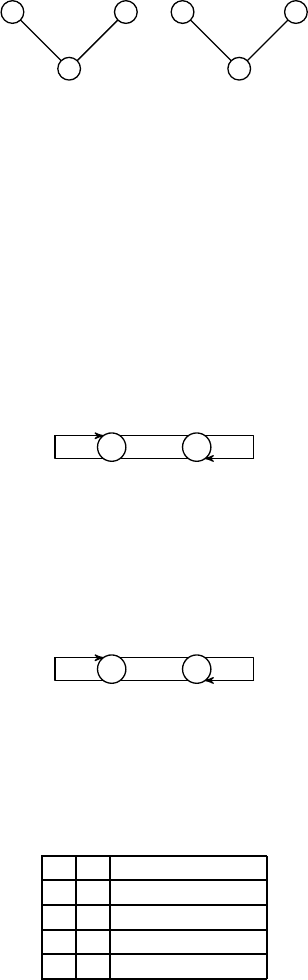
Можно также задавать диаграммы функций таблицами. Например, функция единичной задержки зада ё тся

следующей таблицей:

a q F (a, q), G(a, q)

0 0 (0, 0)

0 1 (1, 0)

1 0 (0, 1)

1 1 (1, 1)

Теорема 4.1. Любой автомат можно реализовать СФЭ, используя элементы 4 видов: конъюнкцию, дизъ-

юнкцию, отрицание и функцию един ичной задержки.

 Пусть автомат работает на алфав итах A и B и имеет λ состояний. Положим n :=



log |A|



, m :=



log |B|



Занумеруем буквы A и B двоичными последоват е льностями длины n и m соо тветственно. Состояния автомата

, . . . , q

λ−1

также занумеруем двоичными последовательностями длины l :=



log



, причём q

соотв е тствует

(0, . . . , 0). Введём новые функции перехода и выхода, определённые уже н а наборах из 0 и 1:

(



(t), . . . , β

(t)





(t), . . . , α

(t), ω

(t), . . . , ω

(t)





(t + 1), . . . , ω

(t + 1)





(t), . . . , α

(t), ω

(t), . . . , ω

(t)



(1)

Рис. 14. Автомат

Каждая из компонент векторов

β и eω реа лизуется некоторой булевой функцией (вообще говоря, не всюду

определённой). Построим СФЭ, совместно реализующую все эти функции (обозначим их через f

, . . . , f

, . . . , g

Соединим выходы g

, . . . , g

через элементы единичной задержки (они показаны на рис. 14 прямоугольни-

ками) с входами ω

. . . ω

. Очевидно, что такая схема будет работать согласно приведённым выше уравнениям

автома та (при условии, что элементы единичной задержки в первый момент времени выдают нули). 

Обратное также верно: любая СФЭ типа той, что была рассмотрена выше, моделирует некоторый автомат.

4.2. Регулярные события. Теорема Клини

4.2.1. Регулярные события

Пусть, как и раньше, мы рассматриваем конечные автоматы с алфавитами A и B. Зафиксируем некоторое

подмножество B

′

⊂ B.

Определение. Рассмотрим слово w := a(1), . . . , a(t), поданное на вход конечного автомата. Будем гово рить,

что слово w принято автоматом, если b(t) ∈ B

′

. Множество всех слов, принимаемых автоматом, будем называть

событием, или представимым данным автоматом.

Мы будем выяснять вопрос о том, можно ли описать все события. Оказывается, это можно сделать, и ответ

будет дан в терминах так называемых регулярных множеств, которые мы сейчас определим.

Для начала нам потребуется несколько вспомогательных определений.

Определение. Конкатенация (склейка) двух сло в w

и w

какого-либо алфавита — это просто сло во w

Определение. Конкатенация M

двух множеств M

и M

— это множество

:= {w

| w

∈ M

, w

∈ M

}. (2)

Конкатенацию множества с самим собой мы будем обозначать в виде степени (не пу тать с декартовой сте-

пенью!). Иначе говоря,

M . . . M

| {z }

k раз

= M

. (3)

Определение. Итерация данного множеств а — это множество

hMi := M ∪ M

∪ M

∪ . . . (4)

Определение. Одноэлементные подмножества алфавита A по определению являются регулярными мно-

жествами. Далее, если M

, M

— регулярные множества, то M

∪ M

, M

и hM

i тоже будем называть

регулярными множествами. Пустое множес тво тоже будем считать регулярным.

Чуть позже мы докажем теорему Клини, которая утверждает, что регулярные множества и представимые

множества — это одно и то же.

4.2.2. Свойства регулярных множеств

Все однобуквенные слова регулярны по определению. Очевидно, что любое конечное множес тво слов регу-

лярно.

Лемма 4.2. Рассмотрим уравнение X = XC ∪ D н а X. Его решение существует и единственно.

 Покажем, что множество F

:= D hCi ∪ D является решением. В самом деле, подставим в уравнение:

(D hCi ∪ D)C ∪ D = D hCiC ∪ DC ∪ D = D hCi ∪ D. (5)

Допустим, что существует како е -либо другое решение F

6= F

, то есть F

= F

C ∪ D.

Пусть сначала F

* F

. Рассмотрим самое короткое слово α ∈ F

r F

. Ясно, что α /∈ D, иначе бы α ∈ F

Стало быть, α ∈ F

C и потому имеет вид α = α

, где α

∈ F

, а α

∈ C. Заметим, что α

∈ F

, иначе α не

было бы самым коротким словом в F

r F

. Но тогда α ∈ F

C ⊂ F

C ∪ D = F

, противоречие.

Пусть теперь F

* F

. Дальнейшие рассуждения абсолютно аналогичны, если поменять ролями F

и F

Возьмём самое короткое α ∈ F

r F

. Ясно, что α /∈ D, иначе α ∈ F

. Отсюда следует, что α ∈ F

C и потому

имеет вид α = α

, где α

∈ F

, а α

∈ C. Но тогда α

∈ F

, иначе α не было бы самым коротким, а тогда

α = α

∈ F

C ⊂ F

C ∪D = F

— противо речие.

Значит, на самом деле F

= F

, то есть решение единственно. 

Следствие 4.1. Если коэффициенты в уравне нии X = XC ∪ D регулярны, то и решение регулярно.

Следствие 4.2. Рассмотрим систему уравнений











= X

∪ X

∪ ··· ∪ X

∪ R

. . .

= X

∪ X

∪ ··· ∪ X

∪ R

(6)

относительно переменных X

, . . . , X

. Если события R

регулярны, то решение системы существует, един-

ственно и также ре гулярно.

 Докажем для случая двух переменных, для случая б´ольшего их числа всё делается аналогично (и по

индукции).

(

= X

∪X

∪ R

= X

∪X

∪ R

(7)

Перепишем второе уравнение так: X

= X

∪ (X

∪ R

) и обо значим второе слагаемое через D, а R

через C. Получаем уравнение X

= X

C ∪D. По лемме у него имеется единственное решение

= D hCi ∪ D = (X

∪ R

) hR

i ∪ (X

∪R

). (8)

Подставим во первое урав нение:

= X

∪ [(X

∪ R

) hR

i∪ (X

∪ R

)]

| {z }

∪ R

. (9)

А теперь раскроем скобки и вынесем X

= X



∪[R

i ∪ R



∪ [R

i ∪ R

∪R

. (10)

Опять полу чилось уравнение, про которое мы уже всё знаем. Осталось заметить, что все коэффициенты регу-

лярны. 

4.2.3. Обобщённые источники. Доказательство теоремы Клини

Рассмотрим автомат с набором состояний q

, . . . , q

, входным алфавитом A = {a

, . . . , a

} и выходным ал-

фавитом B = {b

, . . . , b

}. Рассмотрим подмножество B

′

⊂ B.

Сейчас мы докажем одну половину теоремы Клини.

Утверждение 4.3. Все представимые события регулярны.

 Обозначим через M

множество всех слов , под воздействием которых автомат из состояния q

попадает

в состояние q

. Через M

′

обозначим множество букв, при подаче которых в сос тоянии q

автома т выдаёт букву

из B

′

. Очевидно, что все представимые слова имеют вид

[

i=1

′

. (11)

Поскольку все множества M

′

конечны, они регулярны. Значит, осталось доказать, что в с е множества M

тоже

регулярны.

Пусть R

— множество бу кв, которые переводят ав томат из состояния q

в состояние q

. Множества R

конечны, а потому регулярные.

Выясним, откуда можно прийти в состояние q

. В него можно прийти из M

, если нам дадут букву R

Кроме того, в него можно прийти из M

, но только если нам дадут букву из R

, и так далее . Стало быть,

= M

∪ M

∪ ··· ∪ M

λk

∪ R

. (12)

Последняя возможность соот ветствует тому, что мы сразу попали в q

. Мы видим, что у нас получилась как раз

такая система, про решения которой мы всё знае м — все они регулярные. Итак, первая часть теоремы Клини

доказана. 

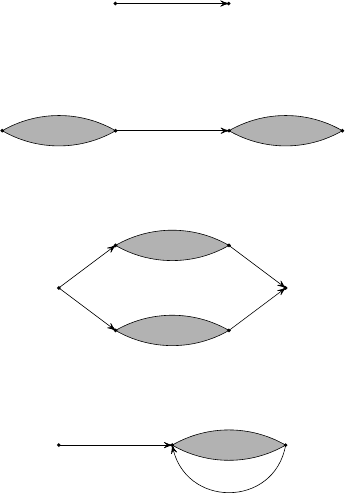
Определение. Обобщённый источник — это ориентированный конечный граф, в котором выделены две

вершины, называе мые началом S и концом E соответственно. Некоторым рёбрам приписаны буквы исходного

алфавита.

По рёбрам источника можно ходить, соблюдая ориентацию. Рассмотрим все пути в графе по рёбрам из S

в E. При этом каждому пути е с тественным образ ом сопоставляется слово из тех букв, которые написаны на

рёбрах. Таким образом, всякий обобщённый источник порождает некоторое множество слов.

Пусть нам дано регулярное событие. Покажем, что можно построить обобщённый источник, который по-

рождает в точно с ти это событие.

Источник, порождающий какую-либо букву, строится тривиально : это одно ребро из S в E, на котором

написана эта буква.

S E

Рис. 15. Генератор одной буквы

Пусть мы умеем строить источники D

и D

для событий M

и M

соотв е тственно. Тогда источник для

события M

делается так, как показано на рис. 16.

S E

Рис. 16. Генератор конкатенации

Для генерации объединения множеств M

∪ M

нужно использовать источник, изображённый на рис. 17.

S E

Рис. 17. Генератор объединения

Наконец, для итераций используется источник, изображённый на рис. 18.

S E

Рис. 18. Генератор итераций

Итак, по регулярному множест ву построен источник. А теперь по исто чнику пост роим а втомат, для которого

данное множес тво является представимым. Пусть V — множе ство вершин источника. Рассмотрим автомат, в ко-

тором состояниями будут подмножества вершин нашего источника. Таким образом, у него будет 2

|V |

состояний.

В качестве выходного алфавита возьмём B := {0, 1}, а B

′

= {1}.

Рассмотрим q

⊂ V . Рассмотрим то множество вершин, в которое мы можем попасть под действием б уквы

из вершин, принадлежащих состоянию q

. Получим какое-то другое подмножество вершин q

. Таким образом

определена функция перехода: G(a

, q

) = q

Осталось определить отображение выхода: если в q

попала вершина E, то при переходе q

−→ q

выдаём

на выход 1, а иначе выдаём 0. Понятно, что такой автомат в случае регулярного события выдаёт единицу, а в

случае нерегулярного — ноль.

Это завершает доказательство обещанной теоремы:

Теорема 4.4 (Клини). Всякое регулярное событие является представим ым, и наоборот.

4.2.4. О том, чего не могут автоматы

В заключение мы докажем теорему о том, что не су ществует никако й конечной полной системы автоматных

функций. Иначе говоря, если разрешить использовать в схе ме вместо {¬ & ∨} любые автоматные функции, но

запретить ориентированные циклы, то не существует такого конечного набора автоматных функций, схемой из

которых можно было бы реализов ать любой автомат.

Лемма 4.5. Пусть есть а в т омат с λ состояниями. Пусть н а вход ему подаётся периодическая последо-

вательность с периодом T . Тогда выходная последовательность периодична с периодом T d, где d 6 λ.

 Пусть автомату в некоторый момент времени t

был подан символ a

. Через T шагов ему снова дадут

символ a

. Возможно, автомат окажется в другом состоянии. Ещё через T шагов он снова окажется c тем же

входным симво лом, и так далее. Число состояний равно λ, поэтому не более чем через λ таких циклов (обозначим

это количество через d) он по принципу Дирихле дважды побывает в одним и том же состоянии. Начиная с

этого момента всё повторится, а значит, и выход автомата будет периодическим с указанным периодом. 

Через S

будем обозначать множество периодических последовательностей, у которых длина минимального

имеет среди своих простых делителей лишь числа не больше l.

Следствие 4.3. Пусть на вход автомата c не более чем l состояниями подаётся последовательность из

. Тогда н а выходе тоже будет последовательность из S

Следствие 4.4. Пусть есть схема из автоматных функций, каждая из которых имеет не более l состо-

яний. Если на вход подаётся последовательность из S

, то на выходе будет последовательность из S

Замечание. У всей схемы состояний, конечно, может быть будет гораздо больше, но простые делители

периодов всё равно не будут превосходить l.

Теорема 4.6. Не существует конечной полной системы автоматных функций.

 Допустим, что она существует: F

, . . . , F

. Пусть λ

— количество состояний ав томата F

. Пусть l :=

max λ

. Рассмотрим автомат, выдающий последовательность (вне зависимости от входных данных)

(0, . . . , 0, 1

| {z }

, 0, . . . , 0, 1

| {z }

, . . . ), (13)

где p — простое число, б´ольшее l. Будем на вход подавать сплошные нули (очевидно, это по с ледоват ельность из

). По доказанному выход любого авт омата, построенного на базисе {F

}, должен быть из S

, а у этого автомата

это не так. Противоречие. 