Лупанов О.Б. Курс лекций по дискретной математике

Подождите немного. Документ загружается.

Определение. Стоимостью схемы кодирования B на з овём величину

L(B) :=

i=1

. (13)

Интуитивно яс но, что чем меньше «стоит» схема, тем она эффективнее.

Обозначим l := min

. Из неравенства Мак-Миллана следует, что q

> r.

Рассмотрим равномерную схему кодирования, в которой все кодовые слова имеют одинаковую длину (то есть

фактически просто занумеруем буквы исходного алфавита в q-ичной системе счисления). Ясно, что нам хватит

длины l =



log



. Такой код обозначим B

. Этот код однозначно раскодируется, и, очевидно, L(B

) = l.

Теорема 2.5 (О существовании оптимального кода). Пусть p := min p

. Если в коде B имеетс я слово

длины l

, то L(B) > L(B

 В самом деле,

L(B) =

> p

> l = L(B

). (14)

Таким об разом, не имеет смысла рассматривать коды с длинами слов больше

, так как равномерный код

будет в этом случае оптимальнее. Но таких кодов (для данного алфавита) конечное число, а потому среди них

существует минимум. 

Определение. Оптимальный код — код с наименьшей стоимостью среди однозначно декодируемых.

Как уже отмечалось в следствии 2.1, оптимальный код можно считать префиксным.

Лемма 2.6. Если B — оптимальный код, то в нём l

6 l

при p

> p

 Докажем от противного. Пусть в коде B нашлись i и j, для которых имеем p

> p

, но l

> l

. Построим

код B

′

путём перестановки в коде B слов B

и B

, получим код с меньшей стоимостью. Против оречие. 

Далее будем считать, что q = 2. Иначе говоря, будем рассматривать только двоичные коды, и выходной

алфавит будет сост оять из двух символов: B = {0, 1}.

Лемма 2.7. В оптимальном коде самое длинное слово не может быть единственным.

 Допустим, что существует единственное максимальное слово. Уберём из него последний символ. Код

префиксный, следовательно полу ченный код также будет однозначным и при этом более эффективным, чем

исходный. Противоречие. 

Лемма 2.8. В оптимальном коде среди слов максимальной длины найдутся два, различающиес я только в

последнем (самом правом) разряде.

 Предположим, что все самые длинные слова различаются не только в последнем разряде. Это означает,

что путём вычеркивания из самых длинных слов этого последнего разряда мы получим однозначный код,

который будет эффективнее предыдущего. 

Рассмотрим оптимальный код B и упорядочим вероятности p

: p

> . . . > p

. В силу леммы 2.6 имеем

6 . . . 6 l

Пусть p

= q

′

+ q

′′

, причем p

> q

′

, p

> q

′′

, и для определённости, q

′

> q

′′

. Для алф авита

A с набором

вероятностей p

> . . . > bp

> . . . > p

> q

′

> q

′′

построим код

B :=



, . . . ,

, . . . , B

, B

0, B



. (15)

Здесь крышки в последовательнос ти обоз начают пропуск элемента, а черта сверху показывает, что слово полу-

ченное склейкой нескольких слов.

Теорема 2.9.

B является оптимальным кодом для заданного набора вероятностей.

 Будем доказывать от противного. Прежде всего заметим, что

B) =

i6=k

+ q

′

+ 1) + q

′′

+ 1) =

i6=k

+ (q

′

+ q

′′

+ (q

′

+ q

′′

) =

+ p

= L(B) + p

. (16)

Пусть

C — оптимальный код, отличный от

B и более эффективный, то есть L(

C) < L(

B). Вы делим в нём

два самых длинных слова, различающихся только в последнем разряде (такие найдутся в силу леммы 2.8) и

обозначим их C

′

и C

′′

. Можно считать, что C

′

= C0, C

′′

= C1. Восстановим по нему код

C := {C

, . . . , C

k−1

, C, C

k+1

, . . . , C

} (17)

для исходного набора вероятностей. Тогда, очевидно, L(

C) = L(C) + p

. Тогда

L(C) + p

= L(

C) < L(

B) = L(B) + p

, (18)

откуда получаем, что L(C) < L(B), что неверно, поскольку код B был оптимальным. 

Теперь ясно, как выглядит процесс построения оптимального кода. Упорядочиваем символы по вероятности

их появления в тексте (по убыванию). Далее берём два са мых редких, складыв аем их вероятности, и полученную

сумму вставляем в упорядоченный набор вероятностей без двух последних элементов. З атем эту процедуру

повторяем, пока не придём к двум вероятностям. Им соответствуют коды 0 и 1. А теперь идём назад: находим

те две вероятности на предыдущем шаге, которые дали в сумме одну из вероятностей p

, им присваиваем коды

K0 и {K1} (добавляем 0 и 1 к уже имеющемуся коду K вероятности p

). И так далее: находим на предыдущем

шаге две вероятности, давшие в сумме одну из имеющихся на данном шаге вероятностей, и приписываем к их

кодам нуль и единицу. Остальные коды переносим в предыдущий шаг без изменений.

Набор кодовых слов для исходного набора вероятностей (то есть то, что получится после возвращения к

первому шагу) и есть код Хаффмана.

2.2. Коды с исправлением ошибок

2.2.1. Постановка задачи

Пусть требуется передат ь по зашумлённому ка налу связи некоторое сообщение (конечный набор симво-

лов фиксированного алфавита). При этом зашумлённость подразумевает возможность искажения некоторых

передаваемых символов. Мы будем передавать сообщение в закодированном виде, при этом добавляя в него

некоторую избыточную информацию с тем чтобы адреса т имел возможность правиль но раскодировать наше

сообщение.

При этом мы будем считать, что в процесс е передачи данных происходят т олько ошибки замещения, то есть

один или несколько с имволов сообщения изменяются на какие-то другие символы, но длина сообщения при этом

не меняется.

2.2.2. Коды Хемминга

Определим схему кодирования для (двоичного) кода Хемминга, исправляющего одну ошибку. Поскольку мы

оперируем с двоичными разрядами, суммирование везде будет предполагаться по модулю два.

Пусть требуется закодировать некоторое сообщение a

. . . a

, где a

∈ B.

Через V

обозначим набор индексов, имеющих в двоичной записи единицу в k-м разряде.

Теперь будем с троить кодовое слово b

. . . b

по следующему правилу. Вначале все разряды с номерами,

не являющимися степенями двойки, заполним символам кодируемого сообщения и назовём информационными.

Разряды с номерами, являющимися степенью двойки, заполним так:

m6=2

,m∈V

. (19)

Такие разряды на з ы вают контрольными. Таким образом, мы выбираем их так, чтобы сумма всех разрядов с

индексами из каждой последовательности V

была равна нулю, потому что в каждом множе стве V

находится

ровно один контрольный разряд. Несложно з аметить, что число контрольных разрядов в кодо вом слове длины n

будет равно m, где 2

m−1

6 n < 2

. Следовательно, число информа ционных разрядов равно n−m, а общее число

наборов длины n в коде Хемминга равно 2

n−m

, потому что мы имеем право заполнять только информа ционные

разряды, а контрольные уже однозначно определяются.

Пусть произошла ошибка в разряде b

. Поскольку код двоичный, то, чтобы исправить эту ошибку, достаточно

знать только номер i. Найдём числа ε

m∈V

. Заметим, что ε

= 0 тогда и только тогда, когда i ∈ V

. Иными

словами, это означает, что последоват е льность ε

. . . ε

есть не что иное, как дво ичная запись числа i. Если мы

получили нулевое число, то ошибок нет.

2.2.3. Свойства кодов, исправляющих ошибки

Определение. Расстоянием Хемминга между двумя кодовыми словами будем наз ывать число различных

разрядов в них. Минимальным расстоянием кода C будем называть, соответст венно, минимум таких расстояний

по всем парам слов из C.

Определение. Весом Хемминга кодового слова будем называть число ненулевых символов в нём.

Замечание. Это определение работает не только для двоичных кодов, но и для кодов над Z

Сейчас мы выясним, что такое вообще двоичный код C, который испра вляет одну о шибку. Пусть α, β ∈ C.

Введём на булевом кубе, в который вложен наш код C, метрику, задаваемую расстоянием Хемминга. Шары

радиуса 1 с центрами в точках α и β не должны пересекаться, иначе возможна ситуация, когда искажённое

слово попадёт в «сферу влияния» двух кодовых слов, и будет неясно, к какому из двух слов его относить.

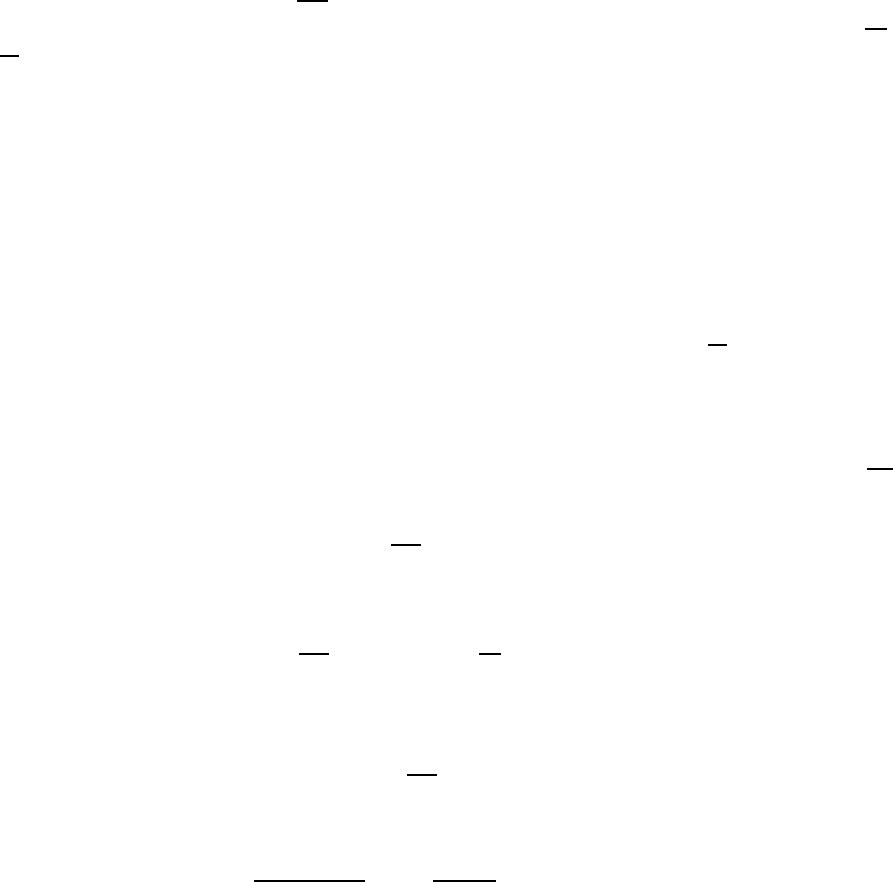
Пусть кодовые слова имеют длину n. Тогда ша р радиуса 1 содержит n + 1 точку. Пусть M = |C|. Тогда

получаем оценку M(n + 1) 6 2

, откуда M 6

n+1

Пусть 2

m−1

6 n < 2

. Тогда 2

6 2n, и, как мы знаем, код Хемминга имеет мощность M = 2

n−m

Отсюда M >

Рассмотрим слу чай, когда 2

−1 = n, то есть 2

= n+1. Тогда верхняя и нижняя оценки для числа M просто

совпадают, то есть код является плотным. Это означает, что имеется плотная упаковка M шаров радиуса 1 в

булев куб B

2.2.4. Коды с исправлением нескольких ошибок

Теперь представим себе, что может происходить не одна, а r ошибок, то есть какие-то r разрядов портятся.

Тогда нужно рассматривать шары радиуса r с центрами в кодовых словах, и они тоже не должны пересекаться.

Пусть S

— объём шара радиуса r. Ясно, что

= C

+ C

+ . . . + C

. (20)

Следствие 2.2. Мощность кода, исправ ляющего r ошибок, не превосходит величины

Оценим снизу мощно с ть кода C

, исправляющего r ошибок. Ясно, что если α, β ∈ B

, и ρ(α, β) > 2r + 1, то

шары с центрами в точках α и β не пересекаются. Поэтому эти слова можно взять в качестве кодовых. Тогда

рассмотрим (тупой) алгоритм построения кода: берём произвольную точку в B

, объя вляем её кодовым словом

и описываем вокруг неё шар радиуса 2r. Точки этого шара уже брать нельзя, а все остальные — можно. Находим

точку в кубе, которая не попала в этот шар и повторяем процедуру. Ясно, что так заведомо можно сделать

раз, поэтому нам гарантирована мощност ь кода

M >

. (21)

Имеется очевидная асимптотика S

∼ n

при n → ∞, поэтому получаем оценки, верные для всех достаточно

больших n при фиксированном r:

6 M

(n) 6 C

. (22)

Пусть мы хотим передавать сообщения из t-битных слов. Тогда нам нужен код мощности M

> 2

. Отсюда

(и из оценки выше) получаем асимптотическое неравенство

6 C

. (23)

Положим n := t + 2r log

t + C, где C = const. Тогда неравенст во перепишется в виде:

1 6 C

t+2r log

t+C

· 2

= C

· 2

∼ C

· 2

. (24)

Отсюда ясно, как подбирать константу C. Это ну жно делать так, чтоб ы асимпто тически неравенство было

выполнено.

Таким образом, мы видим, что «прирост» количества контрольных разрядов сравнительно мал, а именно,

линейно растёт по r и логарифмически — по t.

2.2.5. Линейные коды

При рассмотрении линейных кодов мы будем рассматривать в качестве выходного и выходно го алфавито в

поле F

, где q — простое число. Это поле обозначим для краткости буквой K.

Зафиксируе м натуральные числа n и k < n. Рассмотрим линейный оператор H : K

→ K

n−k

. Матрицу этого

оператора будем называть прове рочной.

Определение. Линейным кодом V с проверочной матрицей H называется ядро оператора H, то есть

V := {x ∈ K

: Hx = 0}. (25)

Как мы знаем, ядро линейного оператора является линейным подпространством. Поскольку dim Ker H +

+ dim Im H = dim K

= n, получае м, что dim V > k.

Мы будем использовать ра сстояние Хемминга, а под нормой вектора, соотве тственно, понимать количество

ненулевых координат в нём.

Число n называется длиной кода V , число k(V ) := dim V — размернос тью кода, а через d(V ) будем обозначать

минимальное расстояние между элементами кода, то есть

d(V ) := min

x,y∈V

x6=0

ρ(x, y) = min

x∈V

x6=0

kxk. (26)

Такой код мы будем называть [n, k, d]-кодо м.

Замечание. Вообще говоря, не следует путать числа k и k(V ). Однако, если нам повезло, и о ператор H

имеет полный ранг (то есть n −k), то k = k(V ), и его матрицу можно привести к виду H = (A|I

n−k

), где I

n−k

—

единичная матрица.

Заметим, что если минимальное расстояние кода равно d, то он умеет исправлять t :=



d−1



ошибок, потому

что шары радиуса t с центрами в кодовых слов ах не пересекаются.

Рассмотрим матрицу G = (I

|−A

), тогда простая проверка показывает, что HG

= 0. Это тем более видно

из того, что G



−A



Определение. Матрица G называется порождающей матрицей кода V .

Суть порождающей матрицы проста: Im G = Ker H = V .

Схема кодирования устроена следующим образ ом:

u = (u

, . . . , u

)

код

−−→ x = (x

, . . . , x

)

помехи

−−−−→ y = (y

, . . . , y

)

декод

−−−−→ eu = (eu

, . . . , eu

). (27)

Из-за возможных помех в канале связи, вообще говоря, x 6= y. Кодирование происходит по схеме x = G

Проверка того, произошли ли ошибки, проводится с помощью матрицы H, применяемой к полученному из

канала связи вектору y.

Теорема 2.10. Пусть H — проверочная матрица кода V . Минимальное расстояние d(V ) кода V равно d

тогда и только тогда, когда любые d −1 столбцов матрицы H линейно независимы, и существует d линейно

зависимых столбцов.

 Пусть d(V ) = d. Тогда существует x ∈ V , такой что kxk = d. Пусть в векторе x ненулевые числа стоят

на местах i

, . . . , i

. Пусть матрица H состоит из столбцов h

, . . . , h

. Поскольку Hx = 0, получаем, что

+ . . . + x

= 0. (2 8)

Это есть искомая нулевая линейная комбинация для столбцов h

, . . . , h

, значит, они линейно зависимы. Теперь,

если бы наш лись d − 1 линейно зависимых столбцов, то коэффициенты линейно зависимости образовали бы

вектор вес а d − 1, за нуляющийся матрицей H, что невозможно. Все наш и рассуждения обратимы, поэ тому

обратное тоже верно. 

Следствие 2.3. Если в проверочной матрице любые d − 1 столбцов линейно независимы, то d(V ) > d.

Следствие 2.4 (Граница Синглтона). Имеет место неравенство d(V ) 6 n − k + 1.

 Так как максимальное число линейно независимых ст олбцов равно рангу матрицы H, а ранг матрицы H

никак не больше n − k, поэтому d(V ) − 1 6 rk H 6 n − k. О тсюда сразу получаем доказываемое неравенство. 

Определение. Синдром — эт о вектор S := Hy.

Если представить y в виде y = x+ e, где e — вектор ошибо к, то полу чаем Hy = Hx+He = He, поскольку x ∈

∈ V = Ker H. Таким образом, ненулев ы е элементы синдрома — это в точности те разряды, в которых произошли

ошибки.

2.2.6. Код Хемминга как пример линейного кода

Теперь, наконец, можно дать определение кода Хемминга в тер минах линейных кодов.

Определение. Пусть H ес ть матрица над полем F

, в которо й r строк и 2

−1 столбцов, причём её столбцы —

все различные ненулевые векто ра из F

. Линейный код, для которого эта матрица является проверочной, и есть

двоичный код Хемминга.

Стоит объяснить, по чему та схема кодирования, которую мы описали вначале, задаёт именно этот код. Это

становится ясно, если заметить, что столбцы в матрице H можно расставить таким образом, чтобы номера

столбцов, в которых ст оят единицы на i-й строке, были элементами последовательности V

i−1

. Это означает, что

вектор Hx состоит из всех сумм вида

k∈V

i−1

(29)

и равен нулю тогда и только тогда, когда все эти суммы равны нулю.

Утверждение 2.11. Код Хемминга есть двоичный [n, k, d]-код, где n = 2

− 1, k = 2

− 1 − r, d = 3.

 В доказательстве нуждается лишь тот факт, что этот код имеет минимальное расстояние 3. П окажем,

что он не содержит векторов, вес которых меньше 3. Предположим противное. Пусть, например, в нём нашелся

вектор x, содержащий только одну единицу в разряде с номером i. Тогда из равенст ва Hx = 0 следует, что i-й

столбец матрицы H должен быть нулевым, а это противоречит о пределению. Аналог ично, если единиц ровно

две — на i-м и j-м местах, то равенство Hx = 0 означает, что сумма i-го и j-го столбцов матрицы H равна нулю,

то есть они попросту совпадают. Опять противоречие, которое и доказывает наше утверждение. 

Из общих свойст в корректирующих кодов следует, что линейный код V , исправляющий t ошибок, имеет

минимальное расстояние не меньше 2t + 1.

2.3. Коды БЧХ

Здесь мы тоже будем говорить о корректирующих линейных кодах и изучим более эффективные алгоритмы

их построения.

2.3.1. Эффективное построение корректирующих кодов

Здесь мы будем рассматривать двоичные коды, то есть K = F

Сначала приведём (тупой) алгоритм построения проверочной матрицы линейного кода с минимальным рас-

стоянием не меньше заданного числа d. Берём матрицу H (первоначально пустую) из r строк и n столбцов.

Пусть её столбцы — h

, . . . , h

. В качест ве h

берём любой ненулевой вектор. Дальше действуем по индукции:

пусть мы уже знае м столбцы h

, . . . , h

, с реди которых любые d − 1 линейно независимы. Тогда покажем, что

выполняется неравенство N := C

+ C

+ . . . + C

d−2

< 2

−1. Что значит, что вектор h

i+1

можно добавить к уже

имеющимся так, чтобы сохранилось условие линейной независимости любых d − 1 ве кторов? Это з начит, что

линейная оболочка любых d − 2 векторов не должна исчерпывать всё пространство K

(без нуля). Очевидно,

мощность линейной оболочки не больше количества всевозможных линейных комбинаций, а их всего ровно N

штук. Значит, при N < 2

− 1 заведомо (i + 1)-й вектор добавить можно.

Следствие 2.5 (Граница Варшамова – Гилберта). Если C

n−1

+ C

n−1

+ C

n−1

+ . . . + C

d−2

n−1

< 2

, то

существует матрица n × r, у которой любые d − 1 столбцов линейно независимы.

 Очевидным образом с ледует из алгоритма: если нерав е нство ещё не обрат илось в равенство при n − 1

столбце, то найдётся место и для n-го. 

2.3.2. Построение поля из 2

элементов

Поле Галуа F := GF (2

) из 2

элементов строится как факторкольцо кольца многочленов F

[x] по идеалу,

порождённому неприводимым многочленом степени m. Это поле является m-мерным ве кторным пространством

над полем F

. Иногда мы будем рассматривать его элементы как многочлены с тепени мень ше m над полем F

а иногда — как наборы их коэффициентов, то есть m-мерные вект ора из нулей и единиц.

Напомним, что в поле характеристики p имеет место автоморфизм Фробениуса (a + b)

= a

+ b

, так как

все остальные биномиальные коэффициенты делятся на p и потому в этом поле равны нулю. Применяя эту

формулу несколько раз, получаем более общий факт: (a + b)

= a

+ b

, и очевидно, что она верна и для

нескольких слагаемых.

2.3.3. Двоичные коды БЧХ

Пусть n = 2

− 1, и α

, . . . , α

— все ненулевые элементы поля F . Через γ

будем обозначать столбец

коэффициент ов многочлена α

(то есть α

и γ

— это разные записи одного и того же объекта).

Рассмотрим матрицы

A :=







. . . α

··· ··· ··· ···

2t−1

. . . α

2t−1







t×n

H :=







. . . γ

··· ··· ··· ···

2t−1

. . . γ

2t−1







tm×n

(30)

Определение. Кодом БЧХ (Боулз – Ч оудхури – Хоквингем) называется код с проверочной матрицей H.

Теорема 2.12. В м а т рице H любые 2t столбцов ли нейно независ имы.

 Допустим, что это не так, и нашлись линейно зависимые столбцы h

, . . . , h

, где l 6 2t. Тогда имеем

:= α

+ . . . + α

= 0,

:= α

+ . . . + α

= 0,

···

2t−1

:= α

2t−1

+ . . . + α

2t−1

= 0.

(31)

Покажем, что степенные суммы S

с чётными но мерами тоже равны нулю. Пусть k = 2

u, где u нечётно. Тогда

в силу автоморфизма Фробениуса (S

)

= S

. Значит, если S

= 0, то и S

= 0.

Таким образом, получа ем, что S

= 0 при i = 1, . . . , l. Это «кусочек» матрицы Вандермонда, столбцы которой

линейно независимы, если все элементы α

различны (а в нашем случае это именно так). Противоречие. 

Тут ещё был очень малопонятный пример... для случая двух ошибок.

2.4. Алгоритм Питерсона

2.4.1. Теория

Здесь все рассуждения проводятся для произвольного поля F из q

элементов.

Определение. Пусть b — целое неотрицательное число, и пусть α ∈ F — примитив ный корень n-й степени

из 1 , где m является мультипликативным порядком числа q по модулю n. Тогда кодом БЧХ длины n с кон-

структивным расстоянием d, где 2 6 d 6 n, над полем F называется циклический код, определяемый корнями

, α

b+1

, . . . , α

b+d−2

порождающего многочлена g(x).

Порождающая матрица кода с порождающим многочленом g(x), deg g(x) = n − k, имеет вид

G =







. . . g

n−k

0 0 . . . 0

0 g

. . . g

n−k

0 . . . 0

. . .

0 0 . . . 0 g

. . . g

n−k







. (32)

Замечание. До сих пор мы рассматривали случай b = 1 (БЧХ-код в узком смысле), n = q

−1 (примитивный

БЧХ-код) и, наконец, q = 2.

Обозначим через w(x), v(x) и e(x) передаваемый кодовый многочлен, принимаемый мно г очлен и многочлен

ошибок соответственно; т огда v(x) = w(x) + e(x). Прежде всего найдем синдром вектора v:

S(v) = Hv

= (S

, S

b+1

, . . . , S

b+d−2

)

, (33)

где

= v(α

) = w(α

) + e(α

) = e(α

), b 6 j 6 b + d − 2. (34)

Если имеется r 6 t ошибок, то

e(x) =

i=1

, (35)

где a

, . . . , a

— различные элементы из {0, . . . , n − 1}. Элементы η

= α

∈ F называются локаторами ошибки,

а элементы c

∈ Z

∗

— значениями ошибки. Таким образом, для синдрома получаем формулу

= e(α

) =

i=1

, b 6 j 6 b + d − 2, (36)

а тогда

i=1

= S

. (37)

В двоичном случае последняя формула — это формула для вычисления четных элементов синдрома.

Нам надо найти неизве с тные пары (η

, c

). В двоичном с лу чае все c

могут принимать лишь значение,

равное 1, поэтому искать их не нужно.

Следующим шагом декодирующего алгоритма является нахожде ние коэффициентов σ

, задаваемых так:

i=1

(η

− x) =

i=0

(−1)

r−i

. (38)

Таким об разом, σ

= 1, а σ

, . . . , σ

— элементарные симметрические мног очлены от η

, . . . , η

. Подставляя

вместо x, получаем для всех i = 1, . . . , r:

(−1)

+ (−1)

r−1

+ . . . + (−1)σ

r−1

+ η

= 0. (39)

Умножим на c

и просуммируем по всем i:

(−1)

+ (−1)

r−1

j+1

+ . . . + (−1)σ

j+r−1

+ S

j+r

= 0, (40)

где j = b, b + 1, . . . , b + r − 1.

Лемма 2.13. Система уравнений

i=1

= S

, j = b, b + 1, . . . , b + r − 1, (41)

относительно неизвестных c

разрешима , если η

различны.

 Определитель этой системы есть определитель Вандермонда, умноженный на η

· . . . · η

. 

Лемма 2.14. Система уравнений

(−1)

+ (−1)

r−1

j+1

+ . . . + (−1)σ

j+r−1

+ S

j+r

= 0, (42)

где j = b, b + 1, . . . , b + r −1 относительно неизвестных (−1)

однозначно разрешима тогда и только тогда,

когда в полученном слове имеется ровно r ошибок.

 Матрица этой системы равна V DV

, где V — определите ль Вандермонда от переменных η

степени

r − 1, а D — диагональная матрица с элементами вида c

на главной диагонали. Она нев ы рождена т огда и

только тогда, когда невырождены V и D — то есть как раз когда имеется ровно r различных ошибо к. 

2.4.2. Практика

Теперь, наконец, можно перейти к самому алгоритму Питерсона. Итак:

◦

Находим синдром полученного слова

S(v) = Hv

= (S

, S

b+1

, . . . , S

b+d−2

)

⊤

. (43)

Пусть

i=1

, b 6 j 6 b + d − 2. (44)

◦

Находим максимальное число r 6 t, такое, что сист ема уравнений

(−1)

+ (−1)

r−1

j+1

+ . . . + (−1)σ

j+r−1

+ S

j+r

= 0, (45)

где j = b, b + 1, . . . , b + r −1 относительно неизвестных (−1)

имеет невырожденную матрицу коэффи-

циентов. Тем самым получаем число появившихся ош ибок. Построим многочлен локаторов ошибки:

s(x) =

i=1

(1 − η

x) =

i=0

. (46)

Коэффициент ы σ

выражаем через S

◦

Решаем уравнение s(x) = 0 и находим локаторы ошиб ки η

. В двоичном случае на э том всё заканчивается.

◦

Подставляя η

в систему

i=1

, b 6 j 6 b + d − 2, (47)

полученную на 1-м шаге, находим значения ошибки c

3. Схемы из функциональных элементов

При раб оте с булевыми функциями мы иногда будем заменять значок & обычной точкой (произведением)

или не писать его вовсе.

3.1. Схемы из функциональных элементов

Определение. Схема из функциональных элементов (СФЭ) — это конечный ориентированный граф бе з

ориентированных циклов, в каждую вершину которого входит н е более 2 рёбер. При этом каждой вершине при-

писывается символ: переменная x

, если в эту вершину рёбра не входят; отрицание, если в вершину входит одно

ребро; конъюнкция или дизъюнкция, если в вершину входит 2 ребра. Некоторым вершинам приписывается ∗.

Элементами схемы называются вершины, помеченные логическими о перациями.

Занумеруем вершины графа согласно теореме 1.16. К аждой вершине СФЭ можно сопоставить некоторую

булеву функцию по следующему индуктивному правилу. Пусть всем вершинам с номерами меньше n уже со -

поставлены функции. Возьмём ве ршину с номером n. Если в неё не входит ни одного ребра, то ей приписана

переменная, которую мы как функцию и поставим ей в соответствие. Если в вершину входит одно ребро, то

в ней записано отрицание, и мы припишем этой вершине о трицание функции той вершины, из которой в дан-

ную вершину приходит ребро . Если входит два ребра, то в этой вершине будет конъюнкция или дизъюнкция

функций тех вершин, из которых приходят эти рёбра. Видно, что такое определение корректно.

Определение. Функции, отвечающие вершинам, отмеченным ∗, называют ся реали зуемыми данной СФЭ.

6 ∗

∨

Рис. 9. Пример СФЭ

Пример 1.1. Приведённая на рис. 9 схема реализует функцию (x

∨ x

) & (x

& x

) = x

⊕ x

Существует ф изическая интерпретация СФЭ, в которой они рас с матриваются как математические модели

соотв е тствующих реальных элект ронных схем: если на вход подаётся набор значений (наличие тока соответ-

ствует единице, отсутствие — нулю), то на выходе получается значение функции на этом наборе.

Определение. Сл ожностью схемы S называется число элементов L(S) в ней. Сложностью функции f

называет ся минимальная сложность схемы для f. Функция Шеннона L(n) выражает максимальную сложность

функций от n переменных.

Построим СФЭ, реализующую функцию f = x

· . . . · x

. Перегруппируем множители, собрав в одном

месте переменные с нулевыми степенями. Тогда, перенумеровав переменные и применив правило де Моргана,

функцию можно переписать в виде

f = (x

& . . . & x

) & (x

k+1

∨x

k+2

∨ . . . ∨ x

). (1)

Заметим, что в этой формуле не более n операций. Значит, сложность схемы данной функции не превосходит n.

Постройка схемы по данной формуле предоставляется читателю.

Утверждение 3.1.

L(n) 6 (n + 1) · 2

. (2)

 Рассмотрим произво льную функцию f от n переменных и построим её СДНФ. В ней может быть не

более 2

дизъюнкций выражений вида x

· . . . · x

. Так как сложность каждого дизъюнкта мы уже оценили

числом n, то сложность все й схемы не превосходит n · 2

+ (2

− 1) < (n + 1) · 2

. Для функций, тождественно

равных нулю, можно использова ть формулу f = x

& x

. При этом мы предполагаем, что f — функция по

крайней мере от одной переменной. Схема будет содержать 2 элемента, значит, её сложность L(f ) = 2 6 n · 2

Итак, сложность любой функции L(n) 6 (n + 1) · 2

. 

Замечание. На самом деле легко доказать, что L(n) 6 (n + 1) ·2

n−1

. Действительно, посмотрим на таблицу

значений нашей функции и выясним, чего в ней больше: нулей или е диниц. В зависимости от этого будем исполь-

зоват ь, соотв е тственно, СДНФ либо СКНФ. В самом худшем случае будет 2

n−1

дизъюнкций или коньюнкций.

Следствие 3.1. В силу сделанного замечания верна оценка L(n) 6 n · 2

, так как

· (n + 1) · 2

6 n · 2

Обозначим через K

множество всех функций вида x

· . . . · x

. Сейчас мы будем строить схему, которая

реализует все функции из K

. Сложность тако й схемы обо з начим C(n).

Мы будем делать это индуктивно. При n = 1 делать почти нечего. Предположим, что мы уже построили

схему для всех множеств с номерами меньше n. Заф иксируем число k < n. Построим схему, реализующую все

функции из K

, используя в качестве подсхем две схемы: для K

и для K

n−k

Рассмотрим произвольную конъюнкцию

· . . . · x

= (x

· . . . · x

) & (x

k+1

· . . . · x

). (3)

Возьмём по одному выходу из схем для K

и K

n−k

, реализующие множители в скобках, и подключим их к

конъюнктору. Получим схему, реализующую одну конъюнкцию n переменных. Также поступим со всеми 2

конъюнкциями n переменных, то есть будем делать их, используя соответствующие выходы в схемах K

n−k

, связывая их конъюнкторо м. Итого получим схему для K

, затратив C(k) + C(n − k) + 2

элементов.

Теперь возьмём k :=

. Значит,

C(n) 6 2

+ 2C





= 2

+ 2



+ 2C





= 2

+ 2





= ··· . 2

. (4)

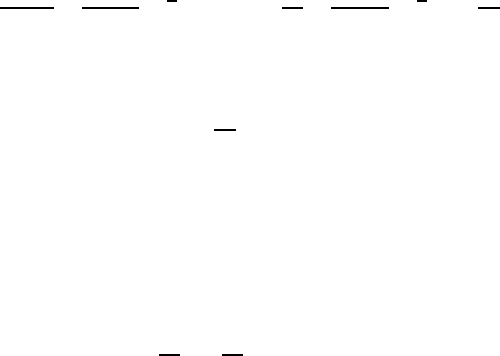
Отсюда следует, что можно (асимптотически) улучшить оценку для L(n): реализовав все конъюнкции ценой

∼ 2

элементов, склеим их не более чем 2

дизъюнкциями, в итоге получим схему сложности порядка 2

n+1

3.1.1. Метод Шеннона синтеза схем

Все дальнейшие оценки будут ас имптотическими, по э тому мы не будем всякий раз об этом упоминать . Так

как никаких других логарифмов в дискретной математике не встречается, под log мы всегда будем понимать

log

Мы будем использовать разложение функции по переменным:

f(x

, . . . , x

) =

(σ

,...,σ

)

· . . . · x

f(σ

, . . . , σ

, x

q+1

, . . . , x

). (5)

Пусть q = n − k. Реализуем все конъюнкции K

первых q переменных, при этом потрат им 2

элементов. Кроме

этого, нам по максимуму может потребоваться реализовать все функции от k переменных, коих имеется 2

штук. Не напрягаясь, реализуем каждую из них со сложностью k ·2

. При склейке основной схемы по указанной

выше формуле потребуется ещё 2

конъюнкторов (для вычисления слагаемых) и ещё 2

−1 дизъюнкторов. Ит ого

L(f) . 2

+ 2

+ (2

− 1) + k · 2

· 2

. 3 · 2

+ k · 2

· 2

. (6)

Выбор k — дело ответственное. Нам нужно, чтобы последнее слагаемое не было очень большим. Логично взять

k = log n, но, если подставить , получается многоват о. Поэтому возьмём k := [log n] − 1. Тогда

L(f) . 3 · 2 ·

[log n]

n log n

· 2

. 3 · 2 · 2 ·

n log n

· 2

. 12

. (7)

3.1.2. Асимптотически наилучший метод построения схем

Теорема 3.2 (О. Б. Лупанов).

L(n) .

. (8)

 Рассмотрим произвольную булеву функцию n переменных. Отделим q := n − k первых переменных и

рассмотрим таблицу, в которой 2

строк и 2

столбцов. Строки занумеруем всевозможными значениями послед-

них k переменных, а столбцы — всевозможными значениями первых q переменных. Ячейки таблицы заполним

значениями функции. Ка ждый столбец представляет собой з начения функции, полученной подстановкой кон-

стант в первые q переменных, то есть f(σ

, . . . , σ

, x

q+1

, . . . , x

). Разрежем таблицу на горизонтальные полоски

по s строк в каждой (последняя по лоса будет, возможно, меньше; пусть в ней s

′

< s строк). Число полос будет

равно

p :=





+ 1. (9)

Через I

обозначим индикатор i-й полосы, то есть функцию, которая равна единице на строках этой по лосы,

и только на них. Обозначим теперь f

(σ

,...,σ

),i

q+1

, . . . , x

) := f (σ

, . . . , σ

, x

q+1

, . . . , x

) · I

. Такие функции

будем называ ть обрезанными функциями. Ясно, что

f(σ

, . . . , σ

, x

q+1

, . . . , x

) =

i=1

(σ

,...,σ

),i

q+1

, . . . , x

). (10)

Имеем

f(x

, . . . , x

) =

(σ

,...,σ

)

· . . . · x

· f(σ

, . . . , σ

, x

q+1

, . . . , x

). (11)

Реализуем все конъюнкции первых q переменных, потратив 2

элементов. Кроме это г о, реализуем все конъюнк-

ции последних k переменных, потратив 2

элементов. Все обрезанные фу нкции имеют не более s ненулевых

значений, значит, их количество не превышает 2

. Поскольку все конъюнкции последних переменных уже есть,

на изготовление СДН Ф для каждой обрезанной функции уйдёт всего s дизъюнкций, з начит, всего на реализа цию

обрезанных функций каждой полосы мы потра тим не более s · 2

элементов, а всего — не более p · s · 2

На сборку каждой f(σ

, . . . , σ

, x

q+1

, . . . , x

) уйдёт ещё p дизъюнкций (поэтому всего на это уйдёт p · 2

операций), а на сборку функции f уйдёт ещё 2

конъюнкций и 2

дизъюнкций.

Суммируя полученные оценки, имеем

L(f) . 2

+ 2

+ ps · 2

+ p · 2

+ 2

= 3 · 2

+ ps · 2

+ p · 2

+ 2

. (12)

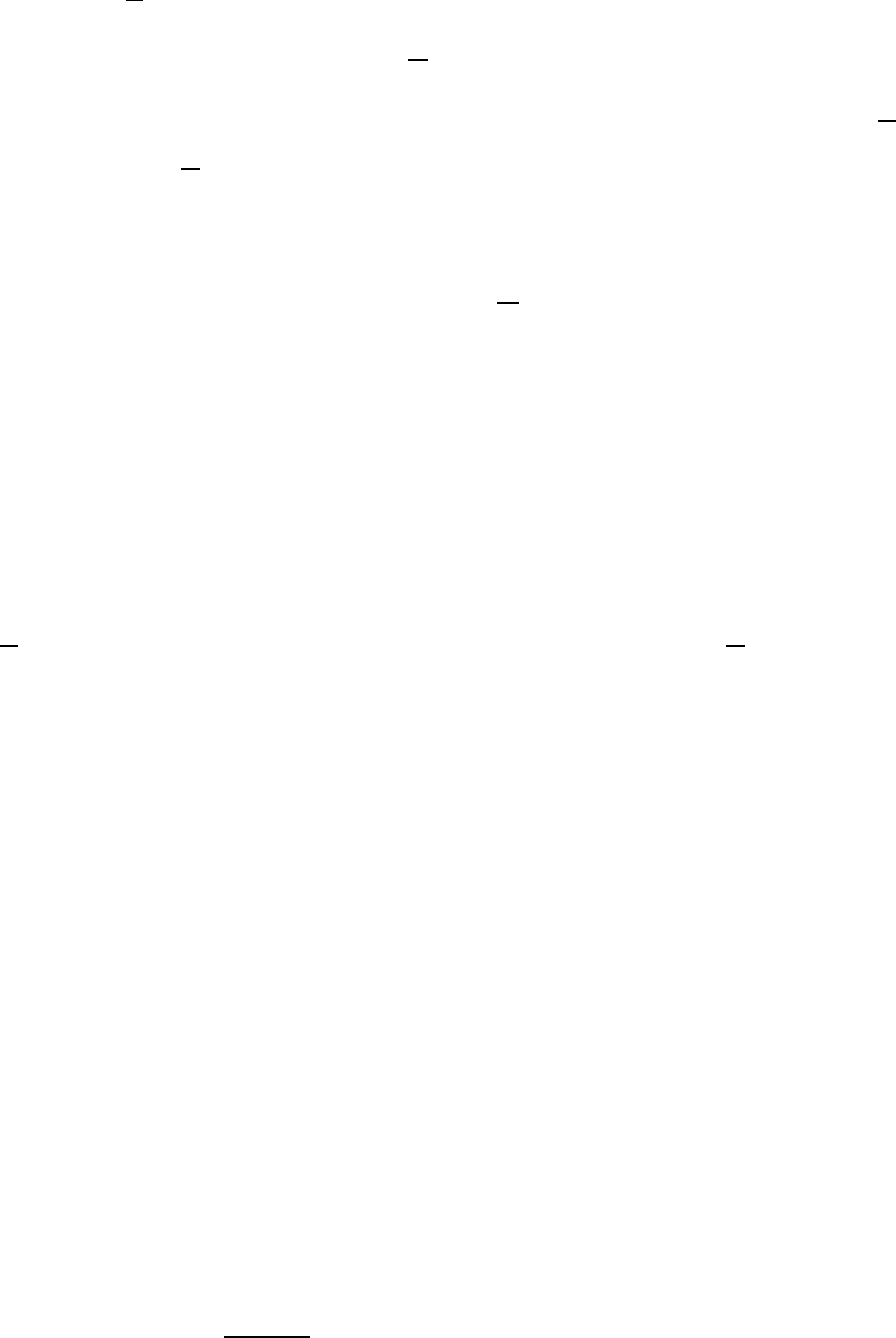
Вспоминая, что p <

+ 1, получаем

L(f) . 3 · 2



+ 1



(s · 2

+ ·2

) + 2

. (13)

Видно, что s должно быть порядка n, но всё же чуть меньше его. Что касается k, то ну жно, чтобы

→ ∞,

чтобы нам не мешала единица в скобках. Положим k := [2 log n] и s := [n − 4 log n]. Подставляя эти значения,

получаем оценку порядка

(выкладки временно предоставляем читателю). 

3.1.3. Асимптотическая оценка снизу для сложности схем

Теорема 3.3. Для любого ε > 0 выполено асимптотическое неравенство

L(n) & (1 − ε)

. (14)

 Введем с леду ющие обозначения:

• P

∗

(n) — функции, существенно зависящие от n переменных.

• N(h, n) — число функций, существенно зависящих от n переменных, которые реализуются схемами слож-

ности, не превосходящей h.

• N

′

(h, n) — число функций, существенно зависящих от n переменных, которые реализу ются схемами слож-

ности ровно h;

• N

′′

(h, n) — число схем сложности h для функций, существенно зависящих от n переменных;

Очевидно, что N

′

= N, потому что всегда можно дополнит ь схему ничего не дела ющими элементами. Оче-

видно также, что N 6 N

′′

, так как одну функцию можно реализовать разными схемами, но не наоборот.

Идея доказательства состоит в том, чтобы показать, что ф ункций, реализуемых схемами с ложностью меньше

(1 − ε)

, гораздо меньше, чем всех функций. Итак, покажем, что для h

:= (1 − ε)

выполнено N(h

, n) <

< |P

∗

(n)|. Мы будем оценивать величину N, мажорируя её величиной N

′′

Пусть γ(p, q) — число графо в с q ребрами и p := h + n ве ршинами (n в ходов и h элементов), N

′′

(h, n, q) —

число схем с q ребрами. Сколько схем можно сделать из одного графа? У нас имеется не более:

• 2

способо в выбрать ориентацию ребер;

• (h + n)

способо в выбрать входы;

• 3

способо в присвоения вершинам различных ФЭ;

• h + n способов вы бора выхода.

Итак, вспоминая оценку для числа графов, получаем:

′′

(h, n, q) 6 γ(p, q) · 2

· (h + n)

n+1

· 3

6 A

h+n+q

(h + n)

q−h+1

· 2

· 3

. (15)

Вспоминая, что q 6 2h, и собирая константы, окончатель но запишем:

′′

(h, n, q) 6 B

3h+n

(h + n)

h+1

. (16)

Теперь получим оценку для N

′′

(n, h):

′′

(n, h) 6

q=h

′′

(h, n, q) 6 B

3h+n

(h + n)

h+1

(h + 1) 6 (C(h + n))

h+n

. (17)

Нам нужно убедиться, что N

′′

, n) < |P

∗

(n)| при достаточно больших n. Заметим, что

∗

(n)| > 2

− n2

n−1

∼ 2

. (18)

Таким образом, требуемое неравенство будет выполнено, если

log

′′

, n)

∗

(n)|

= log N

′′

, n) − 2

+ o(1) → −∞, n → ∞. (19 )