Луизов А.В. Цвет и свет
Подождите немного. Документ загружается.

τ = Ф/Ф
0
. (14.5)
Рассеяние значительно усложняет приведенные нами зависимости. Поэтому
применяются меры, чтобы в материалах, используемых в фотометрии (например, в
светофильтрах), рассеяния практически не было. Впрочем, иногда его, наоборот,
используют, например, в молочных стеклах. Идеальное молочное стекло должно, не
поглощая света, рассеивать его так, чтобы вошедший в него свет полностью терял
первоначальное свое направление и выходил, почти равномерно распределенный по всем
направлениям.
Конечно все величины, о которых мы сейчас говорим, зависят от спектрального состава
света и в колориметрии их приходится определять как функции длины волны (Ф
0λ
; Ф
λ
; r(λ);
k(λ)). В особенности важен спектральный коэффициент пропускания τ(λ) – основная
характеристика светофильтров.
14.8. Спектрофотометр.
Поскольку измерения спектрального апертурного коэффициента отражения обычно
ограничивают одним из стандартных вариантов, спектрогониофотометры применяются
редко. Широкое распространение получили приборы, работающие в соответствии с каким-
нибудь одним вариантом. Поскольку в них уже никакие углы не меняются, их нельзя назвать
спектрогониофотометрами. Их называют проще – спектрофотометрами.
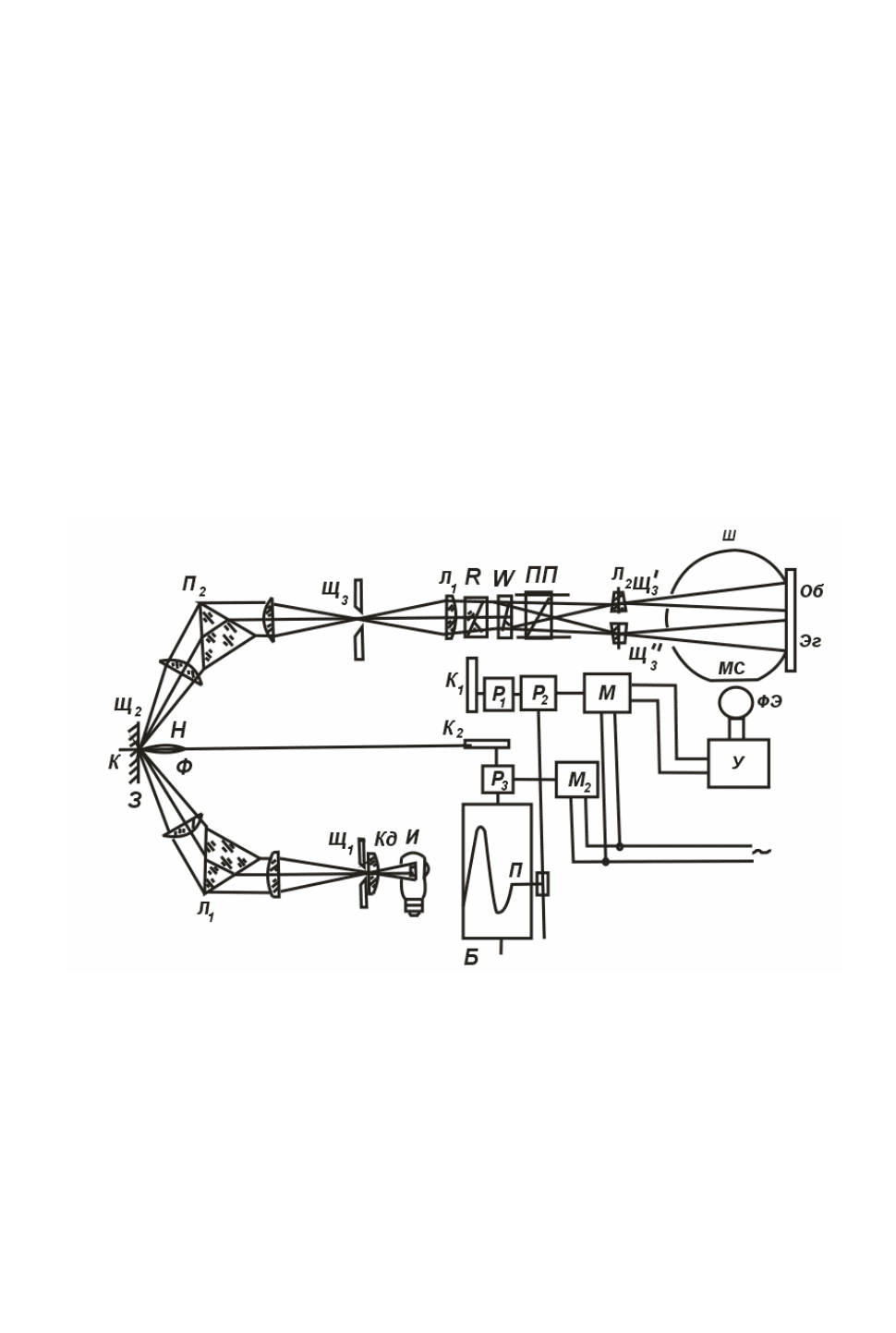
Рис.
14.5. Схема спекрофотометра.
На рис. 14.5 изображена схема выпускаемого в Советском Союзе спектрофотометра
СФ-18. В приборе осуществлен стандартный вариант измерения О/Д. Источником света И
служит кннопроекционная лампа К17 (17 В, 170 Вт). Через конденсор Кд ,и щель Щ
1
ее свет
входит в двойной монохроматор П
1
–П
2
и выходит из него через щель Щ
3
. Промежуточная
щель Щ
2
, выделяющая ту или иную часть спектра, образована зеркалом 3 и ножом Н. Для
перехода от одной длины волны к другой нож перемещается вдоль зеркала перпендикулярно
своей плоскости. Расстояние его до зеркала остается постоянным, и второй половиной щели
служит отражение ножа. Выходящий из монохроматора пучок через линзу Л
1
призму Рошона
R, призму Волластона W , а также призмы ПП, попадает на две половины линзы Л
2
и, пройдя
через две щели Щ’
3
и Щ’’
3
, идет, в виде двух пучков в интегрирующий шар Ш, В
противоположной стенке шара сделаны два отверстия, к которым можно прижать
исследуемый объект (Об) и совершенный отражающий рассеиватель (Эт). Призма Рошона

Подставив сюда конкретные значения координат цвета, находим L(Ц) = 19,38К
я
.
Полученное значение яркости легко проверить, поскольку в нашем примере известна
энергетическая яркость L
е
= 60·Вт·м
-2
·ср
-1
и длина волны λ = 500 нм. Соотношение между
яркостью L и энергетической яркостью L
е
имеет вид L = К
m
L
e
V(λ).
По табл. 3.1 находим V(500) = 0,323, откуда L = К·60·0,323 = 19,38 К
я
, т. е. то же, что
мы получили по формуле (15.2). Совпадение результатов, конечно, неслучайно. Оно
оправдывает рациональ ность выбора в качестве коэффициента К в формуле (15.2) значения
К
m
.
Следовательно, для единичных цветов можно принять: L(R) = K
я
; L(G) = 4,5907·К
я
;
L(В) = 0,0601·К
я
15.3. Яркость цвета в системе XYZ.
Вычислим яркости единичных цветов в системе ХУZ. Достаточно найти их яркостные
коэффициенты, а яркость получится умножением на Кm
Возьмем цвет Ц
б
с координатами r' = g' = b' = 1. Равенство координат показывает, что
это белый равноэнергетический цвет, яркость которого
L(Ц
б
) = К
я
(1 + 4,5907 + 0,0601) = 5,6508K
я
.
В системе ХУZ цвет Ц
б
должен быть тоже белым равноэнергетическим (вспомним, что
базисный стимул у обоих один и тот же), что соответствует условию х' = у' = r'. Яркость
цвета Ц тоже должна остаться прежней. Вычислим координаты Ц в системе ХУZ. Подставив
в формулы (8.21) значения r' = g'= b' =1, получим х' = 5,6508; у' = 5,6508; z' = 5,6508.
Поскольку яркостные коэффициенты L
x
= L
z
= 0, вся яркость цвета Цб, т. е. 5,6508 K
я
,
определяется координатой у' = 5,6508. Отсюда легко найти яркость единичного цвета.
Таким образом подтверждается, что, выбрав не-которое значение коэффициента К в
формуле (8.35), мы можем сохранять его неизменным при переходе от системы RGB к
системе ХУZ и обратно.
Подставим в формулах (8.22) вместо Р
λ
спектральную плотность энергетической
яркости получим
∫
∫
∫
=
′
=
′
=
′
λλλλλλ
λλλ
dzLzdyLydxLx
eee
)( ;)( ;)(
. (15.3)
Получив по этим формулам координаты *', у' и г' цвета Ц, найдем его яркость
L(Ц) = L(Y)
y
= K
Я
y
. (15.4)
15.4. Переход от любой системы в систему XYZ.
В визуальных колориметрах обычно применяются три основных цвета: красный К,
зеленый 3 и синий С. Основными цветами колориметра не могут быть цвета X, Y и Z, так
как они реально неосуществимы. Цвета R, G и В могут быть осуществлены, но применяются
очень редко. Чаще всего берут какие-то произвольные цвета с довольно большой (но не
равной единице) частотой, а по цветовому тону расположенные в красной, зеленой и синей
области спектра. Поэтому измерения, проведенные на колориметре, как правило, требуют
пересчета, обычно в господствующую сейчас систему ХУZ.
Как проводить такой пересчет, покажем на при-мере колориметра Демкиной
(см. рис. 10.1). Количество каждого из основных цветов в цвете измеряемого образца Ц
пропорционально углам α' (для красного), β' (для зеленого) и γ′ (для синего) раскрытия
заслонок в диафрагмах Д. Введем величины α, β и γ. характеризующие относительное
открытие каждой заслонки:
α = α'/α
П
; β = β'/β
П
; γ = γ'/γп (15.5)
где α
п
, β
п
и γ
п
– углы, соответствующие полному раскрытию диафрагм, для излучений К, 3 и
С.
Проще всего проградуировать колориметр, если мы знаем все три основных цвета, т. е.
можем написать:
К = x
к
X + y
к
Y + z
к
Z; З = x
З
X + y
З
Y + z
З
Z; C = x
c
X+y
c
Y+z
c
Z (15.6)

здесь К, 3, С – цвет каждого из основных цветов при полном открытии заслонок.
Теперь, если, измеряя какой-то цвет Ц, мы сдвинули заслонки так, что получили.
величины α, β и γ, координаты цвета Ц определим по формулам
x′ = αx′
К
+ βx′
З
+ γx′
C;
y′ = αy′
К
+ βу′
З
+ γx′
C;
z = αz′
К
+ βz′
З
+ γz′
C
(15.7)
Цвета К, 3, С мы можем либо прямо измерять каким-либо колориметром, либо,
определив спектральную мощность Р
λ
света, доходящего до фото метрического кубика К
через каждый из фильтров К, 3 и С, рассчитать координаты основных цветов по формулам
(8.22).
Если заранее о цветах К, 3 и С ничего неизвестно, градуировку приходится проводить
более сложным способом, например методом трех фильтров. Координаты цвета каждого из
трех фильтров должны быть известны с большой точностью.
В колориметре Демкиной осветитель А с фильтром ДК освещает образец Об светом,
соответствующим стандартному источнику А. В качестве образца установим совершенный
отражающий рассеиватель. В качестве элемента Ф поставим сначала фильтр 1, Зная
спектральный состав источника А, т. е. Р
λ
для него и спектральное пропускание первого
фильтра, мы можем вычислить цвет Ц
1
совершенного отражателя при фильтре 1. Уравняем
этот цвет с цветом, составленным из трех основных цветов колориметра, и найдем отсчеты
α
1
, β
1
, γ
1
при которых получается тот же цвет Ц
1
. Поставим фильтр 2 и получим цвет Ц
2
и
вторую комбинацию открытия заслонок α
2
, β
2
, γ
2
, при третьем фильтре – цвет Ц
3
и
комбинацию αз, βз, γз Приравняем друг другу выражение каждого цвета в двух системах
КЗС и ХУZ. Получим три уравнения:
Ц
1
= α
1
К + β
1
3 + γ
1
C = x
1
′X + y
1
′Y + z
1
′Z
Ц
2
= α
2
К + β
2
3 + γ
2
C = x
2
′X + y
2
′Y + z
2
′Z
Ц
3
= α
3
К + β
3
3 + γ
3
C = x
3
′X + y
3
′Y + z
3
′Z (15.8)
В трех уравнениях (15.8) три неизвестных: К, 3 и С. Напишем решение для К с
помощью определителей:
333
222
111
33333
22222
11111
333
222
111
333
222
111
γβα
γβα
γβα
γβ
γβ
γβ
γβα
γβα
γβα
γβ
γβ
γβ
ZzYyXx
ZzYyXx
ZzYyXx
Ц
Ц
Ц
K
′
+
′
+
′
′
+
′
+
′
′
+
′
+
′
==
. (15.9)
Обозначив знаменатель символом и преобразовав числитель с учетом свойств,
определителей, получим
Δ
′
′
′
+
′
′
′
+
′
′
′
=
333
222
111
333
222
111
333
222
111
γβ
γβ
γβ
γβ
γβ
γβ
γβ
γβ
γβ
z
z
z
Z
y
y
y
Y
x
x
x
X
K
. (15.10)
Не будем выписывать решений для 3 и С. Ограничимся указанием, что в числителе
формулы (15.10) нет α. В формуле для 3 не должно быть β
1,
β
2
, βз. На их место следует
ставить х', у' и r' с индексами 1, 2, 3. В формуле для С не должно быть γ которая тоже
заменяется координатами х', у', z'.
Обозначим деленные на Д коэффициенты в решении для К через а
к
, b
к
, с
к
, в решении
для 3 – через а
3
, b
3
, с
3
, в решении для С – через а
с
, b
с
, с
с
. Из вышесказанного ясно, что,
например,
333
222
111
1
y
y
y
b
c
′
′
′
Δ
=
βα
βα
βα
. (15.11)

где
333
222
111
γβα
γβα
γβα
=Δ
=
Таким образом, решения для К, 3 и С приводятся к виду
К = α
к
X + b
к
Y + c
к
Z; З = α
з
X + b
з
Y + c
з
Z; К = α
к
X + b
к
Y + c
к
Z. (15.12)
Предположим, что для уравнивания полей фотометрического кубика при измерении
неизвестного цвета Ц
н
мы получили углы поворота заслонок в диафрагмах α
н
, β
н
и γ
н
; значит,
в единицах К, 3, С мы получили
Ц
н
= α
н
К + β
н
З + γ
н
С (15.13)
Подставив сюда значения К, 3 и С по формуле (15.12), найдем
Ц
н
= α
н
α
к
Х + α
н
b
к
Y + а
н
с
к
Z + β
н
α
з
Х + β
н
b
з
Y + β
н
c
з
Z + γ
н
α
с
X + γ
н
b
c
Y + γ
н
c
c
Z
Вынося X, Y и Z за скобки и принимая во внимание, что коэффициент при X равен х'
н
–
координате цвета Ц
н
в системе ХУZ и что, с коэффициентами при Y и Z дело обстоит так же,
получаем
X
н
′ = α
н
α
к
+ β
н
α
з
+ γ
к
α
с
y
н
′ = α
н
b
к
+ β
н
b
з
+ γ
к
b
с
z
н
′ = α
н
c
к
+ β
н
c
з
+ γ
к
c
с
(15.14)
Таким образом, от системы К, 3, С данного колориметра мы переходим к
общепринятой системе ХУZ.
Существуют и другие методы градуировки колориметров: см., например, статью Н. Б.
Лобановой (29).
15.5. Вычисление цвета по спектрофотометрическим данным.
Если нам известна спектральная плотность мощ-ности Р
Λ
света, идущего от какого-
нибудь источника, или Рλр(λ) – отраженного света или, наконец, Р
λτ
(λ) – света, прошедшего
сквозь селективно поглощающий слой, координаты цвета в принципе находят по формулам
(8.22), (6.8), (9.9) или (9.10). Но поскольку под знаком интеграла всегда стоят
экспериментально найденные величины, выраженные в виде таблиц или графиков, эти
интегралы, конечно, никогда нельзя взять в квадратурах. Приходится прибегать к
численному интегрированию.
Чаще всего Пользуются методом взвешенных координат: весь спектр от 380 до 760 нм
разбивают на равные промежутки λ и интеграл заменяют суммой. Если, например, нужно
вычислить цвет поверхности, спектральный коэффициент отражения которой р(λ), при
источнике со спектральной плотностыо мощности Р
λ
имеем
∑
Δ=
′
λ
λ
λλλρ
)()( xPkx .
Выражения для у' и z' аналогичны. Нормирующий коэффицтент k вычисляется также с
помощъю суммы:
∑
Δ
=
λ
λ
λλ
)(
100
yP
k
. (15.15)
Чем точней нужно найти координаты цвета, тем меньше должно быть ∆λ. Обычно
берут ∆λ = 10 нм или ∆λ = 5 нм.
Другой метод – метод избранных координат – заключается в том, что спектр разбивают
на неравные промежутки ∆λ. Они должны быть такими, чтобы произведение
λ
λ
λ
Δ
)(xP . (15.16)
по всему спектру было постоянным. Значения Р
λ
и х(λ) нужно брать для λ, соответствующей
длине волны в середине интервала ∆λ. Когда эти интервалы (∆λ) найдены, достаточно
сложить все значения р(λ) для λ, лежащих в середине интервалов ∆λ, и сумму р(λ) умножить
на произведение (15.16) (оно одинаково для всех интервалов). Результат множат еще на

нормирующий множитель типа (15.15). Координаты у' и z' находят аналогичным способом,
но для каждой координаты нужно находить свой интервал ∆λ.
Метод избранных координат удобен, когда цвет многих образцов нужно определять
при одном и том же источнике света. Тогда для всех образцов произведение (15.16)
постоянно. Постоянны такие же, аналогичные (15.16), произведения и для координат у' и z'
(хотя для каждой координаты они различны), постоянен и нормирующий множитель.
Меняется только р(λ) для разных образцов, и цвет их вычисляется быстро.
Однако сейчас метод избранных координат применяется редко. Для работы на
электронных вычислительных машинах (ЭВМ) удобнее методы, близкие к методу
взвешенных координат. ЭВМ можно непосредственно включать в работу измерительного
прибора. Так, например, для измерения цвета поверхности к спектрофотометру можно
присоединить ЭВМ, в память которой заложены спектральная плотность мощности Р
λ
,
излучения стандартного источника (скажем, А) и ординаты кривых сложения в виде
произведений )( ),( ),(
λ
λ
λ
λλλ
zPyPxP . Снимаемые спектрофотометром данные о р(Я)
передаются в ЭВМ, которая производит умножение р(λ) на )( ),( ),(
λ
λ
λ
λλλ
zPyPxP ,
интегрирование трех произведений и выдает сразу х', у' и z' измеряемой поверхности при
свете источника А.
15.6. Сложение цветов.
Общая формула сложения элементарно проста. Если Ц = Ц
1
+ Ц
2
, каждая из координат
цвета Ц равна сумме соответствующих координат цветов Ц
1
иЦ
2
:
х' = x
1′
+ x
2
; y' = y
1′
+ y
2
; z' = z
1′
+ z
2
(15.17)
Правило легко обобщается для любого числа слагаемых цветов n:
∑∑∑
===
′
=
′′
=
′′
=
′
n
i
n
i
i
n
i
ii
zzyyxx
111
; ;
Такие же формулы можно написать и в системе RGB. Но далеко не безразлично, какие
значения координат подставлять в формулу (15.17) или (15.18). Пусть излучение со
спектральной плотностью мощности P
λ
прошло через фильтр со спектральным про-
пусканием τ(λ). Координаты цвета излучения в соот-ветствии с нормированием по формулам
(8.27) и (8.28) при замене р(λ) коэффициентом спектрального пропускания τ(λ) будут
∫
∫
∫
∫
∫
∫
=
′
=
′
=
′
λλ
λλλτ
λλ
λλλτ
λλ
λλλτ
λ
λ
λ
λ
λ
λ
dyP
dzP
z
dyP
dyP
y
dyP
dxP
x
)(
)()(100
;
)(
)()(100
;
)(
)()(100
.(15.19)
Если известны нормированные значения координат цвета х
ί
′, y
ί
′ и z
ί
′ нескольких
излучений, мы не можем получить координаты их суммы по формуле (15.18), что ясно хотя
бы из того, что в (15.19) величина у' – выраженный в процентах коэффициент пропускания
фильтра. При сложении он может оказаться больше ста процентов, что явно нелепо.
Для сложения нужно знать значения координат, долученных без нормирования, т. е.
∫
∫
∫
=
′
=
′
=
′
λλλτλλλτλλλτ
λλλ
dzPzdyPydxPx )()( ;)()( ;)()(
. (15.20)
Формулы (15.20) дают координаты цвета, пригодные для подстановки в формулу
(15.17) или (15.18). В Международном светотехническом словаре (39) в формулах,
аналогичных формулам (15.20), стоит не P
Λ
, а φ(λ) – спектральная плотность мощности,
выраженная в относительных единицах. Очевидно, что
φ(λ) = Р
λ
/Р
0
, (15.21)
где Р
0
– некоторая мощность, принятая за единицу.
Можно ли проводить сложение цветов, если в формулы (15.20) поставить не Рλ а φ(λ)?
Можно, но только в том случае, если мы знаем, что при расчете координат всех слагаемых
цветов Ро имело одно и то же значение. Конечно, и координаты суммарного цвета мы
получим в относительных величинах.

Заменив в формулах (15.17), (15.18), (15.20) и (15.21) координаты системы ХУZ
координатами системы RGB, мы можем проводить сложение цветов и в рамках системы
RGB.
15.7. Цвет несамосветящейся поверхности.
Как мы уже говорили, цвет предмета зависит не только от свойств его поверхности, но
и от спектралыюго состава освещающего его света. Строго говоря даже зафиксировав
спектральный состав освещения (скажем, взяв источник А), мы еще не получим
фиксированных значений его кординат: с приближением источника все координаты цвета
будут возрастать, с удалением уменьшаться. И тут о свойствах самой поверхности нам
поможет судить нормирование.
Вернемся к формулам (8.27) и (8.28) или к формулам (15.20), поставив в них р(λ)
вместо τ(λ). Найденный по этим формулам у' равен коэффициенту диффузного отражения
поверхности'. Из двух поверхностей при данной освещенности светлее будет та, у которой
больше координата у'. И так будетпря любом расстоянии от источника света до образца,
Вследствие нормирования координата у' поверхности (как и две другие координаты) не
зависит от абсолютного значения освещенности.
В данном случае знание нормированных координат несколышх цветов позволяет и
сложить эти цвета (скажем, с помощью зеркала Ламберта для двух цветов или диска
Максвелла для любого числа цветов) в соответствии с формулами (9.6) и (9.10).
Глава 16. Восприятие цвета.
16.1. Простой опыт.
Перед нами белый экран с отверстием. Через отверстие виден лист картона,
окрашенный в оранжевый цвет. Для наглядности определим цвет картона в системе:
цветовой тон λ, чистота р, коэффициенг отражения р. Пусть λ = 600 нм, р = 0,7 и р = 0,6.
Сначала яркость экрана L
э
= 10 кд·м
-2
, а яркость картона L
к
= 10 кд·м
-2
. Через отверстие
в экране мы видим оранжевый картон. Теперь увеличим освещенность экрана в 10 раз и
сразу увидим через отверстие картон уже не оранжевым, а коричневым. Изменился ли цвет
картона? Нет, не изменился. Координаты цвета картона остались прежними, в какой бы
системе их ни измерять: ведь ни поверхность картона, ни его освещение не изменились. Что
же изменилось? Наше восприятие цвета. Увеличение яркости экрана повысило уровень
адаптации глаз, и по сравнению с высоким уровнем яркости экрана яркость картона стала
низкой, он стал восприниматься намя как темный. А темно-оранжевый цвет мы и называем
коричневым.
Цвет – физическая величина, не зависящая от яркости и цвета окружающих цветной
объект предметов, от уровня адаптации зрения воспринимающего цвет человека, от его
индивидуальных свойств. От индивидуальных свойств цвет перестал зависеть с того
момента, как были приняты «Ординаты кривых сложения для стандартного
колориметрического наблюдателя МКО 1931 г.». Наука о цвете – колориметрия – это точная
наука, построенная на основе физических закономерностей и лежащая в основе многих ее
технических применений.
Иное дело восприятие цвета. Оно может сильно изменяться для одного и того же цвета
и для одного и того же человека. Изучение цветовых восприятий и ощущений – область
физиологии, психологии, эстетики.
16.2. Метамерные стимулы.
По мнению некоторых, физическая сущность цвета определяется тем, что цвет
полностью зависит от спектрального состава излучения, попадающего в глаз. И тут
возникает сомнение в том, стоит ли вообще вводить особую величину – цвет. Но дело в том,
что понятие «цвет» не совпадает с понятием «спектральный состав». Действительно, данный
спектральный состав неизбежно определяет данный цвет, но данный цвет может
обуславливаться излучениями разных спектральных составов. Одинаковость спектральных
составов для получения одного и того же цвета – условие достаточное, но не необходимое.
Как мы уже говорили, один и тот же цвет могут создавать метамерные излучения, т. е.
излучения, создающие один и тот же цвет при разных спектральных составах.
Перепишем первое из уравнений (8.28):
∫
=
′
λλλρ
λ
dxPkx )()(.
Поскольку три множителя под интегралом независимы друг от друга, х' (некоторое
определенное значение интеграла) может быть получен при самых различных комбинациях
этих множителей.
Сказанное относится, конечно, и к координатам у' и z'. Два образца могут быть
одинаковыми по цвету при различных спектральных коэффициентах отражения и
спектральных плотностях мощности. Значит, цвет не связан однозначно со спектральным
составом.
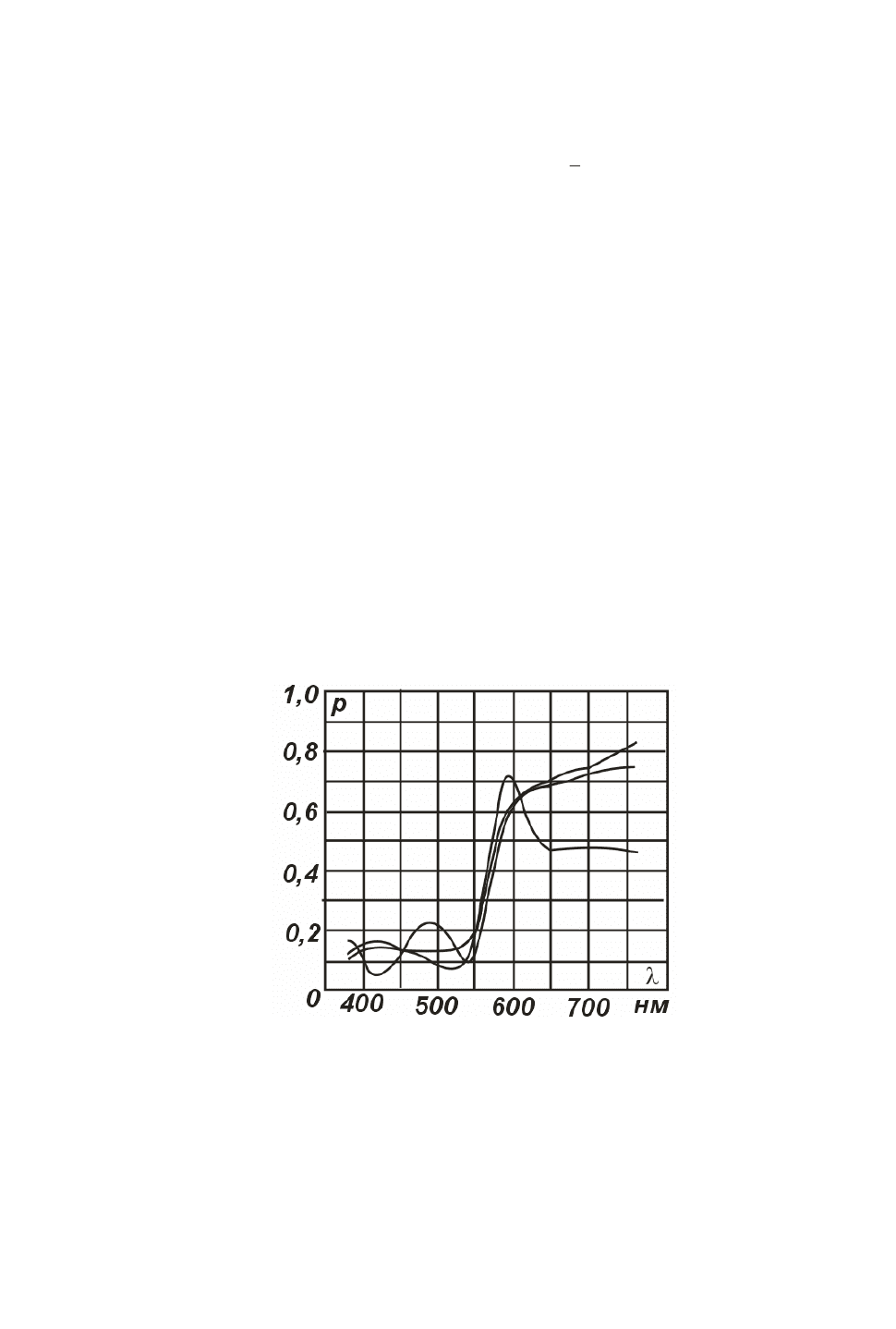
На рис. 16.1 изображены кривые спектральных коэффициентов отражения трех
образцов, обладающих при освещении источником D
65
одним и тем же цветом, т. е. дающих
метамерные стимулы.
Заметим, что при других спектральных составах освещающего света (Р
λ
) метамерные
стимулы дадут уже, как правило, различные цвета.
Возвращаясь к опыту в § 16.1, скажем, что на картоне, наблюдаемом через отверстие,
можно поместить рядом две накраски, различные по своим спектральным характеристикам,
но обладающие при данном освещении одцим и тем же цветом. Значит, мы не сможем
заметить никакой разницы между двумя метамерными оранжевьши образцамн. Поднимем
освещенность экрана в 10 раз. Желтый цвет мы теперь воспримем как коричневый, но он
будет по-прежнему одинаков у обоих образцов.
Рис. 16.1. Примеры кривых спектрального коэффициента отражения p(λ) трех
метамерных образцов.
Может показаться, что мы слишком много говорим о различии между цветом и
восприятием цвета. Но, к сожалению, некоторые авторы не видят четкой границы между
цветом и ощущением цвета, и это приводит к большим ошибкам и заблуждениям (53); см.
также (34).
16.3. Последовательный цветовой контраст.
В ясный день посмотрите на небо в окно. Потом быстро переведите взгляд на стену
комнаты. Вы увидите на ней изображение переплета окна на фоне более темных мест,
соответствующих стеклам, сквозь которые виднелось светлое небо. Явление это называется
последовательным образом.

Последовательный образ тем лучше заметен и тем дольшее сохраняется, чем ярче
предмет, на который первоначально был обращен взгляд, в особенности после прямого
взгляда на источник света. Природа явления довольно сложна, но в основном
последовательный образ появляется потому, что на месте изображения яркого предмета
израсходовались светочувствительные вещества и чувствительность сетчатки локально
понизилась. После перевода взгляда на поверхность средней яркости засвеченное место
слабее воспринимает свет, что воспринимается как пятно более темное, чем окружающий
фон.
Если яркий предмет имел ясно выраженную окраску, определенный цветовой тон,
последовательный образ виден в цвете, близком к дополнительному к цвету яркого предмета.
Это явление называется последовательным цветовым контрастом (27, 58).
Возьмем квадратную пластинку, разделенную на четыре части, каждая из которых
окрашена в один из четырех цветовз зеленый, синий, желтый, красный. Если в течение 15–20
с фиксировать взгляд на середине пластинки, а потом быстро заменить пластинку листом
белой бумаги, мы увидим на ней четыре цветных квадрата, окрашенные в цвета, близкие к
дополнительным цветам четырех квадратиков пластинки: красно-пурпурный, оранжевый,
пурпурновато-синий, сине-зеленый. Цвета последовательного контраста явно связаны с
локальной адаптацией сетчатки: направляя взгляд на другую точку бумаги, мы ясно увидим,
что вся картина перемещается по бумаге вместе с движением глаз.
16.4. Одновременный контраст.
На восприятие цвета какого-нибудь участка поля зрения влияет не только цвет, ранее
действовавший на глаз, но и цвет Поля, окружающего рассматриваемый участок. Влияние на
цве-товое восприятие цвета соседних участков поля зрения называется одновременным
цветовым контрастом (27). Если кусочки серой бумаги положить на красную и 'синюю
бумагу, они станут казаться различными. Серая бумага на красном фоне покажется
голубоватой, на синем – желтоватой. Цвет, появляющийся на серой бумаге, близок к цвету,
дополнительному к цвету фона, но, по-видимому, все же не совпадает с ним.
В некоторых случаях одновременный контраст как бы уничтожает цвет окрашенной
поверхностн, делает ее серой. Если пластинку, которая на сероватом фоне воспринимается
как светло-пурпурновато-красная (приблизительно 5RР6/4 по Манселлу), положить на ярко-
пурпурно-красный картон, пластинка покажется серой (23). В повседневной жизни мы
окружены разноцветными вещами, располагающимися на разных по цвету фонах. Взгляд
переходит с одного предмета на другой, меняется цветовая адаптация, на восприятие влияют
и одновременный и последовательный контрасты. Таким образом, ощущения, вызываемые
одним и тем же цветом, могут быть весьма различны. Но, конечно, на цветовой стимул как
на физическую величину это различие в ощущениях никакого влияния не оказывает, И тут
проявляется другая замечательная способность зрения, а которой мы сейчас расскажем.
16.5. Константность восприятия окраски.
Как мы знаем, цвет предмета обусловливается свойствами его поверхности:
спектральным апертурным коэффициентом отражения β(λ) и спектральной плотностью P
Λ
освещающего поверхность света.
Будем называть слектральный коэффициент отражения поверхнбсти данного предмета
окраской предмета (42). При изменении освещения цвет предмета меняется, окраска остается
неизменной.
Зрение необходимо нам для ориентации во внешнем мире, для различения и опознания
окружающих предметов. Опознаем мы их по форме и по цвету (яркость входит в понятие
«цвет»}. При сборе грибов мы сразу узнаем подосиновик, отличая его от поганок, сосновых
шишек, опавших листьев и прочего прежде всего по егс красной шляпке. Но для четкого
опознания предмета нам важен не его цвет, который может в широких пределах изменяться.
Важна его неизменная окраска. И вот оказывается, что человек в значительной степени

способен определять окраску предмета независимо от условий освещения. Такую
способность называют константностью восприятия окраски. Константность восприятия
окраски далеко не абсолютна, она только до известной степени приближает наблюдателя к
определению истинной окраски предмета, а иногда вообще отказывает. Но замечательная
способность вносить коррективу в непосред-ственно воспринимаемый цвет, поправки на
особенности данного освещения – эта способность безусловно существует и подтверждается
многими экспериментами. Существует она и у многих животных, не только у позвоночных,
но даже у насекомых (например, у пчел). Несомненно, что константность восприятия
окраски биологически чрезвычайно полезна, но для ее выработки природе потребовалось
создать и развить чрезвычайно сложный механизм. Сущность его заключается в том, чтобы
при каждом конкретном освещении учитывать его спектральный состав и пересчитывать
воспринимаемый цвет, приводя его к какому-то одному, привычному для организма
стандарту. Выходит, что у каждого из нас есть свой стандартный источник цвета и, приводя
любой воспринимаемый цвет к этому стандарту, мы определяем окраску предмета, его
индивидуальные свойства.
Что же может служить отправной точкой для такого пересчета? Очевидно, цвет
известного нам предмета, с которым мы сравниваем излучения, исходящие от других
предметов, что и помогает определить их окраску. Пересчет облегчается, если в поле зрения
есть белый предмет, который, неселективно отражая нзлучение источника, дает возможность
судить о характеристиках освещения. Хорошо известные белые предметы – побеленная
стена или потолок, бумага, сахар, снег. Но, видимо, поправку можно вносить и по
окрашенным, хорошо знакомым нам предметам.
Таким образом, в основе конетантности восприятия окраски лежит сложнейший
механизм, работы которого мы, однако, не ощущаем. Он срабатывает автоматически, и мы
осознаем только готовый результат его работы – восприятие окраски.
16.6. Высшая метрика цвета.
Почти 60 лет тому назад знаменитый австрийский физик Эрвин Шредингер (1887–
1961) предложил разграничить две существенно различные области цветоведения (68).
Высказанная ученым идея настолько важна, что мы считаем уместным выразить ее его
собственными словами, приведя довольно длинную цитату:
«Оказалось, что все опыты по измерению цветов распадаются на две принципиально
различные группы в зависимости от того, используется ли в качестве критерия для установки
прибора полное равенство (неразличимость) двух граничащих цветных полей или еще
другие критерии (различимость полей, максимальное сходство, сильнейший контраст).
Результаты измерений первого рода образуют замкнутую в себе единую систему, простые
закономерности которой известны формально со времен Грасмана и фактически со времени
Кенига. Я думаю, что уместно систему этих закономерностей – обычно называемую
законами смешения светов – отличать как низшую метрику цветов от гораздо более
запутанной и намного менее известной высшей метрики цветов, нмеющей дело с
результатами измерений второго рода.
Я считаю строгое различие между этими двумя областями – несмотря на то, что
теоретически они тесно соприкасаются – потому чрезвычайно важным, что иначе
многочисленные неясности в понятиях и акспериментальные неопределенности, которые мы
встречаем в высшей метрике цветов на каждом шагу, постоянно угрожают проникновением
в низшую метрику, внося в нее путаницу, тогда как последняя сама по себе прочна и надежна
и никак не затрагивается этими затруднениями».
Итак, низигая метрика цвета – это чисто физическая наука колориметрия.
Высшая метрика цвета уже, несомненно, тесно связана с нашими ощущениями, нашим
восприятием цвета. Поэтому высшая метрика цвета привлекает внимание психологов,
физиологов. Но разрабатают ее и физики, светотехники, колориметристы, математики.
Нужно сказать, что обе метрики цвета отнюдь не зависимы друг от друга. Истоки

колориметрии лежат в области цветовых ощущений, которые, как и другие ощущения, дают
нам сведения о внешнем материальном мире. Примером связи обеих метрик может служить
опыт с размещением цветных карточек, описанный нами в § 4.2. На основе наших ощущений
мы установили трехмерность цвета – одно из фундаменталышх положений колориметрии.
Решение многих практически важных задач требует разработки вопросов, относящихся
к высшей метрике цвета. Одна из таких задач, например, построение атласа цветов.
Определение порогов различения цветов необходимо для установления обоснованных
допусков на цвет многих товаров. Поэтому к области высшей метрики цвета относится
много работ, авторы которых стремятся придать ей характер строгой, математически
обоснованной науки. Проблемам высшей метрики цвета посвящена следуюшая глава.
Глава 17. Пороги цветоразличения и равноконтрастные системы.
17.1. Различение цветностей.
Попробуем ввести понятие порога цветоразличения по аналогии с пороговым
различением яркостей. Введенную нами в главе 2 формулу (2.7), проведя в ней замену L – L
п
на ∆L, перепишем в виде
L
L
K
Δ
= . (17.1)
Приближая яркость L
п
к яркости L, мы в конце концов придем к такому значению ∆L,
при котором разница между двумя яркостями станет едва заметной, т. е. дойдет до порога
различения яркостей: ∆L
п
.
Подобным образом приближая цвет Ц
1
к цвету Ц
0
, мы дойдем до такой разности ∆Ц
п
равной Ц
1
– Ц
0
, при которой разница в цвете будет едва заметна.
Мы знаем, что пороговая разность яркостей ∆L
п
возрастает с ростом яркости l, что,
однако, не означает падения чувствительности глаза к различению яркостей с ростом
яркости. Решающее значение имеет не абсолютная величина ∆L
п
, а ее отношение к исходной
яркости L, т. е. контраст К, а точнее, по-роговый контраст К
п
. Порог цветоразличения ∆Ц
п
тоже растет с увеличением Ц
0
,
Но у ∆Ц
п
сразу обнаруживается существенное отличие от порога ∆L
п
. Яркость –
величина скалярная, а цвет – вектор. Поэтому порог цветоразличения – тоже вектор, т. е. его
следует характеризовать не только модулем, но и направлением. В пространстве от точки,
изображающей конец вектора Ц
0
, можно провести бесчисленное множество векторов ∆Ц
п
в
различных направлениях. Оказывается, что модули этих векторов будут различны. Построив
поверхность, охватывающую концы всех векторов ∆Ц
п
, мы получим некоторый объем.
Цвета, концы векторов которых лежат внутри этого объема, для глаза неотличимы от цвета
Цо. Приближенно полученный объем можно рассматривать как трехосный эллипсоид.
Минимальную, еще уловимую разницу в цвете называют порогом цветоразличения.
Чтобы в какой-то мере провести аналогию с пороговым контрастом яркости, перейдем
от цвета к цветности, т. е. разделим координаты цвета Ц
0
на х' + Y' + z' и отложим
интересующие нас величины на графике ху. Эллипсоид изобразится эллипсом, в центре
которого будет цветность С
0
, соответствующая цвету Цо. Внутри эллипса лягут цветности,
неотличимые от Со Проведя из точки С
0
прямую до любой точки эллипса, назовем
полученный отрезок ∆l.
