Луцко А.Н., Марцулевич Н.А. и др. Механика
Подождите немного. Документ загружается.

251
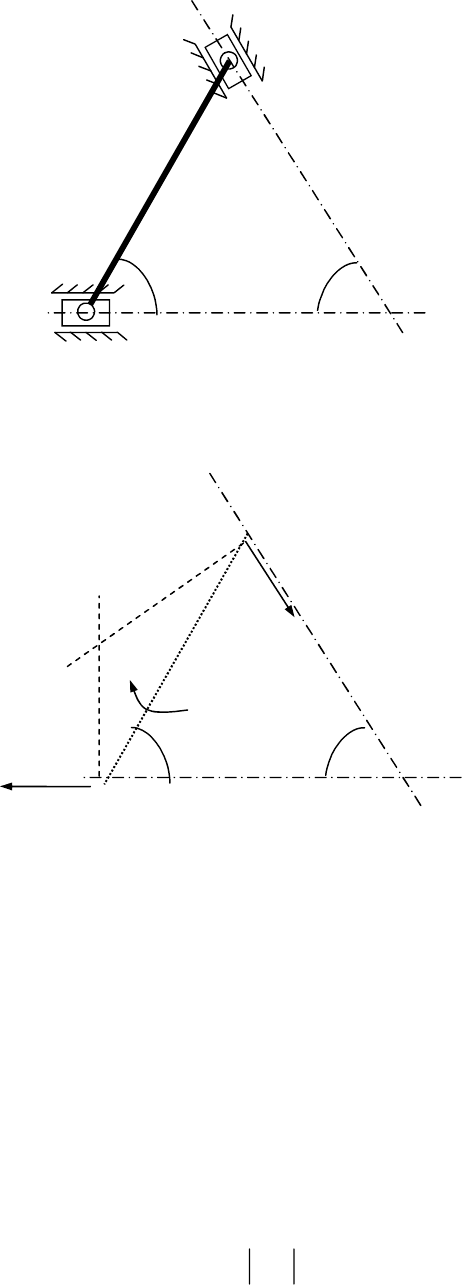
Пример решения.
Определим скорость и ускорение
ползуна В, угловую скорость и угловое
ускорение шатуна АВ по известной
скорости и ускорению ползуна А (см.
рисунок).
Исходные данные: длина шатуна
АВ равна 4 м; V
A
= 1 м/с; W
A
= 3 м/с
2
.
Решение. Шатун совершает
плоскопараллельное движение
(подраздел 3.4.). Направление
векторов скорости ползунов А и В
известны: они движутся вдоль направляющих. Восстановим
перпендикуляры к векторам скоростей ползунов. Точка пересечения
перпендикуляров даст положение мгновенного центра скоростей Р
(см. рис.). Следовательно,
V
A
= ω
AB
IAPI и V
В
= ω
AB
IPВI, где
ω
AB
– угловая скорость шатуна АВ.
Из решения треугольника АВР
находим:
I API = IPВI = 4/√ 3. Тогда
ω
AB
= V
A
/ IAP I = √ 3 /4 с
-1
, а V
В
=
1 м/с. Перейдем к определению
ускорения
W
B
ползуна В и углового
ускорения шатуна ε
АВ
. Для этого
воспользуемся формулой сложения
ускорений при плоскопараллельном
движении твердого тела (см.
подраздел 3.4), взяв теперь в качестве полюса точку А. Тогда имеем:
W
B
= W
А
+ W
BА
,
где W
BА
– ускорение точки В в ее вращательном движении вокруг
полюса А. Последнее, в соответствии с формулой (3.15), является
суммой касательного ускорения
W
m
и нормального ускорения W
n
. Все
четыре ускорения связаны векторным соотношением:
W
B
= W
А
+ W
m
+ W
n
(♠)
Нормальное ускорение в нашем случае направлено вдоль шатуна к
точке А. Его величина согласно (3.26) равна:
АВW
АВn
2
3/4 м/с
2
.
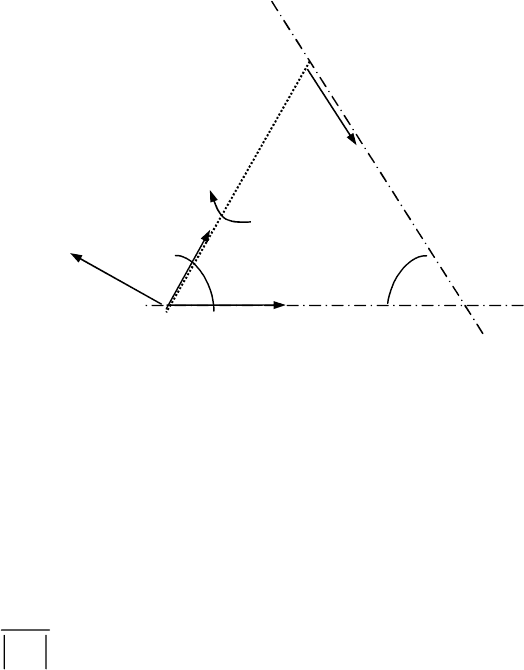
Вектор касательного ускорения W
m
перпендикулярен шатуну АВ.
Отметим на рисунке направления всех ускорений. При этом
направления векторов
W
B
и W
m
пока что не могут быть определены
A
B
60
º
60
º
V
A
Р
A
B
60
º
60
º
V
B
ω
АВ
252
однозначно, поскольку неизвестно, ускоренным или замедленным
является поворот шатуна.
Спроектируем равенство (♠)
на горизонтальную и
вертикальную оси:
W
B
= W
A
sin30
0
– W
m
cos30
0
+
+ W
n
cos60
0
;
0 = -W
A
cos30
0
+ W
m
sin30
0
+
+ W
n
sin60
0
.
Получили два уравнения
относительно неизвестных
W
B
и W
m
. Последовательно решая эти
уравнения, получаем:
W
m
= 9√3/4 м/с
2
и W
B
= -(15 - 3√3)/8 м/с
2
.
Отрицательное значение ускорения означает, что его истинное
направление противоположно первоначально принятому (см. рис.).
Угловое ускорение шатуна ε
АВ
найдем с помощью формулы (3.25):
AB
W
m
АВ
9√3/16 с
-2
.
Ответ: V
В
= 1 м/с; W
B
= (15 - 3√3)/8 м/с
2
; ω
AB
= √ 3 /4 с
-1
; ε
АВ
=
9
√3/16 с
-2
.
Контрольная работа № 3.
Динамика
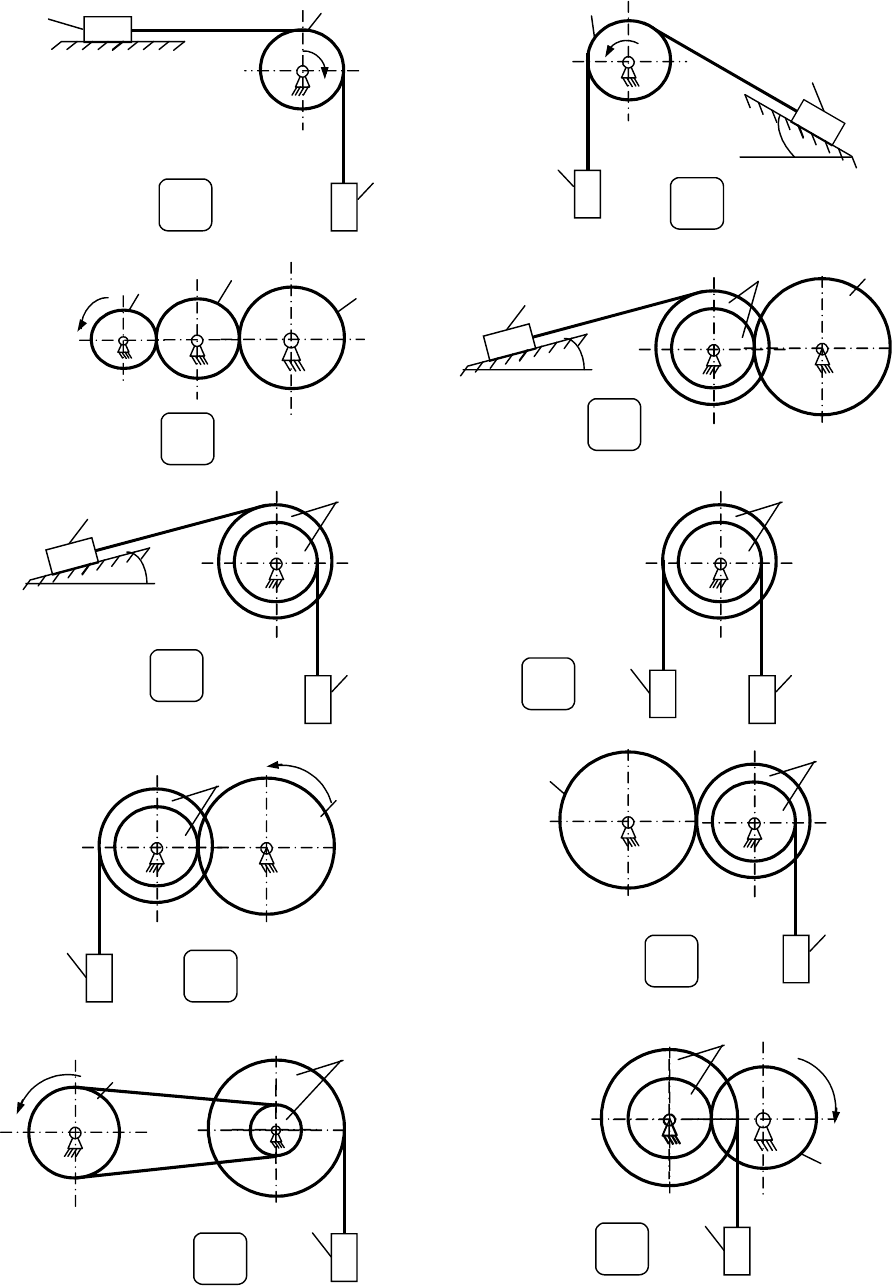
В приведенных ниже расчетных схемах механическая система
состоит из трех тел. Движение тел происходит либо за счет
приложенного вращающего момента, либо за счет веса груза. С
помощью теоремы об изменении кинетической энергии механической
системы требуется найти ускорение всех трех тел.
В таблице исходных данных приняты следующие обозначения:
m –
масса тела; R и r – радиусы большого и малого барабана
соответственно;
f – коэффициент трения скольжения; α – угол
наклона поверхности, по которой перемещается груз;
M – вращающий
момент.
W
n
W
m
W
A
A
B
60
º
60
º
W
B
ε
АВ
253
Сила и коэффициент трения скольжения связаны соотношением:
F
тр
= f ∙ N, где N – проекция веса тела на нормаль к поверхности
(см.подраздел 2.8).
Расчетные схемы
3
2
2
1
M
3
4
r
2
1
α
3
5
r
2
1
1
3
α
r
2
3
3
7
r
2
1
1
6
r
2
3
M
1
8
2
3
M
3
9
2
1
M
α
3
1
2
1
M
0
r
M
2
1
3
254
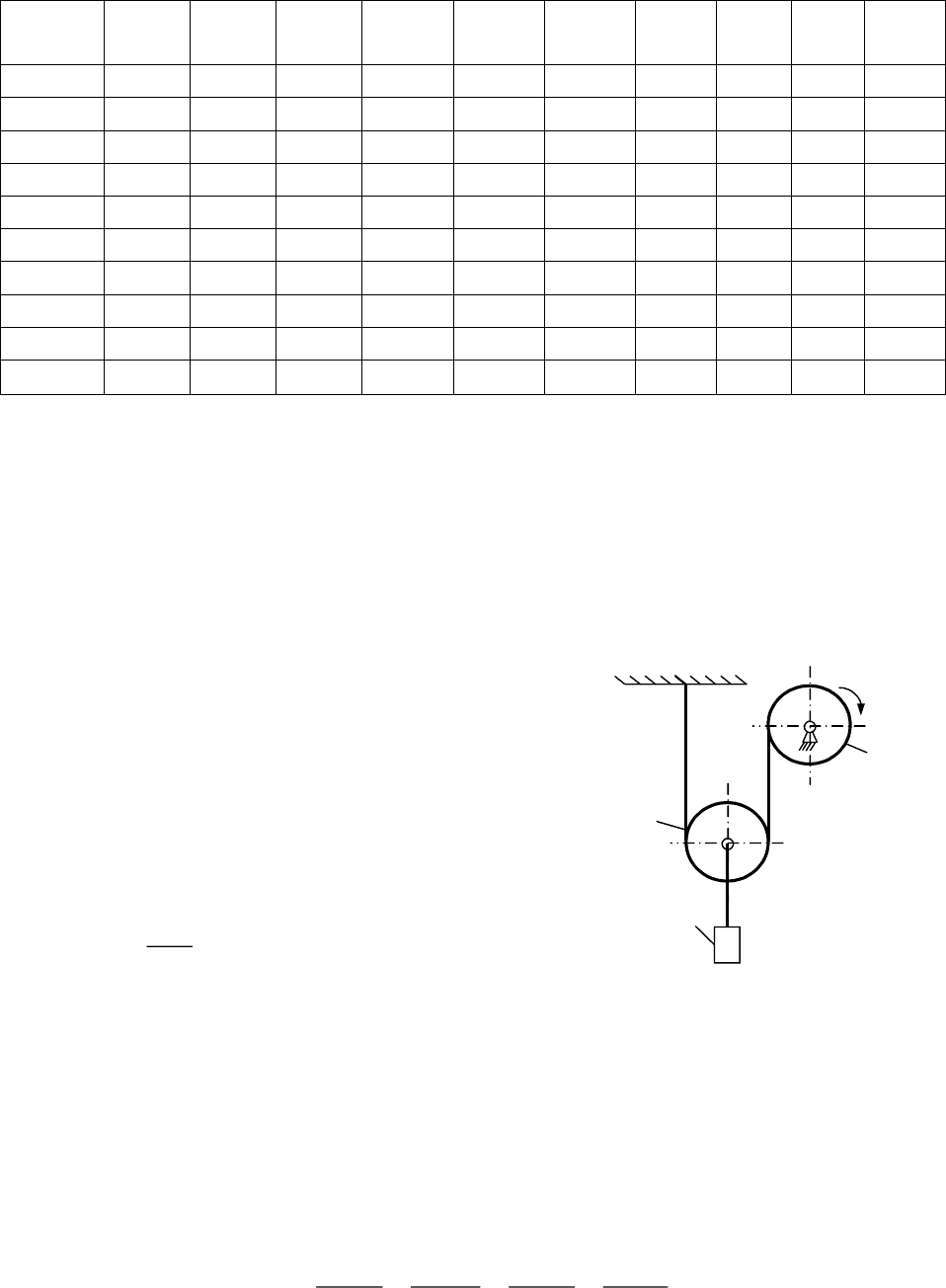
Исходные данные
№
вар.
m
1
,
кг
m
2
,
кг
m
3
,
кг
R
1
,
см
R
2
,
см
R
3
,
см
r
2
,
см
f
α,
◦
M,
Н∙м
0 20 10 40 30 45 60 25 0,12 30 70
1 24 40 20 35 50 80 30 0,15 15 40
2 15 35 42 15 55 75 35 0,20 45 120
3 20 8 15 45 60 70 40 0,10 60 60
4 10 20 50 20 55 65 20 0,25 20 220
5 45 20 15 30 40 50 15 0,15 40 90
6 20 30 50 40 50 85 25 0,20 35 480
7 15 30 70 25 45 45 30 0,12 25 180
8 40 20 100 20 60 40 40 0,25 50 270
9 15 32 30 25 40 55 20 0,10 55 100
Пример решения.
Определим ускорение груза 1 в механической системе,
изображенной на рисунке. Нити невесомы и нерастяжимы.
Исходные данные: m
1
= 40 кг; m
2
= 10 кг; m
3
= 20 кг; R
2
= 20 см; R
3
= 50 см; М = 100 Н∙м.
Решение. Данная механическая система
состоит из трех движущихся тел: груза 1,
блока 2 и барабана 3. Согласно (4.52)
производная по времени от кинетической
энергии механической системы равна
алгебраической сумме мощностей всех сил,
вызывающих движение:
n
i
i
N
d
dT
1
(♣)
Определим левую и правую части этого равенства. Кинетическая
энергия системы
Т включает энергию поступательного движения
груза, энергию вращательного движения барабана и кинетическую
энергию блока, который будет совершать и поступательное, и
вращательное движение. С учетом формул (4.48)
– (4.50) для
кинетической энергии всей системы имеем:
2
2
2
2
2
33
2
22
2
22
2
11
J
JVmVm
Т
.
3
1
2
M

255
Моменты инерции блока и барабана равны (см. подраздел 4.6):
2,0
2
2
22
2
Rm
J
кг∙м
2
;
5,2
2
2
33
3
Rm
J
кг∙м
2
.
В выражении для кинетической энергии выразим все скорости
через скорость груза. Скорости поступательного движения груза и
блока одинаковы:
V
1
= V
2
= V. Угловые скорости вращения блока и
барабана, очевидно, связаны соотношением: ω
3
R
3
= 2 ω
2
R
2
, откуда с
учетом численных значений радиусов ω
3
= 0,8 ω
2
. В свою очередь ω
2
= V/ R
2
. Подставляя последние соотношения в выражение для
кинетической энергии, получаем следующую связь энергией и
скоростью груза: Т = 47,5 V
2
.
Раскроем теперь правую часть (♣). Для этого рассмотрим
действующие в системе силы и их мощности. Мощность будут иметь
сила тяжести груза
– N
1
, сила тяжести блока - N
2
и вращающий
момент
– N
3
. Используя формулы (4.35) и (4.41), имеем:
N
1
= m
1
g V = 400 V; N
2
= m
2
g V = 100 V; N
3
= M ω
3
= 400 V.
Подставим полученные выражения в (♣), продифференцируем и
сократим на
V. В результате для ускорения груза получим:
d
dV
W
9,47 м/с
2
.
Ответ: W
1
= 9,47 м/с
2
.
Контрольная работа № 4.
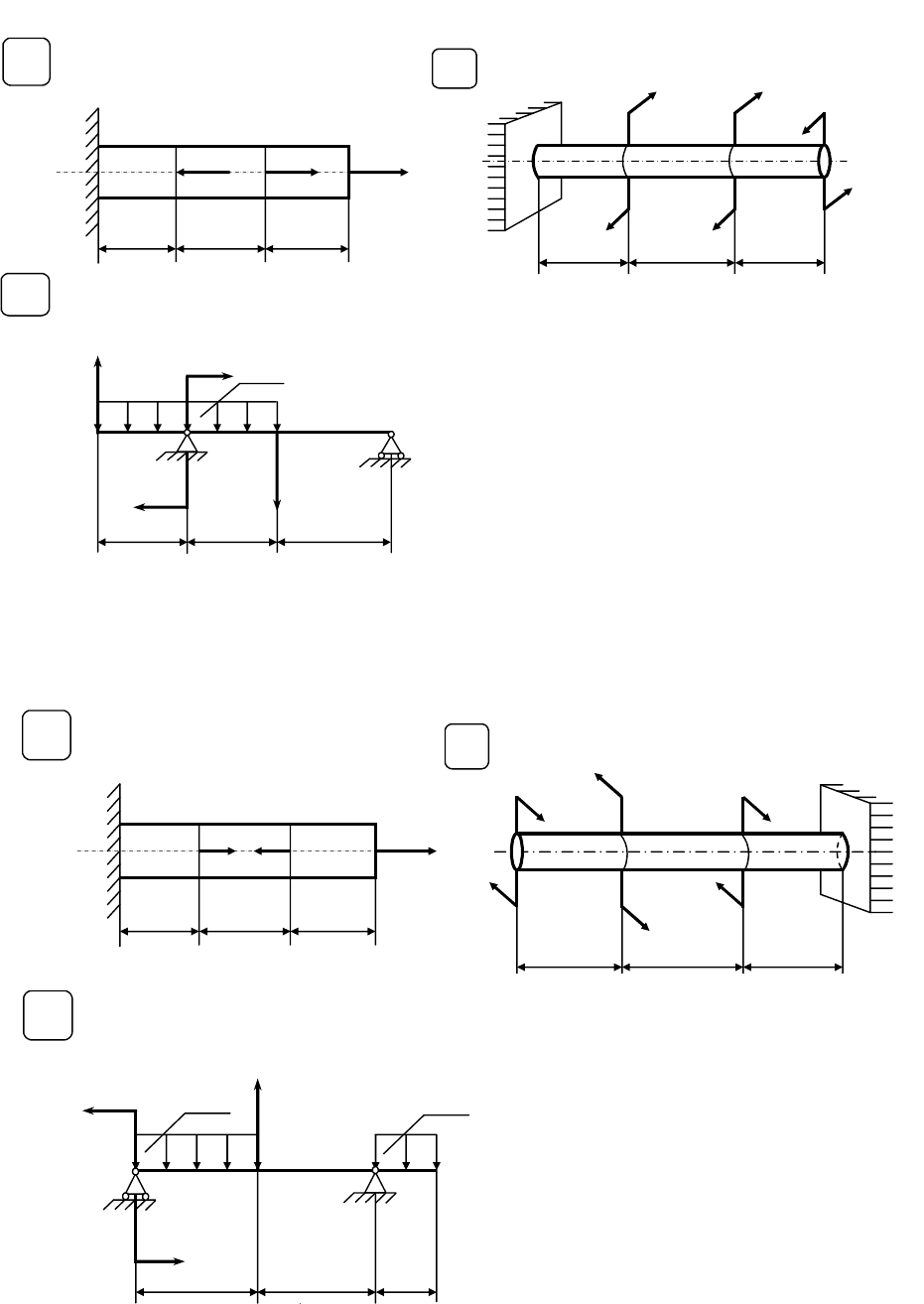
Внутренние силовые факторы в элементах химического оборудования
Настоящая контрольная работа состоит из трех задач. В первой
задаче для стержня, подвергнутого растяжению
– сжатию, необходимо
составить аналитическое выражение для продольной силы
N на
каждом грузовом участке и построить ее эпюру. Во второй задаче для
вала, подвергнутого кручению, необходимо определить значение
скручивающего момента Т
0
или момента в заделке, на всех грузовых
участках составить аналитические выражения для крутящих
моментов, вычислить их значения и построить эпюру. В третьей
задаче требуется для двухопорной балки определить ее опорные
реакции, получить выражения для поперечной силы
Q и изгибающего
момента
M на каждом грузовом участке, вычислить их экстремальные
значения и построить эпюры.
256
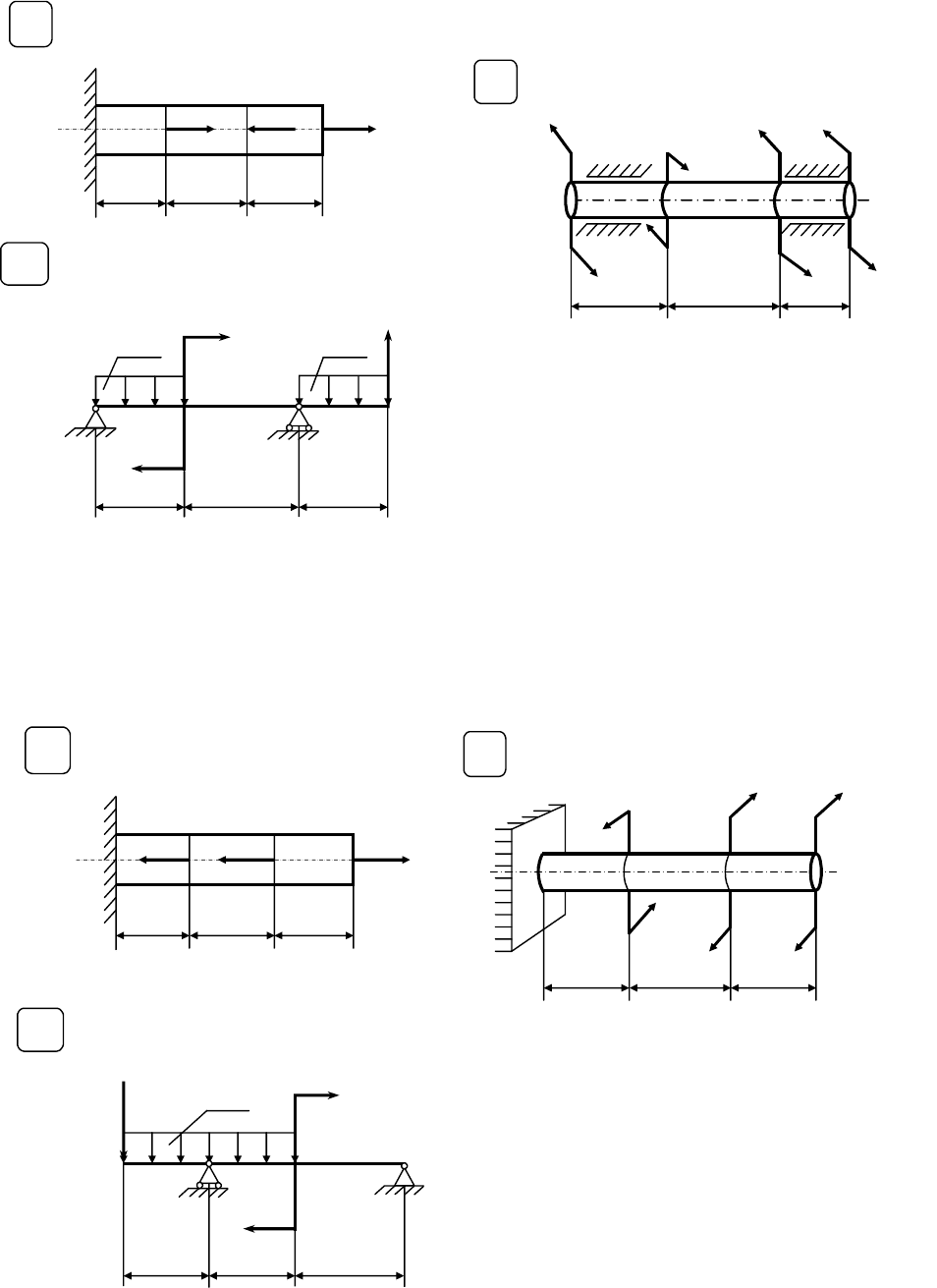
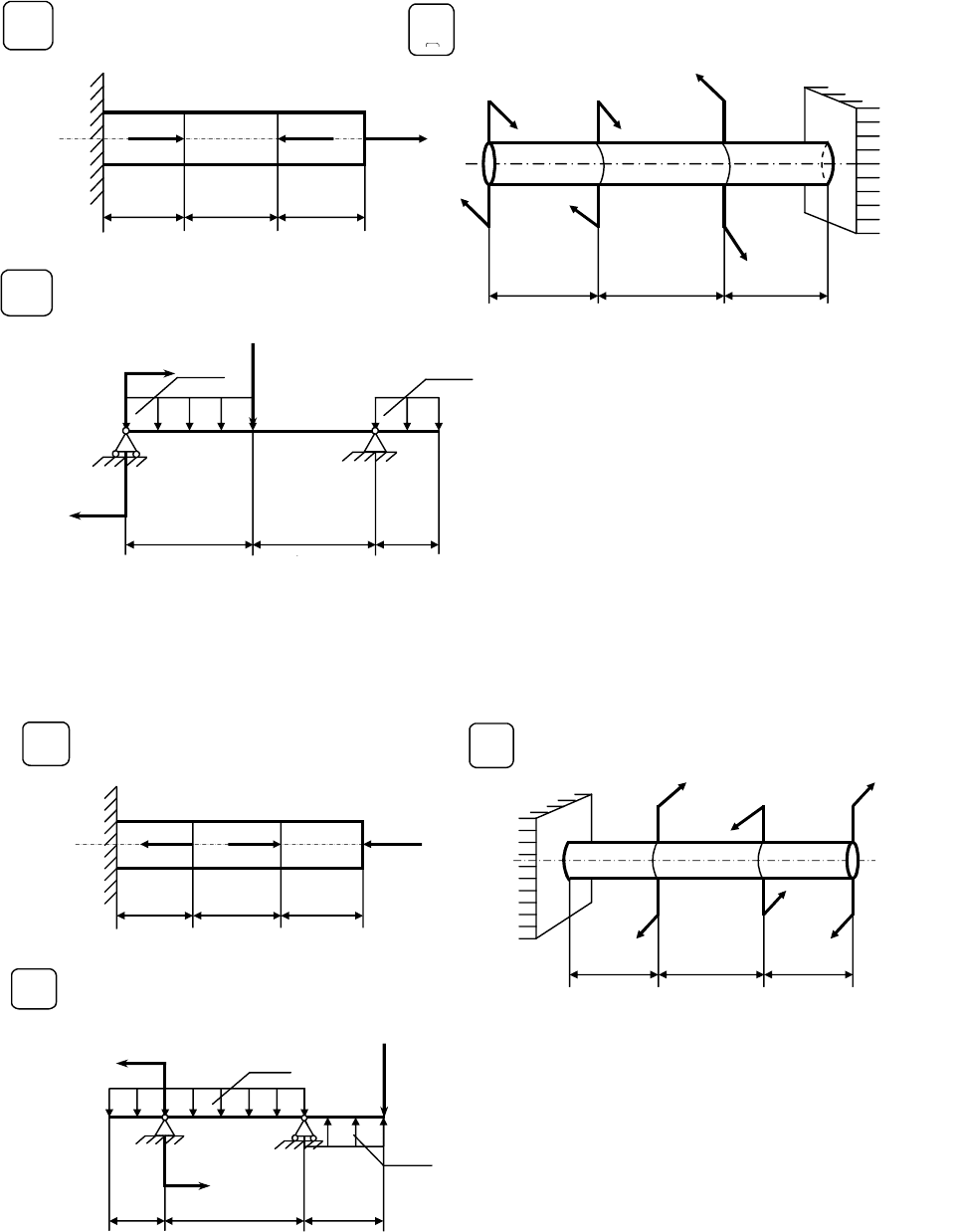
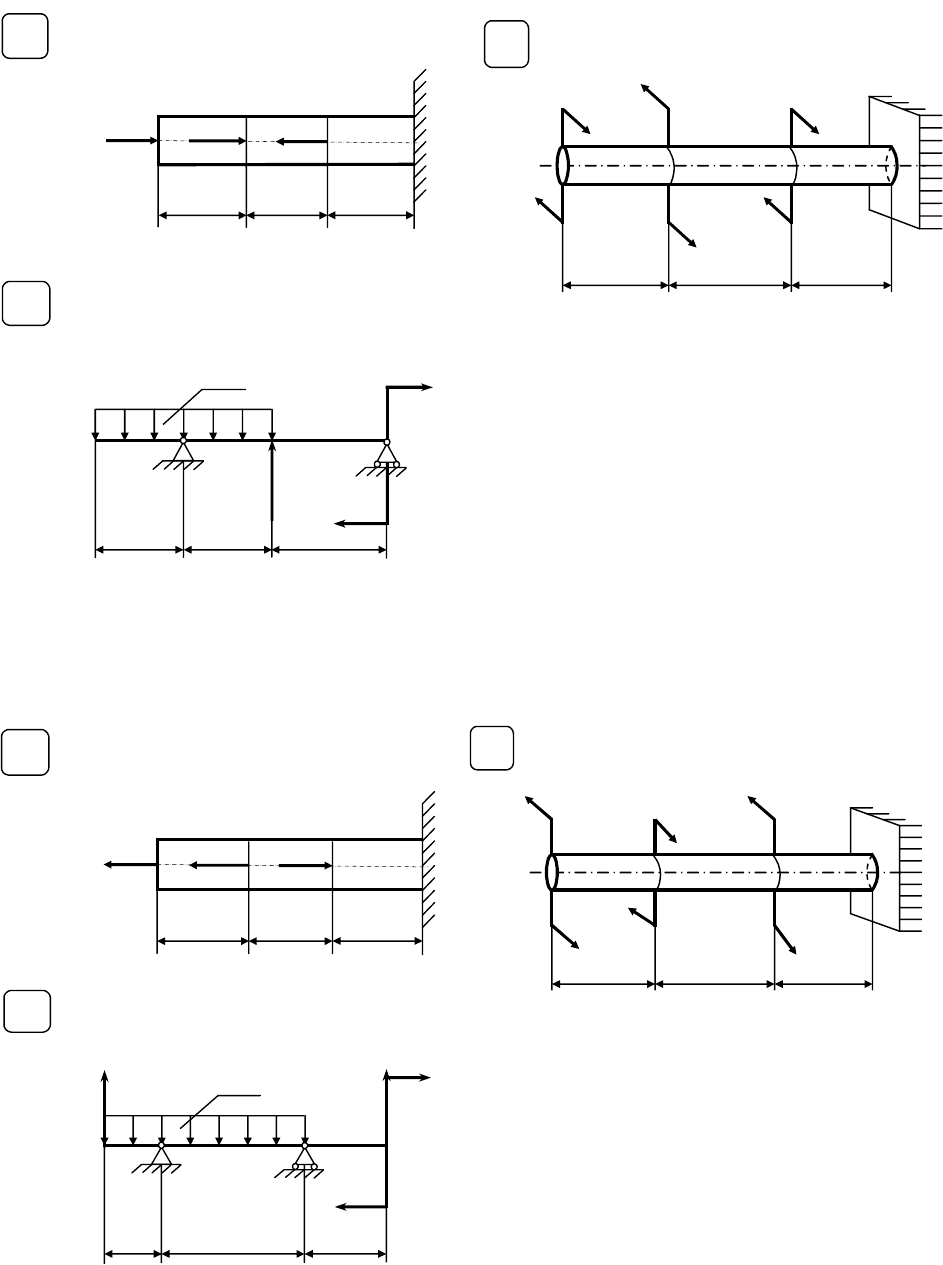
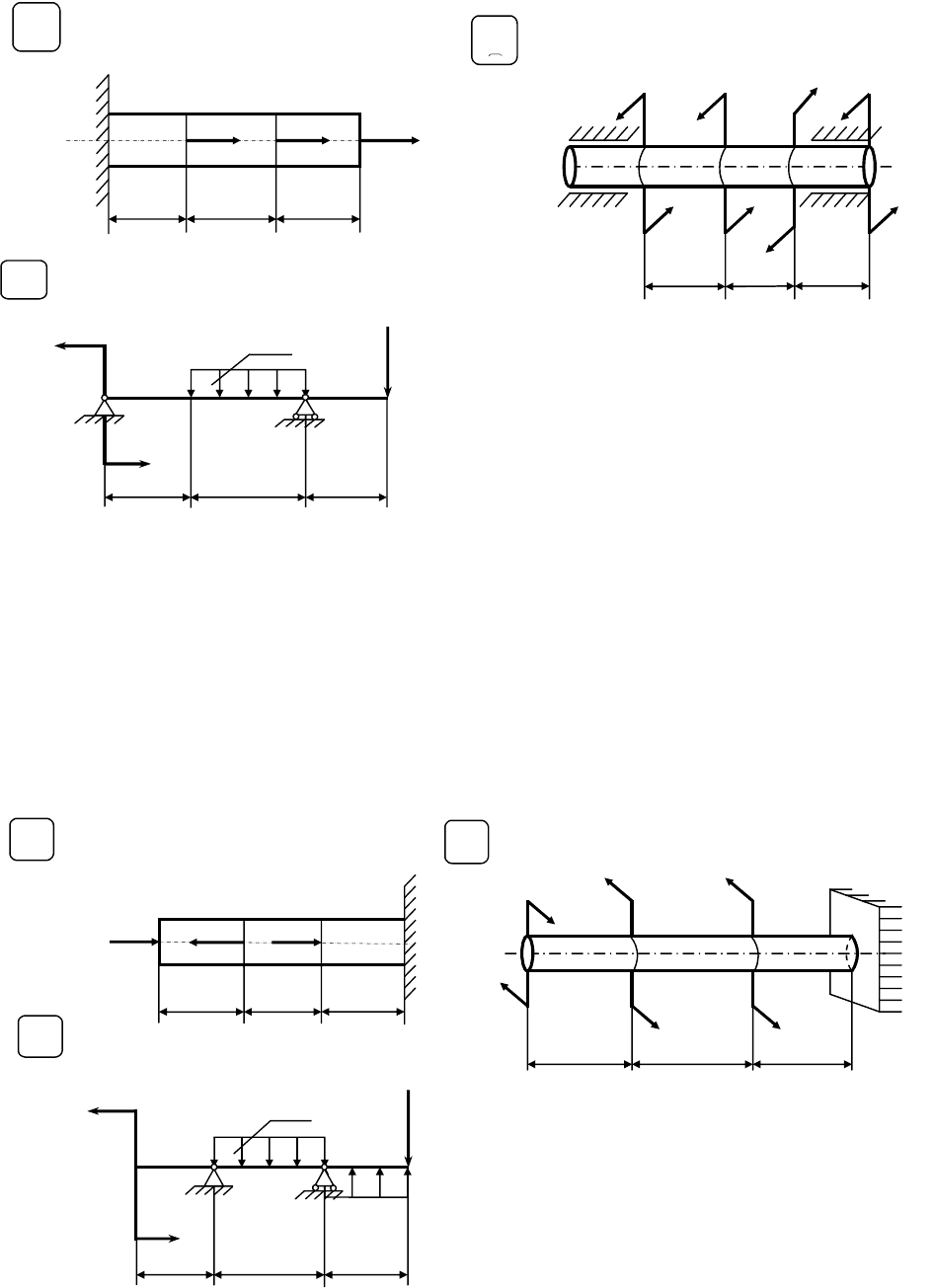
Варианты расчетных схем
1
3
l
2
l
1
l
1
F
2
F
3
F
3
1
F
3
F
3
q
1
l
3
l
2
l
3
M
2
Вариант № 0
1
l
2
l
3
l
1
M
2
M
3
M
1
3
l
2
l
1
l
1
F
2
F
3
F
2
Вариант № 1
3
l
2
l
1
l
3
M
2
M
1
M
3
2
F
3
q
2
q
1
l
3
l
2
l
2
M
257
1
3
l
2
l
1
l
1
F
2
F
3
F
3
1
l
3
M
3
q
1
q
2
l
3
l
2
Вариант 2
3
l
2
l
1
l
2
M
3
M
0
M
1
M
1
3
l
2
l
1
l
1
F
2
F
3
F
3
3
F
3
q
1
l
3
l
2
l
3
M
2
Вариант № 3
1
l
2
l
3
l
1
M
2
M
3
M
258
1
3
l
2
l
1
l
1
F
2
F
3
F
3
3
M
1
q
3
q
1
l
3
l
2
l
3
F
2
1
Вариант № 4
3
l
2
l
1
l
3
M
2
M
1
M
1
3
l
2
l
1
l
1
F
2
F
3
F
3
2
q
1
F
1
q
1
l
3
l
2
l
3
M
2
Вариант № 5
1
l
2
l
3
l
1
M
2
M
3
M
259
1
3
l
1
F
2
l
1
l
2
F
3
F
3
1
q
1
l
3
l
2
l
2
M
2
F
2
Вариант № 6
3
l
2
l
1
l
3
M
2
M
1
M
1
3
l
1
F
2
l
1
l
l
2
F
3
F
3
1
F
3
q
1
l
3
l
2
l
2
M
2
F
2
Вариант № 7
3
l
2
l
1
l
3
M
2
M
1
M
260
1
3
l
2
l
1
l
1
F
2
F
3
F
3
3
F
1
q
1
l
2
l
3
l
3
M
2
Вариант № 8
3
l
l
2
l
1
l
1
M
0
M
1
M
2
M
1
3
l
1
F
2
l
1
l
2
F
3
F
3
1
F
3
l
1
l
2
l
3
M
2
q
2
Вариант № 9
3
l
2
l
1
l
3
M
2
M
1
M
