Липин А. (ред) Интенсификация тепловых и массообменных процессов в гетерогенных средах
Подождите немного. Документ загружается.

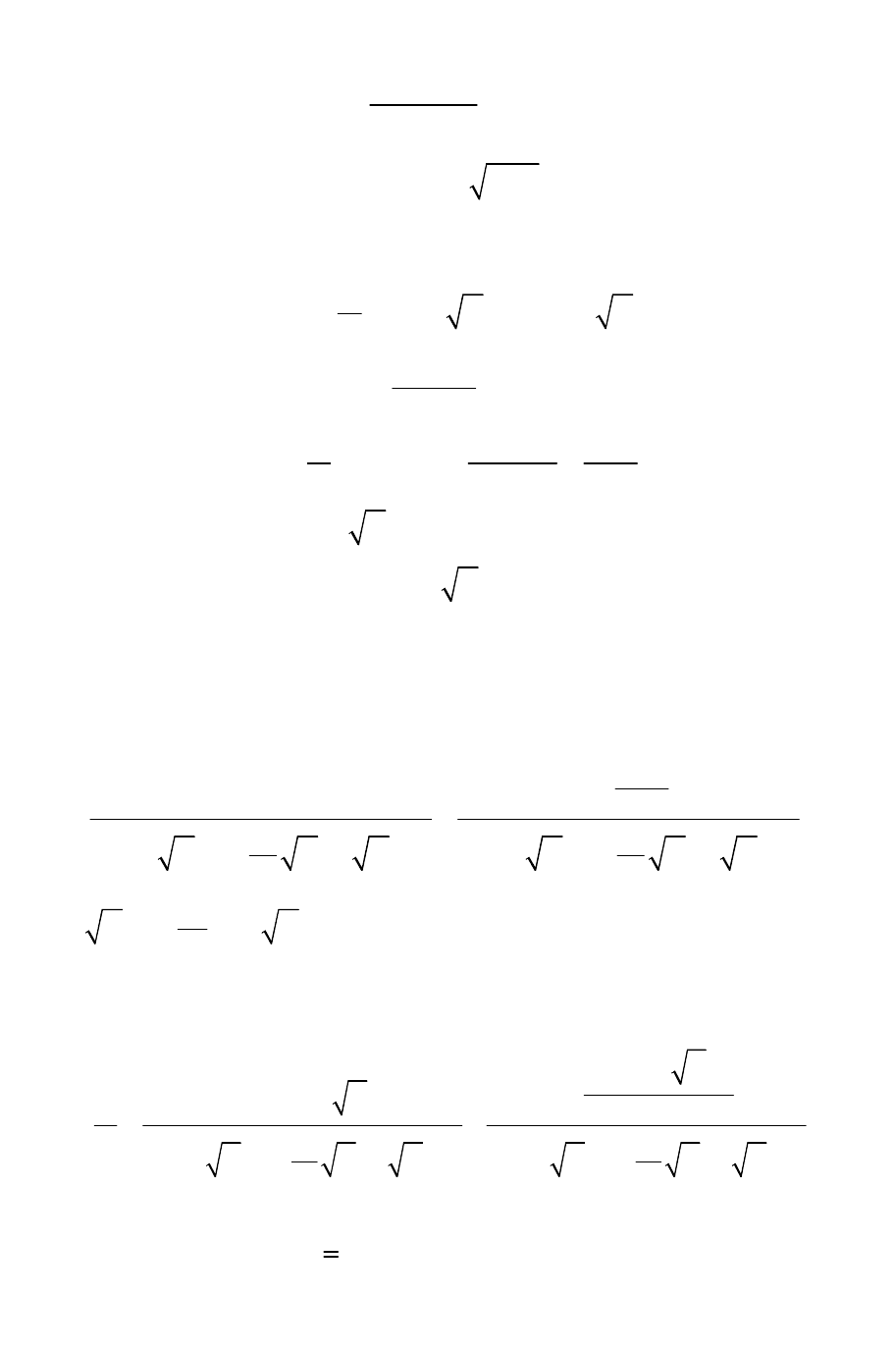
151
При этом поток теплоты с поверхности цилиндра за счет испарения
влаги определяется следующим выражением:
()
( )
(
)
{
( )
}
2
0
1exp0,5
0,5
0,51.
m
pmm
m
mm
Bi
qruuFoBi
Bi
erfcBiFo
**
é
éù
t=br---´
ê
êú
ëû
-
ë
ù
éù
´--
ú
ëû
û
(131)
Применив в уравнениях (126)–(129) преобразование Лапласа,
получим:
( )
(
)
(
)
0
00
,;
t
trsAIprBKpr
s
-=+ (132)
(
)
0,
0;
ts
r
¶
=
¶
(133)
( )
(
)
(
)
,
,,
c
tRsqs
t
HtRs
sr
¶
éù
-=+
êú
¶l
ëû
(134)
В выражении (132)
(
)
0
Ipr
- модифицированная функция Бесселя
первого рода нулевого порядка,
(
)
0
Kpr
- функция Бесселя второго рода
нулевого порядка от мнимого аргумента.
Определив с помощью граничных условий постоянные в уравнении
(132), будем иметь:
( ) ( )
()
( ) ( )
0
0101
0;
,
11
c
B
qs
s
tt
H
A
sIpRpIpRsIpRpIpR
HH
=
×
-
l
=-
éùéù
++
êúêú
ëûëû
(135)
где
(
)
(
)
10
.
dr
IpRIpR
d
éù
=
ëû
Подставляя (135) в выражение (132), получаем решение краевой
задачи (126)–(129) в области изображений:
( )
( )
( )
( ) ( )
(
)
(
)
( ) ( )
0
00
0
0101
,.
11
c
qsIpR
s
ttIpR
t
H
trs
s
sIpRpIpRsIpRpIpR
HH
×
-
l
-=-
éùéù
++
êúêú
ëûëû
%
%
(136)
Выражение (136) в правой части содержит отношения обобщенных
полиномов относительно
S
и вследствие этого удовлетворяет условиям
второй теоремы разложения. Использовав, как и ранее, свойство
линейности обратного преобразования Лапласа, запишем:
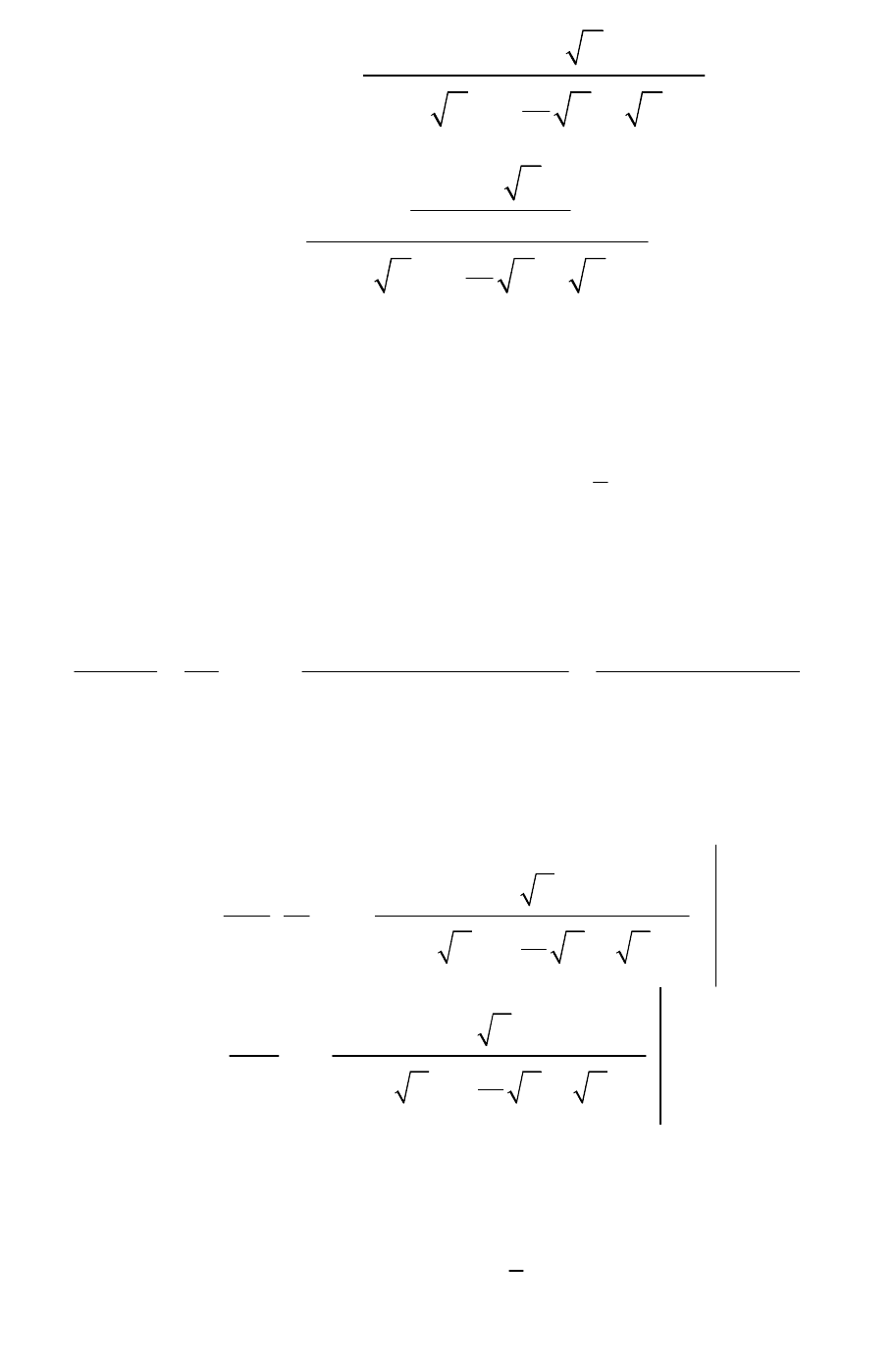
152
( )
( )
( )
( ) ( )
()
( )
( ) ( )
00
1
0
01
0
1
01
,
1
.
1
c
ttIpR
trtL
sIpRpIpR
H
qsIpR
s
H
L
sIpRpIpR
H
-
-
ìü
ïï
-
ïï
t-=-
íý
éù
ïï
+
êú
ïï
ëû
îþ
ìü
ïï
×
ïï
l
-
íý
éù
ïï
+
êú
ïï
ëû
îþ
(137)
Обратное преобразование от первого слагаемого правой части
выражения (137) имеет вид:
( ) ( ) ( )
( )
1
12
000
1
~exp.
ccnnn
n
LttttAIrFo
¥
-
=
éù
=---m-m
êú
ëû
å
(138)
Здесь
n
m
- корни характеристического уравнения:
(
)
( )
(
)
( ) ( ) ( )
( )
01
2222
1
001
2
2
;,
nn
n
n
n
nnnnn
II
Bi
A
IBi
IBi
II
mm
m
===
méù
mm+
mm+m
ëû
(139)
где
(
)
0
I
m
- функция Бесселя первого рода нулевого порядка.
Для того чтобы выполнить обратное преобразование второго
слагаемого, применим теорему Дюамеля, согласно которой получаем:
()
( )
( ) ( )
2
0
11
01
0
~
1
t
IpR
qt
LLdt
H
sIpRpIpR
H
t
--
t-
æö
éù
ç÷
êú
éù
¶
ç÷
êú
=×+
êú
l¶t
éù
ç÷
êú
ëû
+
ç÷
êú
êú
ëû
ëû
èø
ò
()
( )
( ) ( )
0
1
01
0
.
1
IpR
q
L
H
sIpRpIpR
H
-
t=
éù
êú
t
êú
+
l
éù
êú
+
êú
êú
ëû
ëû
(140)
Обратное преобразование величины, стоящей в квадратных скобках
выражения (140), аналогично (138) для случая, когда
0
1,0.
c
tt
==
Поэтому
можно записать, что:
[]
( )
( )
12
0
1
~1exp.
nnn
n
LAIrFo
¥
-
=
=-m-m
å
(141)
При этом:

153
[]
( )
1
0
0
1
~1.
nn
n
LAIr
¥
-
t=
=
=-m
å
(142)
Выполнив дифференцирование в (141) по t, будем иметь:
[]
( )
( )
1
2
2
0
2
1
~
exp.
n
nnn
n
L
a
AIrFo
R
¥
-
=
¶
m
=m-m
¶t
å
(143)
Подставляя выражения (141)–(143) в (140) и меняя пределы
интегрирования, окончательно получаем:
()
( )
( )
()
( )
() ()
( )
( )
( )
()
2
2
122
0
2
1
0
00
11
222
0
1
0
~expexp
1
expexp.
n
nnnn
n
nnnn
nn
Fo
nnnnn
n
qt
a
LAIrFoFodt
H
R
qqq
AIrAIr
HHH
qt
AIrFoFodFo
H
t
¥
-*
=
¥¥
==
¥
**
=
éù
m
=mm-m+
êú
l
ëû
éù
ttt
êú
+-m=-m+
êú
lll
ëû
+m-mmm
l
å
ò
åå
å
ò
(144)
Таким образом, подставив выражения (138) и (144) в выражение (137),
представим решение краевой задачи теплопроводности для цилиндра с
учетом теплопереноса в виде:
( )
( )
( ) ( ) ( )
0
0
0
1
,
,1,,.
nnn
c
n
trt
TrFoqLuFoAIrqFo
tt
¥
=
t-
==--mym
-
å
(145)
Здесь функция
(
)
,,
n
qFo
ym
представляется так:
( )
( )
( )
( )
22
0
2
,,1exp
exp.
Fo
nnn
n
qFoqLuFoFodFo
FoqLuFo
***
éù
êú
ym=+mm´
êú
êú
ëû
´-m-
ò
(146)
В последнем выражении поток влаги с поверхности цилиндра
определяется следующим образом:
( ) ( )
(
)
( )
0
.
m
c
q
qLuFoqFo
tt
t
==
a-
(147)
Произведем анализ полученных решений аналогично тому, как это
выполнено в [5]. При интенсивном теплообмене цилиндра с окружающей
средой
(
)
Bi
®¥
по всей его боковой поверхности устанавливается
постоянная температура, равная температуре среды t
c
. Гидродинамические
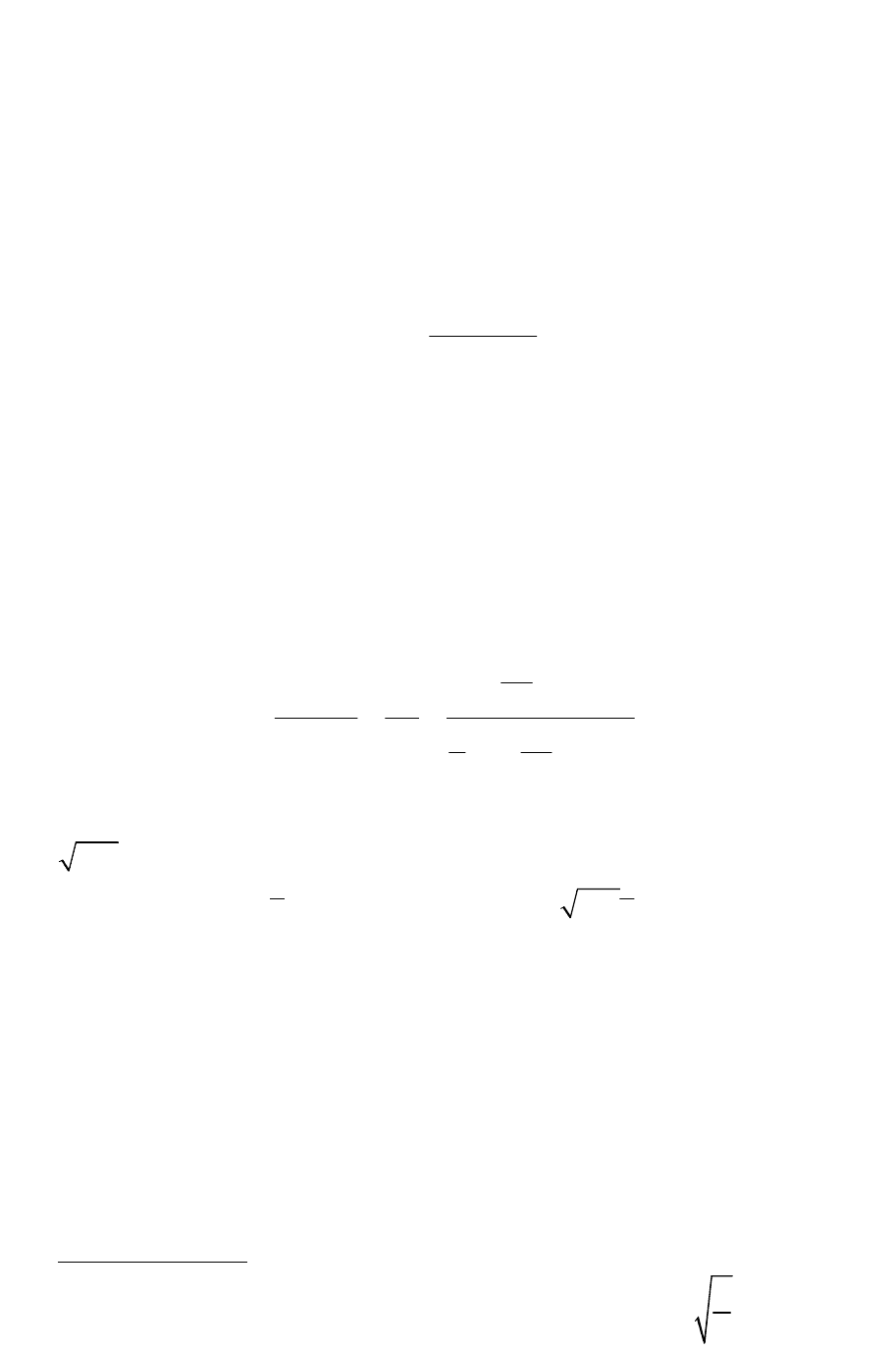
154
условия среды в этом случае перестают влиять на теплоперенос в
цилиндре. Изменение поля температур в нем определяется лишь
теплофизическими свойствами высушиваемого тела и интенсивностью
внешнего массообмена. При этом характеристическое уравнение (139)
принимает вид
(
)
0
0.
n
I
m=
Корни этого уравнения определяют нулевое
значение функции Бесселя первого рода нулевого порядка и могут быть
найдены с помощью таблиц [2-5].
Из выражения (139) следует, что в этом случае значения
коэффициента
n
A
будут определяться по формуле:
( )
1
2
.
n
nn
A
I
=
mm
(148)
В случае малой интенсивности внешнего теплообмена
(
)
0
Bi
®
из
характеристического уравнения следует, что
(
)
1
0.
n
I
m®
При этом, как
показано в [6], все коэффициенты
n
A
стремятся к нулю, за исключением
коэффициента
1
,
A
который принимает значение, равное единице.
Наиболее значимым является только первый корень характеристического
уравнения. Этот корень можно получить, разложив функции Бесселя в
степенной ряд в окрестности точки
( )
( )
2
1
2
0
3
1
11
2
1
1
2
.
11
2
2
n
n
n
I
IBi
-m+
m
m
==
m
m-m+
K
K
(149)
Ограничившись только первыми членами разложения, получим
1
2.
Bi
m= С учетом этого выражение (145) принимает следующий вид:
( ) ( )
(
)
0
,12,
TrFoqLuFoIBir
=--y
(150)
где функция y определяется так:
( ) ( )
( ) ( )
0
12exp2exp2.
Fo
BiqLuFoBiFodFoBiFoqLuFo
***
éù
êú
y=+--
êú
êú
ëû
ò
(151)
Таким образом, при малой интенсивности внешнего теплообмена
теплоперенос внутри цилиндра во многом определяется интенсивностью
внешней массоотдачи, т.е. скоростью отвода влаги с поверхности
цилиндра в окружающую среду.
Второй случай:
0,1;
m
Fo
<
0,1
Fo
<
. В условиях, когда и массо- и
теплообменные числа Фурье не превышают 0,1, величина
s
R
a
стремится к
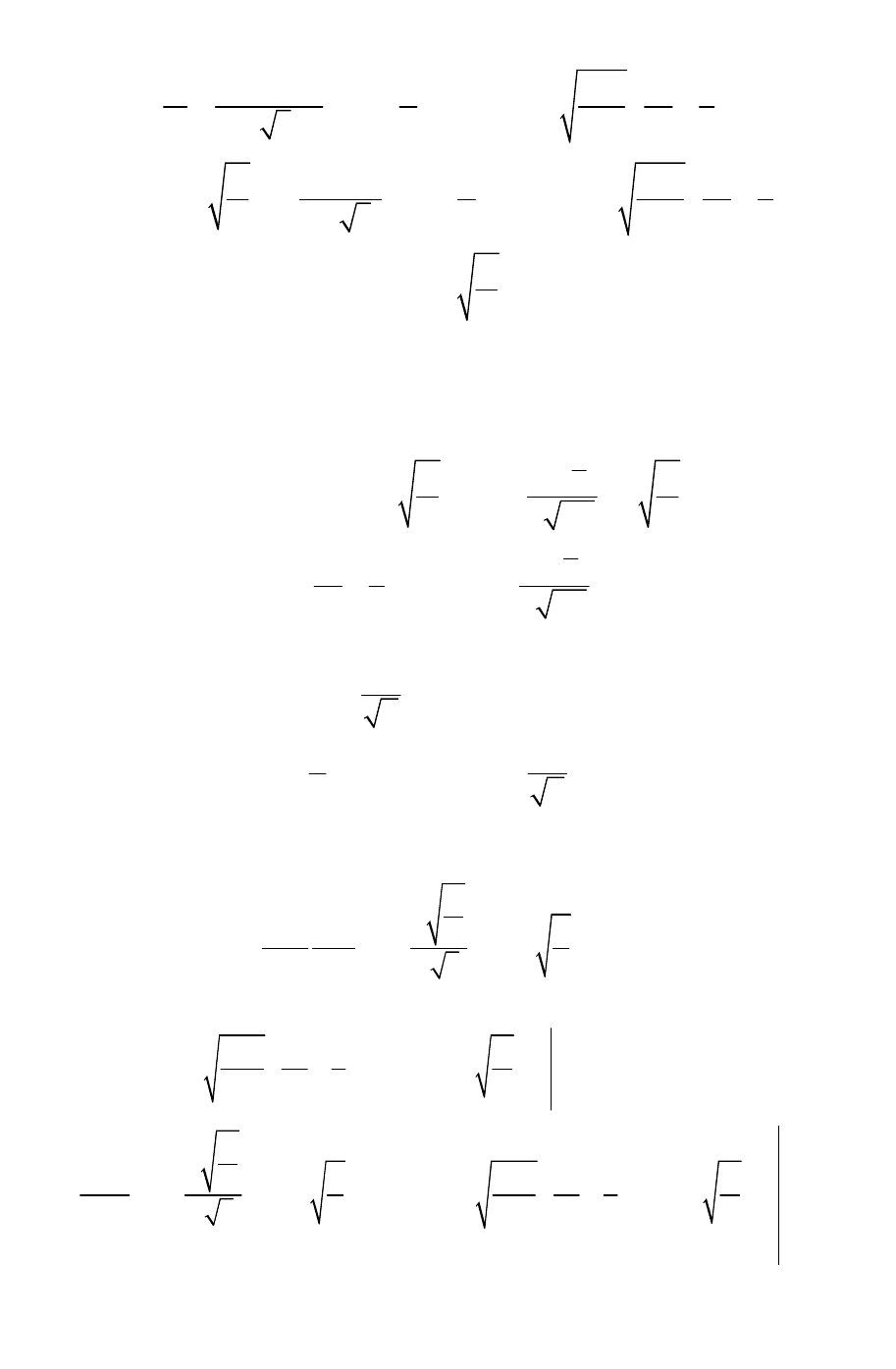
155
бесконечно большой величине. В этом случае функции Бесселя могут быть
разложены в асимптотический ряд. Выражение (136) преобразуем к виду:
( )
(
)
( )
)
()
( )
)
0
0
2
2
3
,exp1
88
3
exp1
88
.
c
tta
tsaR
trsRr
sar
ss
sR
sqsa
RsaR
HRHRr
rar
ss
sR
R
HRH
r
é
-
éùæ
-=--++-
ê
ç
êú
ëûè
ë
é
éùæ
-+----++-
ù
ê
ç
û
êú
a
ëûè
ë
-+
ù
û
K
K
(152)
Первое слагаемое в правой части выражения (152), как и ранее,
переводится из области изображений в оригиналы с помощью таблиц
обратных преобразований. Поэтому, не останавливаясь на подробностях,
приведем окончательный результат:
{} ( )
1
0
2
1
~24
2
31
.
88
2
ci
RrR
LttBiFoierfcBiFo
rr
Fo
Rr
Biierfc
r
Fo
-
ì
-
ï
=-+´
í
ï
î
-ü
æö
´+-
ý
ç÷
èø
þ
(153)
В выражении (153) приняты следующие обозначения:
(
)
()
2
1
exp;
ierfcxxxerfcx
=--
p
(154)
(
)
(
)
222
12
12exp.
4
ierfcxerfcxx
éù
=+--
êú
p
ëû
(155)
Для возвращения в область оригиналов второго слагаемого правой части
выражения (152) применим вновь теорему Дюамеля:
()
( )
()
( )
2
11
0
2
1
2
0
~exp
3
1
88
3
exp1.
88
Fo
t
R
a
qt
s
r
LLRr
Foa
ss
aRR
HRHdFo
rr
sR
R
a
q
saRR
r
LRrHRH
arr
ss
sR
--
*
t-
-
t=
ì
ï
éù
éù
¶
ï
=--´
í
êú
êú
a¶
ëû
ëû ï
ï
î
ü
éù
ï
æö
´++-++
ý
êú
ç÷
èø
ï
ëû
þ
ìü
ïï
éùéù
t
ïï
æö
+---+-
íý
êúêú
ç÷
a
èø
ëûëû
ïï
ïï
îþ
ò
K
(156)
Из (153) непосредственно следует, что при
0
Fo
=
(т.е. при t = 0) оно
принимает значение, равное нулю. Следовательно, последнее слагаемое в
(156) также равно нулю. Обратное преобразование Лапласа от выражения,
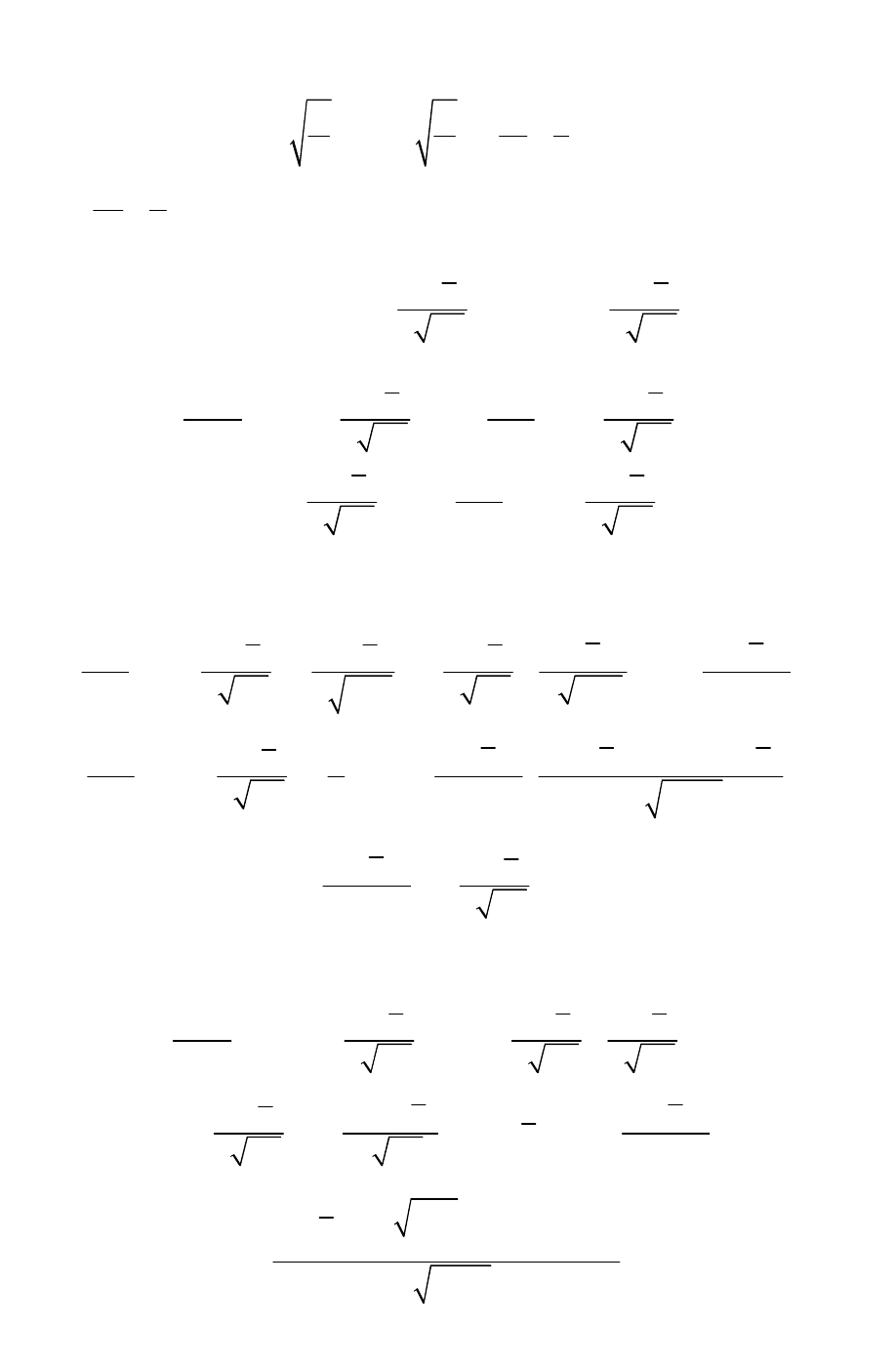
156
стоящего в круглых скобках (156), имеет вид зависимости, находящейся в
фигурных скобках (153). Прежде чем выполнить дифференцирование
этого выражения по Fo, примем следующие обозначения:
3
2;42,
88
RRR
PBiQBiBiPl
rrr
æö
==+-=
ç÷
èø
(157)
где:
3
2.
44
R
lBi
r
=+- (158)
В этом случае фигурная скобка (153) преобразуется к виду:
{}
2
11
~.
22
rr
PFoierfcQFoierfc
FoFo
--
=+ (159)
Дифференцируя по Fo, получаем:
{
}
22
~
11
22
11
.
22
rr
PierfcPFoierfc
FoFo
FoFo
rr
QierfcQFoierfc
Fo
FoFo
¶
-¶-
æö
=++
ç÷
¶¶
èø
-¶-
æö
++
ç÷
¶
èø
(160)
Выполняя дифференцирование функционалов от интеграла ошибок,
имеем:
( ) ( )
22
3
11
111
exp
4
224
2
rr
rrr
ierfcerfc
FoFo
FoFoFo
Fo
éù
--
¶---
æö
êú
=--
ç÷
¶
p
êú
èø
ëû
(161)
( ) ( ) ( )
( )
23
2
3
2
2
13121
11
exp
44
2
2
1
1
.
2
rrFor
r
ierfc
FoFo
Fo
FoFo
r
r
erfc
Fo
Fo
ì
éù
----
¶-
æö
ï
êú
=--
í
ç÷
¶
êú
èø
ï
p
ëû
î
ü
-
-
ï
-
ý
ï
þ
(162)
Подставив выражения (161) и (162) в (160) и выполнив ряд
преобразований, запишем:
{
}
( )
( )
( )
( )
2
2
3
3
~
111
222
11
1
1exp
4
22
1232
.
8
rrr
QierfcPierfc
Fo
FoFoFo
Qrr
r
erfcPr
Fo
FoFo
rPFoQQFo
Fo
¶
---
=++´
¶
éù
--éù
-
êú
´-+--´
êú
êú
ëû
ëû
éù
æö
-+-
ç÷
êú
èø
´
êú
êú
p
êú
ëû
(163)
Осуществляя переход из области изображений в область оригиналов в
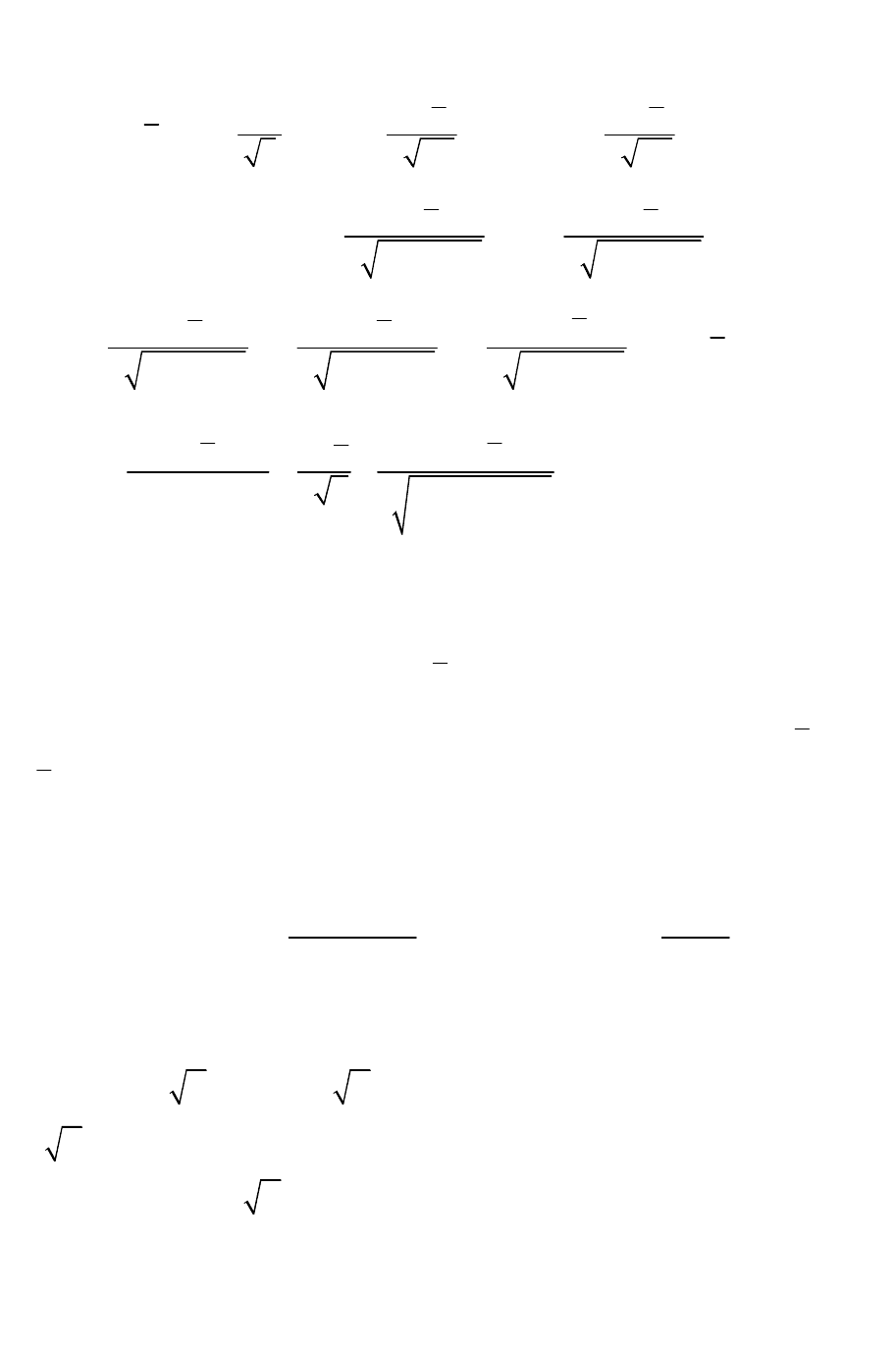
157
выражении (152) с учетом зависимостей (153), (156) и (163), после
преобразований окончательно получаем:
( )
( )
( )
( )
( )
( )
( )
( )
( )
2
2
0
2
211
,1
22
11
22
1
11
11
222
131
1
exp2
4
4
8
Fo
Birr
TrFoFoierfcFolierfc
rFoFo
rr
qLuFolierfcierfc
FoFoFoFo
lr
rr
erfcr
FoFoFoFoFoFo
rlr
r
FoFol
FoFo
FoFo
*
**
***
*
*
*
--
ì
=+-
í
î
ì
--
ï
-++
í
ï
--
î
éù
-
--
+-+-´
êú
êú
---
ëû
é
éù
--
-
êú
´-+--
êú
p
-
p-
êú
ëû
ò
.
dFo
*
ü
ù
ï
êú
ý
êú
ï
êú
ëû
þ
(164)
Таким образом, выражения (130) и (164) в совокупности описывают
динамику изменения полей влагосодержаний и температур в цилиндре в
процессе сушки при малом времени тепловой обработки материала.
Необходимо отметить, что при
0
r
=
безразмерные влагосодержание и
температура принимают значения, равные бесконечности. Однако по
условию задачи в силу физических представлений функции
(
)
,
UrFo
и
(
)
,
TrFo
ограничены и не могут быть бесконечно большими.
Влагосодержание на оси цилиндра может быть определено по формуле:
( )
(
)
0
0
0,
1
0,14exp.
4
mm
pm
uu
UFoBiFo
uuFo
t-æö
==--
ç÷
-
èø
(165)
Чтобы получить зависимость для расчета температуры на оси
цилиндра, преобразуем выражение (136), предварительно разложив
функции
(
)
0
IpR
и
(
)
1
IpR
в асимптотический ряд, а функцию
(
)
0
IpR
- в степенной. Такой путь представления функций обусловлен
тем, что аргумент
pR
бесселевых функций при малых значениях Fo
стремится к большой величине. Поэтому разложение в асимптотический
ряд позволяет ограничиться только первым членом ряда, поскольку он
является наиболее значимым по сравнению с остальными. Разложение
модифицированной функции Бесселя первого рода n-го порядка в

158
асимптотический ряд имеет вид:
()
(
)
(
)
( )
2222
22
3
0
2
4143
141
1.
1!8
2
2!8
Izl
z
z
z
æö
n-n-
n
ç÷
=-+-
ç÷
p
ç÷
èø
K
(166)
В соответствии с этим для функций нулевого и первого порядка
получаем:
( )
( )
0
2
119
1;
8
2
128
pR
IpRl
pR
pR
pR
æö
ç÷
=+++
ç÷
p
ç÷
èø
K
(167)
( )
( )
1
2
1315
1.
8
2
128
pR
IpRl
pR
pR
pR
æö
ç÷
=---
ç÷
p
ç÷
èø
K
(168)
Отсюда при pR
®¥
следует:
(
)
(
)
01
11
;.
22
pRpR
IpReIpRe
pRpR
»»
pp
(169)
Разложение функции
(
)
0
Ipr
в степенной ряд имеет вид:
( ) ( )
4
2
0
22
111
1,
2
22
Iprprpr
æö
=-+
ç÷
èø
K
(170)
отсюда, в частности, имеем:
(
)
0
0
1.
lim
r
Ipr
®
=
(171)
Подставляя (169) и (171) в выражение (136), получаем:
( )
( )
(
)
()
( )
0
0
2exp
,
1
2exp
.
1
c
ttpRpR
t
trs
P
s
s
H
sqspRpR
p
s
H
-p-
-=-
æö
+
ç÷
èø
p-
-
æö
a+
ç÷
ç÷
èø
(172)
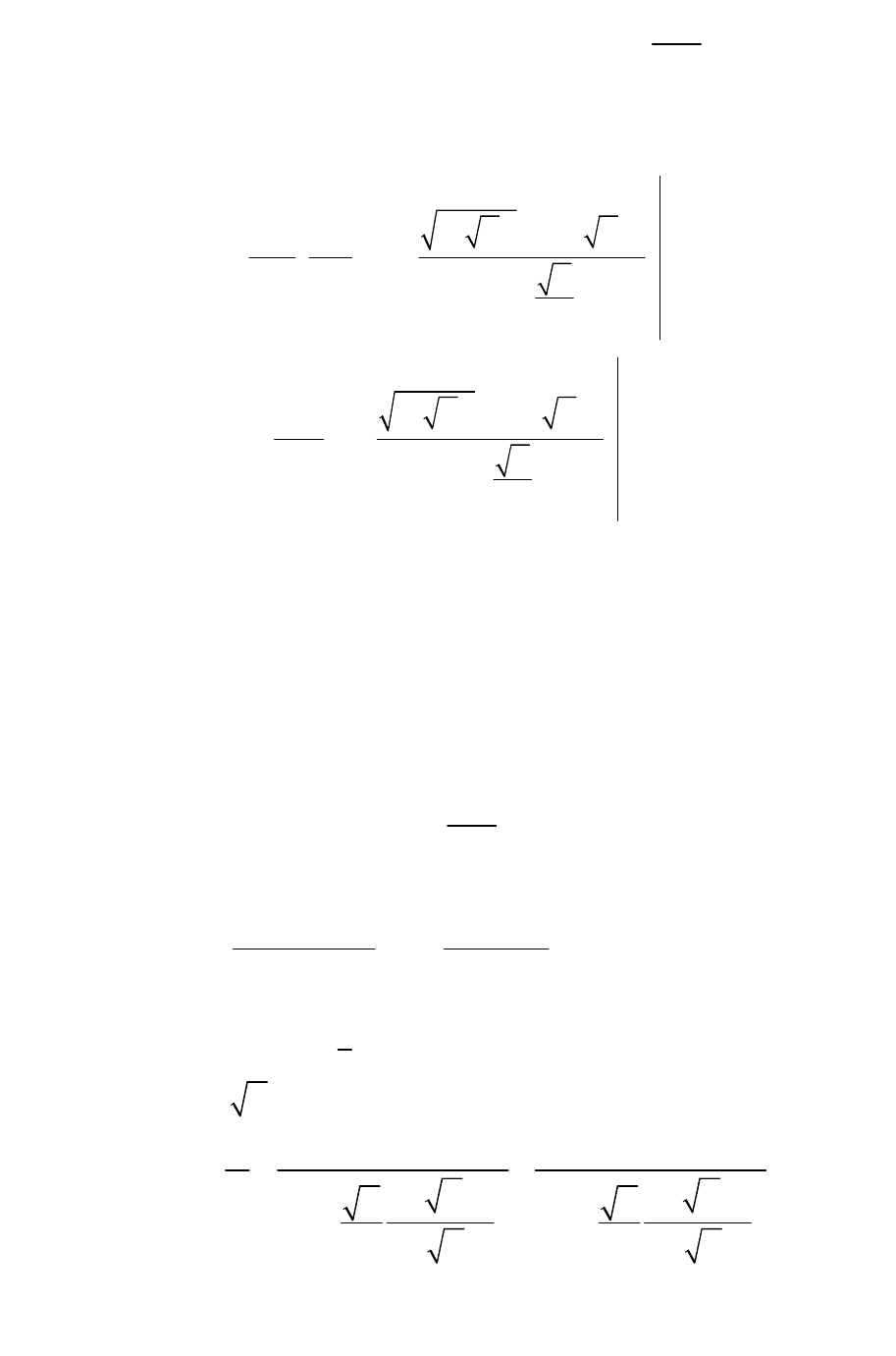
Осуществив переход из области изображений в область оригиналов,
для первого слагаемого правой части (172), запишем:
159
( ) ( )
1
1
00
1
~4exp.
4
cc
LttttBiFo
Fo
-
éù
æö
=----
êú
ç÷
èø
ëû
(173)
Второе слагаемое правой части (172) переведем в область оригиналов,
вновь применив теорему Дюамеля:
()
( )
()
( )
2
11
0
1
0
2exp
~
1
2exp
.
1
Fo
t
pRpR
qt
LLdFo
Fo
p
s
H
pRpR
q
L
p
s
H
--*
t-
-
t=
ìü
éù
ïï
êú
p-
ïï
éù
¶
ïï
êú
=×+
íý
êú
êú
a¶
æö
ëû
ïï
êú
+
ç÷
ç÷
ïï
êú
èø
ëû
ïï
îþ
éù
êú
p-
t
êú
+
êú
a
æö
êú
+
ç÷
ç÷
êú
èø
ëû
ò
(174)
Анализируя выражение (173), можно отметить, что при Fo=0 второе
слагаемое в нем обращается в нуль. Следовательно, обратное
преобразование от квадратной скобки, стоящей во втором слагаемом (174),
при t=0 принимает значение, равное единице. Выполнив
дифференцирование под знаком интеграла и сделав соответствующие
преобразования, окончательное выражение для определения температуры
на оси цилиндра запишем в виде:
( )
( )
( )
( )
0
1
0,14exp
4
11
exp4.
4
Fo
TFoBiFoBiqLuFo
Fo
dFoqLuFo
FoFo
FoFo
*
*
*
*
æö
=--+´
ç÷
èø
éù
æö
êú
´---
ç÷
êú
-
èø
-
êú
ëû
ò
(175)
Для определения температуры на поверхности цилиндра преобразуем
уравнение (136), полагая
1.
r
=
В этом случае, поделив числитель и
знаменатель на
(
)
0
,
IpR
можно записать, что:
( )
(
)
( )
( )
(
)
( )
( )
0
0
11
00
,.
11
c
ttsqs
t
tRs
s
IpRIpR
pp
ss
HH
IpRIpR
-
-=-
éùéù
êúêú
++
êúêú
ëûëû
(176)
Принимая во внимание выражения (167)–(168), для отношения
бесселевых функций получим:

160
( )
( )
( )
2
1
1
315
1
8
128
1
1.
19
2
1
128
8
pR
IpRpR
pl
IpR
pR
---
=»-
+++
K
K
(177)
При этом выражение (176) принимает следующий вид:
( )
(
)
(
)
0
0
,.
11
11
22
c
ttsqs
t
tRs
s
pp
ss
HHRHHR
-
-=-
æöæö
+-a+-
ç÷ç÷
ç÷ç÷
èøèø
(178)
Осуществляя по изложенной ранее процедуре переход от изображения
функции к оригиналу с использованием теоремы Дюамеля, окончательно
будем иметь:
( ) ( ) ( )
{ }
( )
( )
( )
( )
{
( )
2
0
2
1,1exp0,50,5
0,5
exp0,50,50,5
Fo
Bi
TFoBierfcBiFoBiqLuFo
Bi
BiFoFoBierfcBiFoFo
*
**
éù
=---+´
éù
ëû
êú
ëû
-
éù
éù
´-----+
êú
êú
ëû
ëû
ò
()
()
()
2
1
exp0,5.
BiFoFodFo
FoFo
**
*
ü
ï
éù
+---
ý
êú
ëû
ï
p-
þ
(179)
Легко видеть, что при отсутствии потока влаги с поверхности
цилиндра (т.е. при отсутствии сушки), выражения (175) и (179) переходят в
классические решения задачи теплопроводности для неограниченного
цилиндра, достаточно хорошо исследованные в монографии А.В. Лыкова
[5].
Обобщенные выражения для определения полей влагосодержаний
и температур высушиваемого материала
Анализируя выражения (60), (72) и (131), определяющие величину
потока влаги с поверхности пластины, цилиндра и сферы, замечаем, что
все эти зависимости могут быть представлены одной формулой вида
( )
(
)
( )
( )
{
( )
}
0
2
0
1exp0,5
0,5
0,51,
p
m
m
cm
m
pruu
Bi
qLuFoLuFoBi Г
ttBi Г
erfcBi Г LuFo
*
b-
é
éù
=--´
ê
êú
ëû
a--
ë
ù
éù
´--
ú
ëû
û
(180)
