Левшунов В.М Инженерные конструкции
Подождите немного. Документ загружается.

51
3.3. Методика статических расчетов
Для выполнения статических расчетов осуществляется переход
от абсолютных размеров полосы загружения к приведенным разме-
рам. Приведенные размеры устанавливаются в долях от полуширины
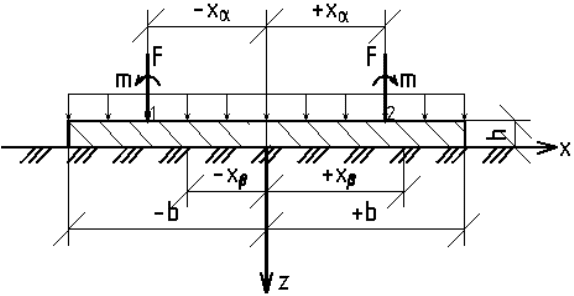
полосы загружения. Основными из них являются (рис. 13):
– ±х
α
= ±х/b – приведенная абсцисса нагруженного поперечного
сечения;
– ±х
β
= ±х/b – приведенная абсцисса расчетного поперечного се-
чения.
Рис. 13. Расчетная схема симметричной
нагрузки для полосы загружения конечной длины
Статический расчет заключается в том, чтобы установить орди-
наты эпюры контактных напряжений, поперечной силы и изгибаю-
щего момента.
Расчеты ординат эпюры контактных напряжений, поперечной
силы и изгибающего момента выполняются для поперечных сечений
справа и слева от середины полосы загружения с абсциссами через
каждые 0.1b. Интерполяция абсцисс поперечных сечений не допуска-
ется, так как может привести к грубым ошибкам.
При выполнении расчетов используется принцип Сен-Венана, ко-
торый заключается в том, что напряженное и деформируемое состоя-
ние не претерпевает заметных изменений, если нагрузка, приложен-
ная к некоторой части полосы загружения, заменяется статически эк-
вивалентной нагрузкой.
Ординаты эпюры контактных напряжений, поперечной силы и
изгибающего момента устанавливаются в зависимости от единичных
значений ординат.
При этом применяется следующее правило знаков.
52
Контактные напряжения считаются положительными, если ре-
активное давление упругого полупространства действует на полосу
загружения снизу вверх.
Поперечная сила считается положительной, если она направлена
вверх (стремится поднять часть полосы загружения, находящуюся
слева от расчетного сечения).
Изгибающий момент считается положительным, если он стре-
мится изогнуть полосу загружения выпуклостью вниз (растягиваются
крайние нижние волокна поперечного сечения).
Примечание. Контактные напряжения у краев полосы загружения не уста-
навливаются, так как упругое полупространство из-за пластических деформа-
ций не может оказывать заметного реактивного давления.
3.4. Общий порядок статических расчетов
для случая симметричной нагрузки
Симметричность нагрузки предполагает равную удаленность от
середины полосы загружения сосредоточенной силовой и моментной
нагрузки и равномерность распределенной нагрузки по полосе загру-
жения.
Общий порядок статических расчетов имеет следующую после-
довательность.
1. Устанавливается показатель гибкости К
λ
, расчетные значения
которого округляются до ближайшего целого числа, а именно 0, 1, 2,
3, 5, 7, 10, и определяется расчетная категория полосы загружения
конечной длины.
Примечание. Более подробная интерполяция существенной точности в ре-
зультаты расчетов не приносит.
2. Составляются расчетные зависимости В.А. Флорина для орди-
нат эпюры контактных напряжений, поперечной силы и изгибающего
момента.
3. Выполняется расчет ординат эпюры контактных напряжений,
поперечной силы и изгибающего момента для поперечных сечений
справа от середины полосы загружения.
Расчетные зависимости В.А. Флорина для ординат эпюры кон-
тактных напряжений, поперечной силы и изгибающего момента оп-
53
ределяются расчетными случаями симметричной нагрузки, воспри-
нимаемой полосой загружения конечной длины.
Сосредоточенная силовая нагрузка F
1. Контактные напряжения σ =σ
о
F/b, где σ
о
– единичное значение
ординат эпюры контактных напряжений (табл. 16, 18, 19, 22, 25, 28,
31, 34 [16]).
2. Поперечная сила Q = ±Q
o
F, где Q
o
– единичные значения ор-
динат эпюры поперечной силы (табл. 16, 18, 20, 23, 26, 29, 32, 35
[16]).
3. Изгибающий момент М = М
о
Fb, где М
о
– единичные значения
ординат эпюры изгибающего момента (табл. 17, 21, 24, 27, 30, 33, 36
[16]).
Сосредоточенная моментная нагрузка m
1 Контактные напряжения σ = σ
о
m/b
2
, где σ
о
– единичные значе-
ния ординат эпюры контактных напряжений (табл. 37, 40, 43, 46, 49,
52 [16]).
2. Поперечная сила Q = ±Q
o
m, где Q
o
– единичные значения ор-
динат эпюры поперечной силы (табл. 38, 41, 44, 47, 50, 53 [16]).
3. Изгибающий момент М = М
о
m, где М
о
– единичные значения
ординат эпюры изгибающего момента (табл. 39, 42, 45, 48, 51, 54
[16]).
Равномерно распределенная нагрузка q
1. Контактные напряжения σ = σ
о
q, где σ
о
– единичные значения
ординат эпюры контактных напряжений (табл. 18, 55).
2. Поперечная сила Q = ±Q
o
qb, где Q
o
– единичные значения ор-
динат эпюры поперечной силы (табл. 18, 56 [16]).
3. Изгибающий момент М = М
о
qb
2
, где М
о
– единичные значения
ординат эпюры изгибающего момента (табл. 18, 57 [16]).
В расчетных зависимостях В.А. Флорина знак плюс (+) при Q
o
для
расчетных поперечных сечений справа от середины полосы загруже-
ния, знак минус (–) – для расчетных поперечных сечений слева от се-
редины полосы загружения.
Для расчетных поперечных сечений жесткой полосы загружения
при х
β
≥ х
α
и для расчетных поперечных сечений короткой полосы за-
гружения при х
β
= х
α
единичные значения ординат Q
o
справа от точки
приложения сосредоточенной силовой нагрузки F исправляются на
величину «+Q
o
– 1», а единичные значения ординат М
о
справа от точ-
ки приложения сосредоточенной моментной нагрузки m исправляют-
54
ся на величину «–М
о
+ 1». При этом сосредоточенная моментная на-
грузка m считается положительной, если в правой половине полосы
загружения создает вращение по часовой стрелке, а в левой половине
полосы загружения – против хода часовой стрелки.
Примечания: 1. Если сосредоточенная силовая нагрузка F приложена в се-
редине полосы загружения (х
β
= 0), ордината эпюры поперечной силы Q в рас-
четном поперечном сечении при х
α
= 0 удваивается.
2. Если сосредоточенная моментная нагрузка m приложена в середине по-
лосы загружения (х
β
= 0), ордината эпюры изгибающего момента М в расчет-
ном поперечном сечении при х
α
= 0 взаимно уничтожается.
3. Жесткая полоса загружения конечной длины (К
λ
= 0), нагруженная со-
средоточенной моментной нагрузкой, не испытывает реактивного давления уп-
ругого основания.
3.5. Пример инженерного расчета
Пример 1. Установить расчетную толщину железобетонной пли-
ты днища резервуара чистой воды (РЧВ) из монолитного железобето-
на и выполнить статический расчет и расчеты на прочность попереч-
ного сечения. Плита опирается на влажный суглинок (Е
о
= 17 МПа).
Класс тяжелого бетона В20 (γ
b2
R
b
= 10.4 МПа, Е
п
= 26.5∙10
3
МПа).
Класс стержневой арматуры А400 (R
s
= 355 МПа).
Расчеты.
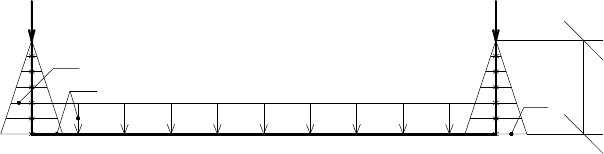
1. Расчетные нагрузки на один погонный метр плиты днища РЧВ
(рис. 14).
F F
h =z
qa
qw
qa
w
Рис. 14. Расчетные нагрузки на один погонный метр плиты днища РЧВ
1) Весовая масса воды q
w
= h
w
γ
w
γ
н
= 3.6∙(1.0∙10)∙1.0 = 36 кН/м
2
.
2. Весовая масса стеновой панели и плиты покрытия F = (Q
ст
/L +
Q
п
/2Н)1.1 = (48/2.98 + 15/2∙1.48)∙1.1= 23.3 кН.
3) Изгибающий момент гидростатического давления столба воды
на стеновую панель высотой 3.6 м m
w
= [(0.5q
w
h
w
)∙(0.333h
w
)]γн =
55
0.17h
w
3
γ
w
γ
н
= 0.17∙3.6
3
(1.0∙10)∙1.0 = 79.3 кНм (по ходу часовой стрел-
ки справа и против хода часовой стрелки слева).
4) Изгибающий момент активного давления грунта на стеновую
панель высотой 3.6 м m
a
= (0.5q
a
z
)
∙(0.333z)γ
н
= 0.17z
3
γ
a
γ
н
=
0.7∙3.6
3
∙0.26∙1.2 = 44.5 кНм (против хода часовой стрелки справа и по
ходу часовой стрелки слева).
5) Расчетный изгибающий момент m = m
w
– m
a
= 79.3 – 44.5 =
34.8 кНм (по ходу часовой стрелки справа и против хода часовой
стрелки слева).
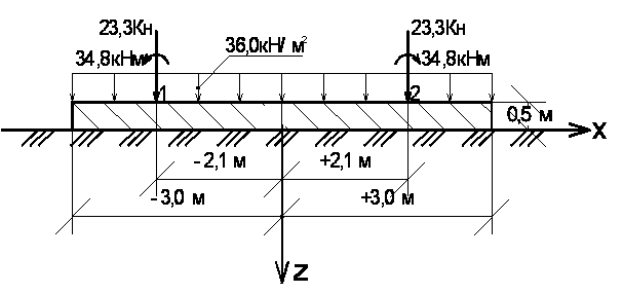
2. Расчетная схема нагружения полосы загружения плиты днища
РЧВ (рис. 15).
Рис. 15. Расчетная схема нагружения полосы
загружения плиты днища РЧВ
3. Расчетная толщина полосы загружения.
1) Ординаты эпюры контактных напряжений в крайних точках
полосы загружения (рис. 12) σ
А
= σ
В
= q
w
+ ΣF/2b = 36.0 +(23.3 +
23.3)∙(2∙3) = 43.8 кН/м
2
.
2) Изгибающий момент в расчетном поперечном сечении полосы
загружения.
M
1
= (σ
A
– q)a
1
2
/2
– m = (43.8 – 36.0)∙0.9
2
/2 = –31.6 кНм.
M
2
= (σ
A
– q)a
2
2
/2 – m – F(a
2
– a
1
) + m = (43.8 – 36.3)∙5.1
2
/2 – 34.8 –
23.3(5.1 – 0.9) + 34.8 = 2.92 кНм.
3) Рабочая толщина (без учета защитного слоя бетона) полосы за-
гружения при расчетном изгибающем моменте М
р
– 31.6 кНм и опти-
мальном проценте армирования μ
опт
= 0.29…0.43% (табл. 15 [16]) h
o
=
γ
μ
[(γ
з
М
р
)/b
L
]
0.5
= μ
опт
(R
s
/γ
b2
R
b
)[(γ
з
М
р
)/b
L
]
0.5
.
Оптимальный процент армирования μ
опт
= 0.29% h
o
= (029/100) ∙
(355/10.4)∙[(1.8∙31.6∙10
5
)/100]
0.5
= 24.4 см.
56
Оптимальный процент армирования μ
опт
= 0.43% h
o
= (0.43/100) ∙
(355/10.4)∙[(1/8∙31.6)/100]
0.5
= 36.2 см.
Среднее арифметическое значение рабочей толщины полосы за-
гружения h
o
= (24.4 + 36.2)/2 = 30.3 см.
4) Толщина полосы загружения при защитном слое бетона а = 3 см,
h = h
o
+ a = 30.3 + 3 = 33.3 см, принимаем h = 35 см.
5) Показатель гибкости полосы загружения К
λ
= (Е
о
/Е
п
)(b
3
/h
3
)=
10∙(17/26.5∙10
3
)∙(3
3
/0.35
3
) = 3.96, принимаем К
λ
= 3.0.
6) Ординаты эпюры изгибающего момента в расчетном попереч-
ном сечении (х
β
= –2.1/3 = –0.7) короткой полосы загружения конеч-
ной длины на упругом основании, нагруженной симметрично относи-
тельно середины полосы сосредоточенной силовой F = 23.3 кН и мо-
ментной m = 34.8 кНм нагрузкой и равномерно распределенной на-
грузкой q = 36.0 кН/м
2
(х
α
= –2.1/3 = –0.7) M
1
= M
oF
Fb + M
om
m
+
M
oq
qb
2
= 0.08∙23.3∙3 + (–0.93)∙34.8 + 0.032∙36∙3
2
= –16.4 кНм (табл. 27,
45, 57 [16]).
7) Рабочая толщина короткой полосы загружения конечной дли-
ны на упругом основании при расчетном изгибающем моменте М
р
=
16.4 кНм.
Оптимальный процент армирования μ
опт
= 0.29% h
o
= (0.29/100) ∙
(355/10.4)∙[1.8∙(16.4∙10
5
)/100]
0.5
= 17.5 см.
Оптимальный процент армирования μ
опт
= 0.43% h
o
= (0.43/100) ∙
(355/10.4)∙[1.8∙(16.4∙10
5
)/100]
0.5
= 25.9 см.
Среднее арифметическое значение рабочей толщины короткой
полосы загружения конечной длины на упругом основании h
o
(17.5 +
25.8)/2 = 21.7 см.
8) Толщина короткой полосы загружения конечной длины на уп-
ругом основании при защитном слое бетона а = 3 см, h = 21.7 + 3 =
24.7 см, принимаем h = 25 см.
4. Статический расчет короткой полосы загружения конечной
длины на упругом основании, нагруженной симметрично относи-
тельно середины полосы сосредоточенной силовой F = 23.3 кН и мо-
ментной m = 34.8 кНм нагрузкой и равномерной распределенной на-
грузкой q = 36.0 кН/м
2
(рис. 15).
1) Показатель гибкости короткой полосы загружения конечной
длины на упругом основании К
λ
=10∙(17/26.5∙10
3
)∙(3
3
/0.25
3
) = 11.1,
принимаем К
λ
= 10.

57
2) Ординаты эпюры контактных напряжений, поперечной силы и
изгибающего момента для поперечных сечений справа от середины
короткой полосы загружения конечной длины на упругом основании
(расчетные табл. 4, 5, 6).
Расчетная зависимость для контактных напряжений σ = σ
oF
F/b +
σ
om
m/b
2
+ σ
oq
q = 7.8σ
oF
+ 3.9σ
om
+ 36.0σ
oq
(табл. 34, 52, 55 [16]).
Расчетная зависимость дл поперечной силы Q = Q
oF
F + Q
om
m/b +
Q
oq
qb = 23.3Q
oF
+ 11.6Q
om
+ 108Q
oq
(табл. 35, 53, 56 [16]).
Расчетная зависимость для изгибающего момента M = M
oF
Fb +
M
om
m + M
oq
qb
2
= 69.9M
oF
+ 34.8M
om
+ 324M
oq
(табл. 36, 54, 57 [16]).
Расчетная таблица 4
Ординаты эпюры контактных напряжений
для короткой полосы загружения конечной длины
на упругом основании при К
λ
= 10, кн/м
2
х
β
для поперечных сечений справа от середины полосы загружения, м Сим-
вол
0 0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3.0
σ
F
σ
m
σ
q
σ
4.2
–6.3
30.2
28.1
4.3
–6.2
30.2
28.3
4.5
–6.0
30.2
28.7
4.9
–5.6
30.2
29.1
5.5
–4.9
30.2
30.8
6.2
–3.8
30.6
33.0
7.3
–2.0
31.7
37.0
8.7
1.1
34.2
44.0
10.7
5.9
40.0
56.6
14.3
13.3
51.8
79.4
–
–
–
–
Примечание. Для поперечных сечений слева от середины полосы загруже-
ния ординаты эпюры такие же, как и для поперечных сечений справа от сере-
дины полосы загружения.
Расчетная таблица 5
Ординаты эпюры поперечной силы
для короткой полосы загружения конечной длины
на упругом основании при К
λ
= 10, кН
х
β
для поперечных сечений справа от середины полосы загружения, м Сим-
вол
0 0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3.0
Q
F
Q
m
Q
q
Q
0
0
0
0
1.2
–1.9
–1.7
–2.4
2.6
–3.7
–3.6
–4.7
4.0
–5.5
–5.3
–6.8
5.6
–7.0
–7.0
–8.4
7.2
–8.2
–8.6
–9.6
9.1
–9.1
–10
–10
11.6
–12
–9.4
–11
–9
–32
–8.9
–8.5
–11
–28
–5.1
–5.6
–5.4
–16
0
0
0
0
Примечание. Для поперечных сечений слева от середины полосы загруже-
ния ординаты эпюры такие же, как и для поперечных сечений справа от сере-
дины полосы загружения, но с обратным знаком.
58
Расчетная таблица 6
Ординаты эпюры изгибающего момента
для короткой полосы загружения конечной длины
на упругом основании при К
λ
= 10, кН/м
х
β
для поперечных сечений справа от середины полосы загружения, м Сим-
вол
0 0.3 0.6 0.9 1.2 1.5 1.8 2.1 2.4 2.7 3.0
M
F
M
m
M
q
M
–4.9
–17
20
–1.6
–4.2
–17
20
–1.5
–4.2
–18
19
–3.2
–2.8
–20
18
–4.5
–1.4
–21
16
–6.4
0.7
–24
13.6
–9.4
2.8
–26
11.0
–12
5.6
–29
5.9
7.8
–16
19.3
2.8
3.1
4.2
10.1
0.7
1.0
1.3
3.0
0
0
0
0
Примечание. Для поперечных сечений слева от середины полосы загруже-
ния ординаты эпюры такие же, как и для поперечных сечений справа от сере-
дины полосы загружения.
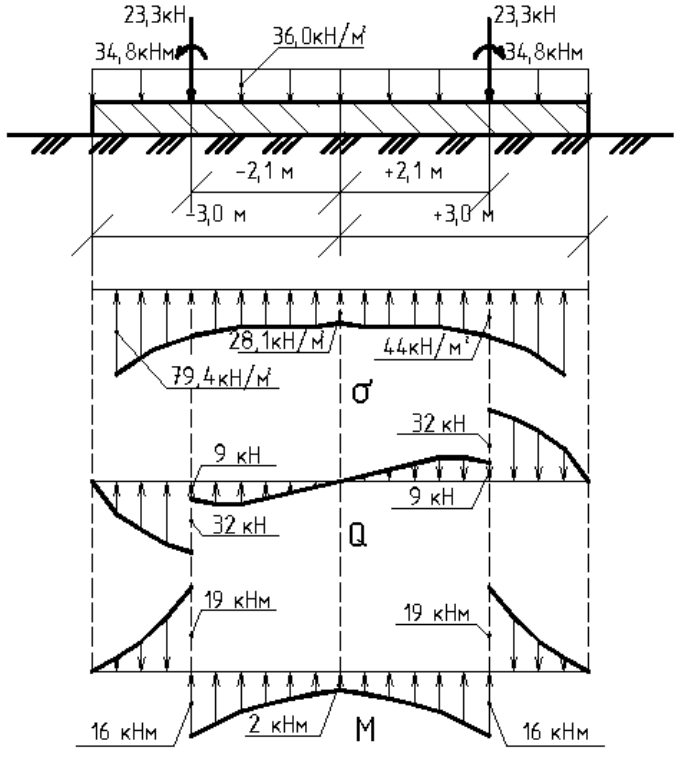
Расчетные эпюры контактных напряжений, поперечной силы и
изгибающего момента отражают общую закономерность напряжен-
ного и деформируемого состояния поперечных сечений плоской пли-
ты днища резервуара РЧВ (рис. 16).
Эпюра контактных напряжений имеет седловидную форму, сим-
метричную относительно середины полосы загружения. На концевых
участках плиты (левом и правом) значения ординат стремятся к бес-
конечности и в расчет не принимаются из-за пластических деформа-
ций, нарушающих упругие свойства основания. В нагруженном попе-
речном сечении возможен срез по наклонному к продольной оси се-
чению. Здесь контактные напряжения составляют 56% от расчетного
значения [(44/79)∙100%] и превышают величину контактных напря-
жений в середине плиты в 1.6 раза (44/28).
Эпюра поперечной силы показывает, что в центре плиты и на
концевых участках ординаты равны нулю. При этом правую часть
плиты поперечная сила стремится прижать к упругому основанию, а
левую часть – приподнять. Однако упругое основание подвергается
сжимающему действию по всей плите, так как ординаты эпюры кон-
тактных напряжений положительные, т.е. расчетное давление упруго-
го основания действует на плиту снизу вверх. В нагруженном попе-
речном сечении имеет место скачек на величину сосредоточенной
силовой нагрузки: F = 23.3 кН.
59
Рис. 16. Расчетные эпюры контактных напряжений, поперечной силы
и изгибающего момента для короткой полосы загружения конечной длины
на упругом основании при К
λ
= 10
Эпюра изгибающего момента характеризуется тем, что централь-
ная часть плиты между нагруженными поперечными сечениями де-
формируется выпуклостью вверх, вызывая осевое растяжение верх-
них волокон поперечного сечения и осевое сжатие нижних волокон.
Концевые участки плиты за нагруженными поперечными сечениями
деформируются выпуклостью вниз, вызывая осевое растяжение ниж-
них волокон поперечного сечения и осевое сжатие верхних волокон.
Примечание. Векторное направление ординат эпюры контактных напряже-
ний, поперечной силы и изгибающего момента соответствует принятому пра-
вилу знаков.
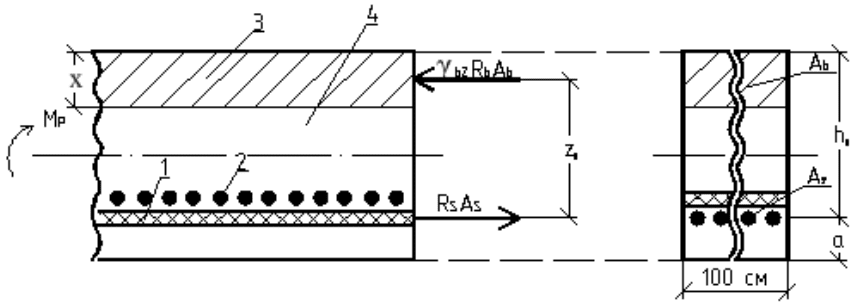
5. Расчеты на прочность нормального к продольной оси попереч-
ного сечения полосы загружения (рис. 17).
60
Рис. 17. Расчетная схема нормального
к продольной оси поперечного сечения полосы загружения:
(1 – продольные стержни арматурной сетки;
2 – поперечные стержни арматурной сетки; 3 – сжатая зона бетона;
4 – растянутая зона бетона)
1) Коэффициент влияния относительной высоты сжатой зоны бе-
тона на величину изгибающего момента, воспринимаемого сжатой
зоной бетона: К
b
= M
p
/(γ
b2
R
b
bh
o
2
) = (19.3∙10
5
)/[(10.4∙10
2
)∙100∙(25 – 3)
2
]
= 0.038.
2) Относительная высота сжатой зоны бетона ξ = 1 – (1 – 2К
b
)
0.5
=
= 1 – (1 – 2∙0.038)
0.5
= 0.039 < ξ
опт
= 0.1.
Понижаем класс бетона до В10 (γ
b2
R
b
= 5.4 МПа), увеличиваем
защитный слой бетона до а = 6 см и получаем: К
b
=(19.3∙10
5
)/[(5.4∙10
2
)
∙ 100∙(25 – 6)
2
] = 0.099; ξ = 1 –(1 – 2∙0.099)
0.5
= 0.104 < ξ
R
= 0.585.
3) Коэффициент влияния относительной высоты сжатой зоны бе-
тона на величину изгибающего момента, воспринимаемого арматурой
в растянутой зоне бетона: К
s
= (1 – 0.5ξ) = (1 – 0.5∙0.104) = 0.948 >
К
sR
= 0.707.
4) Требуемая площадь поперечного сечения арматуры в растяну-
той зоне бетона на один погонный метр A
s
≥ M
p
/(γ
s
h
o
R
s
) = (19.3∙10
5
)/
[0.948∙19∙(355∙10
2
)] = 2.94 см
2
/м.
5) Расчетный процент армирования μ = [А
s
/(bh
o
)]100% =
[2.94/(100∙19)]∙100% = 0.15% < μ
max
= 0.95%.
6) Расчетная высота сжатой зоны бетона x = (R
s
A
s
)/(γ
b2
R
b
b) =
[(355∙10
2
)∙2.94]/[(5.4∙10
2
)∙100] = 2.0 см.
7) Коэффициент влияния относительной высоты сжатой зоны бе-
тона на величину изгибающего момента, воспринимаемого арматурой
в растянутой зоне бетона: К
s
=1 – 0.5(х/h
o
) = 1 – 0.5∙(2.0/19) = 0.947.
