Левшин Г.Е. Управление техническими системами
Подождите немного. Документ загружается.

31
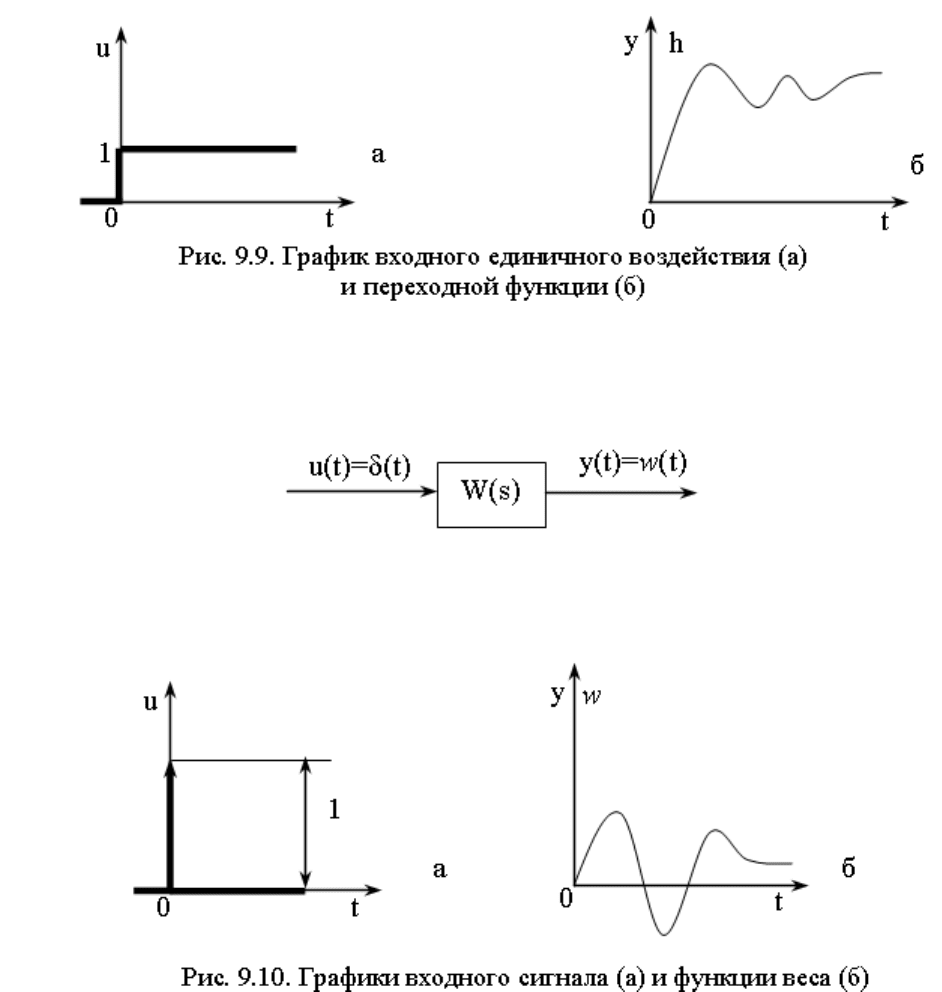
9.4.3. Функцией веса (или импульсной переходной функцией) звена
)(tw
называется его реакция на
входной сигнал в виде единичного импульса
)()( ttu
δ
=
при условии, что до приложения входного
воздействия звено находилось в покое. Здесь
)(t
δ
– так называемая дельта-функция (рис. 9.10).
Единичный импульс – это математическая идеализация предельно короткого импульсного сигнала.
Реально - это кратковременный удар на вал двигателя, ток короткого замыкания, отключение с АПВ
(автоматическим повторным включением, например, масляным выключателем) и др.
Временными характеристиками пользуются обычно при определении характера переходного процесса
в САР, когда входной сигнал не изменяется по гармоническому закону.
9.5. Частотные характеристики динамических звеньев
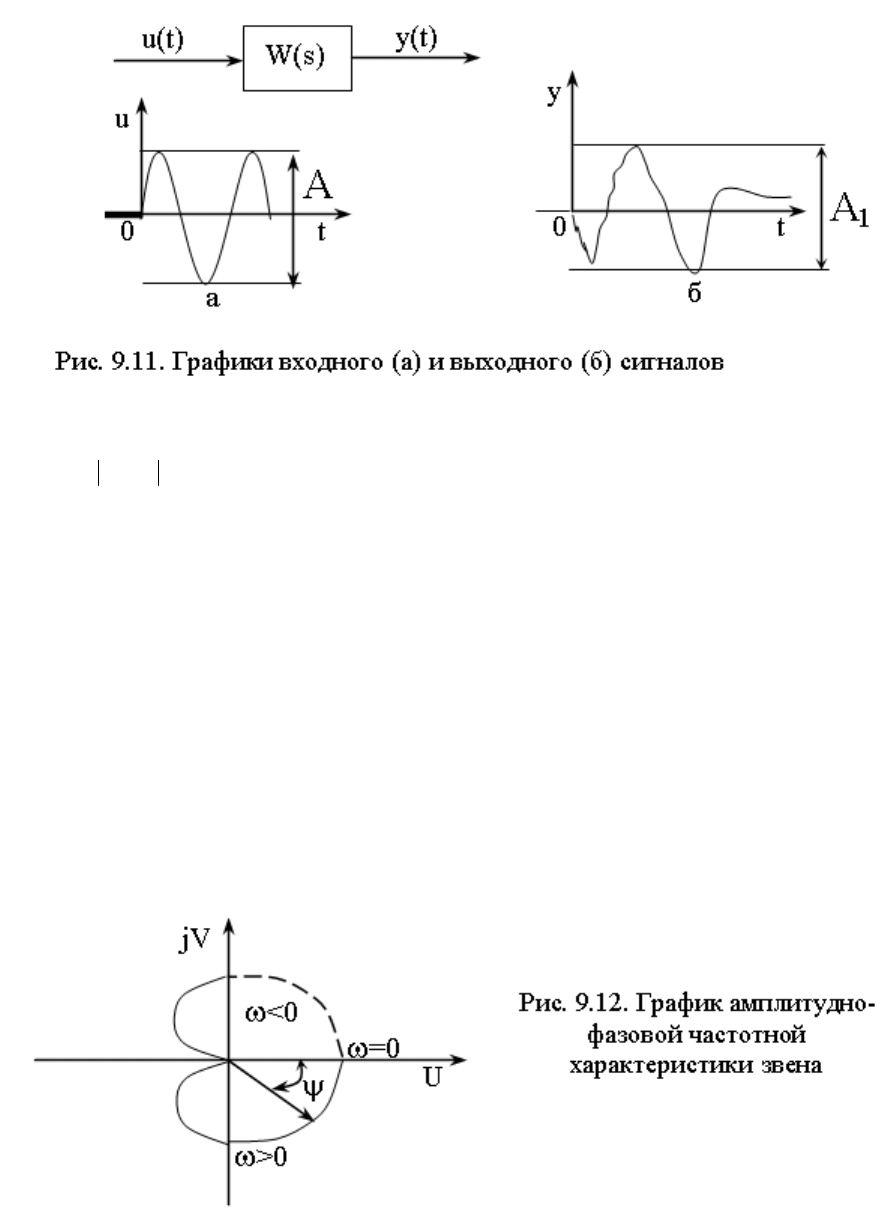
Если входной сигнал САУ изменяется по гармоническому закону заданной амплитуды и частоты, то
нахождение параметров колебаний на выходе САУ легче осуществлять с помощью частотных
характеристик. Пусть гармонический входной сигнал с амплитудой
A
и фазой
ϕ
проходит через
устойчивое звено. На выходе звена сигнал смещается по фазе и имеет другую амплитуду (рис. 9.11).
Искажённый вид начального участка выходного сигнала объясняется влиянием переходного процесса
32
Если в передаточной функции
)(sW
заменить
s
на
ω
j
)0(
∞
<
≤
ω
, то частотную передаточную
функцию звена можно представить в следующем виде:
)(
)()(
ωψ
ωω
j
eAjW =
,
где
)()(
ωω
jWA =
;
)(arg)(
ω
ω
ψ
jW=
.
Кроме того,
)()()(
ω
ω
ω
jVUjW +=
, где
)()(
ω
=
ω
jWRU
е
;
)()(
ω
ω
jimWV
=
.
Функция
)(
ω
A
называется амплитудной частотной характеристикой (а.ч.х.).
Функция
)(
ω
ψ
называется фазовой частотной характеристикой (ф.ч.х.) звена.
Функция
)(
ω
U
называется вещественной частотной характеристикой звена.
Функция
)(
ω
V
– мнимая частотная характеристика звена.
Для каждого фиксированного значения
i
ω
ω
=
частотная передаточная функция на плоскости
),( jVU
может быть изображена вектором
)(
i
A
ω
, отклонённым от положительного направления оси
абсцисс на угол
)(
i
ω
ψ
. Годограф этого вектора при изменении частоты от
0
до
+∞
называется амплитудно-
фазовой частотной характеристикой звена (рис. 9.12).
е
R
– действительная часть комплексного числа
)(
ω
jW
, (
reel
– действительный (франц.))
im
– мнимая часть комплексного числа
)(
ω
jW
, (
imaginaire
– мнимый (франц.))
arg
– аргумент комплексного числа
)(
ω
jW
, (это угол
ψ
, измеренный в радианах) – применяется при
тригонометрической форме записи комплексного числа.
9.6. Логарифмические частотные характеристики линейных звеньев
Частотные характеристики, построенные в логарифмических шкалах, называются логарифмическими
частотными характеристиками. При построении логарифмических характеристик на шкале частот,
например, вместо
ω
откладывают
ω
lg
. Это существенно упрощает исследование линейных САУ.
9.7. Типовые динамические звенья и их характеристики
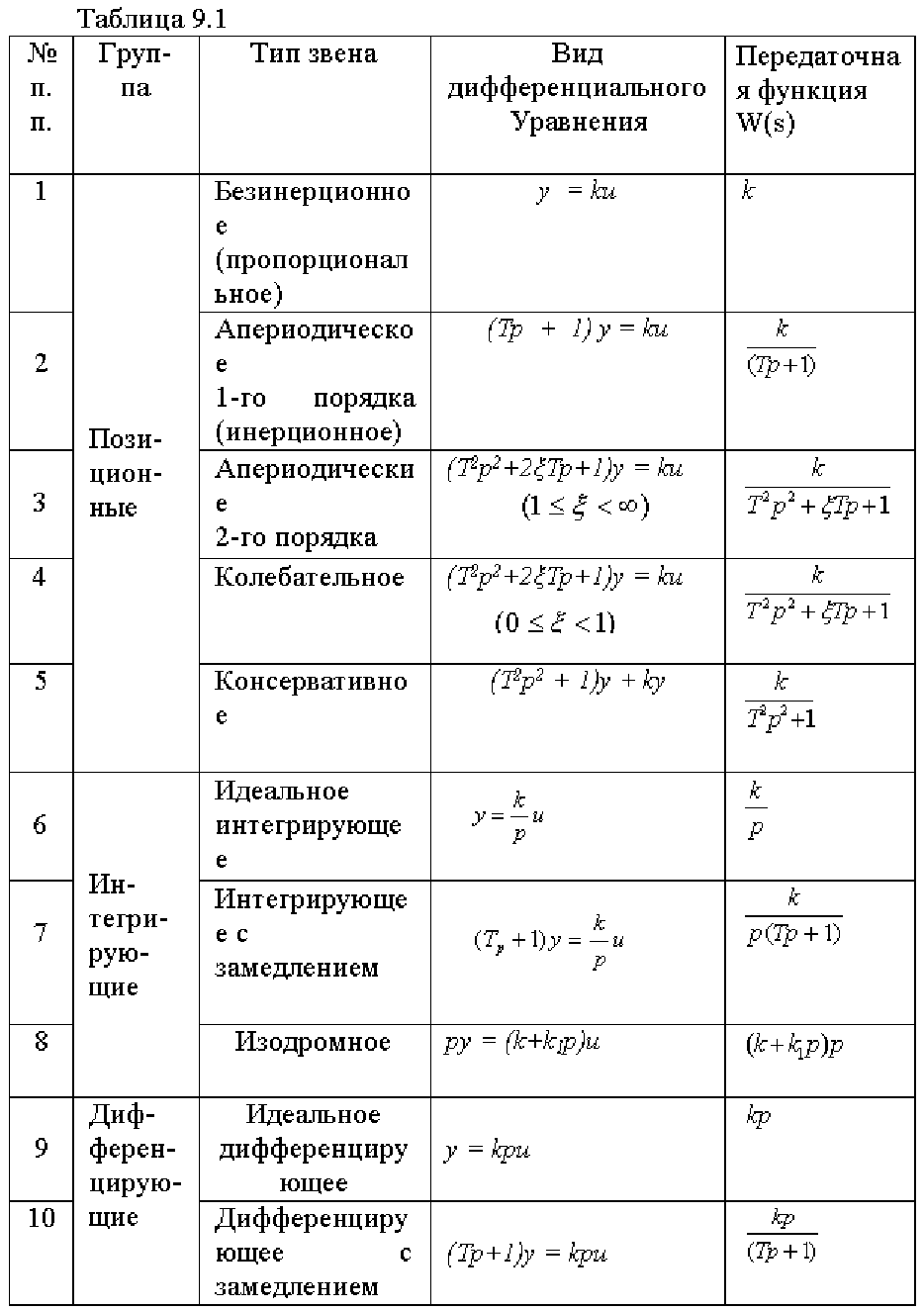
Типовыми динамическими звеньями называются звенья, описываемые дифференциальным уравнением
не выше второго порядка (в переменных вход и выход). Эти звенья классифицируют в зависимости от вида
33
левой и правой частей их дифференциального уравнения. Все типовые звенья разделяют на три группы:
позиционные, интегрирующие и дифференцирующие. Каждая из групп содержит несколько типовых
звеньев (табл. 9.1). К сожалению названия звеньев и их количество пока не одинаковы у разных авторов .
34
Примечание:
T
– постоянная времени, [с];
k
– коэффициент передачи звена;
ξ
– коэффициент
относительного демпфирования;
dtdp =
– символ дифференцирования, равнозначный записи
dtdy
или
dtdu
;
1
k
– передаточный коэффициент.
kp
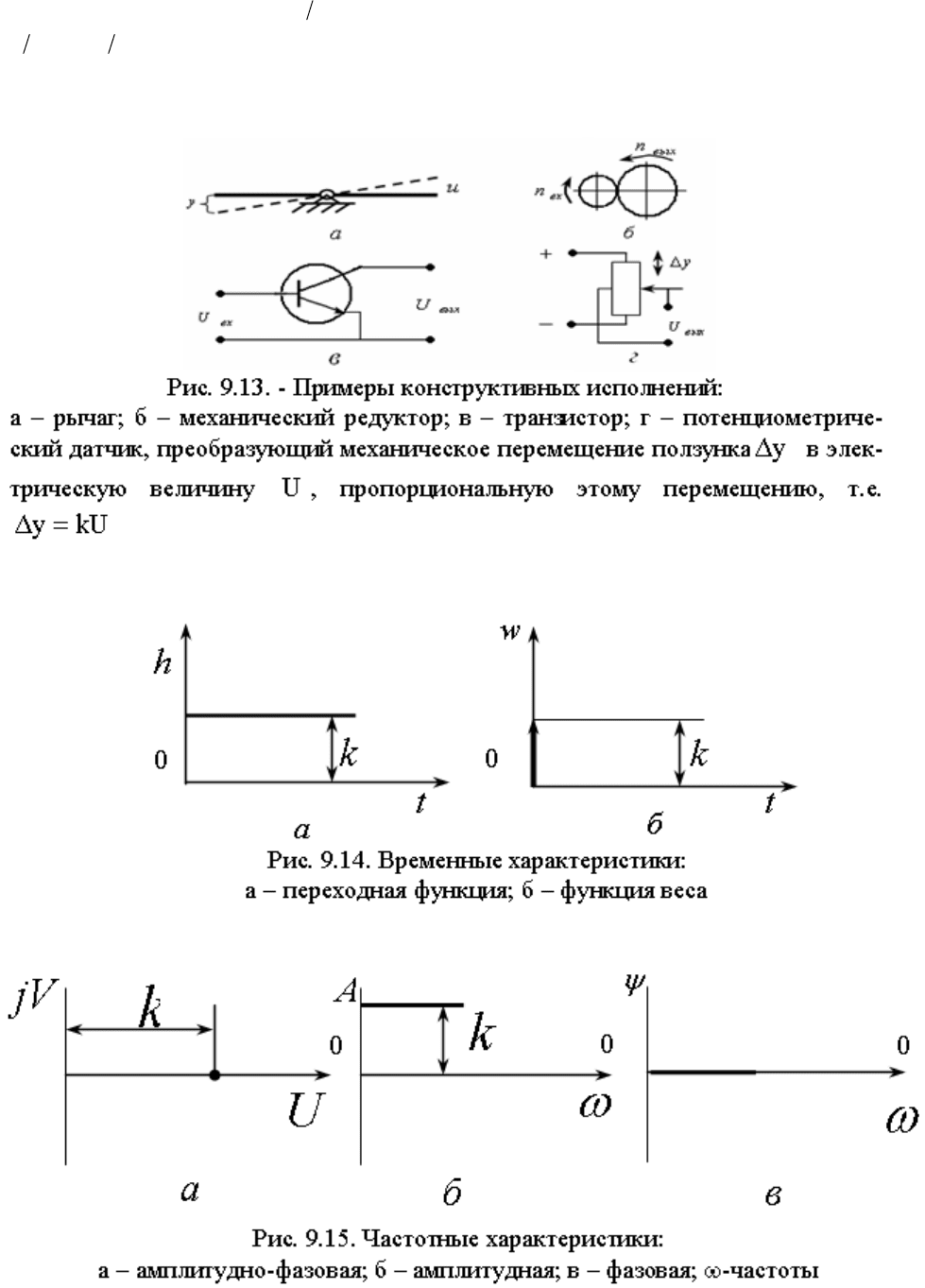
Пример. Безынерционное (пропорциональное) звено
1. Дифференциальное уравнение:
kuy
=
.
2. Конструктивное исполнение:
3. Временные характеристики:
4. Частотные характеристики:
5. Логарифмические частотные характеристики:
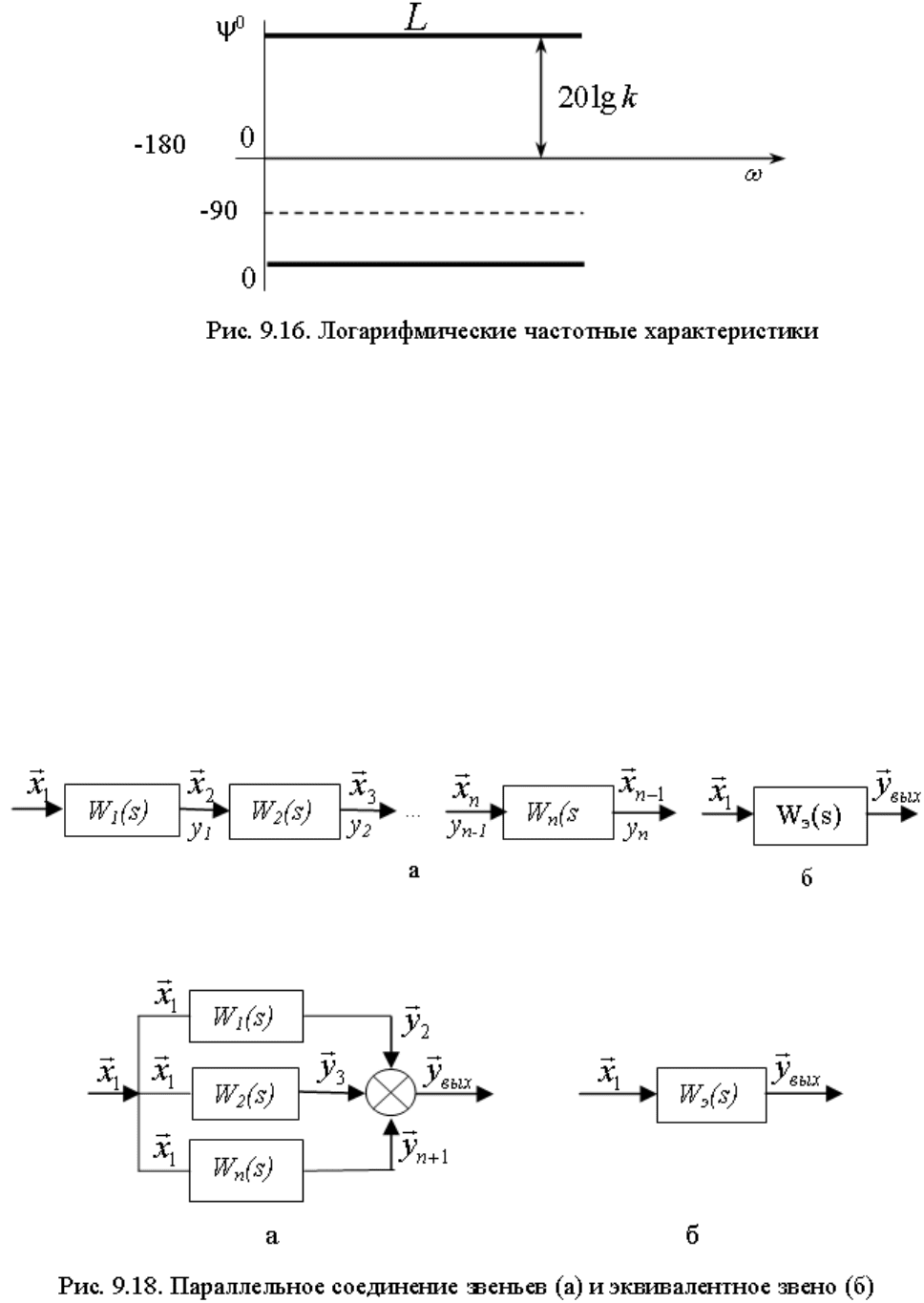
35
Примеры и характеристики остальных динамических звеньев приведены в приложении П. 1, а также в
справочниках и учебниках.
9. 8. Структурные схемы САУ и их преобразования
9.8.1. Понятие о структурной схеме САУ
САУ может быть изображена структурной схемой, состоящей из отдельных, определенным образом
связанных между собой звеньев, динамические свойства которых определяются соответствующими
передаточными
функциями. Динамические звенья, входящие в ее состав, образуют основную цепь
воздействий и цепи обратных связей. Звенья соединяются между собой линиями связей, стрелки которых
показывают направления действия сигнала. Схемы содержат узлы сравнения, или суммирования
(обозначаемые кружками с перекрещенными линиями), и точки разветвления сигнала (обозначаемые
жирно). Линии связи, отходящие от точки разветвления,
несут одни и те же сигналы.
Эти схемы позволяют более простым способом составить операторное уравнение и передаточную
функцию САУ, необходимые для исследования ее динамических свойств. Различают три основных вида
схем.
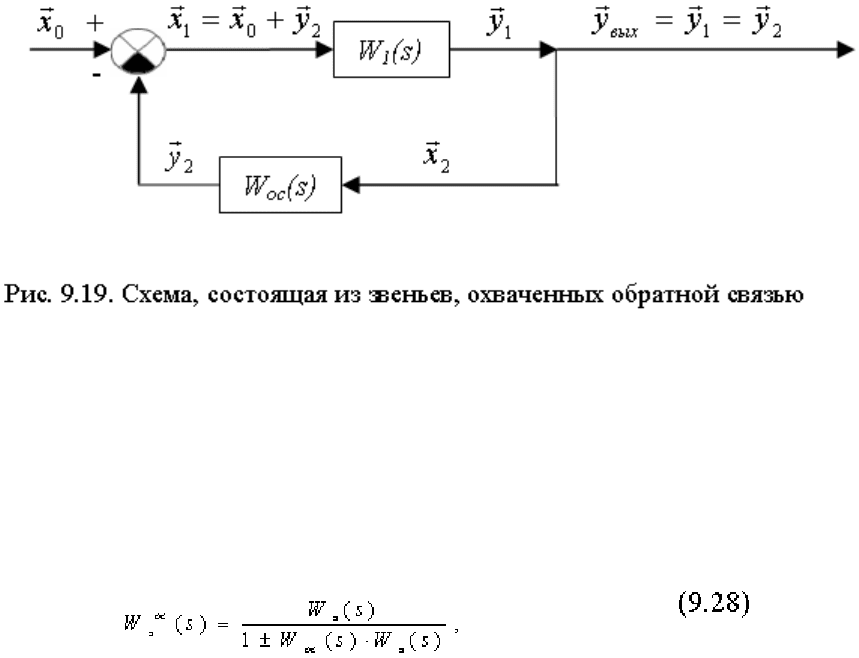
А. Состоящие из последовательно соединенных звеньев, когда выходящая величина одного звена
является входной величиной для последующего (рис. 9.17, а).
Рис. 9.17. Последовательное соединение звеньев (а) и эквивалентное звено (б)
Б. Состоящие из параллельно и согласно соединенных звеньев, когда на входы всех звеньев подается
одна и та же величина, а выходные величины суммируются (с учетом знаков) (рис. 9.18, а).
В. Состоящие из звеньев, охваченных обратной связью, когда на вход звена одновременно с входной
величиной подается и выходная величина, проходящая через звено обратной связи с передаточными
коэффициентами k
α
или функцией W
oc
(s). При этом учитывается знак выходной величины. Иногда эти схемы
36
называют схемами со звеньями, соединенными встречно-параллельно. Обычно это одна из предыдущих
схем, имеющая обратную связь (положительную или отрицательную). Положительная связь увеличивает
сигнал, а отрицательная уменьшает его (рис. 9.19).
9.8.2. Преобразование структурных схем
Сложное соединение простых звеньев может быть преобразовано в более простые соединения более
сложных звеньев. Так, последовательно соединенные звенья с передаточными функциями W
1
(s),
W
2
(s),…W
n
(s) могут быть заменены одним эквивалентным звеном с эквивалентной (приведенной)
передаточной функцией W
э
(s), являющейся произведением передаточных функций звеньев (рис. 9.17, б)
W
э
(s)=W
1
(s)·W
2
(s)·…·W
n
(s). (9.26)
Параллельно соединенные звенья заменяют эквивалентным звеном с передаточной функцией,
являющейся суммой передаточных функций звеньев (рис. 9.18, б)
W
э
(s)=W
1
(s)+W
2
(s)+…+W
n
(s). (9.27)
Эквивалентная передаточная функция САУ с обратной связью после преобразования определяется по
формуле:
где W
э
(s) - эквивалентные передаточные функции (после преобразования) последовательно или
параллельно соединенных звеньев. Знак плюс в знаменателе ставится в случае отрицательной обратной
связи, когда у суммирующего узла стоит знак минус. В случае положительной обратной связи (когда у
суммирующего узла стоит знак плюс) в знаменателе ставят минус. Правила структурных преобразований
приведены в приложении П. 2.
9.9. Применение графов для отображения САУ
Линейные дифференциальные уравнения могут быть представлены в графическом виде с помощью
структурных схем и направленных графов (бывают и ненаправленные графы). Это предложено в 1945 году
Петровым Б. Н. Наиболее распространены структурные схемы. Однако в ряде случаев применение графов
упрощает анализ сложных динамических систем и делает схемы
более компактными (см. приложение П. 3).
Граф (как и структурная схема) отображает математическую модель реальной физической системы,
образуемую совокупностью операторных уравнений динамических звеньев. Направленный граф состоит из
узлов и ветвей.
Узел (вершина) – это точка графа, отражающая зависимую или независимую переменную величину.
Ветвь (ребро, дуга) – это линия, связывающая два узла, которая характеризуется
передачей,
обозначенной соответствующим символом, и направлением, указанным стрелкой.
Часть графа, образованная последовательными ветвями, представляет путь. Прямым называют путь,
вдоль которого номера узлов возрастают, а обратным – путь, вдоль которого номера узлов убывают.
Разомкнутым считается путь, на котором данный узел встречается только один раз, замкнутым – путь,
который возвращается к своему исходному узлу.
Контур обратной связи составляют ветви, образующие
замкнутый путь.
Узлы делят на каскадные и обратной связи. Каскадным называют узел, не входящий в контур обратной
связи, и он может представлять простой каскадный узел, источник и сток. Простой каскадный узел имеет
как входящие, так и выходящие ветви. Источник – узел, отражающий независимую переменную, все ветви
которого направлены от него. Сток – узел, отражающий зависимую переменную, все ветви которого
направлены к нему. Узел обратной связи – это узел, который входит в контур обратной связи и не может
быть ни источником, ни стоком.
Узел называется зависимым, если он имеет одну или несколько входящих ветвей. Каждый входящий
сигнал определяется произведением
передачи ветви и сигнала узла, из которого выходит ветвь. Сигнал
37
данного узла X
к
равен сумме входящих сигналов: ∑х
j
T
jk
=X
k
, где j=1, 2, 3,… - индекс входящего сигнала, T
jk
-
передача от узла j к узлу k.
Передача графа эквивалентна передаточной функции динамического звена или совокупности
динамических звеньев структурной схемы. Поэтому построение графа по принципиальной физической
схеме аналогично построению структурной схемы.
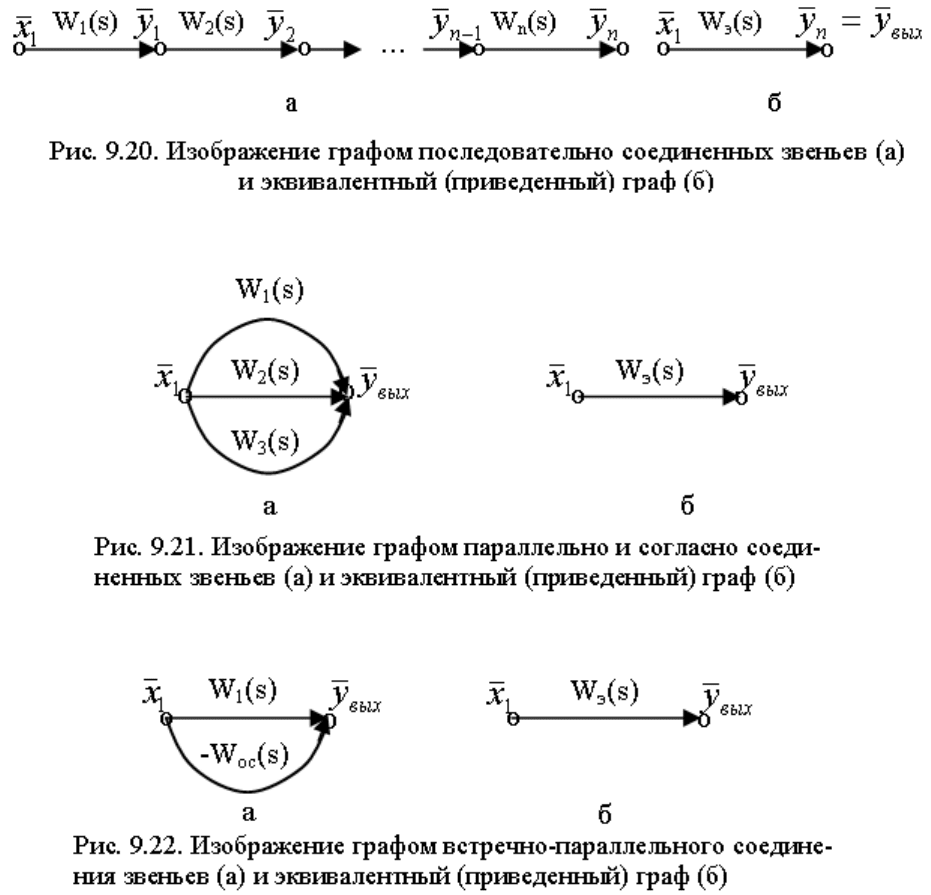
На рис. 9.20, а, б представлены изображения графом структурной схемы последовательно соединенных
звеньев (см. рис. 9.17, а) и эквивалентного приведенного графа.
Параллельно и согласно соединенные звенья структурной схемы (см. рис. 9.18, а) изображаются
графом, как показано на рис. 9.21, а. На рис. 9.21, б показан эквивалентный граф.
Встречно-параллельное соединение звеньев изображается графом следующего вида (рис. 9.22).
9.10. Синтез корректирующих устройств
9.10.1. Назначение корректирующих устройств
Проектирование (синтез) САУ обычно начинают с выбора ее структуры. Для построения рациональной
структурной схемы часто выбирают одноконтурную систему, состоящую из основной цепи воздействий и
главной обратной связи. Характер этой связи и ее коэффициент усиления выбирают, исходя из заданных
условий работы системы в установившемся
режиме. Конструктивные элементы (объекты регулирования,
двигатели, преобразователи, усилители и т.п.) применяют, как правило, стандартные, исходя из
необходимой мощности САУ и требований к ее статическим характеристикам в заданном диапазоне
изменения регулируемой величины.
Помимо удовлетворительной работы САУ в установившемся режиме, она должна иметь и хорошие
динамические показатели: устойчивость, точность и качество
переходного процесса. Если эти показатели не
достаточны, то изменяют структуру САУ для их улучшения. Это достигают двумя путями:
а) изменением основной (исходной) структуры;
б) введением в САУ специальных корректирующих звеньев (устройств) с легко изменяемыми
параметрами.
38
Так как исходная структура (схема) САУ выбирается из условия обеспечения статических режимов, то
для улучшения качества САУ чаще выбирают второй путь. При этом определяют только вид и параметры
корректирующих устройства и звеньев с определенной, заранее подобранной, передаточной функцией типа
W(s) динамических звеньев.
Коррекция обеспечивает устойчивость неустойчивой САУ, расширяет запасы и область
устойчивости,
повышает качественные показатели переходных процессов (быстродействие, колебательность,
перерегулирование и т.п.).
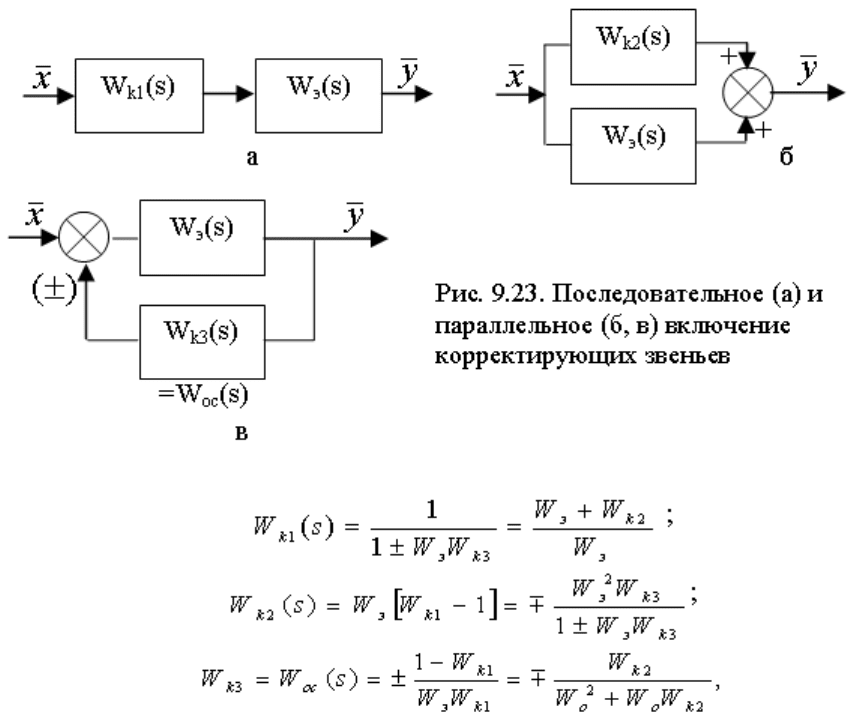
9.10.2 Включение корректирующих звеньев
Корректирующие звенья (КЗ) могут включаться последовательно (рис. 9.23, а) или параллельно (рис.
9.23, б, в) с основными звеньями САУ.
Соответственно, они делятся на последовательные и параллельные КЗ и вводятся в САУ для изменения
её динамических и
статических свойств. Для линейных САУ все виды соединений корректирующих звеньев
эквивалентны, т. е. каждое из них дает полностью подобные в динамическом отношении САУ.
Эквивалентность корректирующих звеньев вытекает из условий равенства их передаточных функций
W
k1
(s)=W
k2
(s)=W
k3
(s). Это позволило получить шесть формул перехода от корректирующих звеньев одного
типа к звеньям другого типа (для упрощения записи знак (s) в этих формулах обычно не приводят).
где W
o
– передаточная функция основных элементов САУ или объекта управления.
Линейные корректирующие звенья и устройства (пассивные и активные) разделяют на пять групп: с
запаздыванием по фазе и изменением логарифмической амплитудной характеристики (ЛАХ) на -20 дБ/дек; с
запаздыванием по фазе и изменением ЛАХ на -40 дБ/дек; с опережением по фазе и изменением ЛАХ
на +20
дБ/дек; с опережением или запаздыванием по фазе и изменением ЛАХ на ±20 дБ/дек или ±40 дБ/дек
(корректирующие звенья комбинированного типа). Здесь децибел – единица измерения отношения
амплитуд А
2
и А
1
двух сигналов при использовании логарифмической зависимости. Эту зависимость
используют, когда величина отношения весьма значительна и достигает нескольких миллионов. По
определению отношение двух сигналов, выраженное в децибелах, это дБ=20·lg(A
2
/A
1
). Например, если один
сигнал имеет амплитуду вдвое большую, чем другой, то отношение первого ко второму составляет +6 дБ,
т.к. lg2=0,301. Если же один сигнал в 10 раз больше другого, то отношение первого ко второму составляет
+20 дБ, а если один сигнал в 10 раз меньше другого, то -20 дБ. Это записывается как 20 дБ/дек. Декада
–
длина отрезка по оси абсцисс (частот) соответствующая десятикратному изменению частоты. Например,

39
частотный диапазон от 1 до 10
4
с
-1
содержит 4 декады, т.к. lg10
4
=4. Первая декада от 1 до 10 с
-1
, вторая – 10–
100 с
-1
, третья – 100–1000 с
-1
, четвертая – 1000–10000 с
-1
.
Наиболее распространенные звенья: пропорционально- дифференцирующие (ПД), пропорционально-
интегрирующие (ПИ), пропорционально-интегро-диференцирующие (ПИД). Кроме того, применяются
пропорциональные (П), интегральные (И) и дифференциальные (Д). Они применяются и в соответствующих
электронных регуляторах, схемы и характер которых представлены в приложении П. 4.
9.10.3 Корректирующие звенья последовательного типа (или последовательная коррекция)
Эти звенья применяют обычно
в САУ с электрическим сигналом в виде напряжения U постоянного
тока, которое функционально связано с ошибкой управления ε, т.е. U=f(ε). Они реализуются на пассивных
или активных RLC - элементах (чаще на элементах RC). В случае напряжения переменного тока их
применять очень сложно. Возможно выполнение корректирующих звеньев и из неэлектрических элементов,
например, механических, гидравлических
и т.п. Это связано с тем, что КЗ часто являются типовыми
динамическими звеньями. Их схемы, передаточные функции и логарифмические амплитудные частотные
характеристики (ЛАЧХ) приведены в учебниках и справочниках.
Корректирующие звенья разделяют на активные и пассивные. Активное звено в отличие от пассивного
содержит в своем составе и усилительный элемент.
Пассивные корректирующие
звенья могут быть представлены в виде обобщенной схемы (рис. 9.24, а).
Передаточная функция такого звена:
)()(
)(
)(
)(
)(
21
2
1
2
szsz
sz
sU
sU
sW
n
+
==
,
где z
1
(s), z
2
(s) – сопротивления в операторной форме.
Обобщенная схема активных звеньев представлена на рис. 9.24, б, а передаточная функция
)(
)(
)(
1
2
sZ
sZ
sW
a
−=
Последовательное включение в САУ дифференцирующих элементов (опережающих по фазе) ускоряет
протекание переходного процесса, а включение интегрирующего элемента (отстающего по фазе) – снижает
установившуюся ошибку ε.
Преимущества последовательной коррекции: 1) относительная простота включения элементов
коррекции; 2) расширение полосы пропускания частот при включении дифференцирующего элемента в цепь
регулирования.
Расчет структуры САУ обычно осуществляют графоаналитическим методом
, переходя от
передаточных функций к комплексным коэффициентам усиления, а затем к логарифмическим
характеристикам. Порядок вычисления следующий:
1. Строят ЛАЧХ исходной системы.
2. По заданным требованиям к качеству переходного процесса в проектируемой системе строят ЛАЧХ
скорректированной системы.
3. По имеющимся ЛАЧХ строят соответствующие логарифмические фазочастотные характеристики
(ЛФЧХ) и определяют имеющийся запас по
фазе и модулю.
4. Вычитанием ЛАЧХ исходной системы из ЛАЧХ скорректированной системы получают ЛАЧХ
корректирующего устройства L
k
(w).
5. По полученной ЛАЧХ корректирующего устройства подбирают наиболее простое по техническому
исполнению и его параметры.
Пример, иллюстрирующий методику синтеза при последовательном включении корректирующего
устройства, приведен на рис. 9.25.
40
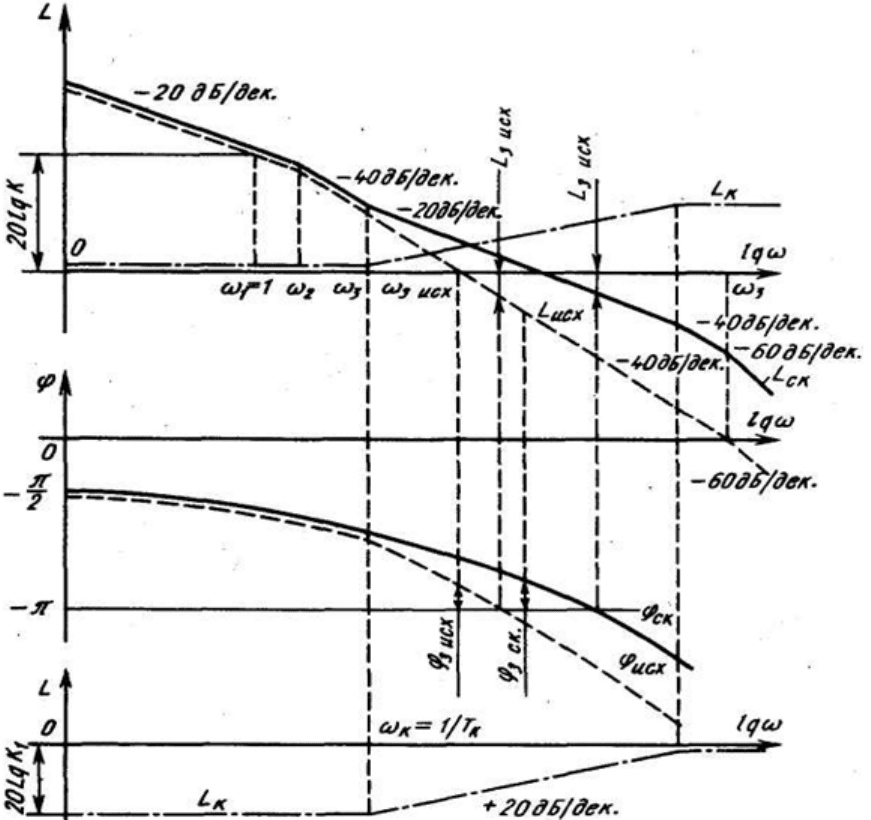
Рис. 9.25. Синтез системы с последовательной коррекцией
Исходная астатическая система имеет время переходного процесса больше того времени, которое
допустимо. Запас устойчивости по фазе меньше требуемого. Применим последовательную коррекцию.
Скорректированная ЛАЧХ, построенная вместе с соответствующей фазочастотной характеристикой с
учетом требуемого времени переходногопроцесса, имеет частоту среза ω
с.ск
больше, чем частота среза
(ω
с
.
исх
) у исходной ЛАЧХ, наклон характеристики при этой частоте -20 дБ/дек., а наклон исходной -
40дБ/дек. Как следствие уменьшения наклона у скорректированной ЛАЧХ при частоте среза запас
устойчивости по фазе увеличивается по сравнению с исходным.
Таблица 9.2. Электрические схемы, передаточные логарифмические амплитудно-частотные
характеристики типовых корректирующих устройств
