Леушин А.М., Нигматуллин Р.Р., Прошин Ю.Н. Теоретическая механика (практический курс). Задачник для физиков

Подождите немного. Документ загружается.

Теоретическая физика. Механика (практический курс) 81

Разумеется, этот выбор не является однозначным

и его целесообраз-

ность обусловлена наиболее простым видом функции Лагранжа и просто-

той уравнений Лагранжа.

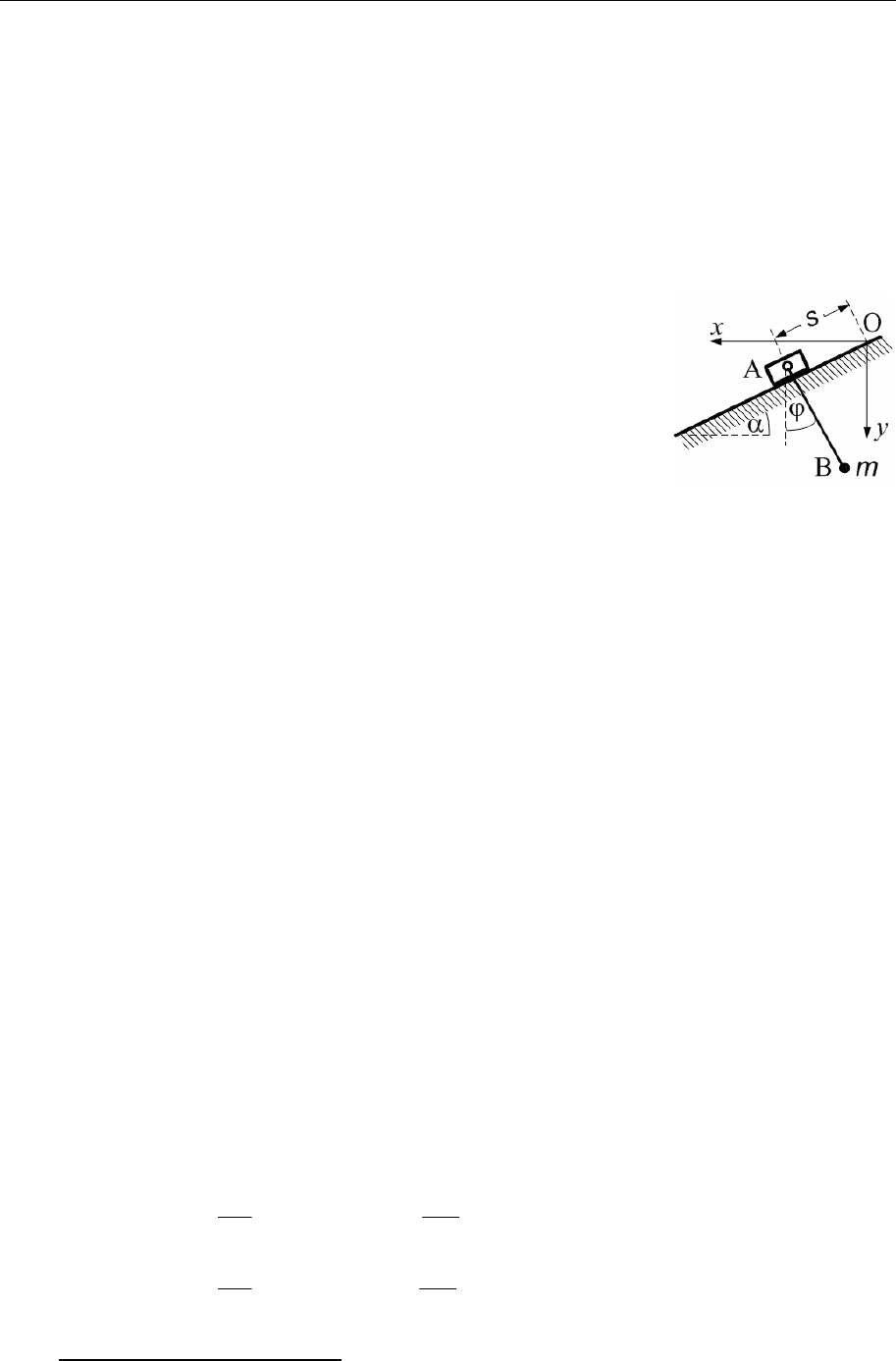
Задача 2. Груз А веса Р движется по гладкой наклонной плоскости, распо-

ложенной под углом α к горизонту. К грузу А прикреплен математиче-

ский маятник с массой m в точке B. Длина нити маятника равна l. Полагая,

что движение происходит в одной вертикальной плос-

кости, ввести обобщенные координаты системы и най-

ти соответствующие им обобщенные силы.

Реш

ение. Вычисление обобщенных сил материальной

системы является одним из существенных этапов ре-

шения задач с помощью уравнений Лагранжа 2-го рода, поэтому рассмот-

рим подробно их вычисление различными способами. Анализируемая сис-

тема имеет две степени свободы и для описания ее поведения удобно ис-

пользовать в качестве одной обобщенной координаты перемещени

е s груза

A вдоль наклонной плоскости, отсчитываемое от начала в точке O, и в ка-

честве другой − угол ϕ, который нить маятника образует с вертикалью.

Способ (а). Для нахождения соответствующих этим координатам обобщен-

ных сил Q

и Q

воспользуемся вначале формулой (5.11). На систему дейст-

вуют две активные силы:

, равная по модулю весу P груза A, и F

– вес ма-

ятника, равный по модулю mg, обе направлены вертикально вниз. Вводя де-

картовую систему координат, как показано на рисунке, и проектируя на ее

оси силы

и F

и радиус-векторы груза A (r

) и частицы (r

), будем иметь

(0, P), F

(0, mg)

(s cosα, s sinα), r

(s cosα − l sinϕ, s sinα + l cosϕ).

Для проекций частных производных по обобщенным координатам от ра-

диус-векторов найдем

(cos ,sin ), (cos ,sin ),

(0,0), ( cos , sin ).

∂

αα αα

∂∂

−

ϕ− ϕ

∂ϕ ∂ϕ

В качестве обобщенных координат можно использовать, например, x

, x

; x

, y

; x

,ψ и т.д.

Уравнения Лагранжа 82

Вычисляя суммы необходимых скалярных произведений, из (5.11) получа-

ем требуемые обобщенные силы

sin sin ( )sin ,

0sin sin

QP mg Pmg

Qmgl mgl

=α+ α=+ α

=− ϕ=− ϕ

Способ (б). Используем теперь наиболее распространенный прием вычис-

ления обобщенных сил как коэффициентов при вариациях обобщенных

координат в выражении суммы элементарных работ активных сил на вир-

туальных перемещениях (5.12). Дадим системе два независимых обобщен-

ных виртуальных перемещения: δs, направленное параллельно наклонной

плоскости в сторону возрастания координаты s, т.е. вниз, и δϕ − в сторон

возрастания угла ϕ, т.е. против часовой стрелки от вертикального направ-

ления. Учитывая независимость виртуальных перемещений δs и δϕ, при

вычислении суммы работ активных сил будем давать системе виртуальное

перемещение, соответствующее искомой обобщенной силе, а второе вир-

туальное перемещение будем при этом считать равным нулю. Так, для оп-

ределения обобщенной силы Q

дадим системе виртуальное перемещение

δs, а δϕ будем считать равным нулю. Это значит, что при фиксированном

значении угла поворота маятника ϕ вся система, состоящая из груза и ма-

ятника, перемещается поступательно на δs.

На виртуальном перемещении δs сумма работ активных сил имеет вид

δA = P δs sinα + mg δs sinα = ( P + mg ) sinα δs. (5.24)

Обобщен

ной силой Q

является коэффициент пропорциональности, стоя-

щий при δs в формуле (5.24), т.е.

= ( P + mg ) sinα.

Для определения обобщенной силы Q

дадим системе виртуальное пере-

мещение δϕ, а δs будем считать равным нулю. Это значит, что груз A на-

ходится на наклонной плоскости в покое, а нить маятника отклоняется на

угол δϕ против часовой стрелки. Сумма работ активных сил на виртуаль-

ном перемещении δϕ равна:

δA = − mg l sinϕ δϕ. (5.25)

Обобщенной силой Q

является коэффициент пропорциональности, стоя-

Теоретическая физика. Механика (практический курс) 83

щий при δϕ в формуле (5.25), т.е.

= − mg l sinϕ.

Способ (в). Вследствие того, что обе активные

силы, действующие на сис-

тему, носят потенциальный

характер, интересующие нас обобщенные си-

лы могут быть вычислены еще одним способом. Согласно формуле (5.13)

обобщенные силы являются частными производными с обратным знаком

от потенциальной энергии системы. В данном случае обобщенные силы Q

и Q

мы можем найти по формулам: ,

∂

=− =−

∂

∂ϕ

. Для этого

предварительно следует вычислить потенциальную энергию системы

U(s, ϕ). Принимая за нуль потенциала его значение в точке O, для потен-

циальной энергии системы будем иметь

U(s, ϕ) = −Ps sinα − mg (s sinα + l cosϕ) = − (P + mg) s sinα − mg l cosϕ.

Дифференцируя функцию U(s, ϕ) частным образом по s и по ϕ, для соот-

ветствующих обобщенных сил найдем величины

(

)sin , sin

QPmg Q mgl

=+ α =− ϕ,

совпадающие с полученными выше выражениями.

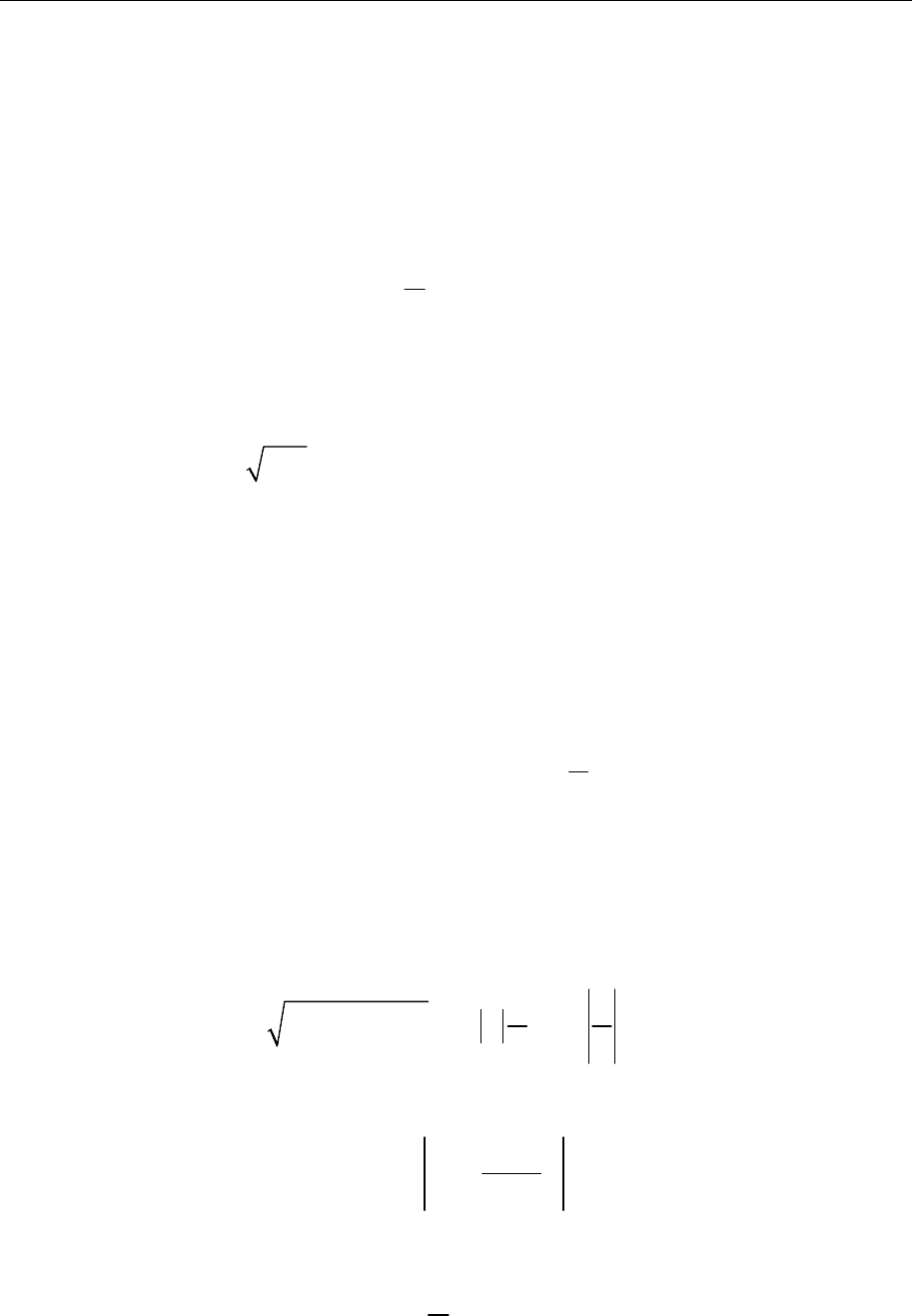
Задача 3. Частица массы m подвешена на невесомой и не-

растяжимой нити длины l, прикрепленной в неподвижной

точке O, и может совершать движение в вертикальной

плоскости xOy. Предполагая, что система находится в поле

силы тяжести, найти закон движения частицы и натяжение

нити T, используя для этой цели уравнения Лагранжа 1-го

рода.

Решение. Поскольку частиц

а, образующая маятник, все время находится в

плоскости xOy и на одном и том же расстоянии, равном l, от точки O, то

два уравнения связи, наложенные на нее, имеют вид

2222

(, ,) 0,

(, ,) 0.

fxyz x y z l

fxyz z

=++−=

(5.26)

Записывая уравнения Лагранжа 1-го рода в соответствии с (5.6), получаем

Уравнения Лагранжа 84

2222

(, ,) 0,

mx mg x

my y

mz z

fxyz x y z l

fxyz z

⎧

=+λ

⎪

=λ

⎪

=λ +λ

⎨

⎪

=++−=

⎪

⎩

(5.27)

систему пяти уравнений для определения пяти неизвестных: x(t), y(t), z(t),

(t) и λ

(t). Так как z

0, то из третьего уравнения находим λ

= 0, а из

второго уравнения имеем

λ=

. После умножения первого уравнения

системы (5.27) на y и вычитания из него второго уравнения, умноженного

на x, получим

()mxy yx mgy

−

&& &&

. (5.28)

Выразим координаты x и y через угол ϕ, который нить маятника образует с

осью Ox,

x = l cosϕ, y = l sinϕ.

Используя эту замену и вычисляя производные

sin , cos ,

cos sin ,

sin cos ,

xl yl

xl l

yl l

=− ϕ ϕ = ϕ ϕ

=− ϕ ϕ− ϕ ϕ

=− ϕ ϕ+ ϕ ϕ

&&&

уравнению (5.28) можно придать известную форму дифференциального

уравнения колебаний математического маятника

sin 0

+ϕ=

Записав уравнение в виде

()

sin cos

ddd

ϕϕ=− ϕϕ= ϕ

и интегрируя его при начальных условиях: при t = 0 ϕ = 0,

ϕ=ϕ

, будем

иметь

2(1cos)

ϕ=ϕ− − ϕ

. (5.29)

Теоретическая физика. Механика (практический курс) 85

Кстати сказать, это уравнение мы можем получить и из закона сохранения

энергии. Дальнейшее интегрирование этого нелинейного уравнения пред-

ставляет известные трудности, поэтому решим исходное уравнение при-

ближенно, допустив, что колебания малы. Разлагая sinϕ в ряд вблизи точки

ϕ = 0 и сохраняя только первый член разложения, уравнению придадим вид

+ϕ=

Решая его, находим

00 0

() sinttϕ=ϕω ω

где величина

/glω= является частотой малых колебаний частицы.

Возвращаясь к исходным переменным, получаем в этом приближении ко-

ординаты частицы x и y как функции времени

(

)

(

)

00 0 00 0

( ) sin sin , ( ) cos sin

tl tytl t= ωϕω = ωϕω

Найдем теперь натяжение нити. В соответствии с формулами (5.5) по-

лучаем

Txmy

Tymy

=λ =

⎧

⎪

=λ =

⎨

⎪

⎩

и, следовательно, величина натяжения нити определяется выражением

222

xyz

TTTTmy ml

=++= =

или

cos

sin

Tml

ϕ− ϕ

&&&

Так как

sin

=− ϕ

определяется формулой (5.29), то

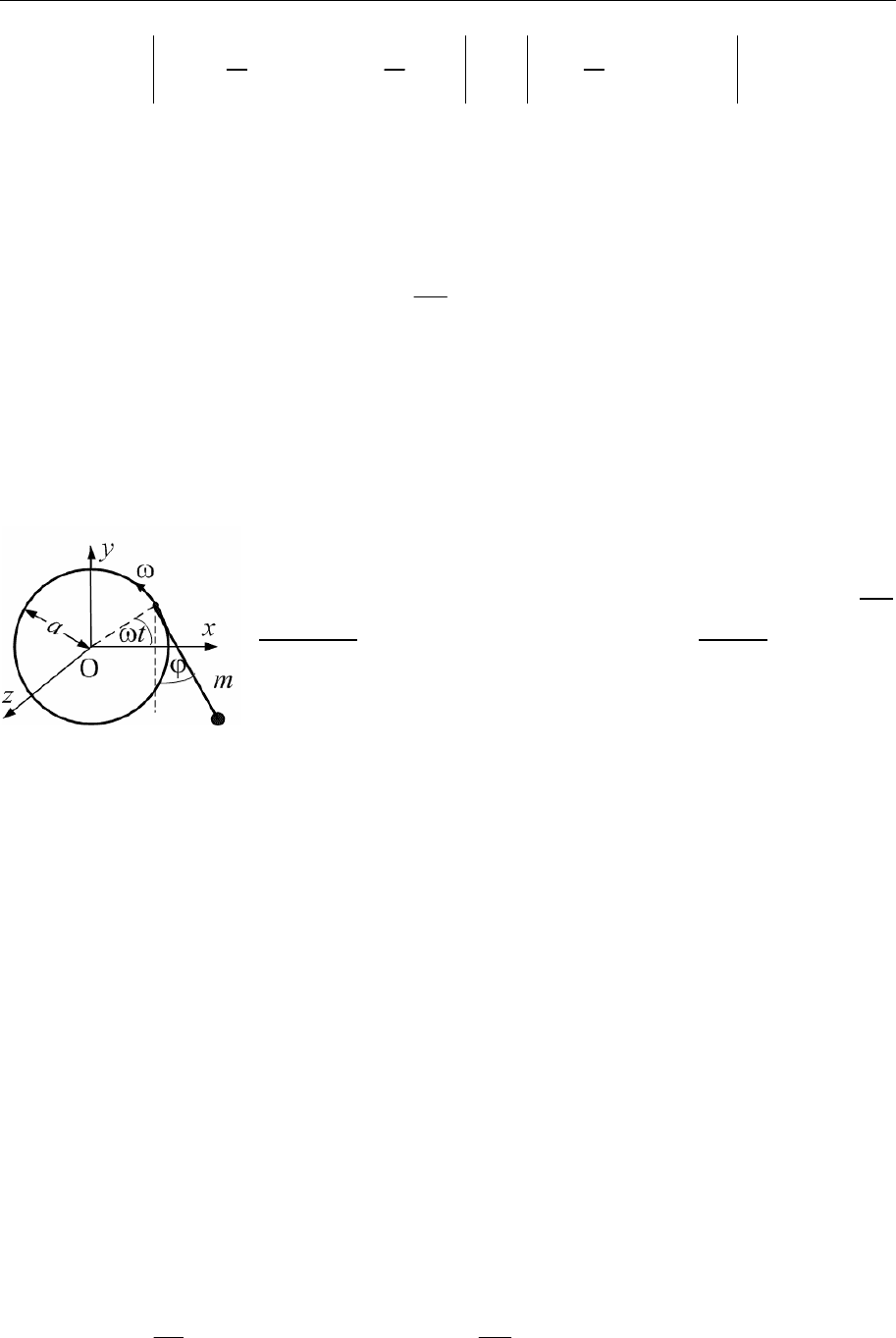
Уравнения Лагранжа 86

2 (1 cos ) cos (2 3cos )

gg g

Tml ml

ll l

=ϕ− −ϕ+ ϕ=ϕ− − ϕ

Из этого уравнения следует, что связь в виде нити будет удерживающей,

если 0T ≥ при ϕ = π. Это условие выполняется, когда начальная угловая

скорость

удовлетворяет неравенству

≥=ω

Задача 4. Найти функцию Лагранжа и составить уравнения Лагранжа 2-го

рода плоского маятника, точка подвеса которого равномерно вращается по

вертикальной окружности с постоянной частотой

. Радиус окружности

равен а, и частица с массой m подвешена на нити длиной l.

Решение. Вследствие того, что движение является

плоским и точка подвеса маятника двигается по за-

данному закону, система обладает одной степенью

свободы. За обобщенную координату примем угол ϕ,

который нить образует с вертикалью. Будем для кон-

кретности полагать, что в начальный момент t = 0 точка подвеса маятника

находилась на оси Ox. На систему действует только одна сила – сила тяже-

сти частицы с массой m, и она потенциальна. Функция Лагранжа L будет

равна разности кинетической и потенциальной эне

ргии частицы. Из-за то-

го, что связь, вынуждающая точку подвеса маятника вращаться по окруж-

ности, является нестационарной, кинетическая энергия системы будет со-

держать нулевой, линейный и квадратичный члены по обобщенной скоро-

сти ϕ

(5.19). Для их нахождения мы можем воспользоваться выражениями

(5.20) и (5.21), приняв во внимание тот факт, что частица в системе всего

одна и эти выражения будут значительно упрощены. Проектируя радиус-

вектор частицы на оси x и y, будем иметь

( cos sin , sin cos )atl atlω+ ϕ ω− ϕ

r .

Для частных производных найдем

( sin , cos ), ( cos , sin ).ata t ll

∂∂

−ω ω ω ω ϕ ϕ

∂∂ϕ

Теоретическая физика. Механика (практический курс) 87

Следовательно, кинетическая энергия будет иметь вид

22 22

(sin cos cos sin )

sin( )

ma ml

Tmalt t

ma ml

mal t

ωϕ

=−ωϕωϕ−ωϕ+=

ωϕ

=−ωϕω−ϕ+

Этот же вид кинетической энергии можно получить иначе, не исполь-

зуя выражений (5.19)−(5.21), а просто, взяв формулу T = mv

/2, подставив в

нее квадрат скорости частицы в декартовой системе координат

222

vxy=+

, предварительно найдя проекции скорости на декартовы оси как

производные от выражений декартовых координат, представленных через

обобщенную координату ϕ. Записывая координаты и вычисляя скорости

cos sin , sin cos ,

sin cos , cos sin ,

atl xa tl

ya tl ya tl

=ω+ϕ=−ωω+ϕϕ

=ω−ϕ=ωω+ϕϕ

для кинетической энергии получаем то же самое выражение

22 22

() sin()

22 2

mml ma

Txy mal t

=+= −ωϕω−ϕ+

Записав потенциальную энергию частицы (при выборе нуля потен-

циала на уровне оси Ox)

(sin cos)Umga tl=ω−ϕ

и вычитая ее из кинетической энергии, для функции Лагранжа получим

выражение

22 22

( , , ) sin( ) ( sin cos )

ml ma

Lt mal t mgatl

ϕω

ϕϕ = − ωϕ ω −ϕ + − ω − ϕ

Составленную функцию Лагранжа можно существенно упростить, ес-

ли иметь в виду, что к ней согласно (5.23) можно присоединить полную

производную по времени от произвольной функции координат и времени,

и такая трансформация ее ни к каким физическим последствиям не приве-

дет

. Так как в этот разряд возможных присоединяемых слагаемых попа-

Но может существенно изменить вид функции Лагранжа и упростить получение уравнений

Лагранжа.

Уравнения Лагранжа 88

дают все константы и все слагаемые, зависящие только от времени, то их

сразу в функции Лагранжа можно опустить. В нашем случае таковыми яв-

ляются члены:

ma ω /2 и sinmga t−ω. Более того, если мы вычислим пол-

ную производную по времени от выражения cos( )mal t

ω−ϕ

[]

cos( ) sin( ) sin( )

mal t mal t mal t

ω ω −ϕ =− ω ω −ϕ + ωϕ ω −ϕ

то обнаружим, что слагаемое sin( )mal t

−

ωϕ ω − ϕ

нашей функции Лагранжа

можно представить в виде

[]

sin( ) sin( ) cos( )

mal t mal t mal t

− ωϕ ω −ϕ =− ω ω −ϕ − ω ω −ϕ

в котором первый член в правой части имеет более простой вид (вместо

обобщенной скорости ϕ

в качестве множителя содержит постоянную уг-

ловую скорость ω), а второй член опять является полной производной по

времени от функции координат и времени и его можно тоже беспрепятст-

венно опустить. Имея все эти рассуждения в виду, найденной выше функ-

ции Лагранжа мож

но, без ущерба для существа дела, придать следующий,

более простой по сравнению с первоначально полученным, вид

( , , ) sin( ) cos

L t mal t mgl

ϕϕ = − ω ω −ϕ + ϕ

Для составления уравнения Лагранжа 2-го рода в виде (5.15) вычисля-

ем частную производную от функции Лагранжа по обобщенной скорости

и затем полученное выражение полным образом дифференцируем по

времени, получаем

⎛⎞

∂

=ϕ

⎜⎟

∂ϕ

⎝⎠

. Далее вычисляем частную производ-

ную от функции Лагранжа по обобщенной координате

cos( ) sin

mal t mgl

∂

=− ω ω −ϕ − ϕ

∂ϕ

Из полученного первого результата вычитаем второй и составленную раз-

ность приравниваем нулю. Получаем уравнение Лагранжа

cos( ) sin 0ml mal t mglϕ+ ω ω −ϕ + ϕ=

которое после сокращения на ml приобретает окончательный вид

Теоретическая физика. Механика (практический курс) 89

cos( ) sin 0la t gϕ+ ω ω −ϕ + ϕ=

Задача 5. Составить функцию Лагранжа и получить уравнения Лагранжа

для следующих свободных систем:

а) свободно двигающаяся частица;

б) линейный гармонический осциллятор;

в) частица, двигающаяся в центрально симметричном поле под действием

силы притяжения, обратно пропорциональной квадрату расстояния до си-

лового центра.

Решение. а) Так как на свободную частицу не действуют никакие силы, то

ее функция Лагран

жа будет состоять только из кинетической энергии. Рас-

сматривая в качестве обобщенных координат обычные декартовые коор-

динаты x, y, z (мы это можем сделать, поскольку никаких связей нет), для

функции Лагранжа будем иметь

222

()

xyz=++

Составляя уравнения Лагранжа

0, 0, 0

dL L dL L dL L

dtxx dtyy dtzz

⎛⎞

∂∂ ∂∂ ∂∂

⎛⎞ ⎛⎞

−= −= −=

⎜⎟ ⎜⎟

⎜⎟

∂∂ ∂∂ ∂∂

⎝⎠ ⎝⎠

⎝⎠

найдем

0, 0, 0mx my mz===

&& &&

Видим, что уравнения Лагранжа являются обычными уравнениями движе-

ния свободной частицы в декартовых координатах, из которых с началь-

ными условиями (при

0 и t == =rr vv) получаем закон движения сво-

бодной частицы

()rt t

+vr

б) Линейным гармоническим осциллятором называют частицу массы m,

двигающуюся по одной прямой под действием силы вида Fkx=− , где k −

постоянный положительный коэффициент. Найдем потенциальную энер-

гию, соответствующую данной потенциальной силе. Имеем

(

)

grad () () ()/

Ux Ux dUx dx kx=− =−∇ =− =−Fee

Уравнения Лагранжа 90

Отсюда получаем

()dU x

= и поэтому

()

Ux= ,

если полагать, что потенциал равен нулю при x = 0. Так как кинетическая

энергия осциллятора

T =

то для функции Лагранжа найдем

mx kx

L =−

Составляя уравнение Лагранжа, будем иметь

0mx kx

Определяя частоту ω

= k/m, получаем известное уравнение движения ос-

циллятора в виде

ω=

в) В силу того, что частица в любом центрально симметричном поле дви-

жется в плоскости, перпендикулярной сохраняющемуся угловому момен-

ту, для описания ее движения на плоскости xOy удобно ввести полярные

координаты ρ и ϕ, которые и будут играть роль обобщенных координат.

Так как сила притяжения, действующая на частицу, обратно пропорцио-

нальна кв

адрату расстояния до силового центра, который будем считать

находящимся в начале координат, то ее можно записать в виде

()

ρ=−

где α − константа взаимодействия. Полагая потенциал равным нулю в бес-

конечно удаленной точке от силового центра, для потенциальной энергии

частицы найдем

()U

−

Так как квадрат скорости частицы в полярной системе координат имеет