Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection
Подождите немного. Документ загружается.

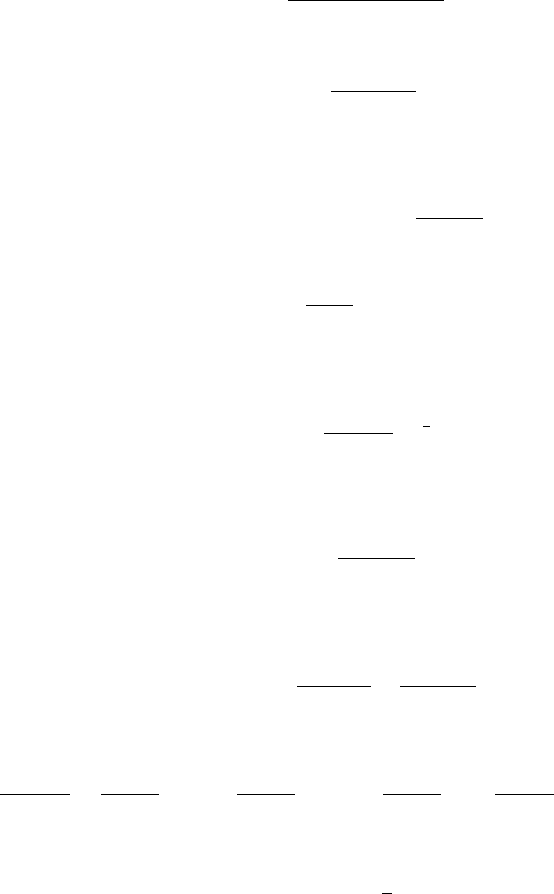
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
740 Principles of Radiation Interaction in Matter and Detection
and g
n
are the effective neutralino-proton and neutralino-neutron coupling constants
for SI interactions; F
SI
is the spin-independent form factor [Eq. (10.25)]. The recoil
energy, E
R
, is given by
E
R
=
µ
2
χN
v
2
(1 − cos θ
∗
)
m
N
, (10.22)
where µ
χN
is the neutralino–nucleus (N ) reduced mass
µ
χN
=
m
χ
m
N
m
χ
+ m
N
and θ
∗
is the scattering angle in the neutralino–nucleus center-of-mass frame. From
Eq. (10.22), one obtains:
E
R,max
= E
R
(θ
∗
= π) =
2µ
2
χN
v
2
m
N
(10.23)
and, therefore,
v
2
=
m
N
2µ
2
χN
E
R,max
. (10.24)
As above mentioned, F
SI
(E
R
) is the spin-indep endent form factor and follow-
ing [Engel (1991)]; it is written as
F
SI
(E
R
) = 3
J
1
(qR
0
)
qR
0
e
−
1
2
s
2
q
2
, (10.25)
where q
2
= 2m
N
E
R
is the squared three-momentum transfer and J
1
is the spherical
Bessel function of index 1. The parameter s is the thickness parameter of the nuclear
surface, s ∼ 0.9 fm. The parameter R
0
is related to the nuclear radius and thickness,
R
0
=
p
R
2
− 5s
2
with R = 1.2 A
1/3
fm. In the case of
19
F, R = 3.2 fm, R
0
= 2.5 fm with s =
0.9 fm. The form factor is normalized to unity for q
2
= 0. Indeed, we have
J
1
(qR
0
) =
sin(qR
0
)
(qR
0
)
2
−
cos(qR
0
)
qR
0
. (10.26)
In the limit qR
0
→ 0, Eq. (10.26) becomes:
J
1
(qR
0
)
qR
0
=
1
(qR
0
)
3
"
qR
0
−
(qR
0
)
3
6
+ . . .
#
−
1
(qR
0
)
2
"
1 −
(qR
0
)
2
2
+ . . .
#
, (10.27)
i.e.,
J
1
(qR
0
) =
1
3
. (10.28)
Therefore, for qR
0
→ 0, one obtains
F
SI
(0) = 1. (10.29)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Superheated Droplet (Bubble) Detectors and CDM Search 741
Equation (10.25) is obtained from a density [Helm (1956)] in the form
R
ρ
0
(r
0
)ρ
1
(r − r
0
) d
3
r
0
, where ρ
0
is constant inside the radius R
0
and
ρ
1
(r) = exp
µ
−
1
2
s
2
q
2
¶
.
The Fourier transform of the function ρ, which represents a nearly constant interior
density and a surface of thickness s, gives Eq. (10.25).
Integrating Eq. (10.21) over E
R
, one finds
σ
χN
SI
(v) =
Z
E
R,max
0
µ
dσ
dE
R
¶
SI
dE
R
; (10.30)
using Eq. (10.24),
σ
χN
SI
(v) =
4G
F
2
µ
2
χN
π
[Zg
p
+ (A − Z)g
n
]
2
1
E
R,max
Z
E
R,max
0
[F
SI
(E
R
)]
2
dE
R
(10.31)
or
σ
χN
SI
(v) =
4G
F
2
µ
2
χN
π
[Zg
p
+ (A − Z)g
n
]
2
G
SI
(v), (10.32)
where one has defined
G
SI
(v) =
1
E
R,max
Z
E
R,max
0
[F
SI
(E
R
)]
2
dE
R
. (10.33)
The quantity G
SI
(v) was calculated for several nuclei (
19
F,
73
Ge,
127
I) and the
results are shown in Fig. 10.13.
One can establish the following identity:
·
1 −
g
p
− g
n
g
p
+ g
n
µ
1 −
2Z
A
¶¸
2
A
2
·
g
p
+ g
n
2
¸
2
=
·
g
p
+ g
n
− (g
p
− g
n
)
µ
1 −
2Z
A
¶¸
2
×
·
1
g
p
+ g
n
¸
2
A
2
·
g
p
+ g
n
2
¸
2
= [Zg
p
+ (A − Z)g
n
]
2
. (10.34)
Therefore, Eq. (10.32) can be rewritten as:
σ
χN
SI
(v) =
4G
F
2
µ
2
χN
π
·
g
p
+ g
n
2
¸
2
·
1 −
g
p
− g
n
g
p
+ g
n
µ
1 −
2Z
A
¶¸
2
A
2
G
SI
(v) (10.35)
or
σ
χN
SI
(v) =
4G
F
2
µ
2
χN
π
g
2
A
2
G
SI
(v), (10.36)
where one has defined
g =
g
p
+ g
n
2
·
1 −
g
p
− g
n
g
p
+ g
n
µ
1 −
2Z
A
¶¸
. (10.37)
In the limit v → 0, G
SI
(0) → 1 and Eq. (10.36) becomes
σ
χN
SI
(0) =
4G
F
2
µ
2
χN
π
g
2
A
2
. (10.38)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
742 Principles of Radiation Interaction in Matter and Detection
0 0.002 0.004 0.006 0.008 0.01 0.012 0.014 0.016
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
β = v/c
G
SI
for a 50 GeV neutralino
19
F
73
Ge
127
I
Fig. 10.13 G
SI
[Eq. (10.33)] as a function of β = v/c for
19
F,
73
Ge,
127
I.
Since Z/A is nearly constant for the nuclei typically used in direct searches for dark
matter particle (Table 10.1), the coupling constant g is approximately independent
of the target nucleus used in the experiment. Therefore, one defines a so-called
generalized spin-independent neutralino–nucleon(p) cross section
σ
χp
SI
=
4G
F
2
µ
2
χp
π
g
2
, (10.39)
which is related to the spin-independent neutralino–nucleus(N) cross section via
σ
χp
SI
=
µ
2
χp
µ
2
χN
σ
χN
SI
A
2
. (10.40)
Furthermore, one has the relation between g
p
and g
n
:
g
p
=
1
Z
q
σ
χN
SI
(0)π
2G
F
µ
χN
+
µ
1 −
A
Z
¶
g
n
. (10.41)
Then, in principle one can estimate the coupling g
p
and g
n
from the experimental
limits on spin-independent neutralino cross sections on two different nuclei.
10.2.1.2 Spin-Dependent or Incoherent Cross Section
The spin-dependent (SD) cross section is given by (see for instance [Bottino et al.
(1997); Tovey et al. (2000)] and references therein)
σ
SD
χN
(v) =
Z
E
R,max
0
µ
dσ
dE
R
¶
SD
dE
R
, (10.42)
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Superheated Droplet (Bubble) Detectors and CDM Search 743
where
µ
dσ
dE
R
¶
SD
=
2G
F
2
m
N
πv
2
8Λ
2
J(J + 1) [F
SD
(E
R
)]
2
, (10.43)
F
SD
(E
R
) is the spin-dependent form factor and
Λ =
1
J
[a
p
hS
p
i + a
n
hS
n
i] . (10.44)
hS
p
i and hS
n
i are the expectation values of the proton and neutron spin within
the nucleus N, respectively; a
p
and a
n
are the neutralino–proton and neutralino–
neutron coupling coefficients, respectively. We have:
hS
p
i = hN |S
p
|Ni =
1
2
if N = 1 proton and hS
p
i = 0.441 if N =
19
F;
hS
n
i = hN |S
n
|Ni =
1
2
if N = 1 neutron and hS
n
i = −0.109 if N =
19
F.
Using Eq. (10.24), we obtain
σ
SD
χN
(v) =
4G
F
2
µ
2
χN
π
£
8Λ
2
J(J + 1)
¤
1
E
R,max
Z
E
R,max
0
]F
SD
(E
R
)]
2
dE
R
(10.45)
or
σ
SD
χN
(v) =
4G
F
2
µ
2
χN
π
£
8Λ
2
J(J + 1)
¤
G
SD
(v) (10.46)
with
G
SD
(v) =
1
E
R,max
Z
E
R,max
0
F
SD
2
(E
R
)dE
R
. (10.47)
If one notes that v → 0 (β = v/c ∼ 220/300, 000 ∼ 7 × 10
−4
) and G
SD
(v) → 1,
therefore, one can write Eq. (10.46) as
σ
SD
χN
(0) =
4G
F
2
µ
2
χN
π
8(J + 1)
J
[a
p
hS
p
i + a
n
hS
n
i]
2
. (10.48)
One usually rewrites Eq. (10.48) as
σ
SD
χN
(0) = 4G
F
2
µ
2
χN
C
SD
N
, (10.49)
where the factor
C
SD
N
=
8(J + 1)
Jπ
[a
p
hS
p
i + a
n
hS
n
i]
2
is called the total enhancement factor in the spin-dependent neutralino–nucleus
elastic cross section. If one defines the nucleon contribution to the total enhancement
factor as
C
SD
nucleon(N)
=
8
π
(J + 1)
J
a
2
nucleon
hS
nucleon
i
2
= F a
2
nucleon
hS
nucleon
i
2
(10.50)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
744 Principles of Radiation Interaction in Matter and Detection
with
F =
8(J + 1)
πJ
,
one has
a
nucleon
hS
nucleon
i = ±
s
C
nucleon(N)
SD
F
. (10.51)
Introducing Eq. (10.51) in Eqs. (10.48, 10.49), one finds:
σ
SD
χN
(0) = 4G
F
2
µ
2
χN
h
q
C
SD
p(N)
±
q
C
SD
n(N)
i
2
. (10.52)
One can express the total neutralino cross section on nucleus from the cross section
on nucleons as
σ
SD
χN
(0) =
³
q
4G
F
2
µ
2
χN
C
SD
p(N)
±
q
4G
F
2
µ
2
χN
C
SD
n(N)
´
2
. (10.53)
The calculation of hS
p
i and hS
n
i for nuclear shells models shows non-vanishing
proton and neutron contributions to the nuclear spin [Tovey et al. (2000)]. The
supersymmetric and nuclear degrees of freedom are generally not decoupled. This
prevents the direct extraction of a universal χ–nucleon cross section contrary to
the spin independent case [Bottino et al. (1997)]. In order to compare experiments
performed on different nuclei, one introduces neutralino-proton, neutralino-neutron
cross sections instead of using neutralino–nucleus cross sections. Such a formalism
can be found in [Tovey et al. (2000); Genest and Leroy (2004); Giuliani (2005)], for
instance.
Equation (10.52) can be rewritten as
σ
SD
χN
(0) =
³
q
σ
SD
p(N)
±
q
σ
SD
n(N)
´
2
, (10.54)
where one has defined the proton and neutron contributions to the total cross sec-
tion:
σ
SD
nucleon(N)
= 4G
F
2
µ
2
χN
C
SD
nucleon(N)
. (10.55)
One has also the cross sections for isolated nucleon
σ
SD
nucleon
= 4G
F
2
µ
2
χp
C
SD
nucleon
. (10.56)
From Eqs. (10.55, 10.56), one finds
σ
SD
nucleon
σ
SD
nucleon(N)
=
4G
F
2
µ
2
χnucleon
C
nucleon
SD
4G
F
2
µ
2
χN
C
nucleon(N)
SD
. (10.57)
One has a relation between the cross sections obtained for protons (neutrons)
in a nucleus and cross sections for free protons (free neutrons):
σ
SD
p
= σ
SD
p(N)
µ
2
χp
µ
2
χN
C
p
SD
C
p(N)
SD
(10.58)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Superheated Droplet (Bubble) Detectors and CDM Search 745
and
σ
SD
n
= σ
SD
n(N)
µ
2
χn
µ
2
χN
C
n
SD
C
n(N)
SD
. (10.59)
When one achieves the limit in the number of events in a direct detection experi-
ment, one assumes that the total neutralino–nucleus (N) cross section is dominated
by the proton (or neutron) contribution only , i.e.,
σ
SD
χN
∼ σ
SD
p(N)
(10.60)
and
σ
SD
χN
∼ σ
SD
n(N)
. (10.61)
Equations (10.58, 10.59) become
σ
SD
p
= σ
SD
χ(N)
µ
2
χp
µ
2
χN
C
p
SD
C
p(N)
SD
(10.62)
and
σ
SD
n
= σ
SD
χ(N)
µ
2
χn
µ
2
χN
C
n
SD
C
n(N)
SD
. (10.63)
The use of the ratios C
SD
p
/C
SD
p(N)
and C
SD
n
/C
SD
n(N)
ensures the cancellation of the
a
p
and a
n
terms which makes the calculation model-independent.
If σ
SDlim
χN
is the upper limit of neutralino-target cross section from the data, one
has the inequality
σ
SD
χN
≤ σ
SDlim
χN
. (10.64)
So, one can define a limit on the neutralino-proton cross section, σ
SDlim
p
correspon-
ding to the neutralino–nucleus N cross section limit σ
SDlim
χN
as
σ
SDlim
p
= σ
SDlim
χN
µ
2
χp
µ
2
χN
C
p
SD
C
p(N)
SD
(10.65)
and, analogously, for neutrons
σ
SDlim
n
= σ
SDlim
χN
µ
2
χn
µ
2
χN
C
n
SD
C
n(N)
SD
(10.66)
with (one assumes the same mass for proton and neutron):
µ
2
χN
µ
2
χp
=
µ
2
χN
µ
2
χn
·
1 + m
χ
/m
p
1 + m
χ
/m
N
¸
2
. (10.67)
Equations (10.65) and (10.66) allows the calculation of the exclusion limits on the
neutralino-proton and neutralino-neutron cross sections as a function of the neu-
tralino mass.
Coming back to Eq. (10.54), σ
SD
χN
(0) can be expressed as
σ
SD
χN
(0) =
µ
q
σ
p
SD
κ
p
±
p
σ
n
SD
κ
n
¶
2
, (10.68)
January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
746 Principles of Radiation Interaction in Matter and Detection
where one has defined
κ
p
=
µ
2
χN
µ
2
χp
C
p(N)
SD
C
p
SD
(10.69)
and
κ
n
=
µ
2
χN
µ
2
χp
C
n(N)
SD
C
n
SD
. (10.70)
Then, it follows
1 =
Ã
s
σ
p
SD
κ
p
σ
SD
χN
±
s
σ
n
SD
κ
n
σ
SD
χN
!
2
. (10.71)
Using the inequality of Eq. (10.64), one has
1 ≥
Ã
s
σ
p
SD
κ
p
σ
SDlim
χN
±
s
σ
n
SD
κ
n
σ
SDlim
χN
!
2
. (10.72)
Since
κ
p
σ
SDlim
χN
=
1
σ
p
SDlim
(10.73)
and
κ
n
σ
SDlim
χN
=
1
σ
n
SDlim
, (10.74)
then Eq. (10.72) becomes
1 ≥
s
σ
p
SD
σ
p
SDlim
±
s
σ
n
SD
σ
n
SDlim
2
. (10.75)
If one considers one isolated proton (J = 1/2, hS
p
i = 1/2), one finds
C
SD
p
=
8
π
(J + 1)
J
a
2
p
hS
p
i
2
=
6
π
a
p
2
(10.76)
and [via Eq. (10.56)]
σ
SD
p
= 4G
F
2
µ
2
χp
6
π
a
p
2
=
24
π
G
F
2
µ
2
χp
a
p
2
. (10.77)
For an isolated neutron (J = 1/2, hS
n
i = 1/2), we obtain
C
SD
n
=
8
π
(J + 1)
J
a
2
n
hS
n
i
2
=
6
π
a
n
2
(10.78)
and [via Eq. (10.56)]
σ
SD
n
= 4G
F
2
µ
2
χp
6
π
a
p
2
=
24
π
G
F
2
µ
2
χp
a
n
2
. (10.79)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Superheated Droplet (Bubble) Detectors and CDM Search 747
Introducing Eqs. (10.77, 10.79) in Eq. (10.75), one finds
π
24G
F
2
µ
χp
2
≥
Ã
a
p
p
σ
p
SDlim
±
a
n
p
σ
n
SDlim
!
2
. (10.80)
The limit represents an allowed band in the a
p
/a
n
plane. The sign of the slop e is
determined by the sign appearing in parentheses in Eq. (10.80). This latter sign is
determined by the sign of the ratio hS
p
i/ hS
n
i. The optimal limit on the a
p
and a
n
couplings could be obtained by using two target nuclei having hS
p
i/ hS
n
i ratios of
opposite signs. The allowed region should then be comprised within the intersection
of the two bands with slopes of opposite signs [Tovey et al. (2000)]. An example of
limits calculation in the a
p
/a
n
plane will be given later for the PICASSO experiment
(Sect. 10.2.2).
10.2.1.3 Calculation of hS
p
i and hS
n
i in Nuclei
The total enhancement factor, C
SD
N
, in the spin-dependent neutralino–nucleus ela-
stic cross section has been defined previously as
C
SD
N
=
8
π
(a
p
hS
p
i + a
n
hS
n
i)
2
J + 1
J
, (10.81)
where a
p
and a
n
are effective χ–proton and χ–neutron couplings; J is the total
nuclear spin and hS
p
i = hN|S
p
|Ni and hS
n
i=hN|S
n
|Ni are the expectation values
of the proton and neutron spins within the nucleus.
In the case of free nucleons hS
p
i = 0.5 and hS
n
i = 0.5, obviously, and the
corresponding enhancement factors are C
p
= (6/π) a
2
p
and C
n
= (6/π) a
2
n
.
In the case of nuclei, the calculation of hS
p
i and hS
n
i depends on the nuclear
model. The calculation p erformed in three models are presented: the extreme
single-particle model (ESPM)([Engel and Vogel (1989)]), the odd-group model
(OGM)([Engel and Vogel (1989)]) and the extended odd-group model (EOGM)
([Engel and Vogel (1989)]). The odd-group model uses the measured nuclear mag-
netic moment to obtain hS
p
i and hS
n
i. The extended odd-group model uses the
measured nuclear magnetic moment and the ft-value for the Gamow-Teller β-decay,
leading to more realistic predictions for hS
p
i and hS
n
i. Finally, the nuclear angular
moment and the nuclear magnetic moment can be calculated from the values of
hS
p
i and hS
n
i obtained from shell models. Comparison is done with the experi-
mental nuclear magnetic moment for several nuclei. One turns now to the detailed
calculation of hS
p
i and hS
n
i.
Assuming charge symmetry of nuclear forces, the magnetic moments of the odd-
proton (µ
p
) and odd-neutron (µ
n
) members of a mirror pair are [Buck and Perez
(1983)]:
µ
p
= g
p
L
o
+ G
p
S
o
+ g
n
L
e
+ G
n
S
e
(10.82)
and
µ
n
= g
n
L
o
+ G
n
S
o
+ g
p
L
e
+ G
p
S
e
, (10.83)

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
748 Principles of Radiation Interaction in Matter and Detection
Table 10.2 Test of hS
p
i and hS
n
i calculated from shell models; “small” and “large” refer to the size of model spaces which adequately describe
the configuration mixings in the nuclei [Ressell et al. (1993)].
Nucleus J S
p
S
n
L
p
L
n
J Ref. µ µ
exp
[Eq. (10.105)] [Eq. (10.106)]
19
F 1/2 0.4751 -0.0087 0.2235 -0.1899 0.50 [Divari et al. (2000)] 2.911 2.629
29
Si 1/2 -0.0019 0.1334 0.0183 0.3498 0.499(6) [Divari et al. (2000)] -0.503 -0.555
23
Na 3/2 0.2477 0.0199 0.9115 0.3207 1.499(8) [Divari et al. (2000)] 2.219 2.218
73
Ge 9/2 0.030 0.378 0.361 3.732 4.501 [Dimitrov, Engel and Pittel (1995)] -0.918 -0.879
73
Ge 9/2 0.005 0.496 0.40 3.596 4.497 [Ressell et al. (1993)]-“small” -1.470 -0.879
73
Ge 9/2 0.011 0.468 0.491 3.529 4.499 [Ressell et al. (1993)]-“large” -1.238 -0.879

January 9, 2009 10:21 World Scientific Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed
Superheated Droplet (Bubble) Detectors and CDM Search 749
where g
p
= 1, G
p
= 5.586, g
n
= 0 and G
n
= −3.826 (all in nuclear magnetons
units) are the orbital g and spin G factors for proton and neutron. The odd- and
even-nucleon contributions to the angular moment are labeled by the subscripts “o”
and “e”, respectively. For both nuclei, the total angular moment J is equal to:
J = L
o
+ S
o
+ L
e
+ S
e
(10.84)
and
J
e
= L
e
+ S
e
, (10.85)
where S
i
and L
i
(i = o, e) are the nuclear spin and orbital moment components,
respectively. Equations (10.84) and (10.85) allow one to rewrite Eqs. (10.82, 10.83)
as
µ
p
= g
p
L
o
+ G
p
S
o
+ g
n
(J − L
o
− S
o
− S
e
) + G
n
S
e
= g
p
J + (G
p
− g
p
) (S
o
− S
e
) − (g
p
− g
n
) J
e
+ (G
p
− g
p
+ G
n
− g
n
) S
e
(10.86)
and
µ
n
= g
n
L
o
+ G
n
S
o
+ g
p
(J − L
o
− S
o
− S
e
) + G
p
S
e
= g
n
J + (G
n
− g
n
) (S
o
− S
e
) + (g
p
− g
n
) J
e
+ (G
p
− g
p
+ G
n
− g
n
) S
e
. (10.87)
If even-nucleon contributions are neglected in Eqs. (10.86, 10.87), one finds:
µ
p
≈ g
p
J + (G
p
− g
p
)S
o
, (10.88)
giving
S
o
=
µ
p
− g
p
J
(G
p
− g
p
)
, (10.89)
and
µ
n
≈ g
n
J + (G
n
− g
n
)S
o
, (10.90)
giving
S
o
=
µ
n
− g
n
J
(G
n
− g
n
)
. (10.91)
Equations (10.89, 10.91) are the odd-group model (OGM) expressions in which
the odd-nucleon spin is related to the nuclear magnetic moment µ and the gyromag-
netic factors G
p,n
and g
p,n
. They allow the calculation of S
o
using the experimental
magnetic moment. For instance,
19
F is an odd-proton nucleus with J = 1/2, a S
1/2
state, and with µ
exp
= 2.629. Therefore, Eq. (10.89) gives the value:
hS
p
i = S
o
= [2.629 − 1.0 × (1/2)] /(5.586 − 1.0) = 0.46,
hS
n
i = 0
(10.92)
