Лекции по теории передачи информации

Подождите немного. Документ загружается.

щем сообщении, иначе при кодировании будут происходить потери в переда-

ваемой информации. Во-вторых, кодирование будет тем более эффективным,

чем большее количество информации будет содержать в себе каждый кодовый

символ. Это количество информации максимально, когда все кодовые символы

равновероятны, и равно .

При этом i-е кодовое слово будет нести количе-

ство информации, равное

log

.log m

Шенноном сформулирована следующая теорема. При кодировании сооб-

щений

в алфавите, насчитывающем m символов, при условии отсутствия

шумов, средняя длина кодового слова не может быть меньше, чем

,)log( m

L ≥

(6.2)

где H(X) – энтропия сообщения.

Если вероятности сообщений не являются целочисленными степенями

числа

m, точное достижение указанной границы невозможно, но при кодирова-

нии достаточно длинными группами к этой границе можно сколь угодно при-

близиться.

Данная теорема не дает явных рецептов для нахождения кодовых слов со

средней длиной (6.2), а поэтому она является теоремой существования. Важ-

ность этой теоремы состоит в том, что она определяет предельно

возможную

эффективность кода, позволяет оценить, насколько тот или иной конкретный

код близок к самому экономному, и, наконец, придает прямой физический

смысл одному из основных понятий теории информации – энтропии множества

сообщений как минимальному числу двоичных символов (

m = 2), приходящих-

ся в среднем на одно сообщение.

Приведем два известных способа построения кодов, которые позволяют

приблизиться к равновероятности и независимости кодовых символов.

6.1.1. Код Шеннона-Фано. Для построения этого кода все сообщения X

вы-

писываются в порядке убывания их вероятностей (табл. 6.1).

Таблица 6.1

Построение кода Шеннона-Фано

P(x

)

Разбиение сообщений на

подгруппы

Код

0,35 1 1 1 1 2 0,70

0,15 1 0 1 0 2 0,30

0,13 0 1 1 0 1 1 3 0,39

0,09 0 1 0 0 1 0 3 0,27

0,09 0 0 1 1 0 0 1 1 4 0,36

0,08 0 0 1 0 1 0 0 1 0 4 0,32

0,05 0 0 0 0 1 0 0 0 1 4 0,20

0,04 0 0 0 0 1 0 0 0 0 1 5 0,20

0,02 0 0 0 0 0 0 0 0 0 0 5 0,10

Записанные таким образом сообщения затем разбиваются на две по воз-

можности равновероятностные подгруппы. Всем сообщениям первой подгруп-

пы присваивают цифру 1 в качестве первого кодового символа, а сообщениям

второй подгруппы – цифру 0. Аналогичное деление на подгруппы продолжает-

ся до тех пор, пока в каждую подгруппу не попадает по одному сообщению.

Найденный код весьма

близок к оптимальному. В самом деле, энтропия

сообщений:

собщение

бит

)(log

)()(

75,2)02,0log02,004,0log04,0

05,0log05,008,0log08,009,0log09,009,0log09,0

13,0log13,015,0log15,035,0log35,0(

≅++

+++++

+++−

∑

−=

PPXH

(6.3)

Средняя длина кодового слова:

.84,210,020,020,032,036,027,039,030,070,0

=++++++++=

∑

(6.4)

Среднее число нулей:

29,110,016,015,024,018,018,013,015,0)0(

. (6.5)

Среднее число единиц:

.55,104,005,008,018,009,026,015,070,0)1(

+++=

(6.6)

Вероятность появления нулей:

.455,0

84,2

29,1

)0(

)0( ===

(6.7)

Вероятность появления единиц

.545,0

84,2

55,1

)1(

)1( ===

(6.8)

Таким образом, получили код близкий к оптимальному.

6.1.2. Код Хаффмана. Для получения кода Хаффмана все сообщения выпи-

сывают в порядке убывания вероятностей. Две наименьшие вероятности объе-

диняют скобкой (табл. 6.2) и одной из них присваивают символ 1, а дру-

гой – 0.

Затем эти вероятности складывают, результат записывают в промежутке

между ближайшими вероятностями. Процесс объединения двух сообщений с

наименьшими вероятностями продолжают до тех пор, пока

суммарная вероят-

ность двух оставшихся сообщений не станет равной единице. Код для каждого

сообщения строится при записи двоичного числа справа налево путем обхода

по линиям вверх направо, начиная с вероятности сообщения, для которого

строится код.

Средняя длина кодового слова (табл. 6.2)

L = 2,82, что несколько меньше,

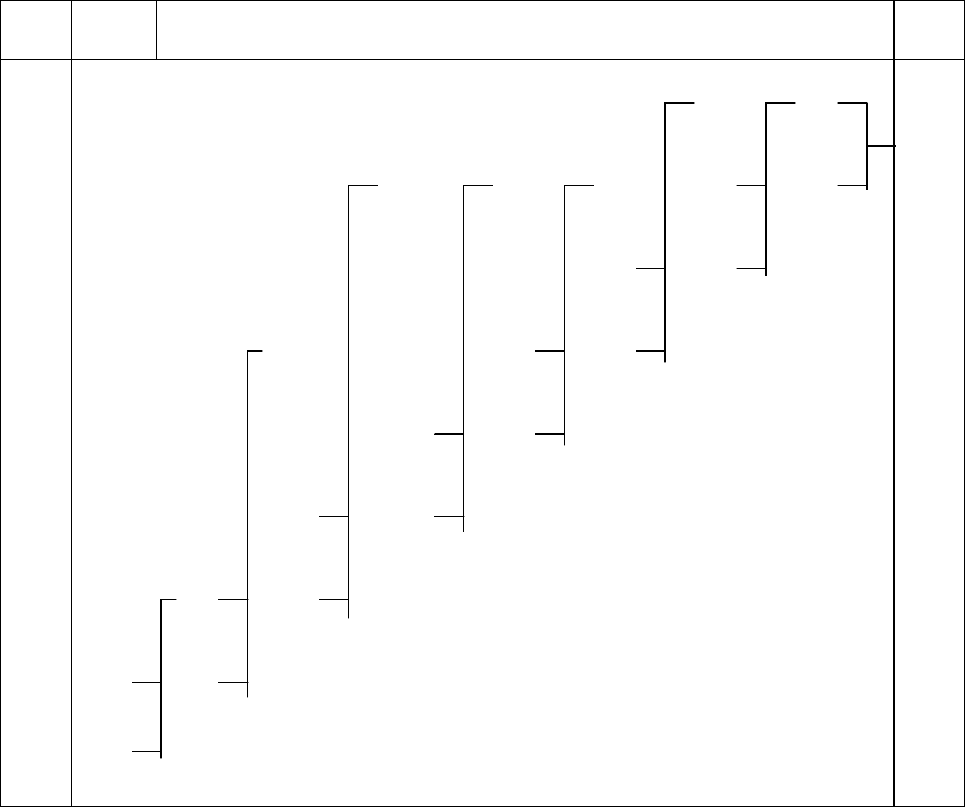
чем в коде Шеннона-Фано (L = 2,84). Кроме того, методика Шеннона-Фано не

всегда приводит к однозначному построению кода. Ведь при разбиении на под-

группы можно сделать большей по вероятности как верхнюю, так и нижнюю

подгруппы. От этого недостатка свободна методика Хаффмана. Она гарантиру-

ет однозначное построение кода с наименьшим для данного распределения ве-

роятностей средним числом

символов на букву. Однако, как следует из приве-

денных выше цифр, некоторая избыточность в кодовых комбинациях осталась.

Из теоремы Шеннона следует, что эту избыточность также можно устранить,

если перейти к кодированию достаточно большими блоками.

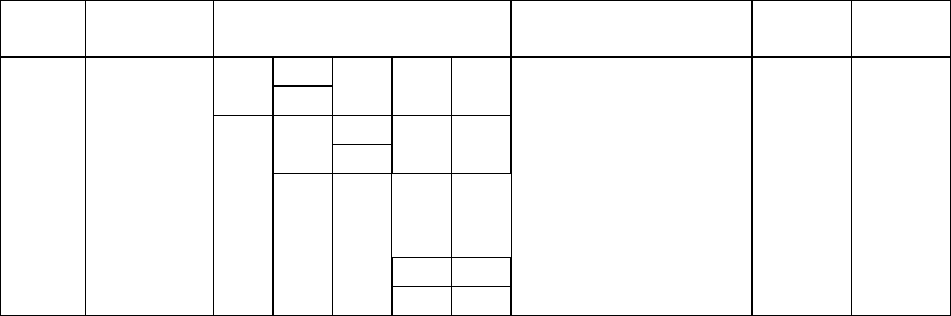
Таблица 6.2

Построение кода Хаффмана

P(X

)

Объединение сообщений Код

0,35

0,37

0,63

0,15

0,17

0,20

0,28

0,35

0,37

101

0,13

0,15

0,17

0,20

0,28

100

0,09

0,11

0,13

0,15

0,17

010

0,09

0,11

0,13

001

0,08

0,09

000

0,05

0,06

0,08

0110

0,04

0,05

0111

0,02

0111

Рассмотрим процедуру эффективного кодирования двух сообщений

и X

с вероятностями

P(X

) = 0,9 и P(X

) = 0,1 по методу Хаффмана: отдельных со-

общений; сообщений, составленных по два в группе; сообщений, составленных

по три в группе. Сравним коды по эффективности

L , по скорости передачи R

по избыточности R, если длительности кодовых символов одинаковы и равны

−

=τ

Энтропия источника в соответствии с (1.14)

сообщение

бит

469,01,0log1,09,0log9,0)( =−−=XH

(6.8)

При кодировании отдельных сообщений методом Хаффмана сообщению

сопоставляется кодовый символ 1, а сообщению X

– 0. Средняя длина кодо-

вого символа при этом:

.111,019,0

⋅

(6.9)

Скорость передачи:

бит

469000

469,0

)(

===

−

(6.10)

что составляет 46,9% от пропускной способности

Избыточность кода

равна избыточности источника сообщений:

.531,0

469,01

)max(

)()max(

−

XHXH

Для повышения эффективности кода перейдем к кодированию групп со-

общений (табл. 6.3).

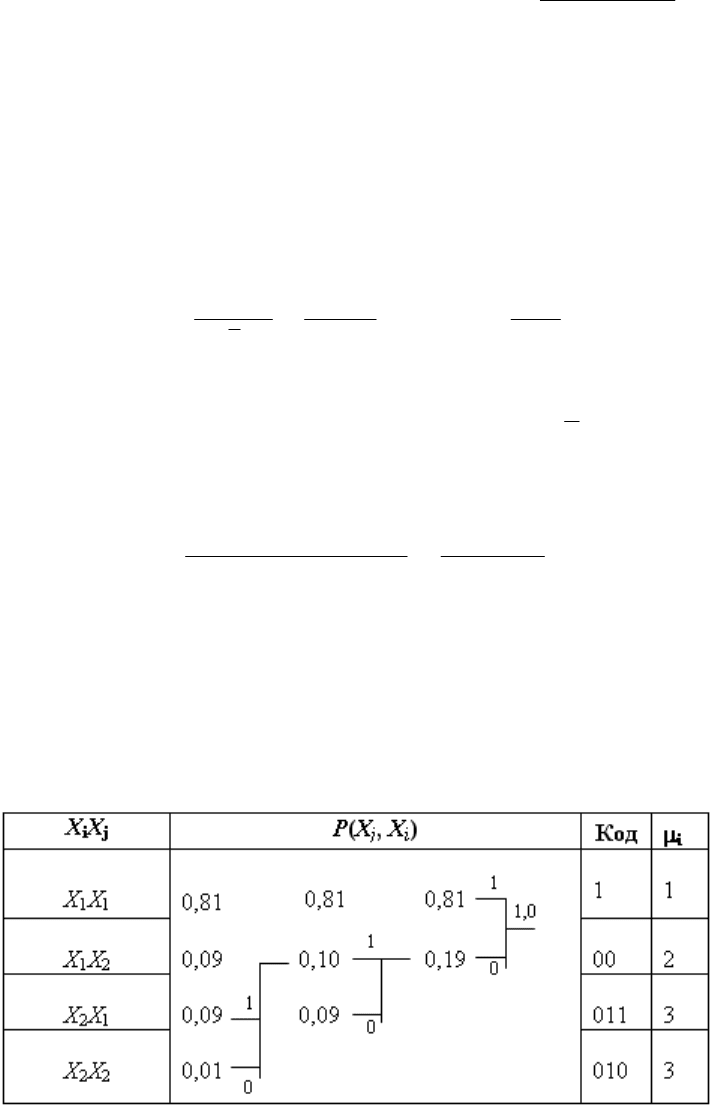
Таблица 6.3

Кодирование сообщений, составленных по два в группе

Средняя длина кодового слова, приходящего на одно сообщение:

.645,0)01,0309,0309,0281,01(2

1 =

⋅

⋅⋅

(6.11)

Скорость передачи при этом

727000

10645,0

469,0

)(

бит

⋅

−

(6.12)

что составляет 72,7% от максимально возможной скорости передачи

(10

бит/с).

Чтобы найти избыточность кода, вычислим вероятность появления кодо-

вого символа 0 и 1:

.77,0)0(1)1(

.23,0

)645,02(

)01,0209,0209,0(

)0(

=−=

⋅

Энтропия кода:

символ

бит

778,077,0log77,023.0log23,0 =−−=

Избыточность:

= 1 – H

= 0,222.

А сейчас перейдем к кодированию групп сообщений, содержащих три со-

общения в группе (табл. 6.4).

Средняя длина кодового слова, приходящаяся на одно сообщение, в этом

случае будет:

.533,0)5001,015009,09081,0729,0(3

1 =

⋅

При этом скорость передачи:

бит

880000

10533,0

469,0

⋅

−

что составляет 88% от пропускной способности.

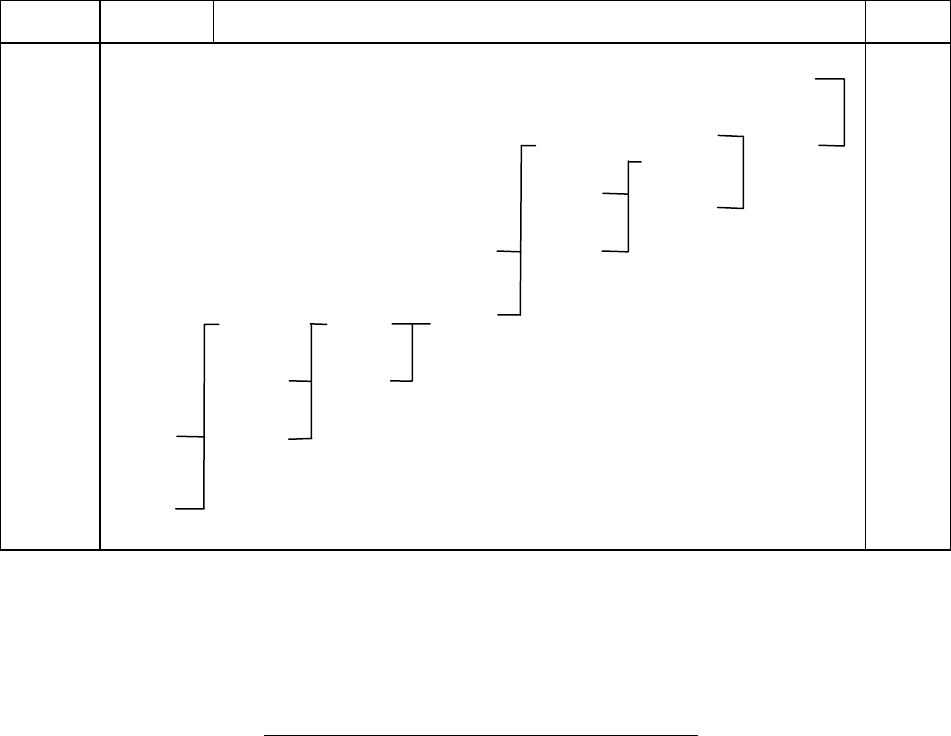
Таблица 6.4

Кодирование сообщений, составленных по три в группе

P(X

) Объединение сообщений Код

0,729

0,729 0,729 0,729 0,729 0,729 0,729

0,081

0,081 0,081 0,081 0,109 0,162 0,271

011

0,081

0,081 0,081 0,081 0,081 0,109

010

0,081

0,081 0,081 0,081 0,081

001

0,009

0,010 0,018 0,028

00011

0,009

0,009 0,010

00010

0,009

00001

0,001

00000

Вероятность появления символов 0 и 1:

.68,0)0(1)1(

;32,0

3533,0

)5001,011009,05081,0(

)0(

=−=

⋅

Найдем энтропию и избыточность кода в этом случае:

.096,01

904,068,0log68,032,0log32,0

;

=−=

−

−=

Сведем полученные результаты в табл. 6.5.

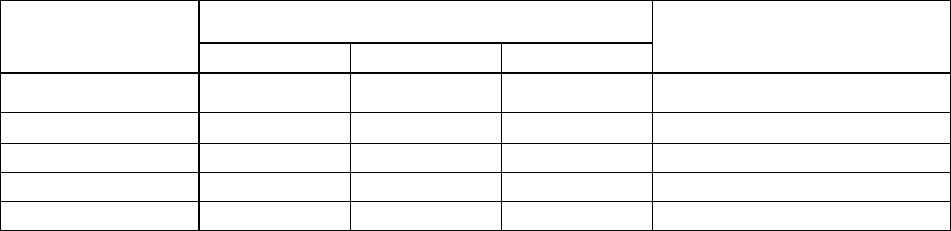
Таблица 6.5

Результаты, полученные при кодировании

Число сообщений в группе

Вычисляемые

величины

1 2 3

Предельные значения вы-

числяемой величины

1 0,645 0,533 H(X)/log2 = 0,469

бит/с

469000 727000 880000

C =1/τ = 10

-6

P(0) 0,9 0,23 0,32 P(0) = 0,5

P(1) 0,1 0,77 0,68 P(1) = 0,5

, % 53,1 23.2 9,6 R

= 0

Если кодировать группы по 4 и более сообщений, мы еще более прибли-

зимся к предельным значениям вычисляемых величин.

Следует подчеркнуть, что увеличение эффективности кодирования при ук-

рупнении блоков не связано с учетом все более далеких систематических свя-

зей, так как нами рассматривались алфавиты с некоррелированными знаками.

Повышение эффективности определяется лишь тем, что

набор вероятностей,

получающихся при укрупнении блоков

, можно делить на более близкие по

суммарным вероятностям подгруппы.

6.2. Префиксные коды

Рассмотрев методики построения эффективных кодов, нетрудно убе-

диться в том, что эффект достигается благодаря присвоению более коротких

кодовых комбинаций более вероятным сообщениям и более длинных менее ве-

роятным сообщениям. Таким образом, эффект связан с различием в числе сим-

волов кодовых комбинаций. А это приводит к трудностям при декодировании.

Конечно, для

различения кодовых комбинаций можно ставить специальный

разделительный символ, но при этом значительно снижается эффект, которого

мы добивались, так как средняя длина кодовой комбинации по существу увели-

чивается на символ.

Более целесообразно обеспечить однозначное декодирование без введе-

ния дополнительных символов. Для этого эффективный код необходимо стро-

ить так, чтобы ни одна комбинация

кода не совпадала с началом более длинной

комбинации. Коды, удовлетворяющие этому условию, называют префиксными

кодами. Последовательность 100000110110110100 комбинаций префиксного

кода, например,

1001010100

4321

XXXX

декодируется однозначно:

1333214

001011011010100100

XXXXXXX

Последовательность 000101010101 комбинаций непрефиксного кода, на-

пример,

0101010100

4321

XXXX

(комбинация 01 является началом комбинации 010), может быть декодирована

по-разному:

342221

10101001010100

XXXXXX

34341

10101010101000

XXXXX

223421

01011010100100

XXXXXX

Нетрудно убедиться, что коды, получаемые в результате применения ме-

тодики Шеннона-Фано или Хаффмана, являются префиксными.

6.3. Недостатки системы эффективного кодирования

Причиной одного из недостатков является различие в длине кодовых

комбинаций. Если моменты снятия информации с источника неуправляемы,

кодирующее устройство через равные промежутки времени выдает комбинации

различной длины. Так как линия связи используется эффективно только в том

случае, когда символы поступают в нее с постоянной скоростью, то на выходе

кодирующего устройства

должно быть предусмотрено буферное устройство.

Оно запасает символы по мере поступления и выдает их в линию связи с посто-

янной скоростью. Аналогичное устройство необходимо и на приемной стороне.

Второй недостаток связан с возникновением задержки в передаче инфор-

мации.

Наибольший эффект достигается при кодировании длинными блоками, а

это приводит к необходимости накапливать

знаки, прежде чем поставить им в

соответствие определенную последовательность символов. При декодировании

задержка возникает снова. Общее время задержки может быть велико, особенно

при появлении блока, вероятность которого мала. Это следует учитывать при

выборе длины кодируемого блока.

Еще один недостаток заключается в специфическом влиянии помех на

достоверность приема. Одиночная ошибка может перевести передаваемую ко-

довую комбинацию в другую, не равную ей по длительности. Это повлечет за

собой неправильное декодирование ряда последующих комбинаций, которые

называют

треком ошибки.

Специальными методами построения эффективного кода трек ошибки

стараются свести к минимуму.

Следует отметить относительную сложность технической реализации

систем эффективного кодирования.

Методы эффективного кодирования Шеннона-Фано и Хаффмана, рас-

смотренные выше, позволяют производить кодирование, если известна стати-

стика входных сообщений, т.е. известна вероятность их появления

p(x

6.4. Эффективное кодирование при неизвестной

статистике сообщений

Коды, эффективные одновременно для некоторого класса источников, на-

зывают универсальными кодами. Сформулируем постановку задачи универ-

сального кодирования источников. Предположим, что алфавит состоит из двух

и X

, появляющихся независимо, с вероятностями p и g = 1-p. Однако вели-

чина

р заранее неизвестна. Требуется построить код, для которого среднее чис-

ло символов «0» и «1» на одну букву алфавита приближалось бы к

H(X) при

любом

р, 10 <=<=

. Этот код строится так. Множество всех блоков длины n в

алфавите X разбиваем на группы, которые имеют одинаковые вероятности при

любом

p. Таких групп будет n+1. В нулевой группе отсутствует буква X

, она

состоит из единственного блока

…X

, вероятность появления которого

. Первая группа состоит из блоков длиной n, содержащих одну букву X

. Эта

группа состоит из

= n блоков, вероятность каждого из которых равна

. Группы с номером k состоят из всех блоков длиной n, содержащих k

букв

⋅

− 1

. Эта группа содержит n блоков, вероятность каждого из кото-

рых

kkn

⋅

−

Универсальный код для

k-й группы состоит из двух частей: префикса и

суффикса. Префикс содержит log(

n+1) двоичных знаков. Префикс указывает, к

какой группе сообщений принадлежит кодируемый блок, суффикс содержит

двоичных символов и указывает номер блока в группе.

log

Построенный таким образом код будет однозначно дешифрируем. На

приемном конце первоначально по log(

n+1) элементам кода определяют, к ка-

кой группе принадлежит переданное сообщение, а затем по следующим

элементам определяют, какое именно сообщение передавалось.

log

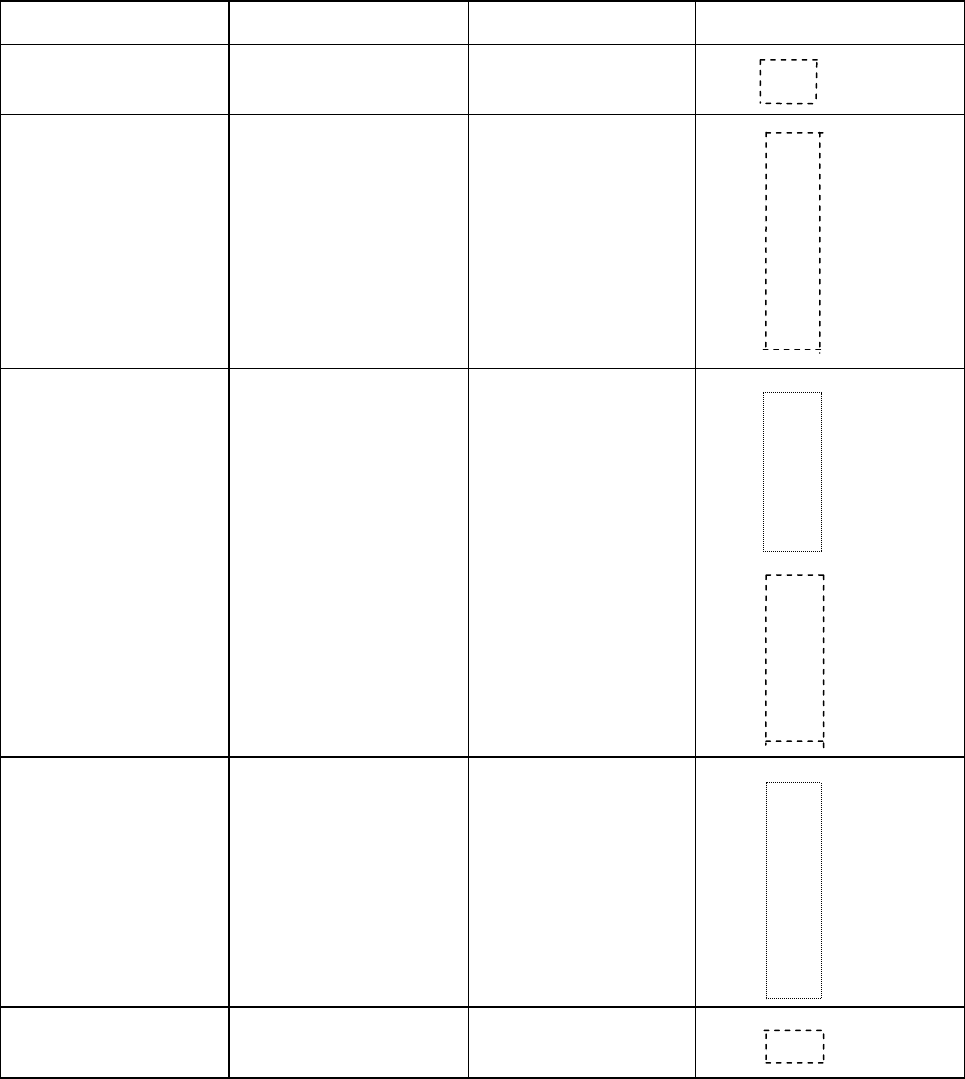
Код в табл. 6.6 построен описанным выше способом. Здесь выделены

штриховой линией префиксы.

Таблица 6.6

Построение префиксного кода

Кодируемые слова Номер группы Вероятность слова Код

000

001 00

001 01

001 10

001 11

010 000

010 001

010 010

010 011

010 100

010 101

011 00

Рg

011 01

011 10

011 11

100

Из приведенного выше описания метода кодирования видно, что наиболее

трудоемкой частью кодирования является нахождение суффикса. Опишем ал-

горитм нахождения суффикса. Пусть в блоке

X длиной n буква X

встречается