Лекции по теории передачи информации

Подождите немного. Документ загружается.

2. ИСТОЧНИКИ ДИСКРЕТНЫХ СООБЩЕНИЙ

2.1. Энтропия эргодического источника

Достаточно хорошей математической моделью дискретных источников,

встречающихся на практике, являются так называемые эргодические источни-

ки. Назовём эргодическим источником r-го порядка такой источник, у которого

вероятность появления некоторого символа x

зависит от r предыдущих. Для та-

кого источника может быть найдено конечное число характерных состояний S

,..., таких, что условная вероятность появления очередного символа зависит

лишь от того, в каком из этих состояний находится источник. Вырабатывая

очередной символ, источник переходит из одного состояния в другое либо воз-

вращается в исходное состояние.

Определим энтропию эргодического источника в предположении, что он

работает длительное время и, всякий раз, когда мы

ждём появления очередного

символа, нам известно, какие символы были выбраны ранее, и, следовательно,

известно, в каком характерном состоянии находится источник.

Обозначим через P(S

) вероятность того, что источник находится в состоя-

нии S

, причём

(2.1)

∑

.1)(

Предположим, мы установили, что источник находится в состоянии S

. У

нас имеется неопределённость, из какого состояния S

источник, выработав не-

который символ, перешёл в состояние S

. Так как вероятность состояния S

за-

висит только от предыдущего состояния S

и не зависит от того, в каких со-

стояниях находился источник ранее, неопределённость источника в состоянии

можно найти по формуле, аналогичной (1.14):

)./(log)/()(

kbk

SSPSSPSH

∑

−

(2.2)

Величина H(S

) случайно меняется в зависимости от состояния источника,

поэтому только среднее значение H(S

) может характеризовать энтропию ис-

точника:

∑∑

∑

−

kbkb

kkkb

kbkbkkk

SSPSSP

SSPSSPSPSHSPXH

),/(log),(

)/(log)/()()()()(

(2.3)

где значок b/k у суммы означает, что производится суммирование по всем пере-

ходам из состояния S

в S

Таким образом, энтропия Н(Х) есть среднее значение (математическое

ожидание) энтропий всех характерных состояний источника.

В случае, когда символы источника независимы, имеется лишь одно со-

стояние S

, вероятность которого P(S

) = 1. При появлении символа x

источник

вновь возвращается в состояние S

(рис. 2.1), и при этом P(S

) = P(x

), следо-

вательно,

),(log)()()(

1 i

xPxPSHXH

∑

−==

что совпадает с (1.14).

Если коррелятивные связи имеются между двумя соседними символами, то

P(S

) = P(x

) и P(S

) = P(x

Из (2.3) тогда получим

символ

дв.ед.

)/(log),(

)/(log)/()()(

kbk

xxPxxP

xxPxxPxPXH

∑∑

−=

=−=

(2.4)

Источник, генерирующий n разных символов – x

...

, в этом случае

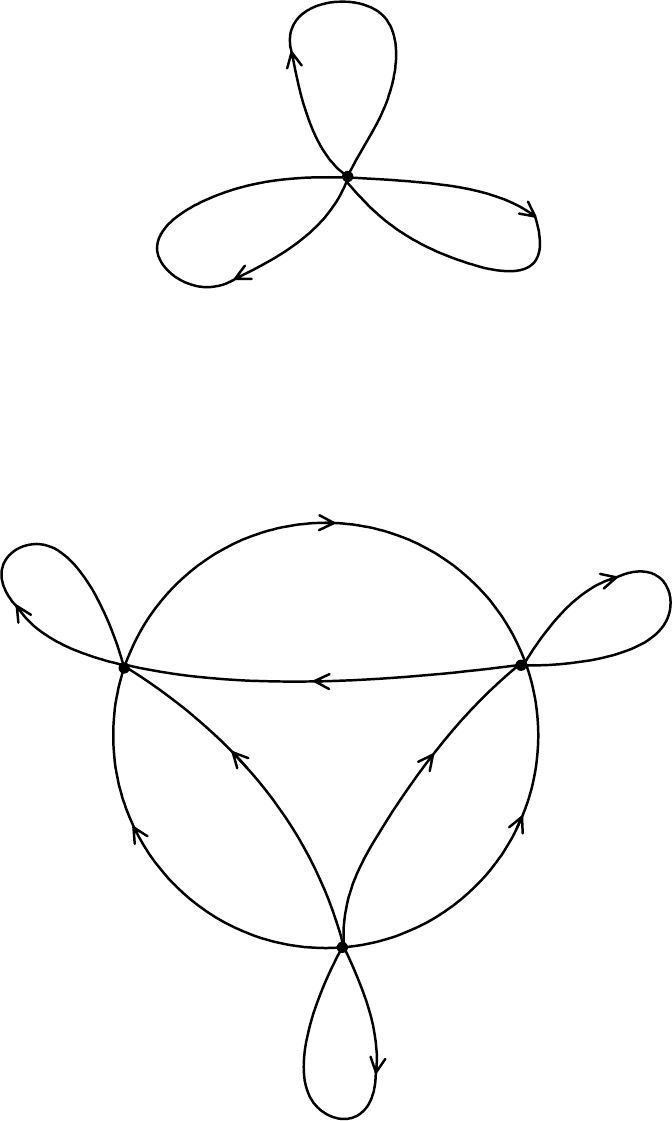
может иметь n характерных состояний. Пример такого источника для случая

3 приведён на рис. 2.2.

В случае когда коррелятивные связи имеются между тремя символами, ха-

рактерные состояния определяются передачей двух символов, и их удобно ну-

меровать двумя индексами. Так, если генерируются x

, то источник переходит

в состояние S

и тогда:

P(S

) = P(x

) и P(S

) = P(x

) .

Из (2.4) получаем

символ

дв.ед.

),/(log),,(

),/(log),/(),()(

111

jhi

xxxPxxxP

xxxPxxxPxxPXH

∑∑∑

===

(2.5)

Чисел характерных состояний для этого случая столько, сколько имеется

различных пар (x

). Таких пар, очевидно, n

Аналогичные соотношения получаются и в случае, когда коррелятивные

связи распространяются на большее число символов.

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

P(x

)

Рис. 2.1. Диаграмма перехода, когда источник имеет

одно характерное состояние

Рис. 2.2. Диаграмма перехода, когда источник имеет

три характерных состояния

2.2. Свойство энтропии эргодических источников

Теорема 1. Для любых и 00>ε >

можно найти такое M

, при котором

эргодические последовательности с длиной

распадаются на два клас-

са:

MM >

1) типичные, вероятности которых удовлетворяют следующему неравенст-

ву:

)(

log

)( δ<−

(2.6)

где Н(Х) – энтропия эргодического источника;

2) нетипичные, сумма вероятностей которых меньше ε.

Доказательство. Последовательность C длины M образуется в результате

поочередного перехода источника из одного характерного состояния в другое.

Рассмотрим переход из состояния S

в состояние S

во множестве последо-

вательностей С. Число M всегда может быть выбрано настолько большим, что

сумма вероятностей всех нетипичных последовательностей меньше ε. Учиты-

вая, что для типичной последовательности частота событий может быть как

угодно близка к их вероятности, можно утверждать, что в каждой типичной по-

следовательности источник пребывает в состоянии S

приблизительно M

)

раз, а число переходов из состояния S

в состояние S

приблизительно равно

) P(S

), а точнее

M(P(S

) P(S

) ± η ), (2.7)

где η с увеличением M может быть сделано как угодно малым.

Вероятность того, что в рассматриваемой последовательности имеет место

М переходов из состояния S

в S

, равна по теореме умножения вероятностей

.)/(

))/()((

kbk

SSPSPM

SSP

(2.8)

Вероятность появления конкретной последовательности С определяется

как вероятность всех возможных переходов, и, следовательно,

.)/()(

))/()((

∏∏

kbk

SSPSPM

kkb

SSPCP

(2.9)

Логарифмируя последнее равенство, получаем:

)/log()/(log)/()(

)(

log

kkb

bkbk

kkb

SSSSPSSPSP

∑∑∑∑

η±−= . (2.10)

Если учесть, что первая сумма в правой части совпадает с (2.3), а вторая

вследствие произвольной малости η всегда может быть меньше δ, то получим

неопределённость (2.6).

Следствие 1. Типичные последовательности приблизительно равноверо-

ятны.

Для доказательства из (2.6) найдём Р(С):

.2)(2

)()( δ−−δ+−

HMHM

При .0, →δ∞→

Поэтому при достаточно большом М можно положить

P(C) ≈ 2

-MH(X)

(2.11)

Из (2.11) видно, что все последовательности С равновероятны и число их

= 2

MH(X)

. (2.12)

В случае, если все n символов источника независимы и равновероятны, то

= 2

Mlogn

= n

. (2.13)

Легко видеть, что (2.13) определяет число всех возможных последователь-

ностей длины М, содержащих n различных символов.

Следствие 2. Чтобы экспериментально определить энтропию эргодиче-

ского источника, у которого вероятностные связи распространяются на очень

большое число символов, нам необходимо располагать последовательностью

ещё большей длины (

); при этом вычисленная энтропия будет как угодно

близка к своему пределу log1/P(C) = H(X).

2.3. Избыточность источника сообщений

Как известно, энтропия характеризует среднее количество информации,

несомое одним символом источника. Она максимальна, когда символы выраба-

тываются источником с равной вероятностью. Если же некоторые символы по-

являются чаще других, энтропия уменьшается, а при появлении дополнитель-

ных вероятностных связей между символами становится ещё меньше. Чем

меньше энтропия источника отличается от максимальной,

тем рациональнее он

работает, тем большее количество информации несут его символы.

Для сравнения источников по их информативности введём параметр, назы-

ваемый избыточностью, равный

)(

)()(

max

XHXH

−

(2.14)

Источник, избыточность которого R = 0, называется оптимальным. Если

1, то Н(Х) = 0, и, следовательно, информация, вырабатываемая источником,

равна нулю. В общем случае .10

≤

Чем меньше избыточность R, тем ра-

циональнее работает источник.

Следует, однако, иметь в виду, что не всегда нужно стремиться к тому,

чтобы R = 0. Некоторая избыточность бывает полезной для обеспечения надеж-

ности передачи сообщений. Простейшим видом введения избыточности для

борьбы с шумами является многократная передача одного и того же символа.

2.4. Поток информации источника сообщений

При работе источника сообщений на его выходе отдельные символы появ-

ляются через некоторые интервалы времени; в этом смысле мы можем говорить

о длительности отдельных символов, и, следовательно, может быть поставлен

вопрос о количестве информации, вырабатываемой источником в единицу вре-

мени.

Длительность выдачи знаков источником в каждом состоянии в общем

случае

может быть различной. Тогда средняя длительность выдачи источником

одного знака:

,)()(

∑

xPSP

(2.15)

где P(S

) – вероятность того, что источник сообщений находится в состоянии

; P(x

) – вероятность появления символа x

в состоянии S

; τ

– длительность

выдачи знака x

источником в состоянии S

Энтропия источника, приходящаяся на единицу времени, может быть на-

звана скоростью создания сообщений, или потоком информации, т.е.

дв.ед.)(

)(

XH =

(2.16)

Если длительность выдачи знака не зависит от состояния источника, для

всех знаков одинакова и равна

то

Выражение для

)( XH

принимает

вид:

дв.ед.)(

)(

XH =

(2.17)

В этом случае поток информации максимальный, если энтропия источника

на символ максимальна. Для увеличения потока информации необходимо по

возможности уменьшить среднюю длительность символов

. С этой целью, на-

пример, необходимо, чтобы длительность тех символов, вероятность появления

которых больше, была меньше, чем для символов, вероятность появления кото-

рых относительно велика. Таким образом, для получения большого потока ин-

формации на выходе источника необходимо не только обеспечить по возмож-

ности большую энтропию на символ, но и правильно выбрать длительность

разных символов.

Контрольные вопросы

1. Дайте определение эргодическому источнику.

2. Запишите выражение для энтропии эргодического источника, когда кор-

релятивные связи имеются между двумя и тремя символами.

3. Приведите диаграмму переходов, когда источник имеет четыре харак-

терных состояния.

4. Перечислите свойства энтропии эргодических источников.

5. Что характеризует избыточность источника сообщений?

6. Что понимается под потоком информации источника сообщений?

с. 131-139; 8 с. 768-778].

3. ИСТОЧНИКИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ

3.1. Дифференциальная энтропия

Источники информации, множество возможных состояний которых со-

ставляют континуум, называют непрерывными.

Во многих случаях они преобразуются в дискретные посредством исполь-

зования устройств дискретизации и квантования. Вместе с тем существует не-

мало и таких систем, в которых информация передаётся и преобразуется непо-

средственно в форме непрерывных сигналов. Примерами могут служить систе-

мы телеизмерений с частотным разделением сигналов.

Основные информационные характеристики источников непрерывных со-

общений следующие: энтропия, условная энтропия, эпсилон

–

энтропия, эпси-

лон

–

производительность, избыточность, объём информации.

Формулу для энтропии источника непрерывных сообщений получают пу-

тем предельного перехода из формулы (1.14) для энтропии дискретного источ-

ника. С этой целью разобьём диапазон изменения непрерывной случайной ве-

личины Х, характеризующейся плотностью распределения вероятностей W(X),

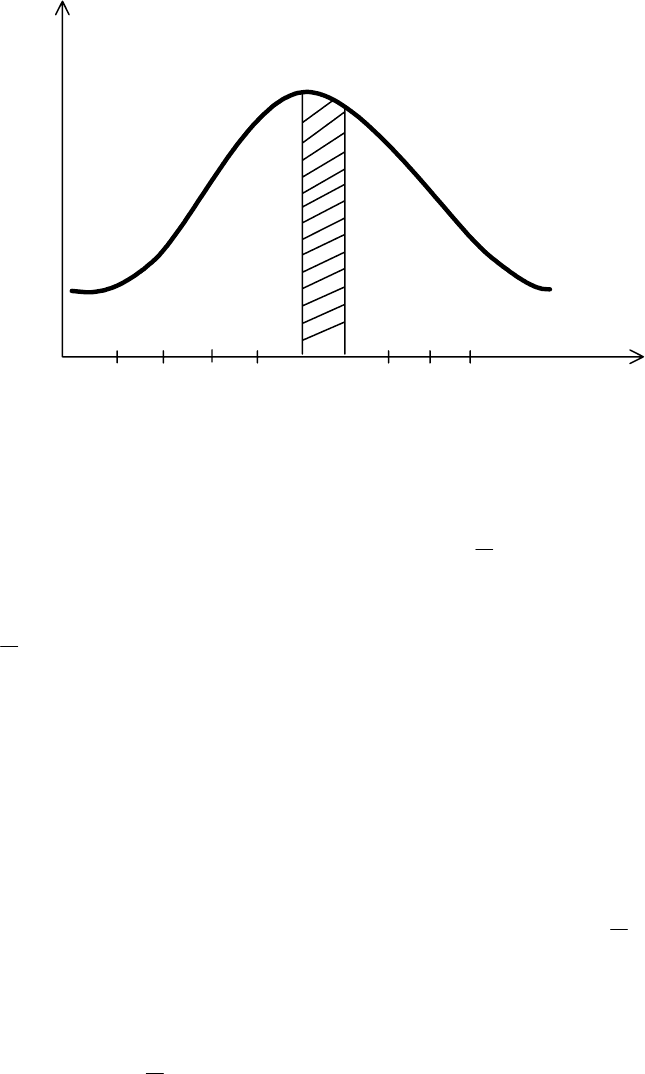
на конечное число m малых интервалов шириной ∆x (рис. 3.1).

При реализации

любого значения х, принадлежащего интервалу [x

, x

+∆x],

будем считать, что реализовалось значение x

дискретной случайной величины

Х. Поскольку ∆x мало, то вероятность

)( xxxxP

∆

≤

реализации значения

х из интервала [x

, x

+∆x] равна

.)()()( xxWdxxWxxxxP

∆≈=∆+<<

∫

∆+

12 3

∆

W(x)

Рис. 3.1. Зависимость плотности распределения вероятностей

случайной величины

Тогда энтропия дискретной случайной величины

может быть записана

в виде

,log)(log)(log)(

)(log)()(log)()(

xxWxxWxxxW

xWxxWxxWxxWXH

∆−∆−=∆∆−

−∆−=∆∆−=

∑∑

(3.1)

так как

∑

=∆

xxW

.1)(

По мере уменьшения

)( xxxxPx

∆

все больше приближается к ве-

роятности P(x

), равной нулю, а свойства дискретной величины

– к свойст-

вам непрерывной случайной величины Х.

В результате предельного перехода при 0→

∆

получено

∫

∞

−

→∆→∆

∆−−=−= .loglim)(log)()(lim)(

xdxxWxWXHXH

(3.2)

Первый член выражения (3.2) зависит только от закона распределения не-

прерывной случайной величины Х и имеет такую же структуру, как энтропия

дискретного источника. Второй член

∆

→∆

loglim

стремится к бесконечности,

это полностью соответствует интуитивному представлению о том, что неопре-

деленность выбора из бесконечно большого числа возможных состояний (зна-

чений) бесконечно велика.

Чтобы избавить теорию от бесконечности, имеется единственная возмож-

ность – ввести относительную меру неопределенности исследуемой непрерыв-

ной случайной величины Х по отношению к заданной Х

. В качестве заданной

величины Х

возьмем непрерывную случайную величину, равномерно распре-

деленную на интервале с шириной

−

. Тогда её плотность вероятности

ε1)(

=XW

, а энтропия

xxdxXH

∆loglimεlog∆loglim

log

)(

0∆

→→

−=−−=

∫

Положив для простоты записи ε = 1, составим разность

,)()log()()()(

∫

∞

−

∆

−=−= dxXWXWXHXHXH

(3.3)

которая показывает, насколько неопределенность непрерывной случайной ве-

личины Х с законом распределения W(X) больше

[

]

0)( >

∆

или меньше

неопределенности случайной величины, распределенной равномер-

но на интервале ε = 1. Поэтому величину

[

0)( <

∆

]

∫

∞

−

∆

= dxXWXWXH )(log)()( (3.4)

называют относительной дифференциальной энтропией или просто дифферен-

циальной энтропией непрерывного источника информации (непрерывного рас-

пределения случайной величины Х). В отличие от энтропии источников дис-

кретных сообщений

может принимать положительные, отрицательные

и нулевые значения. Величиной

можно характеризовать информацион-

ные свойства источников непрерывных сообщений.

)(XH

∆

)(XH

∆

Аналогично, используя операции квантования и предельного перехода,

найдем выражение для условной энтропии непрерывного источника сообще-

ний.

xdxdy

yxW

yxWYXH

∆loglim

)(

),(

log),()(

0∆ →

∞

∞−

∞

∞−

−−=

∫∫

. (3.5)

Обозначим первый член через

)( YXH

∆

dxdy

yxW

yxWYXH

)(

),(

log),()(

∆

∫∫

∞

∞−

∞

∞−

−=

. (3.6)

Эта величина конечна и называется относительной дифференциальной ус-

ловной энтропией, или просто дифференциальной условной энтропией непре-

рывного источника. Она характеризует неопределенность выбора непрерывной

случайной величины Х при условии, что известны результаты реализации зна-

чений другой статистически связанной с ней непрерывной случайной величины

Y, и по сравнению со средней неопределенностью выбора

случайной величины

, изменяющейся в диапазоне, равном единице, и имеющей равномерное рас-

пределение вероятностей.

3.2. Свойства дифференциальной энтропии

1. Величина

изменяется при изменении масштаба измерения Х.

)(

∆

Изменим масштаб случайной величины Х в k раз, оставив неизменным

масштаб равномерно распределенной в единичном интервале случайной вели-

чины Х

, принятой за эталон. Если x

= kx, то

)(

)( =

. Тогда

∫∫

+=+−=

∫∫

⎟

⎠

⎞

⎜

⎝

⎛

−=−=

′

∞

∞−

∞

∞−

∆

∞

∞−

∞

∞−

∆

.log)()(log)(log)(

)(

log

)(

)(log)()(

kXHdxxWkdxxWxW

kdx

dxxWxWXH

(3.7)

Если одновременно изменить масштаб Х

, соотносительная неопределен-

ность также изменится, так как значение эталона будет уже иным.

Из относительности дифференциальной энтропии следует, что энтропия

может принимать положительные, отрицательные и нулевые значения.

2. Дифференциальная энтропия не зависит от конкретных значений слу-

чайной величины Х и, в частности, от изменения всех её значений на постоян-

ное. Действительно, масштаб

Х при этом не меняется и справедливо равенство

.XHdxxWxW

d(xxWxWXH

∫

∞

−

=−=

∫

=+++−=+

∞

∆

∞

∞−

∆

)()(log)(

θ)θ)(logθ)(θ)(

(3.8)

3. Если единственным ограничением для случайной величины Х является

область её возможных значений [α, β], то максимальной дифференциальной эн-