Лекции по теории передачи информации

Подождите немного. Документ загружается.

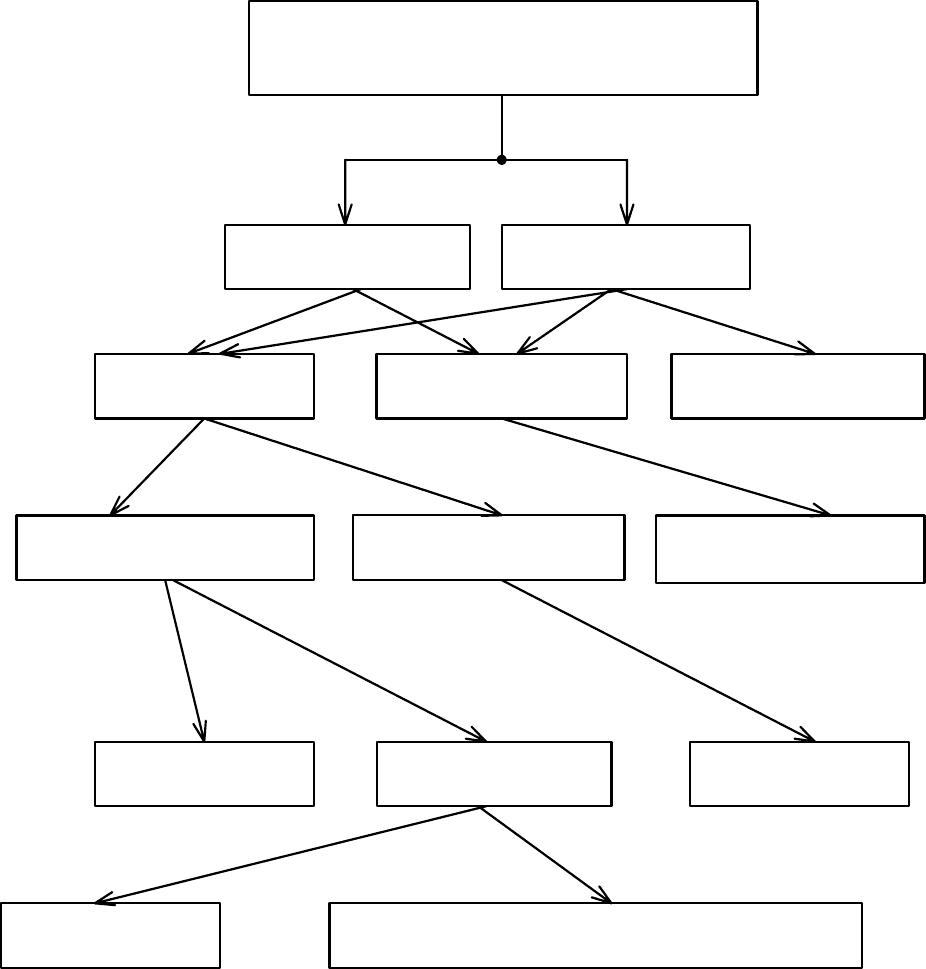
Корректирующие коды

Блочные

Непрерывные

Разделимые

Неразделимые

Рекуррентные

Систематические

Несистематические

С постоянным весом

Хемминга

Боуза-Чоудхури-Хоквингема

Циклические

Бергера

Файра

Рис. 7.1. Классификация корректирующих кодов

Среди разделимых кодов выделяют систематические и несистематические.

Систематическими кодами называют (

n, k) – коды, в которых r = n - k прове-

рочных символов являются линейными комбинациями информационных. Такое

формирование кодовых комбинаций существенно упрощает техническую реа-

лизацию устройств кодирования и декодирования – кодеков. Поэтому система-

тические коды являются одними из наиболее распространенных. Так как новую

разрешенную кодовую комбинацию можно получить линейным преобразова-

101

нием двух других разрешенных комбинаций, то такие коды часто называют ли-

нейными.

7.3. Основные характеристики корректирующих кодов

К основным характеристикам корректирующих кодов относят: избыточ-

ность кода, кодовое расстояние, число обнаруживаемых и исправляемых оши-

бок, корректирующие возможности кодов.

Принцип обнаружения и исправления ошибок кодами хорошо иллюстри-

руется с помощью геометрических моделей. Любой

n – элементный двоичный

код можно представить

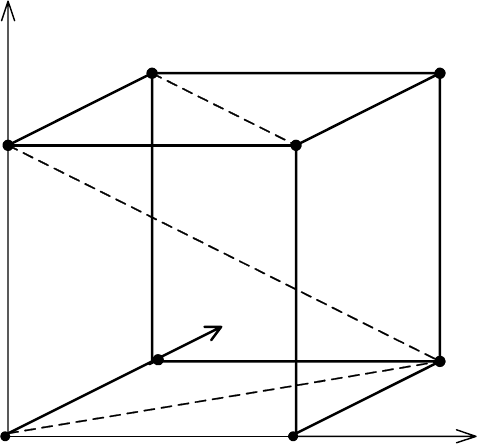
n-мерным кубом (рис.7.2), в котором каждая вершина

отображает кодовую комбинацию, а длина ребра куба соответствует одной

единице. В таком кубе расстояние между вершинами (кодовыми комбинация-

ми) измеряется минимальным количеством ребер, находящимся между ними,

обозначается

d и называется кодовым расстоянием Хемминга.

К2

К1

К3

110

011 111

100

010

000

001

101

Рис. 7.2. Геометрическая модель двоичных кодов

Таким образом, кодовое расстояние – это минимальное число элементов, в

которых любая кодовая комбинация отличается от другой (по всем парам кодо-

вых слов). Например, код состоит из комбинаций 1011, 1101, 1000 и 1100.

Сравнивая первые две комбинации, путем сложения их по модулю два нахо-

дим, что

d = 2. Сравнение первой и третьей комбинаций показывает, что и в

этом случае

d = 2. Наибольшее значение d = 3 обнаруживается при сравнении

первой и четвертой комбинаций, а наименьшее

1 – второй и четвертой,

102

третьей и четвертой комбинаций. Таким образом, для данного кода минимум

расстояния

min

= 1.

В общем случае кодовое расстояние между двумя комбинациями двоично-

го кода равно числу единиц, полученных при сложении этих комбинаций по

модулю два. Такое определение кодового расстояния удобно при большой раз-

рядности кодов. Так, складывая комбинации

1111010

0101101

1010111

⊕

определим, что кодовое расстояние между ними d = 5.

Если использовать все восемь кодовых комбинаций, записанных в верши-

нах куба, то образуется двоичный код на все сочетания. Такой код является не-

помехоустойчивым, так как любое искажение приводит к кодовой комбинации,

принадлежащей данному сомножеству, а следовательно, искажение не будет

обнаружено. Если же уменьшить число используемых комбинаций с восьми до

четырех,

то появится возможность обнаружения одиночных ошибок. Для этого

выберем только такие комбинации, которые отстоят друг от друга на расстоя-

нии

d = 2, например, 000, 110, 011, 101. Остальные кодовые комбинации не ис-

пользуются. Если передавалась комбинация 101, а принята комбинация 100, то

очевидно, что при приеме произошла ошибка. Таким образом, для обнаружения

искажений необходимо все кодовые комбинации разделить на две группы: раз-

решенные и запрещенные.

Из приведенного примера можно сделать вывод, что способность кода об-

наруживать и исправлять

ошибки обусловлена наличием избыточности, кото-

рая обеспечивает минимальное расстояние между любыми двумя разрешенны-

ми комбинациями

, т.е. к исходной k – элементной комбинации необ-

ходимо добавить

r контрольных символов, сформированных по определенным

правилам.

min

>=d

Пусть на вход кодирующего устройства поступает последовательность из

информационных двоичных символов. На выходе ей соответствует последова-

тельность из

n = k + r двоичных символов.

Всего может быть

разрешенных кодовых комбинаций и различных

выходных последовательностей, а следовательно,

−

возможных выход-

ных последовательностей для передачи не используются и являются запрещен-

ными комбинациями.

Искажение информации в процессе передачи сводится к тому, что некото-

рые из переданных символов заменяются другими. Так как каждая из 2

раз-

решенных комбинаций в результате действия помех может трансформировать-

ся в любую другую, то всего имеется 2

×2

возможных случаев передачи

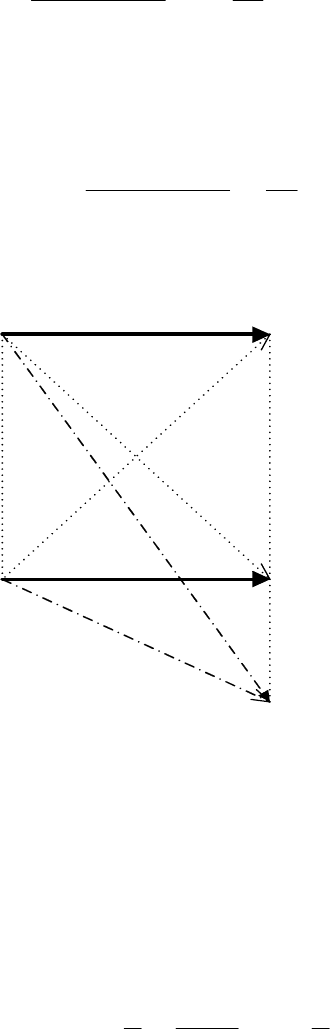
(рис. 7.3). В это число входят: 2

случаев безошибочной передачи (на рис. 7.3

обозначены жирными линиями):

103

)12(2 −

случаев перехода в другие разрешенные комбинации, что соот-

ветствует необнаруженным ошибкам (на рис. 7.3 обозначены пунктирными ли-

ниями);

)22(2

knk

− случаев перехода в запрещенные комбинации, которые могут

быть обнаружены (на рис. 7.3 обозначены штрихпунктирными линиями). Сле-

довательно, число обнаруживаемых ошибочных кодовых комбинаций от обще-

го числа возможных случаев передачи составляет:

222

)(

knk

−=

−

. (7.1)

Отношение числа исправляемых кодом ошибочных кодовых комбинаций к

числу обнаруживаемых ошибочных комбинаций равно:

)

(

kknk

−

. (7.2)

Рис. 7.3. Возможные варианты трансформаций

кодовых комбинаций

в B

Из приведенных выше рассуждений можно сделать вывод, что коррекция

ошибок возможна благодаря введению избыточности, которая определяется

выражением:

−=

−

== 1

. (7.3)

104

Эта величина показывает, какую часть от общего числа символов кодовой

комбинации составляют контрольные символы. В теории кодирования величи-

ну

k/n принято называть скоростью передачи [5]. Необходимо отметить, что ве-

личина

k/n характеризует относительную скорость передачи информации. Если

производительность источника информации равна

)(xH

бит/с, то скорость пере-

дачи после кодирования этой информации окажется равной

kxH

)(

. (7.4)

Для обнаружения или исправления значительного числа ошибок, необхо-

димо иметь код с большим числом проверочных символов. При этом сущест-

венно возрастает длительность кодовых блоков, что приводит к задержке ин-

формации при передаче и приеме.

Если длительность помехи превосходит длительность элементарного сиг-

нала, то искажается несколько символов, и такой вид

искажений называется па-

кетом (пачкой) искажений. Под пакетом искажений длиной

b понимается такой

вид комбинации помехи, в которой между крайними разрядами, пораженными

помехами, содержатся

b – 2 разряда. Например, при b = 4 пакет искажений мо-

жет иметь вид: 1001 (поражены только два крайних символа), 1111 (поражены

все символы), 1011 (не поражен лишь один символ). При любом варианте не-

пременным условием пакета данной длины является поражение крайних сим-

волов.

Кодовое расстояние, как отмечалось выше, является основной характе-

ристикой корректирующей способности данного кода. Если код используется

только

для обнаружения ошибок кратности m, то необходимо и достаточно,

чтобы минимальное расстояние удовлетворяло условию

min

≥ m

. (7.5)

Под кратностью ошибки понимают число позиций кодовой комбинации, в

которых под действием помехи одни символы оказались замененными други-

ми.

Для исправления ошибки кратностью

S необходимо, чтобы минимальное

расстояние удовлетворяло условию

min

≥

. (7.6.)

Корректирующие коды можно одновременно использовать и для обнару-

жения и для исправления ошибок. В этом случае кодовое расстояние должно

удовлетворять условию

105

min

(7.7)

где всегда должно выполняться условие

m > S.

Вопрос о минимально необходимой избыточности, при которой код обла-

дает нужными корректирующими свойствами, является одним из важнейших в

теории кодирования. Для некоторых частных случаев Хемминг указал простые

соотношения, позволяющие определить необходимое число проверочных сим-

волов:

)1log(

≥∈

, (7.8)

))1log()1log((

∈

≥∈

kkr

, (7.9)

2log

≥∈

, (7.10)

где знак

∈ означает округление в большую сторону.

7.4. Способы введения избыточности в сигнал

Для корректирования ошибок можно применять те же способы, что и для

повышения скорости передачи информации. Все они направлены на увеличе-

ние объема сигнала и приближение его к объему канала. Если объем сигнала

равен объему канала, то корректирования ошибок можно добиться только пу-

тем уменьшения скорости передачи информации, так как часть

сигналов может

быть использована для корректирования. Корректирующее кодирование ис-

пользует по существу все виды избыточности сигналов: временную, частотную

и энергетическую. Если длина кодовой комбинации не фиксирована (скорость

передачи информации не фиксирована), то для корректирования ошибок ис-

пользуют временную избыточность – кроме информационных символов, до-

полнительно вводят еще проверочные.

Если скорость передачи информации

фиксирована, ввести проверочные

символы в кодовую комбинацию бинарного кода можно, лишь уменьшая дли-

тельность элементарных сигналов, что ведет к расширению их спектра. Следо-

вательно, в этом случае корректирующее кодирование использует частотную

избыточность. Чтобы отношение сигнал/шум с уменьшением длительности им-

пульсов не падало, необходимо увеличить амплитуду импульсов. Увеличивая

амплитуду укороченного

импульса, можно настолько увеличить его энергию,

что вероятность ошибки при его приеме уменьшится по сравнению с вероятно-

стью при приеме импульса неукороченной длительности. Так вводится энерге-

тическая избыточность.

106

7.5. Систематические коды

Систематическими кодами называются блочные (

n, k) коды, у которых k

(обычно первые) разряды представляют собой двоичный неизбыточный код, а

последующие

r-контрольные разряды сформированы путем линейных комби-

наций над информационными.

Основное свойство систематических кодов: сумма по модулю два двух и

более разрешенных кодовых комбинаций также дает разрешенную кодовую

комбинацию.

Правило формирования кода обычно выбирают так, чтобы при декодиро-

вании имелась возможность выполнить ряд проверок на четность для некото-

рых определенным образом выбранных

подмножеств информационных и кон-

трольных символов каждой кодовой комбинации. Анализируя результаты про-

верок, можно обнаружить или исправить ошибку ожидаемого вида.

Информацию о способе построения такого кода содержит проверочная

матрица, которая составляется на базе образующей матрицы.

Образующая матрица

М состоит из единичной матрицы размерностью k×k

и приписанной к ней справа матрицы дополнений размерностью

k×r:

1000

0100

0010

0001

33231

22221

11211

krkk

bbb

LLLL

LLLLL

(7.11)

Размерность матрицы дополнений выбирается из выражения (7.8) или

(7.9). Причем вес w (число ненулевых элементов) каждой строки матрицы до-

полнений должен быть не меньше, чем d

min

– 1.

Проверочная матрица N строится из образующей матрицы следующим об-

разом. Строками проверочной матрицы являются столбцы матрицы дополнений

образующей матрицы. К полученной матрице дописывается справа единичная

матрица размерностью r×r. Таким образом, проверочная матрица размерностью

r×k имеет вид:

1000

0010

0001

321

2322212

1312111

LLLLLLLLLL

krrrr

bbbb

N = (7.12)

107

Единицы, стоящие в каждой строке, однозначно определяют, какие симво-

лы должны участвовать в определении значения контрольного разряда. Причем

единицы в единичной матрице определяют номера контрольных разрядов.

Пример 7.1. Получить алгоритм кодирования в систематическом коде всех

четырехразрядных кодовых комбинаций, позволяющий исправлять единичную

ошибку. Таким образом, задано число информационных символов k = 4 и крат-

ность исправлений S = 1. По выражению (7.9) определим число контрольных

символов:

3))14log()14log((

∈

≥∈

Минимальное кодовое расстояние определим из выражения (7.6):

.3112

min

⋅

≥d

Строим образующую матрицу:

1111000

1010100

0110010

1100001

Проверочная матрица будет иметь вид

1001101

0101011

0011110

7654321

aaaaaaa

Обозначим символы, стоящие в каждой строке, через

Символы

и примем за контрольные, так как они будут входить только

в одну из проверок.

).(

7654321

aaaaaaaa

, aa

Составим проверки для каждого контрольного символа. Из первой строки

имеем

4325

aaaa

⊕

(7.13)

Из второй строки получим алгоритм для формирования контрольного сим-

вола a

4216

aaaa

⊕

(7.14)

108

Аналогично из третьей строки получим алгоритм для формирования контроль-

ного символа

4317

aaaa

⊕

(7.15)

Нетрудно убедиться, что все результаты проверок на четность по выраже-

ниям (7.13)–(7.15) дают нуль, что свидетельствует о правильноcти составления

образующей и проверочной матриц.

Пример 7.2. На основании алгоритма, полученного в примере 7.3, закоди-

ровать кодовую комбинацию

4321

1101)( aaaaxG

в систематическом коде,

позволяющим исправлять одиночную ошибку. По выражениям (7.13), (7.14) и

(7.15) найдем значения для контрольных символов

и :

, aa

,0101

⊕

,1111

⊕

.0101

⊕

(7.16)

Таким образом, кодовая комбинация F(X) (7.16) в систематическом коде

будет иметь вид

F(X) = 1 1 0 1 0 1 0 . (7.17)

На приемной стороне производятся проверки Si принятой кодовой комби-

нации, которые составляются на основании выражений (7.13), (7.14) и (7.15):

74313

64212

54321

aaaaS

⊕⊕⊕=

⊕

(7.18)

Если синдром (результат проверок на четность) S

будет нулевого по-

рядка, то искажений в принятой кодовой комбинации F’(X) нет. При наличии

искажений синдром S

указывает на искаженный символ.

109

Рассмотрим всевозможные состояния S

0 0 0 – искажений нет,

1 0 0 – искажен символ а

0 1 0 – искажен символ а

0 0 1 – искажен символ а

1 1 0 – искажен символ а

0 1 1 – искажен символ а

1 1 1 – искажен символ а

1 0 1 – искажен символ а

. (7.19)

Пример 7.3. Кодовая комбинация F(X) = 1 1 0 1 0 1 0 (пример 7.2) при пе-

редаче была искажена и приняла вид F′(X) = 1 1 1 1 0 1 0 = а

Декодировать принятую кодовую комбинацию.

Произведем проверки согласно выражениям (7.18):

10111

⊕

01111

⊕

10111

⊕

Полученный синдром S

= 101 согласно (7.19) свидетельствует об ис-

кажении символа а

. Заменяем этот символ на противоположный и получаем

исправленную кодовую комбинацию F(X) = 1

0, а исходная кодовая

комбинация имеет G(X) = 1

1, что совпадает с кодовой комбинацией, подле-

жащей кодированию в примере 7.2.

7.6. Рекуррентные коды

Эти коды относятся к непрерывным кодам, в которых операции кодирова-

ния и декодирования производятся непрерывно над последовательностью ин-

формационных символов без деления на блоки. Рекуррентные коды применя-

ются для обнаружения и исправления пакетов ошибок. В данном коде после

каждого информационного элемента следует проверочный элемент. Провероч-

ные элементы формируются путем сложения по

модулю два двух информаци-

онных элементов, отстоящих друг от друга на шаг сложения, равный b.

Рассмотрим процесс кодирования на примере кодовой комбинации, приве-

денный на рис. 7.4 (верхняя строка), если шаг сложения b = 2. Процесс образо-

вания контрольных символов показан на этом же рисунке (нижняя строка).

110