Лекции по теории передачи информации

Подождите немного. Документ загружается.

Значение Р

находится в пределах

,10

следовательно,

logPI

−

всегда положительная величина.

Количество информации

log

−

, где Р – вероятность события, было

положено в основу и было исходной точкой создания теории информации.

1.2. Энтропия ансамбля

Ансамблем называется полная совокупность состояний с вероятностями их

появлений, составляющими в сумме единицу:

⎟

⎠

⎞

⎜

⎝

⎛

PPPP

XXXX

(1.9)

причем

∑

Пусть имеет место N возможных исходов опыта, из них k разных, и i-й ис-

ход (i = 1, 2,..., k) повторяется n

раз и вносит информацию, количество которой

оценивается как I

. Тогда средняя информация, доставляемая одним опытом,

равна

2211

InInIn

ÑÐ

(1.10)

Но количество информации в каждом исходе согласно (1.8) будет

.log

−

(1.11)

Тогда

)log()log()log(

2211

PnPnPn

ÑÐ

−

(1.12)

Но отношение

представляют собой частоты повторения исходов, а

следовательно, могут быть заменены их вероятностями:

. (1.13)

Подставляя (1.13) в (1.12), получим

.log)log()log()log(

2211

∑

−=−++−+−=

iikkÑÐ

PPPPPPPPI L

Полученную величину К.

Шеннон назвал энтропией и обозначил буквой Н,

бит:

∑

−==

log

. (1.14)

Энтропия Н представляет собой логарифмическую меру беспорядочности

состояния источника сообщений и характеризует степень неопределенности со-

стояния этого источника. Получение информации – это процесс раскрытия не-

определенности.

В информационных системах неопределенность снижается за счёт приня-

той информации, поэтому численно энтропия Н равна среднему количеству

информации, несомой произвольным исходом x

, т.е. является количественной

мерой информации.

Если все k различных состояний источника равновероятны, то

энтропия максимальна и из (1.14) имеем

log

max

∑

−=

. (1.15)

Нетрудно заметить, что в частном случае при равновероятных сообщениях

формулы (1.14) и (1.5) совпадают. Совпадение оценок количества информации

по Шеннону и Хартли свидетельствуют о полном использовании информаци-

онной емкости системы. В случае неравных вероятностей количество информа-

ции по Шеннону меньше информационной емкости системы.

1.3. Энтропия объединения

Объединением называется совокупность двух и более взаимозависимых

ансамблей дискретных случайных переменных.

Рассмотрим объединение, состоящее из двух ансамблей X и Y, например из

двух дискретных измеряемых величин, связанных между собой вероятностны-

ми зависимостями. Объединение ансамблей характеризуется матрицей P(X,Y)

вероятностей P(x

, y

) всех возможных комбинаций состояний

)1( nix

≤

ан-

самбля X и состояний

ансамбля Y:

)1( miy

≤≤

),(),(),(

),(

1111

mnmim

jnjij

yxPyxPyxP

YXP

LLLLL

. (1.16)

Cуммируя столбцы и строки матрицы (1.16), получим информацию об ан-

самблях X и Y исходных источников:

)()()(

yPyPyP

yyy

xPxPxP

xxx

(1.17)

где

),()(

yxPxP

∑

),()(

yxPyP

∑

Вероятности P(x

) совместной реализации взаимозависимых состояний x

и y

можно выразить через условные вероятности P(x

) или P(y

) в соответ-

ствии с тем, какие состояния принять за причину, а какие – за следствие.

),/()()/()(),(

jijijiji

yxPyPxyPxPyxP

(1.18)

где

– вероятность реализации состояний x

)/(

yxP

ансамбля X при условии,

что реализовалось состояние y

ансамбля Y; – вероятность реализации

состояний y

)/(

xyP

ансамбля Y при условии, что реализовалось состояние x

ансамбля

Тогда выражение для энтропии объединения в соответствии с (1.14) при-

нимает вид:

∑∑∑

∑∑

===

−−=

=−=

ijiii

iji

xyPxyPxPxPxP

xyPxPxyPxP

yxPyxPYXH

111

,)/(log)/()()(log)(

)/()(log)/()(

),(log),(),(

(1.19)

где ) – случайная величина, характеризующая неоп-

ределенность, приходящуюся на одно состояние ансамбля Y при условии, что

реализовалось конкретное состояние x

/(log)/(

xyPxyP

∑

−

ансамбля X . Назовем её частной услов-

ной энтропией ансамбля Y и обозначим H(Y/x

)./(log)/()/(

iji

xyPxyPxYH

∑

−= (1.20)

При усреднении по всем состояниям ансамбля X получаем среднюю неоп-

ределенность, приходящуюся на одно состояние ансамбля Y при известных со-

стояниях ансамбля X:

∑∑

∑

−=

=−=

ijij

xyPxyPxPxP

xYHxPXYH

)./(log)/()()(

)/()()/(

(1.21)

Величину H(Y/X) называют полной условной или просто условной энтро-

пией ансамбля Y по отношению к ансамблю X.

Подставляя (1.21) в (1.19), получаем

()(),( X

(1.22)

Выражая

через другую условную вероятность в соответствии с

(1.18), найдем

),(

yxP

()(),(

(1.23)

где

)/()()/(

yXHyPYXH

∑

= (1.24)

(1.25)

)./(log)/()/(

jij

yxPyxPyXH

∑

−=

Таким образом, энтропия объединения двух статистически связанных ан-

самблей X и Y равна безусловной энтропии одного ансамбля плюс условная эн-

тропия другого относительно первого.

В случае статистической независимости ансамблей X и Y имеют

).()(),(

jiji

yPxPyxP

Тогда

∑∑∑∑

∑∑

====

−−=

=−=

jii

xPyPyPyPxPxP

yPxPyPxPYXH

1111

.)()(log)()()(log)(

)()(log)()(),(

Учитывая, что

1)(

∑

yP и ,

1)(

∑

получим

).,()()(),( X

(1.26)

1.4. Свойства энтропии

1.4.1. Энтропия всегда неотрицательна, так как значения вероятностей вы-

ражаются дробными величинами, а их логарифмы – отрицательными величи-

нами (1.14).

1.4.2.

Энтропия равна нулю в том крайнем случае, когда одно событие

равно единице, а все остальные – нулю. Это положение соответствует случаю,

когда состояние источника полностью определено.

1.4.3. Энтропия имеет наибольшее значение при условии, когда все веро-

ятности равны между собой (1.15).

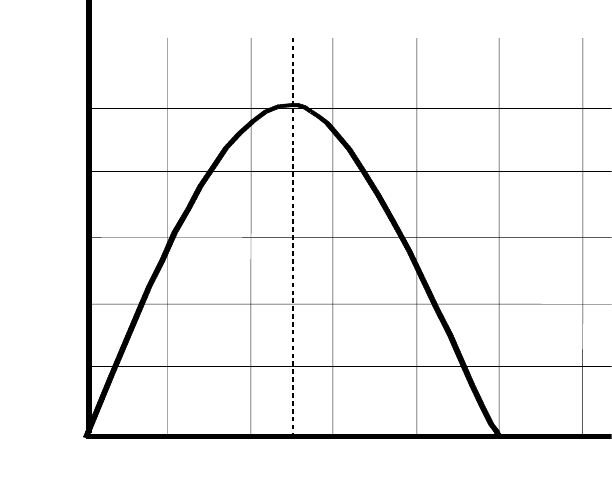
1.4.4. Энтропия источника Х с двумя состояниями х

и х

изменяется от ну-

ля до единицы, достигая максимума при равенстве их вероятностей

Р(х

) = Р = Р(х

) = 1 - Р = 0,5.

График зависимости Н(Х) в функции Р:

Н(Х) =-[PlogP + (1-P)log(1-P)], (1.27)

приведен на рис. 1.1.

Отметим, что энтропия непрерывно зависит от вероятности отдельных со-

стояний, что непосредственно вытекает из непрерывности функции -PlogP.

1.4.5. Энтропия объединения нескольких статистически независимых ис-

точников информации равна сумме энтропий

исходных источников

H(X,Y,Z,..., W) = H(X) + H(Y) + H(Z) + ... + H(W). (1.28)

1.4.6. Энтропия объединения двух статистически связанных ансамблей X и

Y равна

).,()(),( X

1.4.7. Энтропия объединения любого числа зависимых ансамблей опреде-

ляется из выражения

...).,,

(...),

()

()(),...,,,(

(1.29)

0,2

0,4

0,6

0,8

0,2

0,4

0,6

0,8

1,0

0,5

, дв.ед.

Рис. 1.1. Зависимость Н(Х) в функции Р

1.4.8. Энтропия не зависит от значений, принимаемых случайными вели-

чинами, а зависит только от вероятностей их появления (1.14).

1.4.9. Если события x

и y

статистически независимы при любых i и j, то

H(Y/X) = H(Y) и H(X/Y) = H(X). (1.30)

Таким образом, сведения о результатах выбора состояний из одного ан-

самбля не снижает неопределенности выбора состояний из другого ансамбля.

Если имеет место однозначная связь в реализациях состояний

)1( nix

≤

из

ансамбля X и

)1( njy

≤

из ансамбля Y, то условная энтропия любого из ан-

самблей равна нулю:

H(Y/X) = 0, H(X/Y) = 0. (1.31)

Действительно, условные вероятности P(x

) и P(y

) в этом случае при-

нимают значения, равные нулю или единице. Поэтому все слагаемые, входящие

в выражения (1.20) и (1.25), для частных условных энтропий равны нулю. Тогда

в соответствии с (1.21) и (1.24) условные энтропии равны нулю.

Равенства (1.31) отражают факт отсутствия дополнительной неопределен-

ности при выборе событий из второго ансамбля.

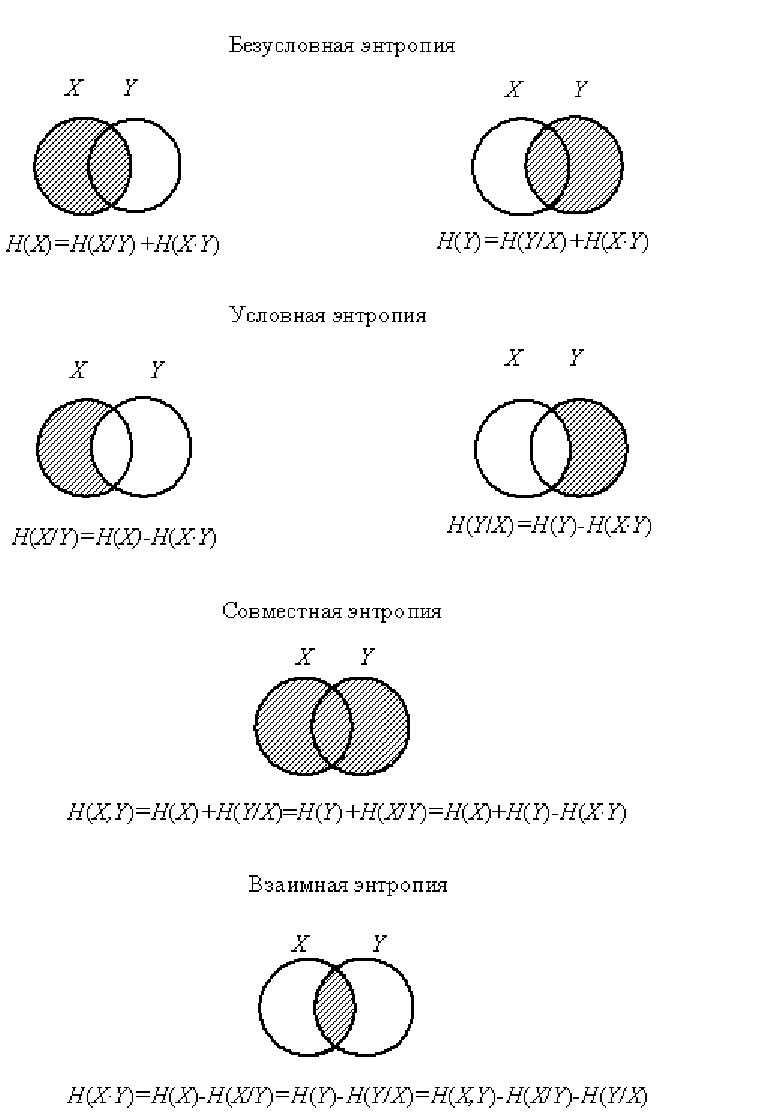
Уяснению соотношений между рассмотренными энтропиями дискретных ис-

точников информации (ансамблей) соответствует их графическое отображение

(рис. 1.2).

Рис. 1.2. Энтропия объединения

1.5. Количество информации от опыта в общем случае

Передача информации инициируется либо самим источником информации,

либо осуществляется по запросу. На приемной стороне любой системы переда-

чи информации до получения сигнала от интересующего нас источника неиз-

вестно, какой из возможных сигналов будет передан, но считается известным

распределение вероятностей Р(x

) по всем сигналам. Неопределенность ситуа-

ции до приема сигнала характеризуется энтропией:

).(log)()(

xPxPXH

∑

−=

(1.32)

Далее в приемное устройство поступает принятый сигнал. Поскольку

предполагается, что принятый сигнал соответствует переданному (помехи от-

сутствуют), то неопределенность относительно источника информации снима-

ется полностью.

Таким образом, в результате приема сигнала, с одной стороны, произошло

уменьшение неопределенности с Н(Х) до нуля, а с другой стороны, получено

количество информации I, численно

равное энтропии Н(Х). Отсюда следует,

что количество информации может быть определено как мера снятой неопреде-

ленности. Численное значение количества информации о некотором объекте

равно разности энтропий объекта до и после приема сигнала. Значит, понятие

энтропия является первичным, исходным, а понятие количество информации –

вторичным, производным понятием. Энтропия есть мера неопределенности,

количество информации – мера изменения неопределенности.

Если помехи существуют, то принятый сигнал в той или иной степени не

тождественен переданному. Здесь исчезает численное совпадение I и H. Коли-

чество информации будет меньше, чем при отсутствии помех, так как прием

сигнала не уменьшает энтропию до нуля.

Рассмотрим случай, когда между элементами сообщения

и помехой стати-

стические связи отсутствуют, искажения отдельных элементов сообщения яв-

ляются событиями независимыми и адресату известна совокупность условных

вероятностей

)1,1()/( mjmiyxP

≤

≤≤

того, что вместо элемента сооб-

щения x

будет принят элемент сообщения y

Среднее количество неопределенности, которым мы обладали до опыта,

равнялось Н(Х). Представим теперь что мы приняли какой-то сигнал y

и оцени-

ваем, какова неопределенность (после опыта) соответствия его некоторому пе-

реданному x

. Эта неопределенность равна

H(x

) = -logP(x

). (1.33)

Как видим, неопределенность этого соответствия является случайной ве-

личиной, значения которой при каждом заданном y

наступают с вероятностями

P(x

). Поэтому среднее значение количества неопределенности соответствия

данного y

любому из x

равно

)./(log)/()/(

jij

yxPyxPyXH

∑

−=

(1.34)

Величина H(X/y

) также случайна. Вероятности её значений равны P(y

Тогда среднее значение H(X/y

) определит среднее количество неопределённо-

сти соответствия любого y

любому из x

. Обозначим это среднее H(X/Y):

(1.35)

)./(log),()()/()/(

111

jij

yxPyxPyPyXHYXH

∑∑∑

===

−==

Другими словами, H(X/Y) есть средняя неопределённость в передаче того

или иного x

, если известно, что принят тот или иной y

, или, кратко, средняя

неопределённость ансамбля X после опыта.

Таким образом, мы установили, что неопределённость передачи некоторо-

го сигнала Х до опыта Н(Х), а после опыта H(X/Y). Поэтому количество инфор-

мации, имеющееся в Y o X:

I(Y,X) = H(X) – H(X/Y). (1.36)

Эта мера количества информации получена нами на примере передачи со-

общений по каналу связи. Совершенно аналогичные рассуждения могут быть

применены к случайным объектам произвольного вида и приведут нас к той же

мере.

Подставим в выражение (1.36) необходимые значения H(X) и H(X/Y) из

(1.32) и (1.35) соответственно получим

∑∑

∑∑ ∑∑

∑∑∑

== ==

===

=+=

=+−=

ijiiji

jijiii

yPxP

yxP

yxPyxPxPyxP

yxPyxPxxPXYI

11 11

111

)()(

),(

log),(

)/(log),()(log),(

)/(log),()log()(),(

(1.37)

Если частный характер количества информации специально не оговарива-

ется, мы всегда имеем дело с количеством информации, приходящимся в сред-

нем на один элемент сообщения. Поэтому указание об усреднении опускаются.

1.6. Основные свойства количества информации

1.6.1. I(X,Y) = I(Y,X), т.е. количество информации, содержащееся в случай-

ном объекте Y о случайном объекте Х, равно количеству информации, содер-

жащемуся в случайном объекте Х о случайном объекте Y. Свойство 1.6.1 сразу

же следует из (1.37), если учесть, что P(x

) = P(y

) .

1.6.2. ,0),( ≥

причём знак равенства имеет место, когда объекты X и Y

независимы.

Положительность I(X,Y) следует из свойства энтропии : если события x

и y

статистически зависимы, то всегда H(Y/X) < H(Y) и H(X/Y) < H(X).

1.6.3. I(X,Y) = H(X), т.е. энтропия может быть истолкована как информация,

содержащаяся в объектах относительно самих себя. Из этого также непосредст-

венно вытекает, что энтропия есть максимальное количество информации, ко-

торое можно получить

об объекте. Это возможно при взаимно однозначном со-

ответствии между множествами передаваемых и принимаемых сообщений, что

имеет место в отсутствии помехи, апостериорная энтропия равна нулю и коли-

чество информации численно совпадает с энтропией источника.

Контрольные вопросы

1. В чём сущность требования аддитивности к мере неопределённости вы-

бора?

2. Назовите основной недостаток меры неопределённости, предложенной

Р. Хартли.

3. Укажите достоинства и недостатки способа, предложенного

К. Шенноном.

4. Что необходимо учитывать при выборе способа измерения количества

информации?

5. В каких единицах измеряется количество информации?

6. Дайте определение энтропии.

7. Назовите основные свойства

энтропии дискретного ансамбля.

8. Почему вводится понятие условной энтропии? Запишите выражение для

условной энтропии и поясните её смысл.

9. Приведите выражение для энтропии двух взаимосвязанных ансамблей.

10. Как связаны между собой понятия количества информации и энтропии?

11. В чём различаются понятия частного и среднего количества информа-

ции?

12. Когда энтропия источника с двумя

состояниями достигает максимума?

13. От чего не зависит энтропия случайного процесса?

14. Запишите выражение для энтропии объединения нескольких независи-

мых источников информации.

15. Перечислите свойства количества информации.

[1 с. 97-110; 2 с. 35-44; 6 с. 23-25].