Лекции - Электромагнитные поля и волны
Подождите немного. Документ загружается.


31
таком режиме – запредельной. Режим отсечки важен для понимания процессов при наруше-
нии регулярности линии передачи. В результате таких нарушений возникают волны высших
типов, для которых условие распространения не выполняется. Из формул (61) видно, что ха-
рактеристическое сопротивление при этом становится мнимой величиной, так что линия пе-
редачи действует на генератор как реактивное сопротивление, отражающее всю энергию об-
ратно к источнику. Следовательно, затухание волн в режиме отсечки вызвано не поглощени-
ем энергии в линии, а её отражением.
10. Направляемые волны в прямоугольном металлическом волноводе
В прямоугольном волноводе, являющемся частным случаем линии передачи, в кото-
рой энергия распространяется внутри полой металлической трубы, могут существовать вол-
ны Е и Н и невозможно существование волн типа Т. Исследование волн в прямоугольном
волноводе обычно проводится при следующих предпосыл-
ках: стенки волновода являются идеально проводящим
(σ=∞ ); волновод заполнен вакуумом (воздухом). Эти до-
пущения существенно упрощают анализ поля, не нарушая
общности задачи, так как реальные волноводы выполня-
ются из металлов с высокой удельной электропроводно-
стью, а воздух, заполняющий волновод, по своим электрическим параметрам идентичен ва-
кууму. Полый металлический волновод прямоугольного сечения изображен в декартовой
системе координат на рис.8.
Структура поля Е-волн, как отмечалось ранее, находится из решения уравнений (47) и
(50) с наложением следующих граничных условий 0,0 ==
n
HE
τ
. Выражения для всех ком-
понент векторов поля Е-волн имеют вид:
,)sin()cos(
,)cos()sin(
,)cos()sin(
,)sin()cos(
,)sin()sin(
)(
0
2
)(
0
2
)(
0
2
)(
0
2
)(
0
zi
a
ym
zi
a
xm
zi
ym
zi
xm
zi
zm
e
b
ym
a
xm
E
a
mi
H
e
b
ym
a
xm
E
b
ni
H
e
b
ym
a
xm
E
b
in
E
e
b
ym
a
xm
E
a
im
E
e
b
ym
a
xm
EE
β
β
β
β
β
ππ
γ
πωε
ππ
γ
πωε
ππ
γ
πβ
ππ
γ
πβ
π
π
−
⊥
=
•
−
⊥
=
•
−
⊥
•
−
⊥
•
−
=
•
−
−
=
−
=
(64)
где
Е
0
– амплитуда продольной составляющей электрического поля на продольной оси вол-
новода; m=1,2,3…; n=1,2,3…; γ
⊥
=
22
+
b
n
a
m
ππ
.
b
а
x
y
z
b<a
Рис. 8

32
Критическая длина волны определяется выражением:
λ
КР
=
22
2
+
b
n
a
m
. (65)
Из записанных выражений следует, что структура поля в плоскости поперечного сече-
ния волновода соответствует стоячим волнам, причем
m
определяет число стоячих полуволн,
укладывающихся вдоль стенки длиной а (широкой стенки),
n
– число полуволн, укладываю-
щихся вдоль стенки длиной b (узкой стенки). Ни один из этих индексов не должен равняться
нулю, так как в противном случае обращаются в ноль все компоненты векторов поля. В зави-
симости от значений чисел m и n изменяются
γ
⊥
,
f
кр
и, следовательно, все параметры волны.
Поэтому числа
m
и
n
однозначно определяют тип волны, который обозначается
Е
mn
.
Структура поля
Н
-
волн
находится аналогично
Е
-волнам. Выражения для всех компо-
нент векторов поля Н-волн имеют вид:
,)cos()sin(
,)sin()cos(
,)sin()cos(
,)cos()sin(
,)cos()cos(
)(
0
)(
0
)(
0
)(
0
)(
0
2
2
2
2
zi
a
ym
zi
a
xm
zi
ym
zi
xm
zi
zm
e
b
ym
a
xm
H
a
mi
E
e
b
ym
a
xm
H
b
ni
E
e
b
ym
a
xm
H
b
in
H
e
b
ym
a
xm
H
a
im
H
e
b
ym
a
xm
HH
β
β
β
β
β
π
π
γ
πωµ
π
π
γ
πωµ
π
π
γ
πβ
π
π
γ
πβ
π
π
−
=
•
−
=
•
−
•
−
•
−
=
•
⊥
⊥
⊥
⊥
−
−
=
=
(66)
Смысл индексов
m
и
n
такой же, что и в случае Е-волн. Один из индексов волны
Н
mn
может быть нулевым, так как при
m
=0 или
n
=0 не происходит обращения в ноль всех ком-
понент поля.
Критическая длина волны
Н
mn
определяется по формуле (65). При индексах m и n, от-
личных от нуля, значения
γ
⊥
,
f
кр
для волн
mn
E
и
mn
H
с равными индексами оказываются
одинаковыми. Следовательно, все указанные параметры у этих волн также одинаковы. В ре-
зультате условия распространения волн
mn
E
и
mn
H
с равными индексами оказываются
идентичными. Такие волны называют вырожденными.
Основная
волна
прямоугольного
волновода
. В волноводе может распространяться
большое число типов волн, отличающихся структурой поля, критической длиной волны и
другими параметрами. Однако одновременное распространение нескольких типов волн
(многоволновый, или многомодовый режим) в волноводе отрицательно сказывается на его
технико-эксплутационных показателях. Это объясняется главным образом тем, что при пе-
редаче сигнала по волноводу с помощью нескольких типов волн, скорость распространения
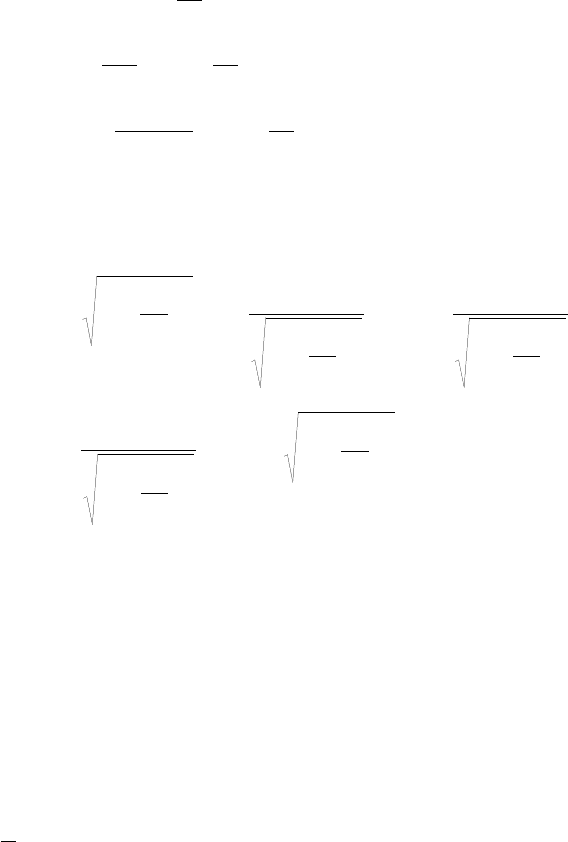
33
и фазовая скорость которых различны, в точку приема приходят сигналы с разными фазовы-
ми набегами, вследствие различного временного запаздывания отдельных типов волн. В ре-
зультате интерференции этих сигналов возникают искажения в точке приема, и повышается
уровень шумов. Характер и степень искажений зависят от способа модуляции, частотного
спектра сигнала, вида передаваемой информации и других факторов. Кроме того, поскольку
структура поля разных волн различна, в многоволновом режиме невозможно получить же-
лаемый вид поляризации. В силу этих причин к волноводу обычно предъявляется требование
обеспечения одноволнового режима работы. Проще всего такой режим работы можно полу-
чить, если использовать волну, обладающую наибольшей критической длиной волны (ос-
новную волну). Так как a>b, то, основной волной прямоугольного волновода является волна
Н
10
, для которой
кр
λ
=2а. Подставляя в (66) m=1 и n=0, получаем соотношения для состав-
ляющих поля волны Н
10
.
0
,)sin(
,)sin(
,)cos(
)(
0
)(
0
)(
0
===
−=
=
=
•••
−
⋅
•
−
•
−
•
mzmxmy
zi
а
ym
zi
xm
zi
zm
EEH
e
a
x
H
ai
E
e
a
x
H
ai
H
e
a
x
HH
β
β
β
π
π
ωµ
π
π
β
π
(67)
Основные параметры волны Н
10
определяются по формулам
β
=
2
2
1
−
a
k
λ
,
Λ
=
2
2
1
−
a
λ
λ
,
10
Н
c
Z =
2
2
1
−
a
Z
c
λ
,
V
ф
=
2
0
2
1
−
a
v
λ
, V
Э
=
2
0
2
1
−
a
v
λ
. (68)
Структура
поля
волны
Н
10
,
соответствующая
изображена
различным
сечениям
на
рис
.9.
При
построении
структуры
поля
учтены
следующие
обстоятельства
.
Так
как
волна
Н
10
не
имеет
продольной
составляющей
электрического
поля
,
то
электрические
силовые
линии
лежат
в
плоскости
поперечного
сечения
и
параллельны
оси
О
Y (
узкой
стенке
),
в
то
время
как
магнитные
линии
образуют
замкнутые
контуры
в
продольной
плоскости
.
Силовые
линии
вектора
→
E
проводятся
наиболее
густо
в
середине
широкой
стенки
(
my
E
•
=0
максимальна
при
2
a
x = )
и
разрежаются
при
приближении
к
краям
стенки
(
my
E
•
=0
при
x=0; a).
В
поперечной
34
плоскости
силовые
линии
магнитного
поля
параллельны
оси
ОХ
(
широкой
стенке
)
и
прово
-
дятся
равномерно
(
my
H
•
).
Так
как
n=0,
то
поле
вдоль
оси
О
Y
однородно
.
Волна
Н
10
имеет
наибольшую
критическую
частоту
,
поэтому
размеры
поперечного
сечения
волновода
,
при
которых
возможна
передача
энергии
на
заданной
частоте
,
для
этой
волны
будут
наименьшими
.
Использование
волны
Н
10
позволяет
уменьшить
габариты
и
мас
-
су
волновода
,
а
,
следовательно
,
и
его
стоимость
.
Поляризация
электрического
поля
волны
Н
10
линейна
и
строго
фиксирована
,
что
обычно
требуется
для
работы
ряда
устройств
и
сис
-
тем
СВЧ
тракта
.
Рис
.9 –
Структура
поля
волны
Н
10
в
прямоугольном
волноводе
Благодаря
этим
достоинствам
основная
волна
прямоугольного
волновода
Н
10
имеет
большое
значение
для
технического
применения
.
Прямоугольный
волновод
с
волной
Н
10
широко
используется
в
качестве
фидерных
линий
в
радиорелейных
,
радиолокационных
и
других
системах
сантиметрового
диапазона
волн
.
Каждому
типу
волны
в
волноводе
соответствует
своя
структура
поверхностных
токов
на
идеально
проводящих
стенках
.
Плотность
поверхностного
тока
определяется
по
формуле
:
=
→→→
Hnj
S
,
, (69)
где
→
n
-
внешняя
нормаль
к
поверхности
волновода
.
Используя
эту
формулу
и
известное
распределение
магнитного
поля
,
легко
построить
картину
поверхностных
токов
для
любого
типа
волны
в
волноводе
.
В
случае
Е
-
волн
Н
Z
=0
и

35
поверхностный
ток
имеет
только
продольные
составляющие
.
На
стенках
волновода
с
Н
-
волнами
существуют
и
поперечный
,
и
продольный
токи
.
11. Ослабление волн при распространении в волноводе
В
реальных
волноводах
часть
энергии
волны
тратится
на
нагревание
стенок
и
потери
в
диэлектрике
,
который
заполняет
волновод
.
Вследствие
этого
амплитуда
поля
уменьшается
вдоль
направления
распространения
,
т
.
е
.
волна
затухает
.
Уменьшение
амплитуд
векторов
по
-
ля
происходит
по
экспоненциальному
закону
z
e
α
−
,
где
α
-
коэффициент
затухания
.
Так
как
изменение
мощности
Р
,
переносимой
электромагнитной
волной
вдоль
оси
О
Z,
пропорцио
-
нально
квадрату
изменения
амплитуды
поля
,
то
z
ePzP
α
2
0
)(
−
= , (70)
где
0
P –
мощность
в
сечении
z=0
направляющей
системы
.
Найдем
величину
мощности
потерь
,
приходящихся
на
единицу
длины
волновода
z
P
z
zzPzP
P
z
n
∂
∂
−=
∆
∆
+
−
=
→∆
)()(
lim
11
0
/
. (71)
Подставляя
(71)
в
(70),
находим
:
)(22
2
0
/
zPePP
z
n
αα
α
==
−
,
т
.
е
.α=
)(2
/'
zP
P
п
. (72)
С
другой
стороны
коэффициент
ослабления
прд
ααα
+= ,
где
д
α
–
коэффициент
ос
-
лабления
в
диэлектрике
,
заполняющем
волновод
,
пр
α
-
коэффициент
ослабления
в
проводя
-
щих
стенках
волновода
.
Величина
д
α
определяется
как
)(tg
k
д
δβ
α
2
2
= .
Обычно
прд
αα
<< ,
поэтому
α ≈
пр
α
.
Для
нахождения
пр
α
выделим
участок
волновода
длиной
∆
z.
Мощность
потерь
в
стенках
волновода
на
этом
участке
равна
:
∫ ∫∫
∆
∆
=
∆
=∆
∆
Г Г
mm
z
п
dlH
z
dlHdzP
2
0
2
0
0
/
||
2
||
2
1
σσ
, (73)
где
Г
-
контур
поперечного
сечения
волновода
.
Из
(72)
следует
,
что
потери
на
единицу
длины
равны
:
∫
∆
=
Г
mп
dlHP
2
0
/
||
2
1
σ
. (74)
Подставляя
(74)
в
(72)
получаем
:
пр
α
=
∫
Г
m
S
dlH
zP
R
2
||
)(4
, (75)
где
R
S
-
активная
часть
поверхностного
сопротивления
,
равная
36
σ
µπ
σ
a
S
f
R =
∆
=
0
1
. (76)
Так
как
для
всех
металлов
,
кроме
ферромагнитных
0
µµ
≈
а
,
то
3
10987.1
−
⋅≈
σ
f
R
S
Ом
. (77)
Отметим
,
что
формула
(77)
справедлива
не
только
для
прямоугольного
волновода
,
но
и
для
расчета
коэффициента
ослабления
в
проводящих
стенках
любой
волноводной
линии
передачи
.
Для
волны
Н
10
в
прямоугольном
волноводе
общая
формула
(75)
преобразуется
в
более
простую
вида
2
2
)2/(1
])2/()/(21[
abZ
aabR
c
S
λ
λ
α
−
×+
= . (78)
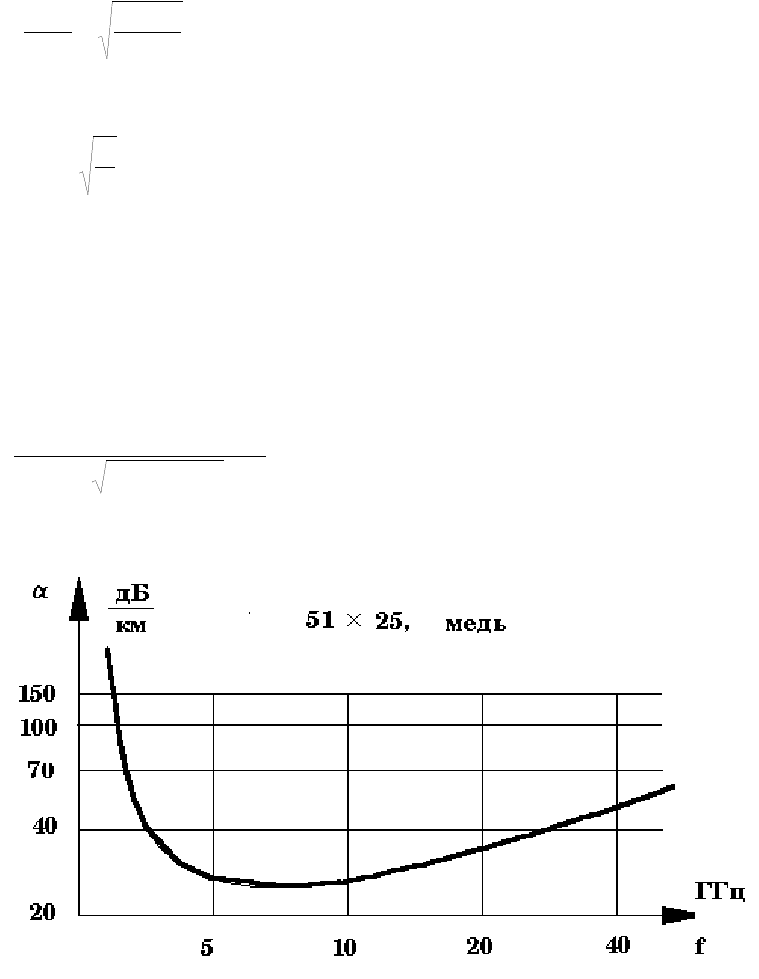
График
зависимости
коэффициента
ослабления
от
частоты
в
этом
случае
изображен
на
рис
.10
Рис
.10 –
Частотная
зависимость
коэффициента
ослабления
волны
Н
10
Из
графика
видно
,
что
потери
в
стенках
волновода
резко
возрастают
при
приближении
частоты
к
критической
.
Это
вызвано
резким
увеличением
локальных
переотражений
волны
от
стенок
волновода
.
Рост
α
на
частотах
f>>f
кр
объясняется
усилением
поверхностного
эф
-
фекта
на
стенках
.
Это
ограничивает
применение
металлических
волноводов
на
очень
высо
-
ких
частотах
,
в
частности
,
в
диапазоне
миллиметровых
и
более
коротких
длин
волн
.
Выбор
размеров
поперечного
сечения
волновода
.
К
линии
передачи
любого
типа
предъявляются
следующие
требования
:
обеспечение
одноволнового
режима
работы
,
высо
-
кая
электрическая
прочность
,
малое
затухание
волны
,
минимально
возможные
габариты
.
Выполнение
этих
требований
обеспечивается
правильным
выбором
размеров
поперечного
сечения
.

37
12. Направляемые волны в круглом металлическом волноводе
Круглый
волновод
в
цилиндрической
системе
координат
изображен
на
рис
.11.
Волны
в
круглом
волноводе
обозначаются
mn
E
и
mn
H .
Их
поля
имеют
более
сложную
зависимость
от
попе
-
речных
координат
по
сравнению
с
волнами
в
прямоугольном
волноводе
.
Радиальная
зависимость
поля
описывается
функциями
Бесселя
m-
го
порядка
J
m
(
γ
⊥
,r)
и
их
первыми
производными
'
m
J (γ
⊥
,r).
Индексы
m
и
n
в
обозначении
волн
имеют
следующий
смысл
: m-
число
стоячих
полуволн
,
укладывающихся
вдоль
ок
-
ружности
волновода
, n-
число
стоячих
полуволн
,
укладывающихся
вдоль
радиуса
волновода
.
Ниже
приведены
формулы
для
всех
компонент
поля
Е
-
волн
и
Н
-
волн
в
круглом
волноводе
:
Е
-
волны
( 0=
•
mx
H ).
)zi(
m
zm
e))(mcos()r(JEE
⋅−
⊥
•
−=
β
ϕϕγ
00
,
,e))(mcos()r(JE
i
H
,e))(msin()r(JE
r
mi
H
,e))(msin()r(JE
r
im
E
,e))(mcos()r(JE
i
EE
)zi(/
m
a
m
)zi(
m
a
rm
)zi(
m
m
)zi(/
m
rm
⋅−
⊥
⊥
•
⋅−
⊥
⊥
•
⋅−
⊥
⊥
•
⋅−
⊥
⊥
•
−
−
=
−
−
=
−=
−
−
=
β
ϕ
β
β
ϕ
β
ϕϕγ
γ
ωε
ϕϕγ
γ
ωε
ϕϕγ
γ
β
ϕϕγ
γ
β
00
00
2
00
2
000
(79)
где
Е
0
–
амплитуда
продольной
составляющей
вектора
,
напряженности
электрического
поля
на
оси
волновода
,
ϕ
0
–
начальная
фаза
поля
.
Н
-
волны
( 0=
•
mx
H ).
)(
00
))(cos()(
zi
m
zm
emrJHH
⋅−
⊥
•
−=
β
ϕϕγ
,e))(mcos()r(JH
i
E
,e))(msin()r(JH
r
mi
E
)zi(/
m
a
m
)zi(
m
a
rm
⋅−
⊥
⊥
•
⋅−
⊥
⊥
•
−=
−=
β
ϕ
β
ϕϕγ
γ
ωµ
ϕϕγ
γ
ωµ
00
00
2
(80)
.e))(msin()r(JH
r
im
H
,e))(mcos()r(JH
i
H
)zi(
m
m
)zi(/
m
rm
⋅−
⊥
⊥
•
⋅−
⊥
⊥
•
−=
−
−
=
β
ϕ
β
ϕϕγ
γ
β
ϕϕγ
γ
β
00
2
00
Величина
λ
кр
для
волн
mn
E
и
mn
H
определяется
из
таблицы
вида
:
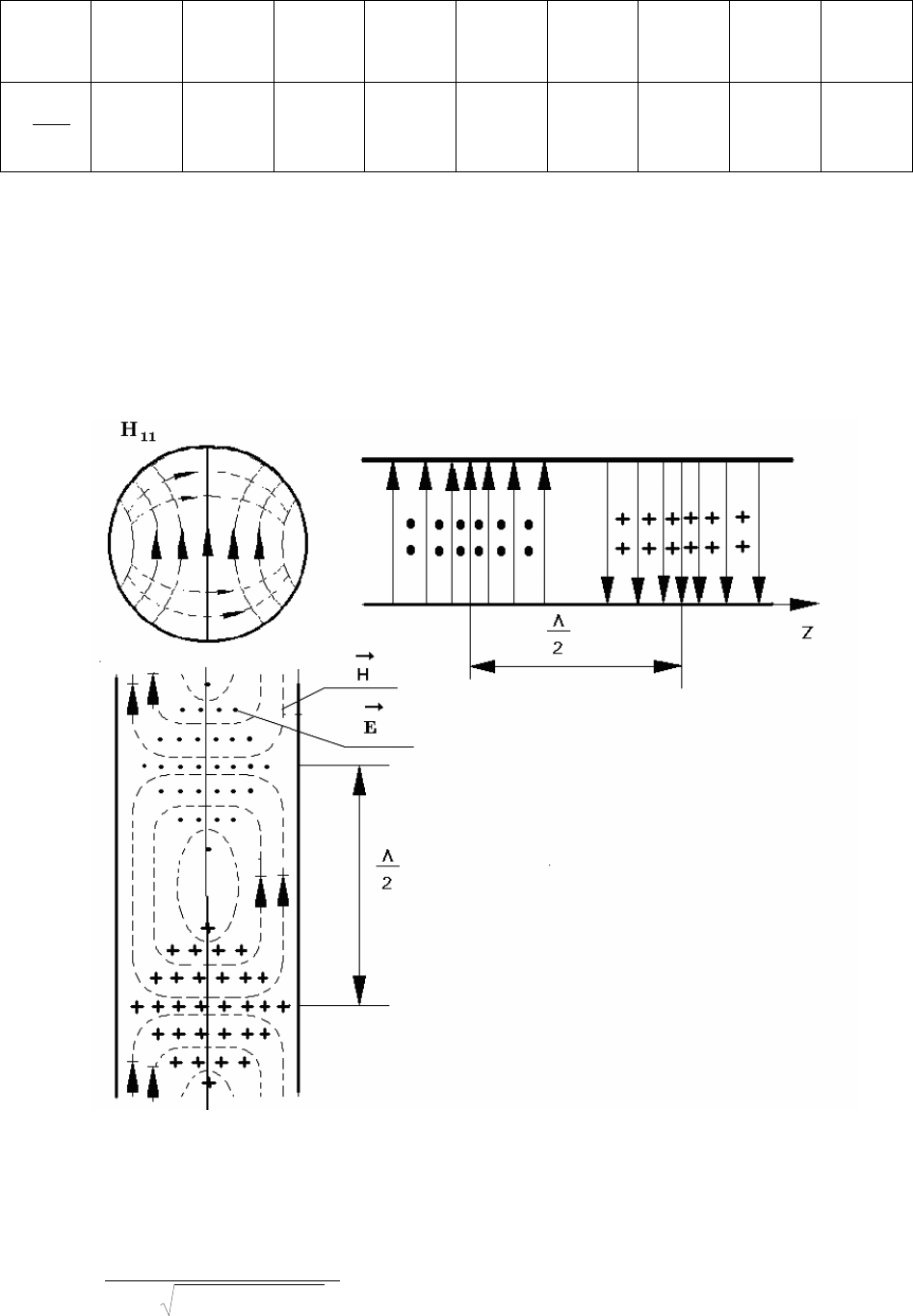
Рис
.11 -
Круглый
волновод
38
Тип
волн
ы
H
11
E
01
H
21
H
01
E
11
H
31
E
21
H
41
H
12
а
кр
λ
3.413 2.613 2.06 1.64 1.64 1.5 1.223 1.182 1.178
Волны
Н
01
и
Е
11
имеют
одинаковые
значения
λ
КР
.
Эти
волны
,
а
также
волны
Н
02
и
Е
12
,
Н
03
и
Е
13
и
т
.
д
.
являются
вырожденными
.
Основной
волной
круглого
волновода
является
волна
H
11
.
Структура
силовых
линий
изображена
на
рис
.12.
Условие
одноволнового
режима
имеет
вид
2.613 a <
λ
< 3.413a,
и
пото
-
му
радиус
волновода
нужно
выбирать
из
соотношения
0.293
λ
<
а
< 0.383
λ
.
Рис
.12 –
Структура
поля
основной
волны
круглого
волновода
Коэффициент
ослабления
основной
волны
круглого
волновода
определяется
по
формуле
2
2
)413.3/(1
])413.3/(418.0[
aRZ
aR
c
s
λ
λ
α
−
+
= . (81)
Графики
зависимости
α
от
частоты
для
волн
Н
11
,
Е
01
и
Н
01
круглого
волновода
представ
-
лены
на
рис
. 13.
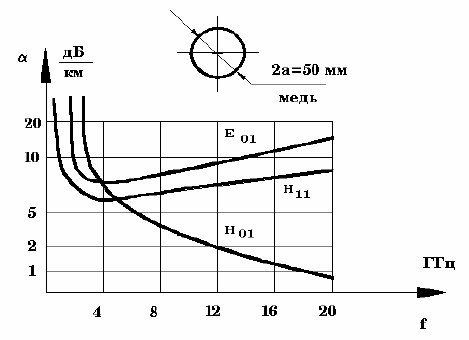
39
Рис
.13 –
Частотная
зависимость
коэффициентов
ослабления
в
круглом
волноводе
Применение
круглых
волноводов
с
волной
Н
11
в
качестве
протяженных
фидерных
трак
-
тов
ограничивается
ее
поляризационной
неустойчивостью
.
Эта
особенность
волны
Н
11
состоит
в
появлении
составляющей
поля
с
паразитной
ортогональной
поляризацией
,
которая
возникает
из
-
за
эллиптичности
поперечного
сечения
волновода
,
вызванной
неточностью
изготовления
,
деформацией
и
изгибами
волновода
.
Из
коротких
отрезков
волновода
с
волной
Н
11
выполня
-
ются
различные
устройства
СВЧ
тракта
:
поляризаторы
,
фазовращатели
,
циркуляторы
и
др
.
Отрезки
круглых
волноводов
с
волной
Е
01
,
обладающей
осесимметричной
структурой
поля
,
используются
во
вращающихся
сочленениях
волноводов
.
Большой
практический
интерес
представляет
осесимметричная
волна
Н
01
,
коэффициент
ослабления
которой
с
ростом
частоты
неограниченно
падает
,
что
свидетельствует
о
том
,
что
волна
Н
01
способна
с
малыми
потерями
переносить
энергию
на
большие
расстояния
.
Практическое
использование
волны
Н
01
связано
со
значительными
трудностями
,
так
как
волна
весьма
чувствительна
к
деформации
волновода
,
поскольку
асимметрия
стенок
приводит
к
появлению
других
типов
волн
–
низших
,
а
на
очень
высоких
частотах
–
высших
типов
.
При
этом
аномальные
свойства
частотной
зависимости
по
-
терь
в
волноводе
могут
быть
утрачены
.
Кроме
того
,
паразитные
типы
волн
образуют
попутный
поток
,
наличие
которого
приводит
к
искажению
сигнала
.
13. Линии передачи с Т-волной
Полагая
в
формулах
связи
0==
••
mzmz
HE ,
получаем
,
что
0
2
=
⊥
⊥
•
→
γ
m
E
и
0
2
=
⊥
⊥
•
→
γ
m
H
Эти
равенства
справедливы
при
отличных
от
нуля
поперечных
составляющих
поля
Т
-
волны
,
если
γ
⊥
=0.
При
этом
условии
λ
кр
=∞
и
f
кр
=0.
В
линиях
передачи
,
допускающих
существование
Т
-
волны
,
эта
волна
может
распространяться
на
любой
частоте
.
Параметры
Т
-
волны
не
зависят
от
частоты
и
равны
параметрам
в
свободном
пространстве
.
Дисперсия
в
линиях
передачи
с
Т
-
волной
отсутствует
.

40
Коаксиальный
волновод
(
кабель
).
На
рис
.14
коаксиальный
волновод
изображен
в
ци
-
линдрической
системе
координат
.
Волны
в
коаксиальном
волно
-
воде
обозначаются
mn
E
и
mn
H ,
причем
смысл
индексов
m
и
n
тот
же
,
что
и
у
волн
в
круглом
волноводе
.
Наличие
внутреннего
про
-
водника
приводит
к
существованию
Т
-
волны
,
которая
является
ос
-
новной
,
т
.
к
.
∞=
Т
кр
λ
.
Для
нахождения
структуры
Т
-
волны
в
коак
-
сиальном
кабеле
используется
следующий
подход
.
Полагая
в
вол
-
новых
уравнениях
0
2
=
⊥
•
γ
mz
E
и
0
2
=
⊥
•
γ
mz
H
получаем
:
0
2
=∇
⊥
→
•
m
E
и
0
2
=∇
⊥
→
•
m
H . (82)
Уравнения
(82)
представляют
собой
двумерные
уравнения
Лапласа
.
Поле
,
удовлетво
-
ряющее
уравнению
Лапласа
,
является
потенциальным
.
Это
означает
,
что
решение
первого
из
уравнений
(82)
может
быть
выражено
через
градиент
некоторой
скалярной
функции
:
m
Е
⊥
→
•
=-grad
⊥
ψ
, (83)
где
функция
ψ
-
является
скалярным
потенциалом
,
также
удовлетворяющим
уравнению
Лап
-
ласа
:
•
⋅∇
ψ
2
= 0. (84)
Аналогичное
представление
для
вектора
m
H
⊥
•
→
через
градиент
некоторой
функции
мож
-
но
не
находить
,
поскольку
вектора
m
E
⊥
•
→
и
m
H
⊥
•
→
выражаются
друг
через
друга
следующим
об
-
разом
:
]E,z[H
a
m
•
→→
⊥
•
→
=
β
ωε
, (85)
т
.
е
.
векторы
m
E
⊥
•
→
и
m
H
⊥
•
→
у
Т
-
волны
взаимно
ортогональны
.
В
полярной
системе
координат
,
которую
удобно
использовать
при
нахождении
струк
-
туры
поля
в
коаксиальном
волноводе
,
уравнение
(84)
имеет
вид
:
0
11
2
2
22
2
=
∂
∂
+
∂
∂
+
∂
∂
ϕ
ψψψ
r
rr
r
. (86)
При
решении
этого
уравнения
необходимо
учитывать
,
что
на
поверхности
внутреннего
проводника
и
на
внутренней
поверхности
внешнего
проводника
должны
выполняться
гранич
-
ные
условия
,
т
.
е
.
касательная
компонента
вектора
→
E
должна
обращаться
в
ноль
.
Решение
уравнения
(86),
удовлетворяющее
граничным
условиям
:
)(
10
)ln(
zi
m
erR
Е
⋅−
•
⋅−=
β
ψ
, (87)
Рис
.14
