Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions

Подождите немного. Документ загружается.

100 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

to create four annular diffuser passages allows this large increase in volume

to be achieved without any increase in overall combustor length.

3.7.4 Vortex-Controlled Diffuser

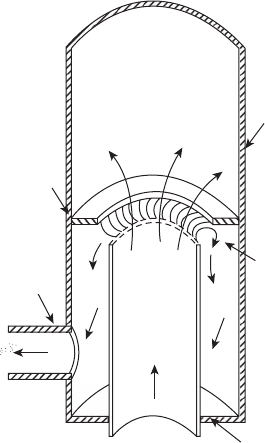
The notion of achieving rapid and efcient diffusion by boundary-layer

bleed at the throat of a sudden expansion has been studied by Adkins [38]. A

tubular version of his VCD is sketched in Figure 3.13. The basic mechanism

of vortex control is not yet fully understood, but Adkins has proposed a

model that is best described by reference to Figure 3.14. According to this

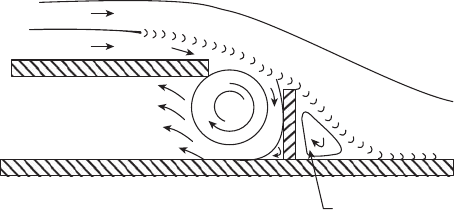
model, the application of external suction causes the static pressure inside

the vortex chamber to fall below that of the main stream. In consequence,

stream a, which is being drawn into the vortex, experiences considerable

acceleration. On the other hand, stream b, which ows down the diffuser, is

owing into a region of greater static pressure and therefore decelerates. A

shearing action, produced by the velocity differential between the streams,

then results in the creation of an extremely turbulent layer that inhibits ow

separation.

The experiments indicate that diffusion is achieved in a very short length

(clearly advantageous for aircraft applications) and the effectiveness is almost

Secondary duct

Vortex

Primary duct

Bleed duct

Fence

Figure 3.13

Vortex-controlled diffuser of tubular conguration. (From Adkins, R.C., Journal of Fluids

Engineering, 297–302, 1975. With permission.)

Diffusers 101

equal to the theoretical optimal value. Tests have also conrmed that the

technique can be applied to conical, annular, and two-dimensional in con-

gurations. The air-bleed requirements depend mainly on area ratio; most

combustor applications, the bleed amounts to about 4% of the mainstream

ow. As with most diffusers, under some conditions the ow can become

unstable. Adkins and Yost [39] have described the instabilities that occur

when the optimum area ratio is exceeded and have derived empirical equa-

tions for predicting the optimum area ratio, the level of pressure recovery,

and the bleed-air requirement, all of which are governed by the degree of

nonuniformity of the inlet velocity prole.

Some features of the VCD are not yet fully resolved, such as the design of the

suction slot and the location of the vortex retaining fence. Also, the trade-off

between suction rate and diffuser length, as it affects static-pressure rise, total-

pressure loss, and exit ow stability, warrants further study. However, suf-

cient work has already been done to demonstrate its considerable potential

for application to gas turbines, and especially to high-temperature engines

in which bleed air from the combustor is required to cool the hot sections

downstream. It offers signicant savings in engine length and weight, com-

bined with an increase in available liner pressure drop, which could improve

almost all aspects of combustion performance.

3.7.5 Hybrid Diffuser

The main drawback of the VCD is its high bleed-off requirement. To sur-

mount this problem, Adkins et al. [39–41] developed a hybrid concept that

combines a VCD with a conventional wide-angled postdiffuser located at its

exit. Hybrid systems of this type have been demonstrated successfully by

Juhasz and Smith [42,43] and Verdouw [44]. Figure 3.15 shows a hybrid con-

cept of Adkins et al. [40]. In this design, the vortex-controlled step accounts

for only a small increase in cross-sectional area, thus requiring only a mini-

mal bleed-off. The turbulent layer generated by the step is then used to

Coanda bubble

Stream ‘b’

Stream ‘a’

Vortex

chamber

Figure 3.14

Flow mechanisms of vortex control. (From Adkins, R.C., Matharu, D.S., and Yost, J.D., Journal of

Engineering for Power, 103, 229–36, 1981. With permission.)

102 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

inhibit ow separation from a relatively wide-angled conventional diffuser

that contains a much greater part of the overall increase in area. The results

obtained for an overall area ratio of 2 and an inlet Mach number of 0.25 are

shown in Figure 3.16. This gure also contains corresponding performance

data for a conventional conical diffuser of the same area ratio. The superior

performance of the hybrid arrangement is very evident from this gure.

Another impressive feature of the hybrid diffuser is its ability to yield

high pressure recovery, even without the application of bleed. This is dem-

onstrated in Figure 3.16 where, at zero bleed, the hybrid diffuser is shown

to produce pressure recoveries far greater than the equivalent conventional

conical diffuser. Thus, the benets of the new diffuser can be demonstrated

either as an increase in pressure recovery of at least 25% over that of a con-

ventional diffuser of the same length, or as the attainment of the same recov-

ery in a much shorter length. For example, to achieve a value for C

of 0.52, a

conventional diffuser needs twice the length of a hybrid diffuser.

The ability to achieve high pressure recoveries in a short length with small

amounts of bleed would appear to make the hybrid diffuser very attractive

for gas turbine applications. Unfortunately, it cannot be used on most engines

because the pressure of the bleed air is too low for turbine blade cooling.

A solution to this problem is to t a short prediffuser to the upstream end

of the VCD, as shown in Figure 3.17. Only a small area ratio of around 1.3–1.4

is needed to raise the bleed air pressure to a level that is sufcient for turbine

cooling [44,45]. The main diffusion takes place downstream in either a VCD

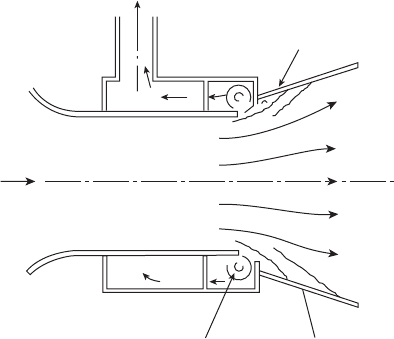
Bleed air

Turbulent

shear layer

Supply air

Vortex controlled

diﬀuser

Wide angled

conventional

diﬀuser

Figure 3.15

Hybrid diffuser arrangement. (From Adkins, R.C., Matharu, D.S., and Yost, J.D., Journal of

Engineering for Power, 103, 229–36, 1981. With permission.)

Diffusers 103

or hybrid diffuser. The main drawback to a prediffuser is the additional

length required.

The results obtained from various VCD and hybrid diffusers, with and without

prediffusers, have been reviewed and summarized by Klein [9]. More detailed

performance data may be found in the publications of Adkins et al. [39–41].

Conventional

diffuser, AR = 2.0

Hybrid diﬀuser

overall area ratio = 2.0

V.C.D. area ratio = 1.34

0.1

L/D

0.2

0.3

0.4

0.5

0.6

Figure 3.16

Comparison of hybrid and conventional diffuser performance. (From Adkins, R.C., Matharu,

D.S., and Yost, J.D., Journal of Engineering for Power, 103, 229–36, 1981. With permission.)

Combustor

Prediffuser

Vortex

Figure 3.17

VCD tted with prediffuser. (From Adkins, R.C., “Tests on a Vortex-Controlled Diffuser

Combined with a Pre-Diffuser and Simulated Combustor,” Craneld SME Report No.

C1331-D2, Craneld University, November 1975.)

104 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

In summary, hybrid-diffuser geometries have amply demonstrated their

potential to improve performance and reduce length. According to Klein [9],

future research should employ compressor-generated inlet conditions and

inlet velocity proles with different spanwise peak locations.

The relative merits of faired, dump, and VCDs are summarized in

Table 3.1.

3.7.6 Diffusers for Tubular and Tuboannular Combustors

With tubular combustors, the diffuser also serves as a transition piece, con-

verting from an annular segment at the compressor outlet to a circular sec-

tion at the combustor casing. The geometry is almost always complex, and

pressure losses tend to be high. Normally, a hollow snout is tted to the liner

dome. The snout should be designed to ensure smooth deceleration of the

ow into the annulus.

For tuboannular (or can-annular) combustors, the normal arrangement

includes a settling length that terminates in a conventional annular diffuser

of modest area ratio, say about 1.5. This is followed by a dump chamber if

TABLe 3.1

Relative Merits of Various Diffuser Types

Diffuser Type Merits Drawbacks

Aerodynamic or faired Low pressure loss Relatively long

Performance susceptible to

thermal distortion and

manufacturing tolerances

Performance and stability

sensitive to variations in inlet

velocity prole

Dump Relatively short

Insensitive to variations

in inlet ow

conditions

Pressure loss about 50% higher

than for faired type

Vortex-controlled High performance

Short length

Low pressure loss

Requires minimum of 4% air bleed

Design procedures not fully

established

Hybrid High performance

Short length

Low pressure loss

Low bleed air

requirement

Design procedures not fully

established

Bleed air pressure too low for

turbine cooling

Hybrid with

prediffuser

High performance

Low pressure loss

Low bleed air

requirement

High bleed air pressure

Needs extra length

Diffusers 105

length is at a premium, or by a snout-combustor conguration if further

diffusion is required to minimize the loss in total pressure.

Potentially, the tuboannular conguration has many advantages over the

annular one. According to Adkins and Binks [46] they include:

1. A superior aerodynamic ow pattern inside the combustor liner.

Here, the air jets ow radially through the liner wall to meet the

radially expanding fuel spray, thereby ensuring good matching

between the air and fuel ows. As a result, the combustion process

is more homogeneous, giving smaller quantities of exhaust gas pol-

lutants and a more uniform temperature distribution, both around

the combustor liner and at turbine inlet. It follows that cooling air

can be used more efciently.

2. A smaller diameter liner gives improved mechanical rigidity with-

out the need for expensive cooling devices, such as machined rings.

Stress levels are lower, and these allow either a higher liner tempera-

ture or a longer life.

3. Combustor development can be accomplished by tests on single

cans, thereby using only a fraction of the total engine airow.

In practice, these potential advantages are rarely achieved because of the

unsatisfactory condition of the ow between the combustor casing and the

liners. The large diameter of the liners, relative to the duct height at the com-

pressor exit, dictates that the divergence angle of the diffuser greatly exceeds

the maximum permissible angle for good aerodynamic stability. This causes

the ow to adhere to only one of the diffuser walls—usually the outer wall—

with the result that most of the compressor efux is directed to the radially

outboard regions of the combustor. Some of this air ows radially inward

through the spaces between liners and then ows upstream along the inner

casing to create a large recirculatory ow pattern. The end result is that some

of the air entering the liner is supplied from the normal downstream direc-

tion, whereas the remaining air is supplied from the reverse direction. This

destroys the symmetry of the liner airow distribution, which leads to exces-

sive exhaust smoke and other problems associated with poor combustion

performance.

A method for greatly improving the aerodynamics of tuboannular com-

bustors by the use of a novel diffusion system termed the “wedge diffuser”

has been described by Adkins and Binks [46].

3.7.7 Testing of Diffusers

It is important that the initial diffuser design be tested while the engine is

still at an early stage of development. Water ow-visualization rigs are ide-

ally suited for this purpose and, when properly used, will clearly reveal any

irregularities in the ow. It is important to simulate the compressor discharge

106 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

conditions as closely as possible, in terms of velocity prole and angle of

swirl. To this end, it is helpful to incorporate a set of compressor-outlet guide

vanes at the diffuser inlet. The presence of swirl in the compressor efux

precludes the use of sectors for most test purposes, which means that ow

visualization studies on diffusers for annular combustors require full-scale,

fully annular models.

As discussed below, computational uid dynamics (CFD) simulations can

also provide valuable guidance in the diffuser design and development stages.

3.8 Numerical Simulations

Adkins et al. [12,13] have developed relatively simple calculation methods for

designing optimum annular diffusers. Potential ow computations have also

been used successfully; one example being in the design of a two-passage

diffuser for the NASA/GE “Energy Efcient Engine.” The main advantage

of these methods is simplicity, but they are not suited to the complex geom-

etries and ow conditions of some modern combustor diffusers.

Advances in computer technology have led to the increasingly widespread

use of CFD for calculating ow elds throughout the combustor, including the

diffuser. Diffuser calculations do not have the problems of two-phase ows

and chemical reactions, but they do involve regions of adverse pressure gra-

dients, developing boundary layers, ow recirculation, and strong streamline

curvature. Other complications arise from the complex geometry of diffusers

and the presence in the ow of burner feed arms and liner support struts.

Klein [9] has reviewed the merits and drawbacks of various CFD simu-

lations as published in the literature, most of which are based on the k-ε

model of turbulence. Shyy [47,48] has also compared various numerical

schemes employed in a CFD application to a dump diffuser congura-

tion. Special importance is attached to the generation of the computational

grid. The orthogonal Cartesian or cylindrical grids used in the simulation

of ows in simple geometries cannot be applied to combustor diffusers

because they cannot predict the ow behavior near the walls. This means

that a boundary-tted curvilinear, non-orthogonal coordinate system must

be used. Also, the grid distribution must include very ne meshes in regions

where large gradients of the ow properties normal to the ow direction

could exist. Any available experimental evidence on the ow elds in such

regions could clearly provide useful guidance in the selection of mesh shape

and the number of grid nodes [47–49].

The k-ε model is well established, relatively cheap, and easy to use. Its draw-

back in diffuser applications is that it predicts the ow to remain attached in

situations where experiments indicate separation [50]. Another shortcoming

of the model arises in ows containing high strain rates produced by strong

Diffusers 107

curvature. Their effects are known to be poorly predicted by eddy viscosity

models [51]. An alternative to the use of such models is to derive transport

equations for the Reynolds stresses themselves. This approach adds appre-

ciably to the cost and complexity of the computations, but it is far superior to

the k-ε model for predicting ows in regions of strong curvature.

Jones and Manners [52] used the k-ε model to compute the ow in a faired

diffuser that had previously been subjected to extensive experimental study

by Stevens et al. [53,54]. The model was found to overpredict the velocity near

the concave wall. Velocity proles were poorly predicted in many regions of

the ow. The overall pressure recovery was also grossly overpredicted. These

discrepancies between computation and experiment were attributed to de-

ciencies of the k-ε model. Many other workers, including Shyy [48], Koutmos

and McGuirk [49], Mayer and Kneeling [55], and Ando et al. [56], have tested

the accuracy of the k-ε model by comparing static pressure recoveries and/

or velocity proles for a number of different geometries, including split and

dump diffusers. The k-ε model gave erroneous results in all cases.

Despite their shortcomings, CFD methods have been shown to predict the

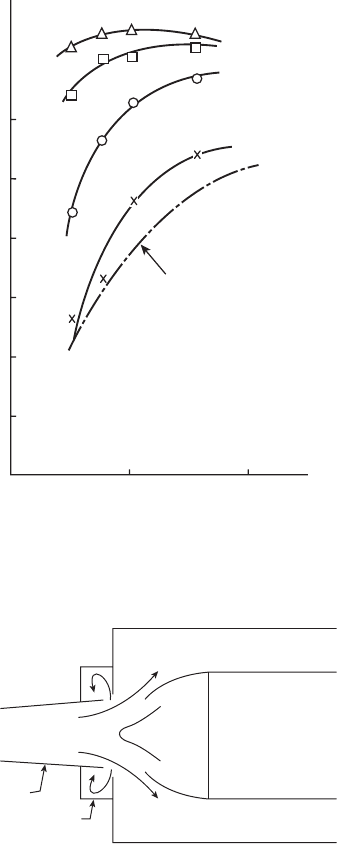
gross features of diffuser ows quite well. This is illustrated in Figure 3.18

Figure 3.18

Comparison of computed and visualized ow elds in a dump diffuser. (From Hestermann, R.,

Kim, S., Ben Khaled, A., and Witting, S., Journal of Engineering for Gas Turbines and Power, 117(4),

686–94, 1995. With permission.)

108 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

f r om Reference [2 3], wh i c h sh ows a co mpa r i s on bet we e n co mpu ted (k-ε model)

and visualized ow elds in a two-dimensional dump diffuser. Flow visu-

alization was achieved using a hydrogen bubble technique on a water table.

The level of agreement between the ow-visualization method and the

numerical simulation, as illustrated in Figure 3.18, is clearly very satisfac-

tory. Hestermann et al. [23] and Zhiben and Guangshi [57] obtained good

agreement between computed and measured velocity proles at the exits of

annular and two-dimensional prediffusers, respectively. Furthermore, Karki

et al. [58], using the high Reynolds number form of the k-ε model, obtained

useful insight into the highly three-dimensional nature of combustor dif-

fuser ows. Their results showed signicant asymmetric effects in the ow

due to the presence of support struts and fuel nozzles.

The conclusion to be drawn from these various studies is that the k-ε model

is incapable of predicting pressure recoveries with any degree of accuracy,

but can provide a good representation of velocity proles in the absence of

strong curvature.

Many other examples to illustrate the value of numerical methods in pre-

dicting the gross features of diffuser ow elds have been presented by Klein

[9]. Developments in CFD methods have now reached a stage at which they

are an important tool in diffuser design. They can even provide details of

three-dimensional ows, which experimental methods cannot reveal. Their

main limitation is their inability to predict diffuser performance, which is

due to deciencies in the k-ε models currently used. As more powerful com-

puters become available, the greater accuracy of the Reynolds stress model

in predicting ow elds and pressure losses in regions of strong curvature

should enable it to become an important tool in diffuser design.

Nomenclature

A geometrical area

AR area ratio (A

)

pressure recovery coefcient

maximum pressure recovery coefcient in a prescribed length

maximum pressure recovery coefcient in a prescribed area ratio

liner depth

liner depth ratio

dump gap width

dump gap ratio

h annulus height

L wall length



mass ow rate

Diffusers 109

N axial length

P total pressure

ΔP loss in total pressure across diffuser

p static pressure

q dynamic pressure (ρu

/2)

R radius, conical diffusers

outer radius

inner radius

ΔR annulus height (R

–R

)

u velocity

W width (distance between divergent walls) of two-dimensional

diffusers

ρ density

η overall effectiveness

θ half-divergence angle

λ loss coefcient

Subscripts

1. diffuser inlet plane

2. diffuser outlet plane

Other

— mean value, mass-ow derived

References

1. Sovran, G., and Klomp, E. D., “Experimentally Determined Optimum Geometries

for Rectilinear Diffusers with Rectangular, Conical or Annular Cross Section,”

in G. Sovran, ed., Fluid Mechanics of Internal Flow, Elsevier, Amsterdam, pp. 270–

319, 1967.

2. Kline, S. J., Abbott, D. E., and Fox, R. W., “Optimum Design of Straight-Walled

Diffusers,” Journal of Basic Engineering, Vol. 81, pp. 321–31, 1959.

3. Howard, J. Η. G., Thornton-Trump, A. B., and Henseler, H. J., “Performance and

Flow Regimes for Annular Diffusers,” ASME Paper 67-WA/FE-21, 1967.

4. McDonald, A. T., and Fox, R. W., “An Experimental Investigation of

Incompressible Flow in Conical Diffusers,” International Journal of Mechanical

Science, Vol. 8, pp. 125–39, 1966.

5. Reneau, L. R., Johnston, J. P., and Kline, S. J., “Performance and Design of

Straight, Two-Dimensional Diffusers,” Journal of Basic Engineering, Vol. 95,

pp. 141–50, 1967.

6. Cockrell, D. J., and King, A. L., “A Review of the Literature on Subsonic Fluid

Flow through Diffusers,” The British Hydromechanics Research Association,

TN 902, 1967.