Латышева М.А. Эконометрическое моделирование неравенства социально-экономического развития регионов РФ
Подождите немного. Документ загружается.


21
образом.
Основные направления федеральной региональной политики должны
основываться на:
– обеспечении равных конкурентных условий в хозяйственной
деятельности, определении условий предоставления государственной
помощи;
– создании равных возможностей для развития предпринимательской
деятельности с обеспечением доступа к инфраструктуре;
– повышении эффективности программно-целевых методов прямой
государственной поддержки;
– усилении процесса межрегиональной интеграции и улучшении
качества экономического пространства;
– обеспечении геостратегических интересов страны.
Именно за счет мобилизации активности российских регионов и
повышения эффективности использования их ресурсов возможно провести
социально-экономические преобразования.
Одной из стратегических целей региональной политики Российской
Федерации на данном этапе развития страны является обеспечение
глобальной конкурентоспособности России и ее регионов. Достижение
данной цели направлено:
- в первую очередь на обеспечение эффективной интеграции регионов
в мировой рынок, ускорение социально-экономического развития
Российской Федерации за счет правильного распределения
производительных сил по территории, развития системы расселения и
повышения связанности страны, что должно открыть доступ территорий и их
населения к источникам социально- экономического роста;
- на развитие инфраструктурной базы социально-экономического роста
территорий;
- на формирование конкурентоспособных в глобальном масштабе
территориальных производственных кластеров;

22
- на обеспечение перехода к поляризованному развитию и создание
нового пространственного каркаса страны из «опорных регионов».
Система федерального мониторинга региональных социально-
экономических показателей предполагает:
• оценку уровня социально-экономического развития регионов,
муниципальных образований, в зависимости от их функции в
пространственной организации страны. Введение системы статистики для
городских округов и городских поселений. Новая система показателей
должна позволять проводить оценку инфраструктурных возможностей для
реализации крупных инвестиционных проектов в регионах и муниципальных
образованиях, выявление формальных и неформальных барьеров для ведения
бизнеса (в том числе формирования конкурентоспособных экономических
кластеров) и осуществления инвестиционных проектов, объективную оценку
необходимости федеральной поддержки региона или муниципального
образования;
• оценку деятельности региональных органов власти по
проведению социально-экономических, бюджетной и административной
реформ, сбор информации и анализ состояния нормативно-правовой базы на
региональном и местном уровнях;
• оценку состояния трудового, демографического и миграционного
балансов территорий.
Анализ социально-экономического развития субъектов РФ
свидетельствует о неоднородности хозяйственного пространства России, а
значит, и с различиями возможностей успешной работы в рыночных
условиях. В выигрышном положении находятся в основном регионы-
экспортеры продукции, использующие устойчивый внешний спрос на нефть,
газ, цветные металлы и алмазы, а также крупные торгово-посреднические
центры и центры банковского капитала — Москва и Санкт-Петербург.
Поэтому государственная экономическая политика не должна основываться
на установлении общих для всех субъектов Федерации финансово-

23
экономических правил. Необходим объективный и конструктивный подход к
формированию государственной системы регулирования территориального
социально-экономического развития страны, основанный, во-первых, на
признании необходимости учета региональной специфики при выработке
экономической, социальной, финансовой политики государства. Во-вторых,
— на принятии обоснованных мер господдержки различных типов регионов,
имеющих общие проблемы и схожие особенности социально-
экономического развития, непосредственно влияющие на характер и
результаты хозяйственной деятельности.
5
Учет отмеченных выше особенностей поможет обеспечить повышение
благосостояния населения и сглаживание социально-экономического
развития регионов РФ.
1.2. Методы оценки неравенства в уровне социально-экономического
развития регионов РФ
Простейшие статистические характеристики дифференциации
Для анализа неравенства в уровне социально-экономического развития
регионов Российской Федерации часто используют простейшие
характеристики дифференциации, которые измеряют вариацию различных
социально-экономических показателей. К ним относятся:
• дисперсия и среднеквадратическое отклонение;
• коэффициент вариации и его модификации;
• коэффициенты концентрации, в т.ч. индекс энтропии Тейла;
• асимметрия и куртозис (эксцесс).
Первые две группы представляют собой показатели дифференциации,
характеризующие разброс наблюдений вокруг среднего, третья группа
5
Ушаков, А. Разработка прогнозов социально-экономического развития регионов с
использованием комплексной имитационной модели / А. Ушаков [и др.] // Российский
экономический журнал – 2000. – № 2. – С. 72-78.

24
описывает концентрацию наблюдений, а последняя - степень отклонения
выборочного распределения от нормального.
Для анализа неравенства социально-экономических показателей
помимо представленных можно использовать и такую простую
описательную статистику, как отношение максимального и минимального
значений:
i
i
min
max
. К недостаткам данного индекса относится то, что он не
показывает характер неравенства в развитии регионов: вызвано ли оно
большой вариацией в развитии всех регионов или наличием нескольких
регионов, развитие которых значительно отличается от развития остальных
регионов. Поэтому указанная характеристика не отражает реальный разброс
регионов, а показывает лишь амплитуду колебаний, то есть имеет косвенное
отношение к дифференциации.
Относительное отклонение от среднего значения
P
P
xx=R
i
i
i
, где Р
i
–численность населения для региона i, P –
численность населения в целом в РФ. Относительное отклонение от среднего
значения показателя развития используется в литературе для оценки
неравномерностей пространственного развития достаточно давно (Каквани,
1980).
6
Одно из его преимуществ состоит в значительно меньшей, чем у
коэффициента вариации, чувствительности к выбросам.
Дисперсия и среднеквадратическое отклонение
7
Дисперсия является вторым центральным моментом:
n
=i
i
)x(x
n
=XVar
1
2
1
)( . Дисперсия и стандартное отклонение (корень из
дисперсии) характеризуют среднее отклонение от среднего значения
выборки. Дисперсию трудно интерпретировать содержательно. Однако
стандартное отклонение хорошо поддается интерпретации. И потому, среди
этих двух величин наиболее важное значение имеет стандартное отклонение.
6
Доклад по оценке бедности в Российской Федерации. - 2004. - 268 с.
7
Сизова Т.М. Статистика: Учебное пособие. - СПб.: Спб ГУИТМО, 2005. - 80 с.

25
Это значение можно представить как среднее расстояние, на котором
находятся элементы от среднего элемента выборки. Стандартное отклонение
имеет ту же размерность, что и исследуемый признак и показывает,
насколько хорошо среднее значение описывает всю выборку.
Если выборка подчиняется стандартному нормальному закону
распределения, то около 68% значений выборки будут находиться в рамках
одного стандартного отклонения от среднего значения и около 95% будут
находиться в рамках двух стандартных отклонений.
Существенным недостатком дисперсии и стандартного отклонения,
ограничивающим их применение для анализа дифференциации, является
наличие размерности и зависимость от масштаба, которые не позволяют
проводить сравнения для показателей, имеющих разные единицы измерения.
Коэффициент вариации
Коэффициент вариации позволяет оценить вариации в развитии всех
регионов РФ. Он является производным от стандартного отклонения и не
имеет размерности, т.е. он обладает сходной информативностью, но
позволяет проводить сравнения между разными показателями. Тем самым, у
коэффициента вариации есть существенное преимущество перед дисперсией
и стандартным отклонением. Следовательно, для измерения регионального
неравенства предпочтительнее использовать коэффициент вариации. В
самом простом случае коэффициент вариации является отношением
стандартного отклонения к среднему:
x
XVar
=VarK
)(
. Одна из сложностей
использования коэффициента вариации состоит в том, что его значение
чувствительно к количеству регионов различного размера в стране. Для
решения указанной проблемы можно воспользоваться взвешенным
коэффициентом вариации W, в формуле которого учтен «вес» каждого
региона в численности населения страны.

26
Таким образом, взвешенный коэффициент вариации Уильямсона
является модификацией коэффициента вариации:
x
P
P
xx
W
i
i
i
2
, где
Р
i
- население региона i, P – население страны в целом. Особенность этого
показателя заключается во взвешивании каждого региона по численности
населения. Его применение оправдано для исследования российских
регионов, где размах вариации числа жителей составляет до сотни раз
(Москва и небольшие автономные округа, например, Чукотский). Это
позволяет снизить влияние богатых малонаселенных регионов (например,
ХМАО) и повысить значимость бедных регионов центральной России.
Коэффициенты концентрации
Коэффициенты концентрации представляют собой достаточно
большую группу показателей, среди которых можно выделить:
Квинтильные и децильные коэффициенты концентрации;
Коэффициент Джини;
Коэффициент концентрации Герфиндаля;
Индексы энтропии, в т.ч. индекс энтропии Тейла.
Первая группа показателей характеризует соотношение средних
значений исследуемого признака внутри сравниваемых крайних групп
регионов или их доли в общем объеме. Чаще всего такие коэффициенты
рассчитываются для квинтильных (20%) и децильных (10%) групп по
формуле:
q
q
d
d
d
=qK
1
, где
q
d - q % квантиль распределения, a q=10% для
децильного коэффициента и 20% для квинтильного. К их недостаткам
относится индифферентность к фактическому количеству числа объектов,
находящихся на полярных полюсах по уровню исследуемых признаков.
Коэффициент Джини является комплексной характеристикой
концентрации. Основой для расчета индекса Джини является построение
кривой Лоренца. Эта кривая представляет собой графическое изображение

27
кумулятивного распределения, в котором кумулируются количество
регионов и доля ВРП в ВВП. В прямоугольной системе координат кривая
Лоренца является выпуклой вниз и проходит под диагональю единичного
квадрата с координатами: (0;0); (0,1); (1;1) и (1;0). Теоретическая
возможность абсолютно равного распределения ВРП представлена
биссектрисой, которая указывает на то, что каждый регион получает
одинаковый ВРП. Это значит, что если 20, 40, 60 % регионов получают
соответственно 20,40,60 % от всего ВВП, то соответствующие точки будут
расположены на биссектрисе. Область между линией абсолютного равенства
и кривой Лоренца указывает на степень неравенства ВРП: чем больше эта
область, тем больше степень неравенства ВРП. Если бы фактическое
распределение ВРП было абсолютно равным, то кривая Лоренца и
биссектриса совпали бы.
Рис. 1. Кривая Лоренца
Степень неравномерности распределения графически можно выразить
через площадь, заключенную между диагональю квадрата и кривой Лоренца,
отнесённой к площади треугольника. Указанное соотношение и получило
название индекса (коэффициента) Джини. Чем выше полученное
соотношение, тем больше неравенство между регионами. Индекс Джини
определяет степень отклонения фактически сложившегося распределения
ВРП по регионам от линии их теоретически возможного равномерного
0
1
1
доля регионов
Доля ВРП в ВВП

28
распределения, комплексно характеризует процесс сосредоточения ВРП по
субъектам РФ. Коэффициент Джини – один из самых распространенных в
России показателей неравенства, вычисляется как
n
i
n
j
ji
k
k
xx
nn
x
n
=G
1
1
1
2
1
.
Взвешенный коэффициент Джини, который позволяет учитывать «вес»
каждого региона в численности населения страны:
P
P
P
P
xx
P
P
x
=G
j
i
n
i
n
j
ji
k
k
k
2
1
.
8
В случае близости индекса Джини к 1 имеется абсолютно
неравномерное распределение признака, т.е. его полная концентрация в
одних руках. Если же индекс Джини стремится к 0, то имеет место
абсолютно равномерное распределение и нулевая концентрация. К
преимуществам данного показателя относятся:
– комплексность и универсальность;
– возможность сравнения распределения признака в совокупностях с
различным числом единиц (например, регионы с разной численностью
населения);
– возможность отслеживать динамику неравномерности распределения
признака в совокупности на разных этапах.
Одним из недостатков коэффициента Джини является довольно частое
отсутствие описания группировки совокупности, то есть часто отсутствует
информация о том, на какие же именно квантили поделена совокупность.
Так, чем на большее количество групп поделена одна и та же совокупность
(больше квантилей), тем выше для нее значение коэффициента Джини.
9
8
Styme S., Jackson T. Intra-generational equity and sustainable welfare: a time series analyses
for the UK and Sweden // Ecological Economics, 2000, № 33, PP. 219-236.
9
Литвинов В.А. Концентрация и дифференциация денежных доходов по группам
населения Российской Федерации// Экономический журнал ВШЭ. 1999. №2. С. 226-237.

29
В общем виде, расчет коэффициента концентрации Герфиндаля
осуществляется по формуле:
n
=i
i
d=ПП
1
2
, где
i
d - доля каждой группы
населения (регионов) в общем значении исследуемого признака, i - номер
группы, n=i 1, . При стремлении числа групп к бесконечности его значение
стремится к 0. Когда есть только одна группа, его значение равно 1. При
неизменном количестве групп (числа исследуемых регионов), рост
коэффициента Герфиндаля в текущем периоде свидетельствует о повышении
концентрации и о росте неравенства. К преимуществам данного показателя
относятся простота его расчета, к недостаткам - достаточно низкая
информативность.
Перечисленные показатели, характеризуя концентрацию признака,
опосредовано отражают и общую меру дифференциации. Однако, при этом,
не стоит смешивать концентрацию, как сосредоточение чего-либо, с
дифференциацией, как различием между частями целого. Под
дифференциацией в статистике принято подразумевать отличие
варьирующего признака как взвешенной величины в крайних группах.
Следовательно, напрямую использовать указанные показатели для измерения
дифференциации нельзя.
Индекс энтропии Тейла, как и коэффициент Уильямсона, основан на
взвешивании по численности населения регионов:
I
=i
iii
PY
PY
Y
Y
=IT
1
/
/
ln , где
i
Y
- ВРП региона i, Y - сумма ВРП регионов страны,
i
P - население региона i, P
- население страны в целом. В случае абсолютного межрегионального
паритета IT принимает значение, равное нулю. По мере увеличения степени
межрегионального неравенства значение IT по модулю возрастает.
10
11
10
Мельников, Р.М. Анализ динамики межрегионального экономического неравенства:
зарубежные подходы и российская практика// Регион: экономика и социология. Т. 4. –
2005. - С. 3.
11
Theil H. Economics and information theory. – Amsterdam, 1967. – p. 121.
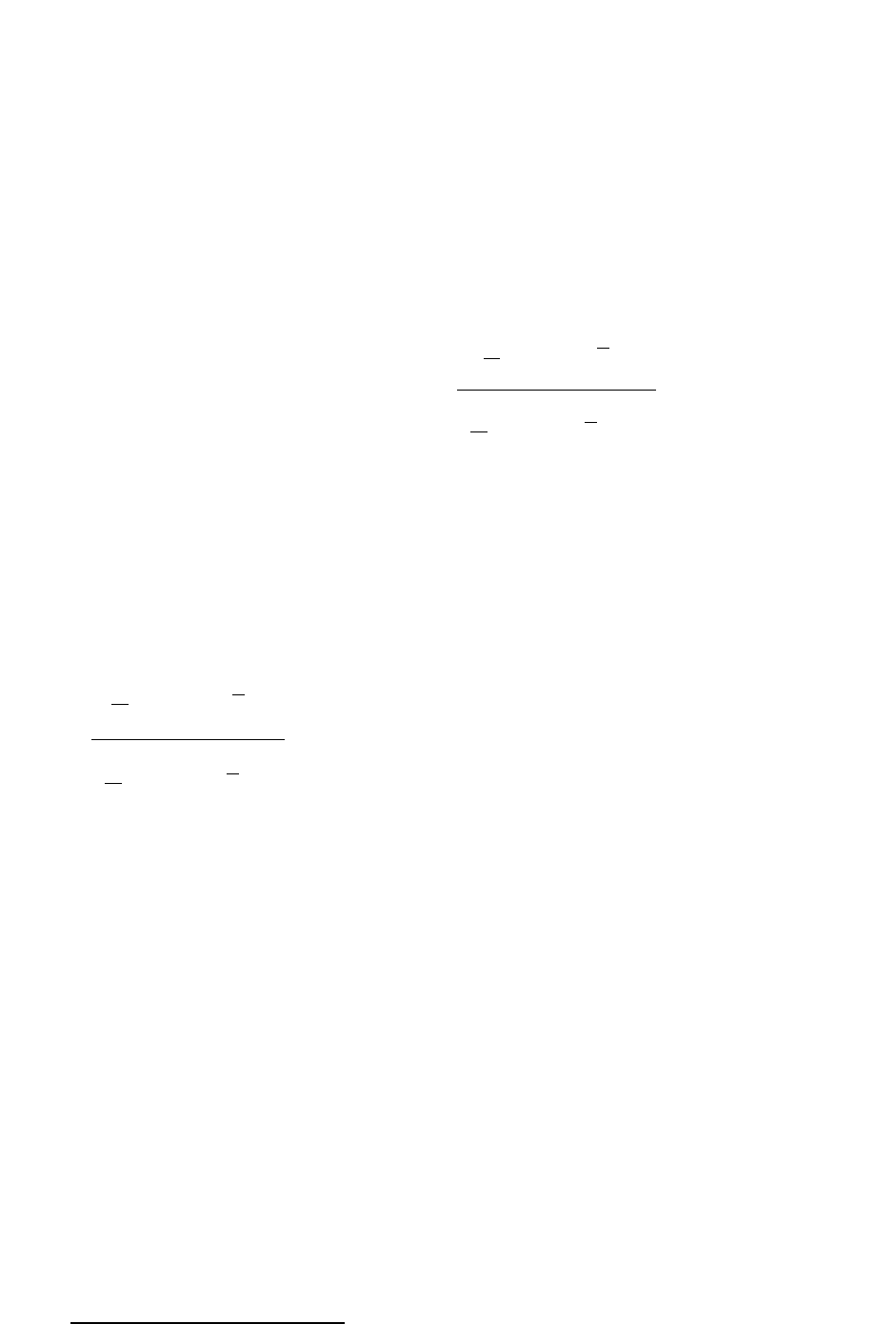
30
Преимущество данного индекса заключается в его независимости от
масштаба ВРП и численности населения, т.е. увеличение ВРП или населения
в одно и то же число раз не изменяет значение индекса.
Асимметрия и куртозис
Асимметрия и куртозис показывают меру отклонения выборочного
распределения от нормального. Асимметрия характеризует степень
скошенности вершины по сравнению с нормальным распределением: в
какую сторону и насколько.
3/2
1
2
1
3
n
1
1
n
=t
t
n
=i
i
xx
xx
n
=As
.
12
У нормального
распределения она равна 0. При отклонении вершины выборочного
распределения влево асимметрия принимает отрицательные значения, вправо
– положительные. Куртозис характеризует островершинность выборочного
распределения по сравнению с нормальным, у которого куртозис равен 3.
2
1
2
1
4
n
1
n
1
n
t=
t
n
=i
i
xx
xx
=Kurt .
13
Значения ниже 3 показывают сплюснутость
вершины, больше 3 - ее вытянутость. В отечественной статистике для
характеристики островершинности принято использовать показатель
эксцесса, отличающийся от куртозиса на 3 единицы (эксцесс=куртозис-3).
Куртозис, характеризуя островершинность выборочного
распределения, косвенно показывает и концентрацию наблюдений вокруг
модального значения (наиболее часто встречающегося). Чем ниже
островершинность, тем больше разброс, и выше неравенство. Асимметрия
характеризует концентрацию наблюдений с той или иной стороны от
среднего. Отрицательные значения асимметрии указывают на большее число
объектов, лежащих слева от среднего, положительные - справа, т.е. можно
12
Сизова Т.М. Статистика: Учебное пособие. - СПб.: Спб ГУИТМО, 2005. - 80 с.
13
Цыплаков А. В помощь изучающим эконометрику // Квантиль, №5, 2008 г. С. 41-56.
