Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)
Подождите немного. Документ загружается.

3
Аналогично дифракция в направлении оси Y даёт главные максимумы в
направлениях, определяемых условием
22
cos kd
. (2.3)
Поскольку углы , , – направляющие углы в декартовой системе координат, то для
них должно выполняться условие
1coscoscos
222
. (2.4)
Таким образом, получим
1coscoscos
cos
cos
222
22
11
kd
kd
, (2.5)
где k
1
, k
2
– целые числа, для заданной структуры с постоянными d
1
и d
2
.
Если задана волна длины , то можно из (2.5) определить значения углов , , , под
которыми наблюдаются главные максимумы света.
При изучении дифракции света удобнее бывает измерять не углы дифракции, а
расстояния между максимумами на экране и расстояние от экрана до решетки.
22
s in
lx
x
, (2.6)
где x – расстояние от центра экрана до точки наблюдения,
l – расстояние от экрана до решетки.
4
3 Экспериментальная часть
3.1 Приборы и принадлежности
1) Оптический квантовый генератор с блоком питания;
2) Оптическая скамья с экраном для наблюдения;
3) Мелкая сетка в держателе, используемая как двумерная дифракционная решетка.
3.2 Выполнение опыта
k
y
x, м
l, м
d
y
,м
d
yср
, м
d
y
,м
, %
1
0,005
1
1,2656*10
-4
1,2657*10
-4
1,27*10
-5
10,05
-1
-0,005
1,2656*10
-4
1,27*10
-5
10,05
2
0,01
1,2657*10
-4
6,39*10
-6
5,05
-2
-0,01
1,2657*10
-4
6,39*10
-6
5,05
3
0,015
1,2657*10
-4
4,28*10
-6
3,38
-3
-0,015
1,2657*10
-4
4,28*10
-6
3,38
2
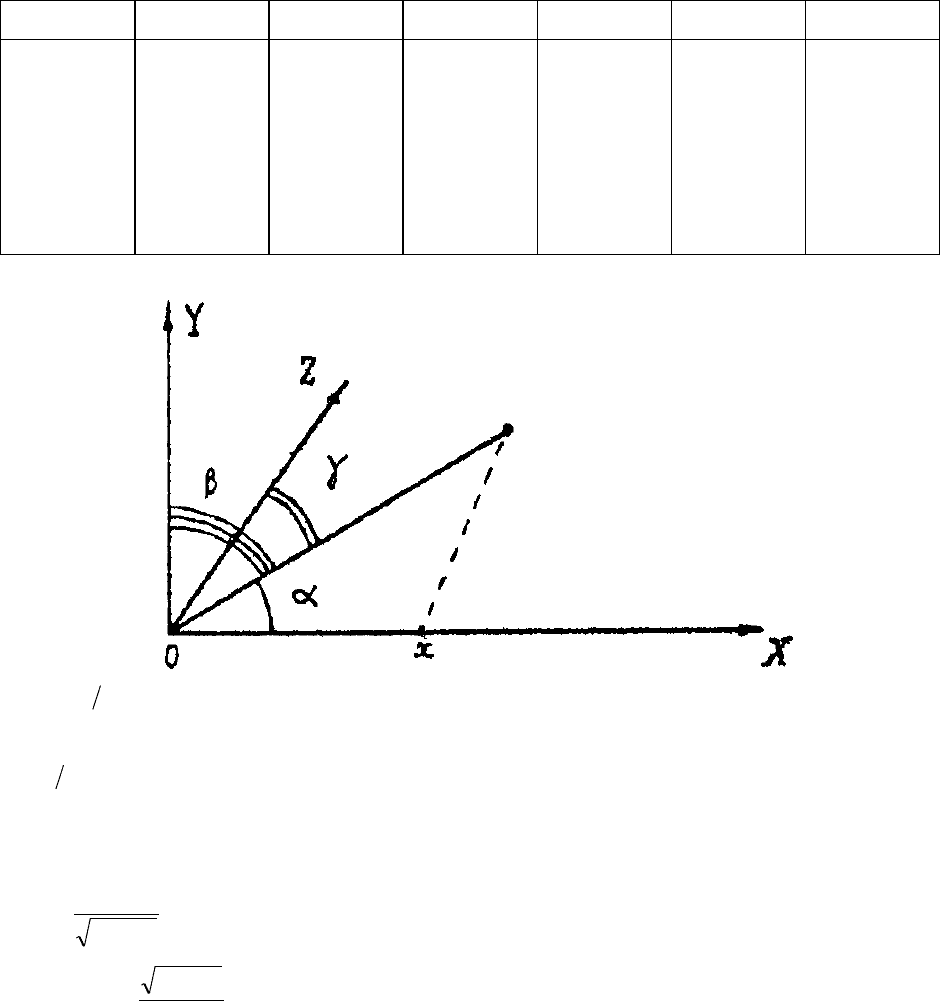
, откуда
cos = sin ;
2
;
z = l;
y
kdd sincos
11
;
22
s in
lx
x
;
x
lx
kdd
yy
22
1
(3.1)
Расчет погрешностей:
Для расчета погрешностей воспользуемся формулой
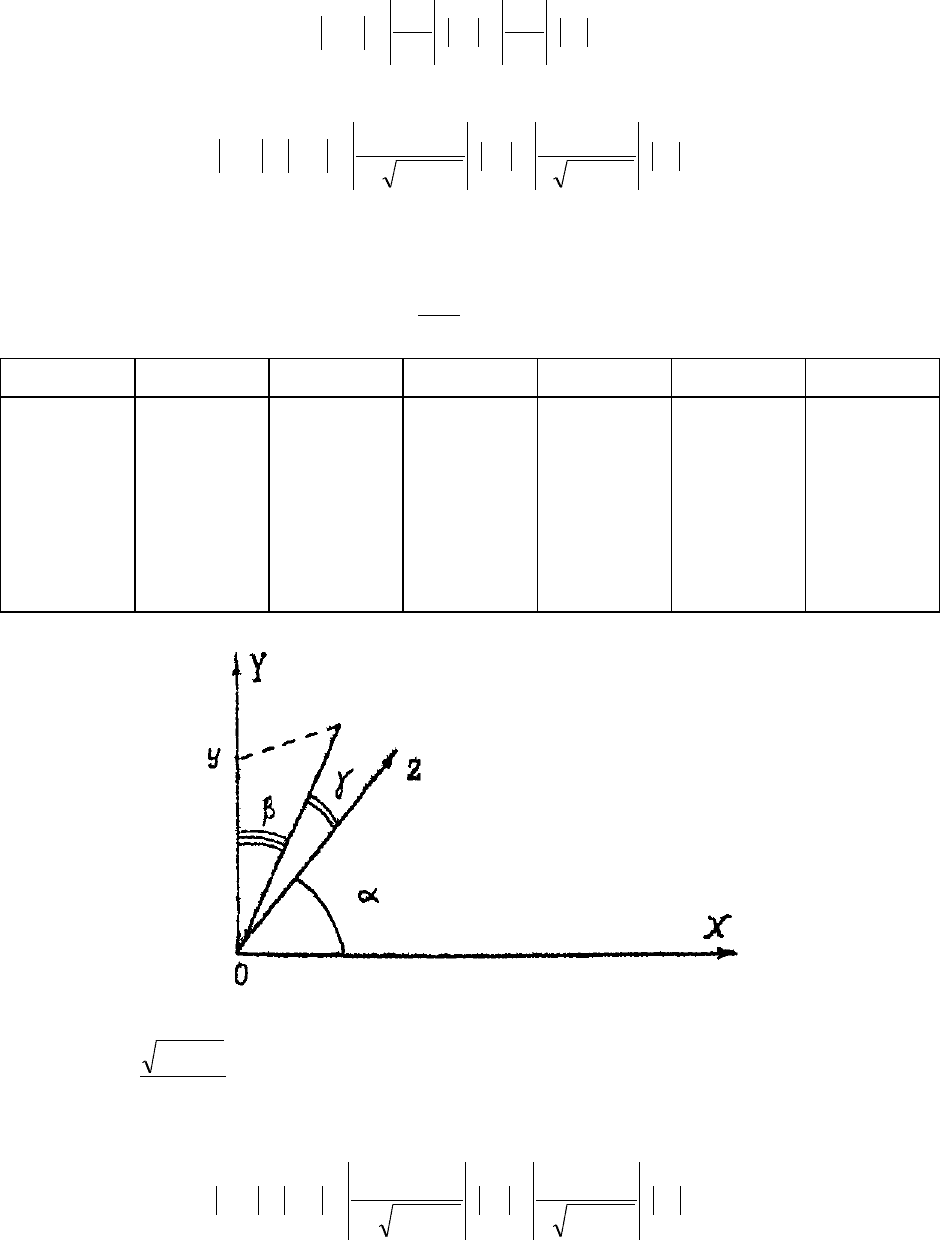
5
l
l
d
x
x
d
d
yy
y
. (3.2)
Из формулы (3.1) следует
l
lxx
l
x
lxx
l
kd
yy
22222
2
, (3.3)
где x = l = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
%100
y
y
d
d
. (3.4)
k
x
y, м
l, м
d
x
,м
d
xср
, м
d
x
,м
, %
1
0,005
1
1,2656*10
-4
1,2657*10
-4
1,27*10
-5
10,05
-1
-0,005
1,2656*10
-4
1,27*10
-5
10,05
2
0,01
1,2657*10
-4
6,39*10
-6
5,05
-2
-0,01
1,2657*10
-4
6,39*10
-6
5,05
3
0,015
1,2657*10
-4
4,28*10
-6
3,38
-3
-0,015
1,2657*10
-4
4,28*10
-6
3,38
Согласно рассуждениям из первой части опыта, аналогично получаем:
y
ly
kdd
xx
22
2
(3.5)
Из формул (3.2) и (3.5) получаем:
l
lyy
l
y
lyy
l
kd
xx
22222
2
, (3.6)
где y = l = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
6
%100
y
y
d
d
(3.7)
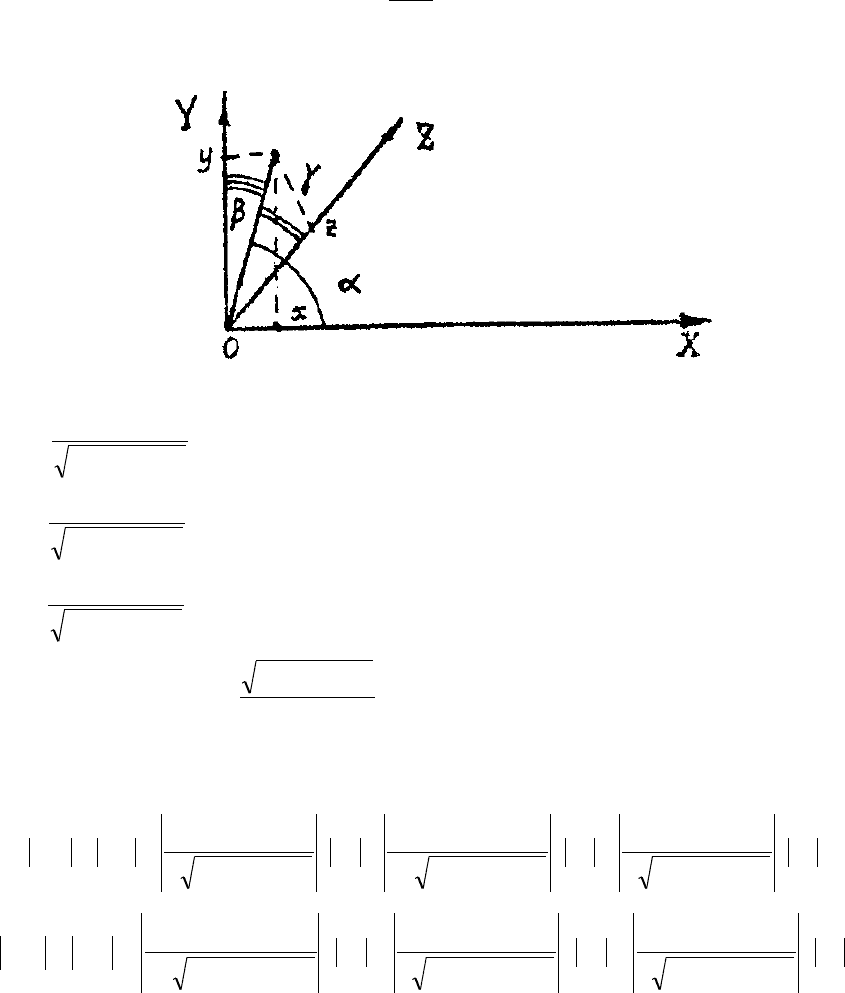
Для третьей части опыта:
z = l,
222
cos
zyx
x
,
222
cos
zyx
y
,
222
cos
zyx
z
,
x
zyx
kdkd
yyy
222
1
cos
(3.8)
(3.9)
Погрешности вычисляю по формулам:
z
zyxy
z
y
zyxy
zx
x
zyxy
x
kd
xx
2222222
22
222
(3.10)
z
zyxx
z
y
zyxx
y
x
zyxx
zy
kd
yy
2222222222
22
(3.11)
где x = y = z = 0,0005 м.
Относительные погрешности вычисляю по формуле, аналогичной (3.4) и (3.7).

k
x
k
y
x, м
y, м
l, м
d
x
, м
dy, м
d
xcp
, м
d
ycp
, м
d
x
, м
x
, %
d
y
, м
y
, %
1
2
0,005
0,01
1
6,33*10
-5
2,53*10
-4
1,27*10
-4
1,83*10
-4
3,20*10
-6
5,05
2,54*10
-5
10,05
-1
3
-0,005
0,015
4,22*10
-5
3,80*10
-4
1,43*10
-6
3,38
3,82*10
-5
10,05
2
-3
0,01
-0,015
8,44*10
-5
1,90*10
-4
2,86*10
-6
3,38
9,59*10
-6
5,05
-3
-2
-0,015
-0,01
1,90*10
-4
8,44*10
-5
9,59*10
-6
5,05
2,86*10
-6
3,38
2
-1
0,01
0,005
2,53*10
-4
6,33*10
-5
2,54*10
-5
10,05
3,20*10
-6
5,05
3
-3
0,015
-0,015
1,27*10
-4
1,27*10
-5
4,28*10
-6
3,38
4,28*10
-6
3,38
Вывод: в результате эксперимента были получены параметры двумерной дифракционной решетки (1,27*10
-4
м). Погрешность
составила не более 10%.
Уфимский государственный авиационный технический университет
Лабораторная работа №73
по курсу общей физики.
Изучение дифракции света на простейших преградах и дифракционной
решетке.
2
1 Цель работы
1.1 Ознакомление с дифракцией света на простейших преградах и дифракционной
решетке и теорией расчета дифракционной картины в этих случаях.
1.2 Экспериментальное определение длины волны излучения лазера с помощью
дифракционной решетки.
2 Теоретическая часть
Положение главных максимумов в дифракционной картине одномерной решетки в
случае нормального падения лучей определяется выражением:
kd sin
, (2.1)
где d – постоянная решетки,
– угол дифракции,
– длина световой волны,
k – целое число, определяющее порядок дифракционного максимума.
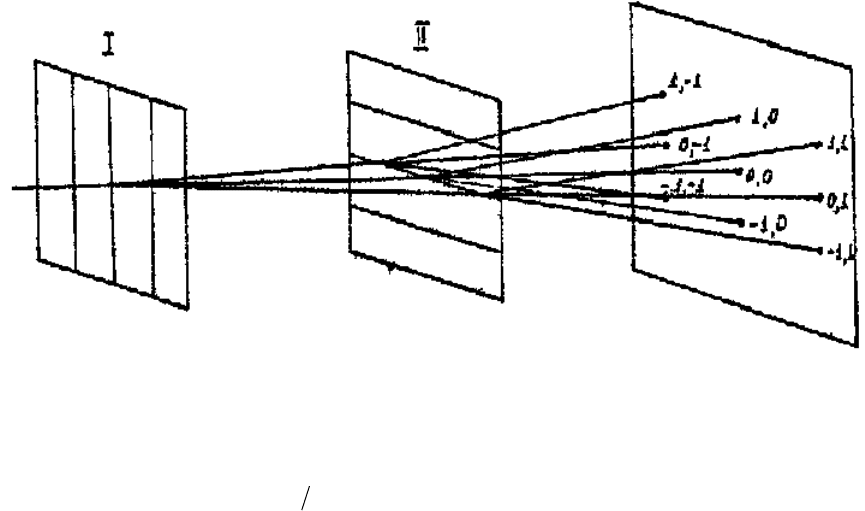
В простейшем случае двумерной дифракционной решеткой являются скрещенные
перпендикулярные решетки с периодами d
1
и d
2
. Дифракцию на такой решетке можно
рассматривать как последовательную дифракцию лучей на двух расположенных одна за
другой одномерных решетках с взаимно перпендикулярным расположением штрихов.
Узкий пучок монохроматического света, пройдя через первую решетку с вертикальными
штрихами, должен дать совокупность максимумов вдоль горизонтальной линии. Световой
пучок, соответствующий каждому максимуму, проходя через вторую решетку,
распадается на новую совокупность световых пучков, дающих максимумы вдоль
вертикальной линии.
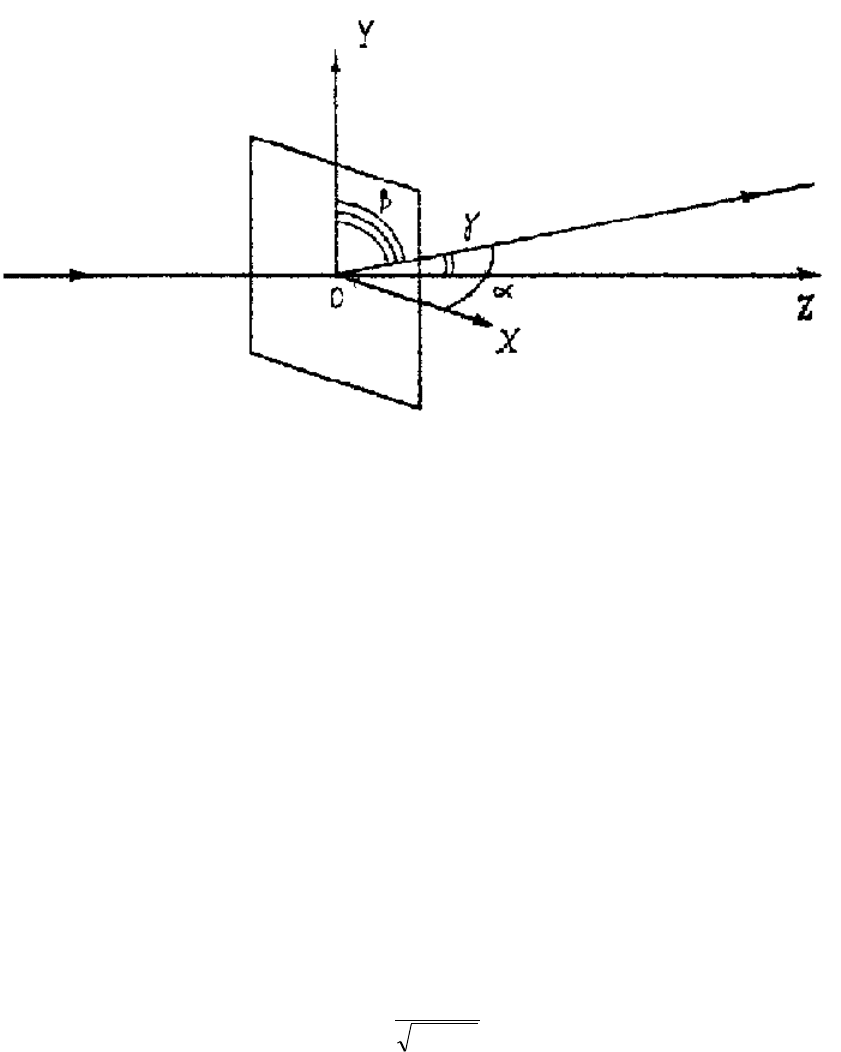
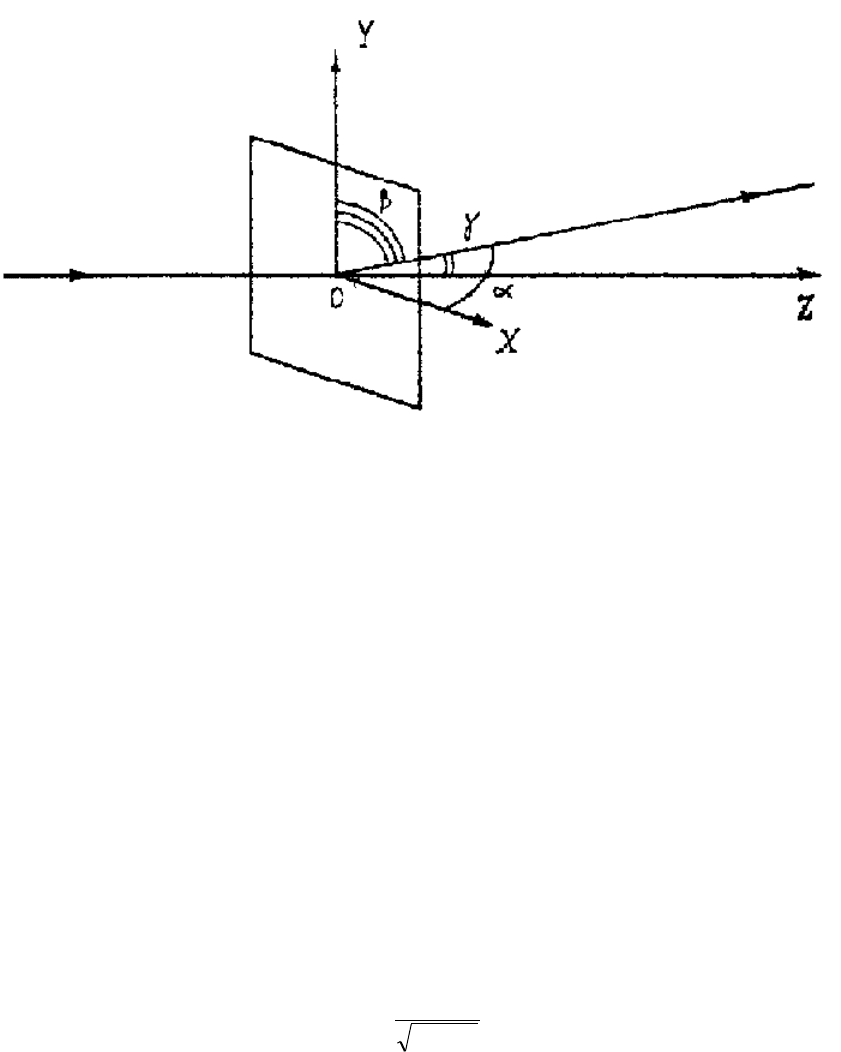
Пусть свет падает на решётку нормально. Выберем направление распространения
падающего луча за ось Z , а направления вдоль решёток – за оси Х и Y. Направление
падающего луча зададим углами
0
,
0
,
0
, а дифрагировавшего - углами , , (углы
между направлением луча и соответствующей координатной осью).
В нашем случае
2
00
,
0
= 0. Отклонение дифрагировавшего луча вдоль Х
приведет к образованию минимумов и максимумов света в зависимости от угла
дифракции . Используя теорию одномерной, решётки из условия главных максимумов в
данном случае получаем
3
11
cos kd
. (2.2)
Аналогично дифракция в направлении оси Y даёт главные максимумы в
направлениях, определяемых условием
22
cos kd
. (2.3)
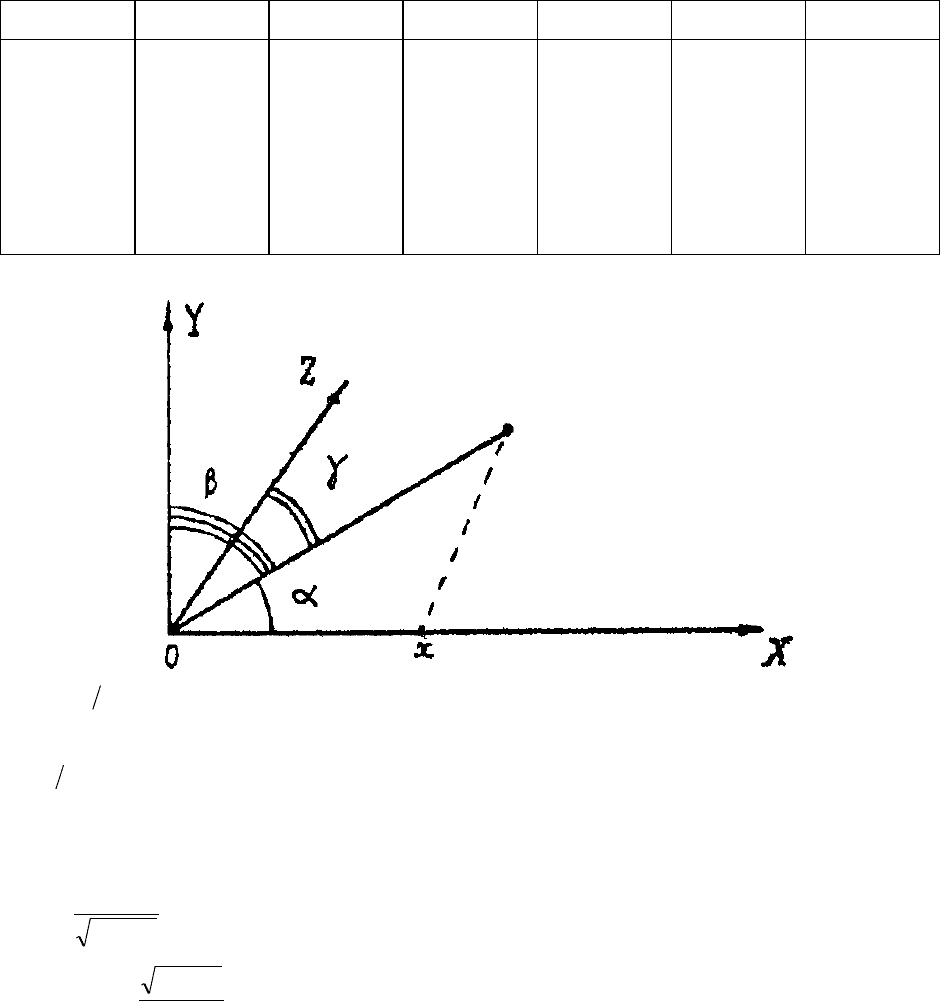
Поскольку углы , , – направляющие углы в декартовой системе координат, то для
них должно выполняться условие
1coscoscos
222
. (2.4)
Таким образом, получим
1coscoscos
cos
cos
222
22
11
kd
kd
, (2.5)
где k
1
, k
2
– целые числа, для заданной структуры с постоянными d
1
и d
2
.
Если задана волна длины , то можно из (2.5) определить значения углов , , , под
которыми наблюдаются главные максимумы света.
При изучении дифракции света удобнее бывает измерять не углы дифракции, а
расстояния между максимумами на экране и расстояние от экрана до решетки.
22
s in
lx
x
, (2.6)
где x – расстояние от центра экрана до точки наблюдения,
l – расстояние от экрана до решетки.
4
3 Экспериментальная часть
3.1 Приборы и принадлежности
1) Оптический квантовый генератор с блоком питания;
2) Оптическая скамья с экраном для наблюдения;
3) Мелкая сетка в держателе, используемая как двумерная дифракционная решетка.
3.2 Выполнение опыта
k
y
x, м
l, м
d
y
,м
d
yср
, м
d
y
,м
, %
1
0,005
1
1,2656*10
-4
1,2657*10
-4
1,27*10
-5
10,05
-1
-0,005
1,2656*10
-4
1,27*10
-5
10,05
2
0,01
1,2657*10
-4
6,39*10
-6
5,05
-2
-0,01
1,2657*10
-4
6,39*10
-6
5,05
3
0,015
1,2657*10
-4
4,28*10
-6
3,38
-3
-0,015
1,2657*10
-4
4,28*10
-6
3,38
2
, откуда
cos = sin ;
2
;
z = l;
y
kdd sincos
11
;
22
s in
lx
x
;
x
lx
kdd
yy
22
1
(3.1)
Расчет погрешностей:
Для расчета погрешностей воспользуемся формулой
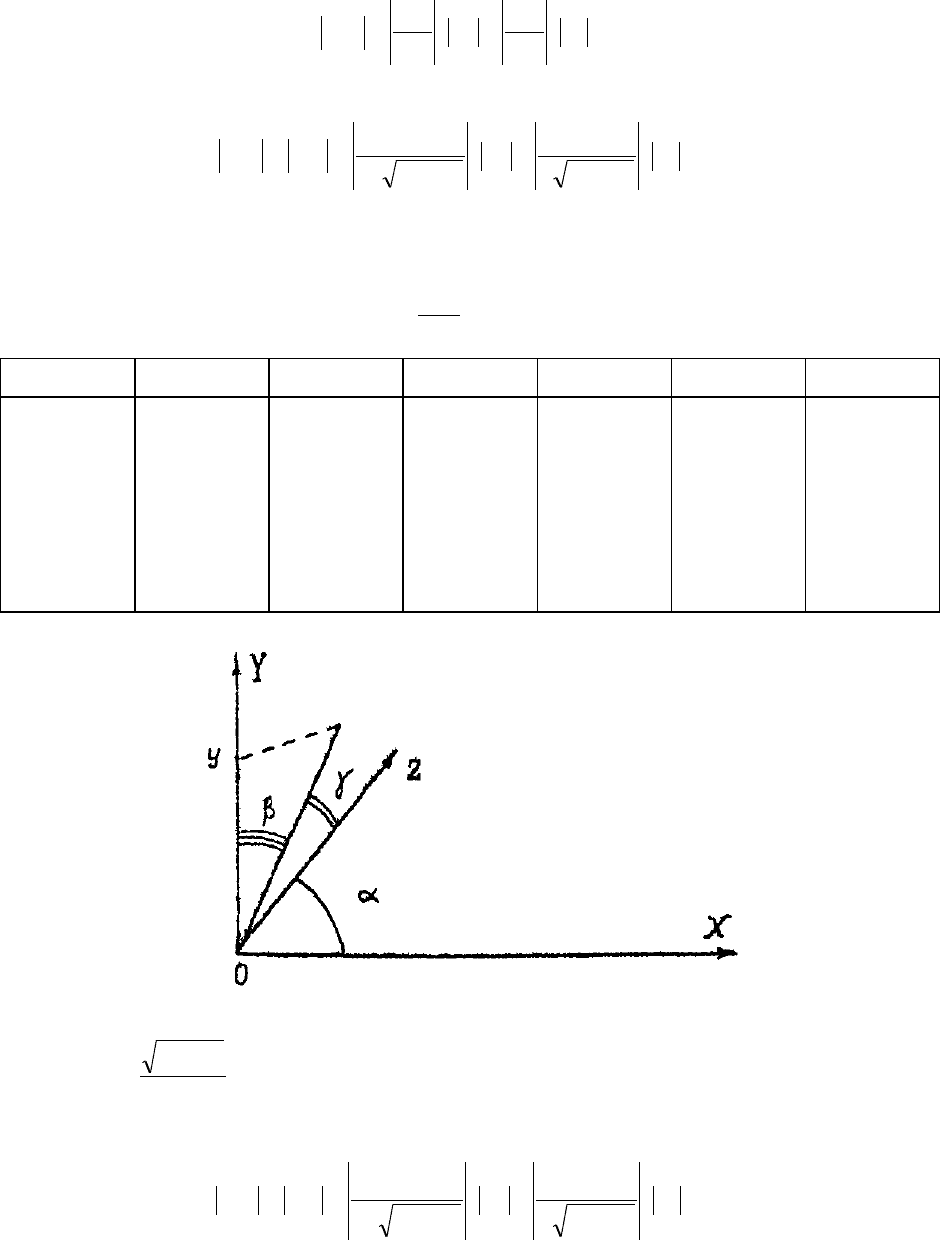
5
l
l
d
x
x
d
d
yy
y
. (3.2)
Из формулы (3.1) следует
l
lxx
l
x
lxx
l
kd
yy
22222
2
, (3.3)
где x = l = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
%100
y
y
d
d
. (3.4)
k
x
y, м
l, м
d
x
,м
d
xср
, м
d
x
,м
, %
1
0,005
1
1,2656*10
-4
1,2657*10
-4
1,27*10
-5
10,05
-1
-0,005
1,2656*10
-4
1,27*10
-5
10,05
2
0,01
1,2657*10
-4
6,39*10
-6
5,05
-2
-0,01
1,2657*10
-4
6,39*10
-6
5,05
3
0,015
1,2657*10
-4
4,28*10
-6
3,38
-3
-0,015
1,2657*10
-4
4,28*10
-6
3,38
Согласно рассуждениям из первой части опыта, аналогично получаем:
y
ly
kdd
xx
22
2
(3.5)
Из формул (3.2) и (3.5) получаем:
l
lyy
l
y
lyy
l
kd
xx
22222
2
, (3.6)
где y = l = 0,0005 м.
Для расчета относительной погрешности использовалась формула:
