Labelle P. Supersymmetry DeMYSTiFied
Подождите немного. Документ загружается.

This page intentionally left blank
CHAPTER 4
The Physics of
Weyl, Majorana,
and Dirac Spinors
In Chapter 2 we got acquainted with Weyl spinors and their behavior under Lorentz
transformations. However, as noted before, supersymmetric theories are often writ-
ten in terms of Majorana spinors instead. It is therefore important to understand
the connection among Weyl, Majorana, and Dirac spinors both at the mathematical
level and at the physical level. In addition, we will see how we can go back and
forth between Weyl and Majorana spinors. The first step is to understand the oper-
ation of charge conjugation applied to spinors and the connection with antiparticle
states.

68
Supersymmetry Demystified
4.1 Charge Conjugation and Antiparticles
for Dirac Spinors
Charge conjugation is the operation that turns a field describing a certain particle
into a field describing the corresponding antiparticle. To study the effect of charge
conjugation, let us consider a Dirac spinor because this probably is more familiar
to most readers. In this chapter and for the remainder of this book we will drop the
L and R labels on the Weyl spinors to alleviate the notation. It will be understood
that η will always represent a right-chiral spinor and χ a left-chiral spinor.
Consider, then, a Dirac spinor corresponding to a certain particle p (which could
be an electron, a neutrino, a quark, etc.):
p
=
η
p
χ
p
(4.1)
The antiparticle spinor is obtained by applying the charge-conjugation operator
(which we will write down explicitly in an instant) to the particle state, so we may
write
c
p
≡
¯
p
≡
η
¯
p
χ
¯
p
where the c denotes charge conjugation. Here, a bar over the name of a particle
simply will represent the corresponding antiparticle (as in ¯ν for the antineutrino).
It is unrelated to the bar used in Chapters 2 and 3.
Note that in a Dirac spinor, η
p
and η
¯
p
are two different right-chiral spinors.
The same comment applies to χ
p
and χ
¯
p
; they are different left-chiral spinors. But
clearly, those four spinors are related. To establish the connection, we need to work
out explicitly the charge conjugation.
The operation of charge conjugation is defined as
c
p
≡ C
T
p
(4.2)
where the bar denotes here the usual Dirac adjoint, and the charge-conjugation
matrix C may be taken to have the following representation:
C =−iγ
2
γ
0
=
iσ
2
0
0 −iσ
2

CHAPTER 4 The Physics of Spinors
69
With a little work, we may write Eq. (4.2) in a more convenient form:
c
p
= C
T
p
= C(
†
p
γ
0
)
T
= C(γ
0
)
T
†T
p
= Cγ
0
†T
p
≡ C
0
†T
p
where we have used (γ
0
)
T
= γ
0
and have introduced
C
0
= Cγ
0
=−iγ
2
γ
0
γ
0
=−iγ
2
=
0 iσ
2
−iσ
2
0
Here we have used the fact that γ
0
γ
0
= 1. Note that C
0
C
0
= 1 as well.
Written explicitly, the charge-conjugated state is
c
p
=
iσ
2
χ
†T
p
−iσ
2
η
†T
p
Using the fact that the charge-conjugated state is the antiparticle state, defined
in Eq. (4.1), we finally find
η
¯
p
= iσ
2
χ
†T
p
χ
¯
p
=−iσ
2
η
†T
p
(4.3)
This is an interesting result: These expressions are exactly what we obtained in
Eqs. (2.40) and (2.37)! What Eq. (4.3) tells us is that the right-chiral antiparticle
spinor is the right-chiral quantity built out of the particle left-chiral spinor! Like-
wise, the left-chiral antiparticle state is given by the left-chiral expression built out
of the right-chiral particle spinor. This is, by the way, the reason we introduced fac-
tors of i and −i in Eqs. (2.40) and (2.37): it was in order to make the correspondence
with charge conjugation exact.
It is easy to check that applying charge conjugation twice to a state gives back
the initial state:
(
c
p
)
c
= C
0
(
c
p
)
†T
= C
0
(C
0
†T
p
)
†T
= C
0
C
∗
0
p
= C
2
0
p
=
p
where we have used that the operation †T applied to a matrix (as opposed to a
quantum field) is simply a complex conjugation. Applying the charge conjugation
operation to both sides of Eq. (4.2), we find
p
= C
c
p
T
(4.4)
70
Supersymmetry Demystified
which leads to
η
p
= iσ
2
χ
†T
¯
p
χ
p
=−iσ
2
η
†T
¯
p
(4.5)
Of course, this also can be obtained directly by inverting Eq. (4.3).
As expected, the particle left-chiral spinor can be written as the left-chiral quan-
tity built out of the antiparticle right-chiral spinor. Likewise, the particle right-chiral
spinor can be written as the right-chiral expression built out of the antiparticle left-
chiral spinor.
Equations (4.3) and (4.5) teach us an important lesson: We are always free to
express the left- and right-chiral states of an antiparticle in terms of, respectively,
the right- and left-chiral states of the particle field (and vice versa). For example,
we may rewrite a Dirac spinor in terms of left-chiral fields only, at the condition of
introducing the left-chiral antiparticle state:
=
η
p
χ
p
=
iσ
2
χ
†T
¯
p
χ
p
(4.6)
This point will be crucial when we build the supersymmetric extension of the
standard model because we will express all fermions in terms of left-chiral states.
It must be kept in mind here that even though only left-chiral fields appear, the
upper two components still transform as a right-chiral spinor, so the four-component
spinor always has the structure:
=
quantity that transforms like a right-chiral spinor
quantity that transforms like a left-chiral spinor
Of course, we could as well have written the Dirac spinor in terms of right-chiral
fields only:
=
η
p
χ
p
=
η
p
−iσ
2
η
†T
¯
p
4.2 CPT Invariance
A short but crucial point needs to be mentioned here. Realistic relativistic quantum
field theories must be CPT-invariant (some authors write TCP or PCT); i.e., they
must be invariant under the combined operations of charge conjugation C, parity P,

CHAPTER 4 The Physics of Spinors
71
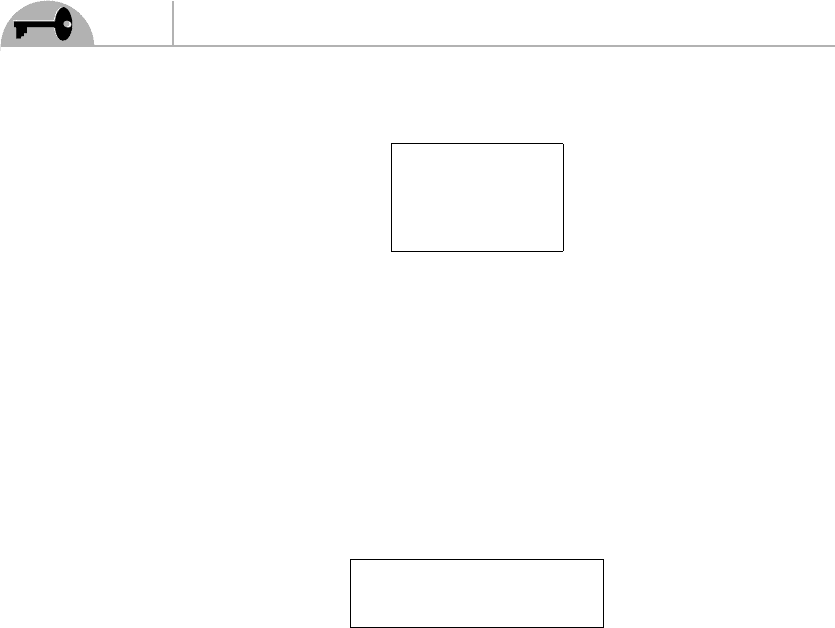
CPT
η
p
¯
χ
p
Figure 4.1 Two states related by CPT.
and time reversal T. A consequence of this requirement is that lagrangian densities
must be “real” in the sense that they must satisfy
L
†
= L (4.7)
This shows right away why we cannot have a theory containing a left-chiral
spinor χ without including as well its hermitian conjugate χ
†
because a lagrangian
containing only one of the two obviously could not respect Eq. (4.7).
Now, from Eq. (4.3) we see that χ
†
can be written in terms of the right-chiral
antiparticle spinor η
¯
p
. This means that the states χ
p
and η
¯
p
always appear together
in a CPT invariant field theory, which we illustrate in Figure 4.1.
In physical terms, this implies that if a theory contains a left-chiral spinor, it
also necessarily contains the corresponding antiparticle, which will be right-chiral.
When promoted to the status of quantum field operator, χ
p
creates the right-chiral
antiparticle and annihilates the left-chiral particle.
For similar reasons, the pair of fields shown in Figure 4.2 also must always
appear together in a CPT-invariant quantum field theory.
In other words, if there is a right-chiral particle state, there also must be a
corresponding left-chiral antiparticle state.
Actually, the two figures are totally equivalent because it is completely arbitrary
what we call the particle and what we call the antiparticle. So we are free to switch
the labels p and
¯
p in the first figure, which then becomes the second figure. What
we have learned is that if a particle of a certain chirality is present in a theory, there
will necessarily be a corresponding antiparticle of opposite chirality. If the particle
is massless, chirality and helicity can be used interchangeably.
Note that CPT invariance does not constrain us to necessarily have all four states
χ
p
,η
p
,χ
¯
p
, and η
¯
p
present. It is possible to build a completely consistent theory out
of χ
p
and η
¯
p
alone or out of χ
¯
p
and η
p
alone. We will discuss this key observation
more fully in the next few sections.
η
p
χ
¯p
CPT
Figure 4.2 Two other states related by CPT.

72
Supersymmetry Demystified
4.3 A Massless Weyl Spinor
Let us start with the simplest fermion theory that we could possibly imagine: the
theory of a noninteracting massless two-component Weyl spinor. We will take it to
be left-chiral. Then our lagrangian contains only the kinetic term given by
L
kin
= χ
†
¯σ
μ
i∂
μ
χ (4.8)
EXERCISE 4.1
Show that the lagrangian (4.8) is real in the sense of Eq. (4.7).
From what we learned in the preceding section, we know that one would observe
in the lab a left-chiral particle and its corresponding right-chiral antiparticle (again,
we could exchange the particle and antiparticle labels, but we choose to call the
left-chiral state the particle). It is instructive to make a count of the degrees of
freedom involved. A two-component spinor contains two complex variables, so
there are four “off-shell” degrees of freedom (i.e., four degrees of freedom before
the equations of motions are imposed). Physical massless spinors must obey the
Weyl equations Eq. (2.29), which provide two constraints, leaving two degrees of
freedom and therefore two types of observable states.
Since we know that the particles observed would be the left-chiral particle and the
corresponding right-chiral antiparticle, we should be able to write the lagrangian in
terms of χ
p
and η
¯
p
instead of χ
p
and χ
†
p
. Indeed, this can be done using the second
relation of Eq. (4.5):
χ
p
=−iσ
2
η
†T
¯
p
so that
χ
†
p
= η
T
¯
p
(−iσ
2
)
†
= η
T
¯
p
(iσ
2
)
The lagrangian then takes the form
L
kin
= η
T
¯
p
iσ
2
¯σ
μ
i∂
μ
χ
p
Note that this is a completely viable theory; there is no need to include the states
η
p
and χ
¯
p
. They are not needed to build a consistent theory. Of course, we could
choose to add them in, but then they would be totally independent and therefore
would correspond to a new particle in its own right.

CHAPTER 4 The Physics of Spinors
73
4.4 Adding a Mass: General Considerations
Let’s start again with a left-chiral Weyl spinor χ
p
, but now we will make it massive.
Before proceeding, it’s important to point out that some references restrict the
term Weyl spinors to massless spinors, in which case Weyl spinors are always
eigenstates of the helicity operator. Others define Weyl spinors as being the chirality
eigenstates, which are irreducible representations of the Lorentz group. With the
first definition, it is helicity that is used as the defining property of Weyl spinors,
whereas in the second convention, it is behavior under Lorentz transformations that
is judged as being more fundamental. For the proponents of the first definition,
massive Weyl fermions is an oxymoron, whereas the other camp has no problem
with that. Of course, in the massless case, the two schools of thought live in perfect
harmony; it is just when discussing massive particles that things get ugly.
In this book we will follow the second convention; i.e., we will use the term Weyl
spinors to denote the eigenstates of the chirality operator that have the Lorentz
transformations given in Eq. (2.32). Therefore, with our convention, it does make
sense to talk about massive Weyl spinors. The down side is that our massive Weyl
spinors do not have a well-defined helicity, but this is a small price to pay because
helicity will play very little role in this book.
Let’s get back to the physics of massive fermions. Things are much more in-
teresting than in the massless case. As we argued in Section 2.3, it is possible to
use a Lorentz transformation to change the helicity of a massive spinor. This im-
plies that we need both helicities to describe a general massive particle state. From
Eqs. (2.30) and (2.31) and the discussion preceding them, we must conclude that if
we need both helicity states to describe a massive particle, we need both chiralities
as well. Therefore, for a massive fermion, both chiralities of the particle must be
present in the theory.
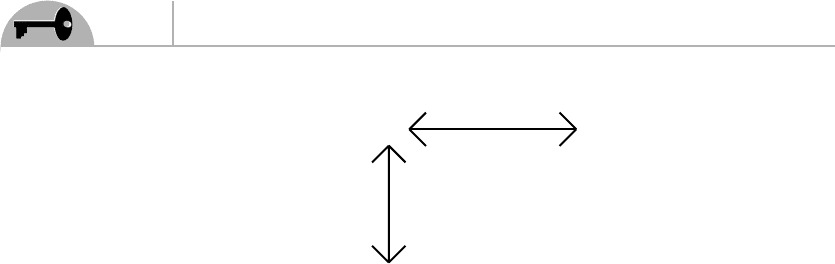
We can summarize the situation by saying that if we start with a left-chiral
particle state χ
p
, Lorentz transformations (LT) necessitate the introduction of a
right-chiral spinor η
p
, as illustrated schematically in Figure 4.3. This figure is not to
η
p
χ
p
LT
Figure 4.3 Two states of a massive spin 1/2 fermion required by Lorentz
transformations.
74
Supersymmetry Demystified
η
p
χ
p
LT
η
¯p
CPT
Figure 4.4 States associated to a massive left-chiral spinor through Lorentz and CPT
transformations.
be interpreted as saying that a Lorentz transformation changes a left-chiral state
into a right-chiral state—it is the helicity that is flipped by a Lorentz boost—but as
meaning that Lorentz transformations require the existence of both chiral states for
a massive fermion.
Now comes the interesting part. As we saw in the preceding section, CPT in-
variance forces us to introduce the charge-conjugate state η
¯
p
, which is right-chiral.
On the other hand, as we have just seen, for a massive particle, Lorentz invariance
also forces us to introduce a right-chiral state η
p
. The situation is summarized in
Figure 4.4.
The questions that come immediately to mind are: Can we take those two right-
chiral states forced on us to be the same? Can we take them to be different physical
states? In other words, do we have a choice?
The answer to all these questions is yes! We do have a choice, and this leads to
defining two different types of four-component spinors.
4.5 Adding a Mass: Dirac Spinors
First, let’s consider the case where we choose the two right-chiral states to represent
different physical states, η
p
= η
¯
p
. In that case, there are four physical (on-shell)
distinct states: the left- and right-chiral states of the particle χ
p
and η
p
as well as
the left- and right-chiral states of the antiparticle χ
¯
p
and η
¯
p
. This is illustrated in
Figure 4.5.
We can combine the left- and right-chiral states of the particle into a four-
component spinor that is the familiar Dirac spinor that we all know and love and
which we encountered in the first chapter:
D
=
η
p
χ
p
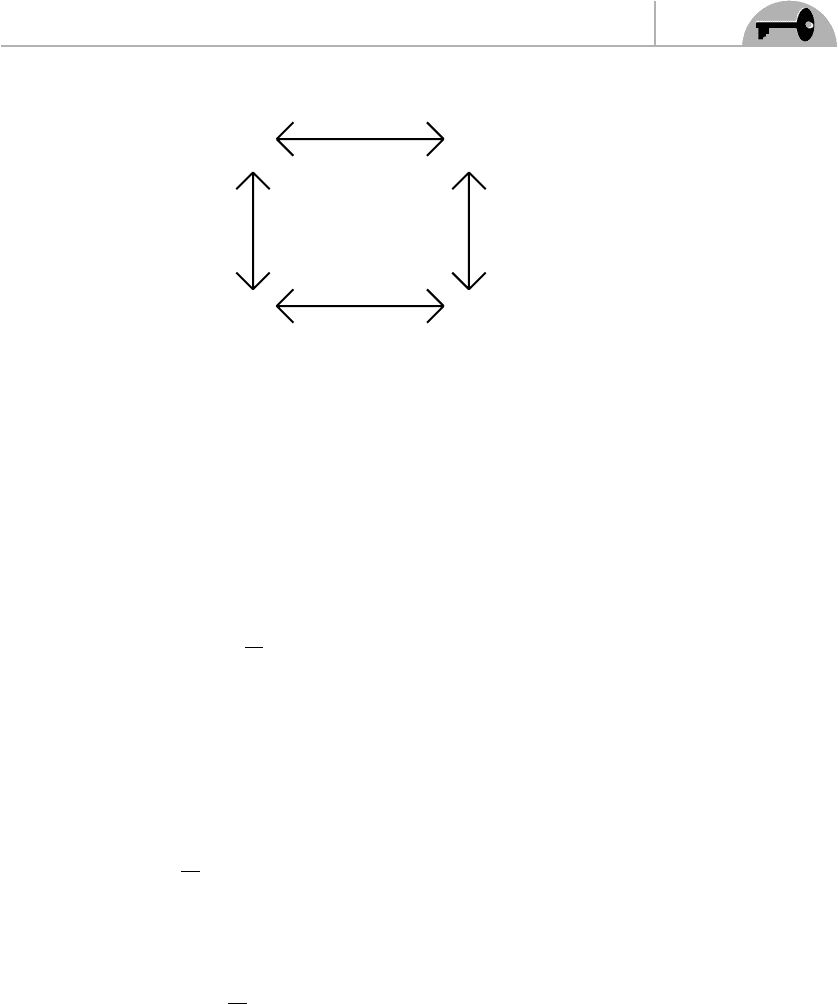
CHAPTER 4 The Physics of Spinors
75
η
p
χ
p
LT
η
¯p
CPT
CPT
LT
χ
¯p
Figure 4.5 The four states of a massive Dirac fermion.
Since we assume the antiparticle states χ
¯
p
and η
¯
p
to be distinct from χ
p
and η
p
,
we have
c
D
=
D
Let us write the mass term for such a Dirac spinor. From the Dirac lagrangian
Eq. (2.2), we know that the mass is
−m
D
D
=−m
†
γ
0
=−m
η
†
p
χ
p
+ χ
†
p
η
p
(4.9)
This shows clearly that both χ
p
and η
p
are necessary in order to write down a Dirac
mass term.
As noted earlier, we also could write the Dirac spinor in terms of left-chiral
spinors only, using Eq. (4.6). The mass term then is
−m
D
D
=−m
χ
T
¯
p
(−iσ
2
)χ
p
+ χ
†
p
iσ
2
χ
†T
¯
p
(4.10)
which, using the spinor dot products defined in Eq. (2.50), can be written in the
elegant form
−m
D
D
=−m(χ
¯
p
· χ
p
+ ¯χ
p
· ¯χ
¯
p
) (4.11)
EXERCISE 4.2
Show that the mass term in Eq. (4.11) is real in the sense of Eq. (4.7).
