Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

6.1. Сложность вычислений 201

Алгоритм 36. Симулятор работы машины Тьюринга

def executeMT (MT, input):

T ← MT["program"] # программа/таблица переходов

tape ← ["*"] + input # дописываем пробел слева от входа

state ← MT["start"] # начальное состояние

position ← 1 # положение головки

step ← 0 # счетчик тактов

while state 6= MT["stop"] ∧ step < 1000 :

step ← step + 1

if position ≥ len (tape): # потенциальная бесконечность

tape.append ("*") # ленты

symbol_under_head ← tap e[position]

action ← T [(state, (symbol_under_head))]

state ← action[0]

symbol_to_write ← action[1][0]

tape[position] ← symbol_to_write

move ← action[1][1]

if move = "L" : position ← position − 1

if move = "R" : position ← position + 1

3) «распознавание четных строк» (рис. 6.3);

4) «распознавание строки с одинаковым количеством 0 и 1»

(рис. 6.4 и 6.5).

Для каждой машины показано:

• табличное описание МТ;

• граф переходов;

• история выполнения для различных входных слов, где

для каждого такта выделено положение головки и указа-

но текущее состояние.

Упражнение 6.1.1. Постройте машину Тьюринга, которая

записывает входное двоичное слово в обратном порядке.

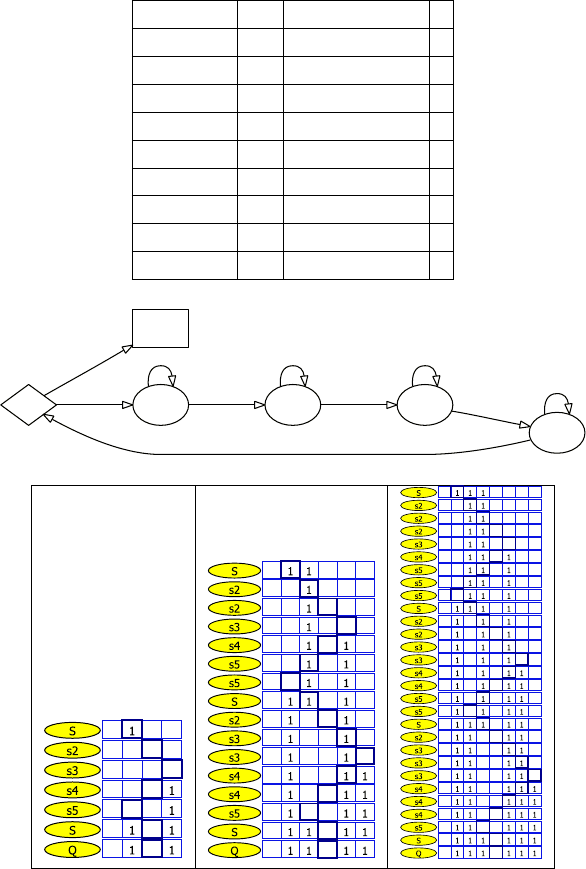
202 Глава 6. Основы теории сложности вычислений

<S> * ⇒ [Q] *

<S> 1 ⇒ s2 * R

s2 * ⇒ s3 * R

s2 1 ⇒ s2 1 R

s3 * ⇒ s4 1 L

s3 1 ⇒ s3 1 R

s4 * ⇒ s5 * L

s4 1 ⇒ s4 1 L

s5 * ⇒ <S> 1 R

s5 1 ⇒ s5 1 L

1L1

1R1

Рис. 6.1. Машина Тьюринга: удвоение строки

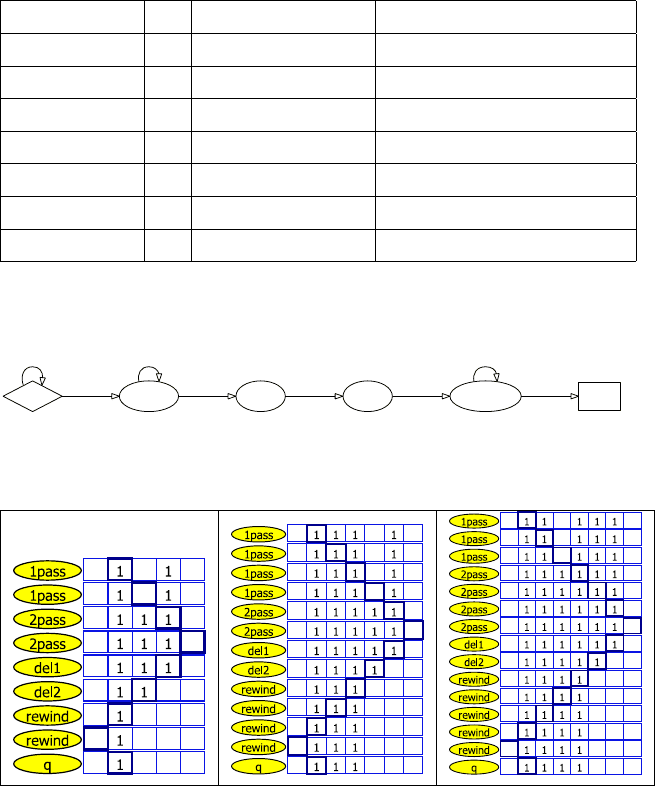
6.1. Сложность вычислений 203

<1pass> * ⇒ 2pass 1 R меняем разделитель

<1pass> 1 ⇒ <1pass> 1 R проходим первое число

2pass * ⇒ del1 * L конец второго числа

2pass 1 ⇒ 2pass 1 R проходим второе число

del1 1 ⇒ del2 * L удаляем 1-ю лишнюю 1

del2 1 ⇒ rewind * L удаляем 2-ю лишнюю 1

rewind * ⇒ [q] * R конец

rewind 1 ⇒ rewind 1 L перематываем к началу

1pass

2pass

qdel1 del2

rewind

1L1

Рис. 6.2. Машина Тьюринга: унарное сложение

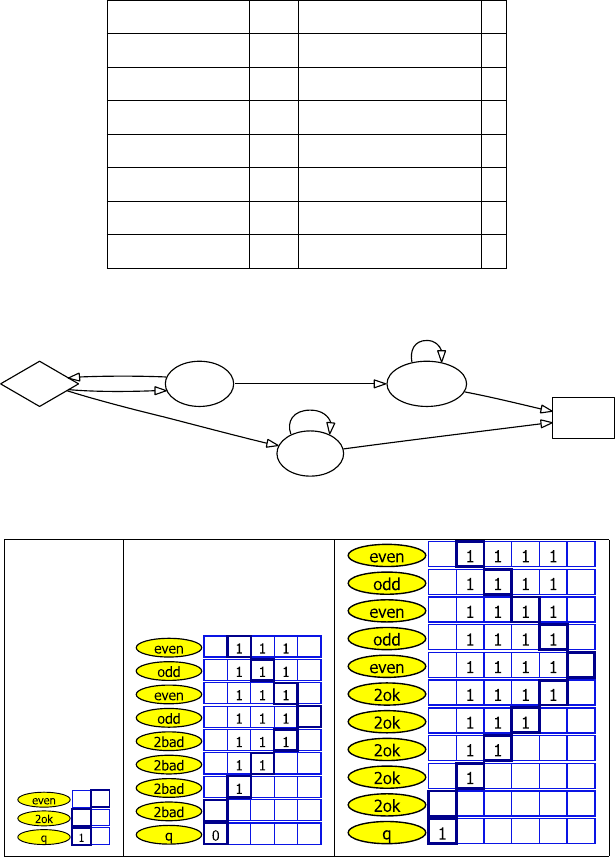
204 Глава 6. Основы теории сложности вычислений

2bad * ⇒ [q] 0

2bad 1 ⇒ 2bad * L

2ok * ⇒ [q] 1

2ok 1 ⇒ 2ok * L

<even> * ⇒ 2ok * L

<even> 1 ⇒ odd 1 R

odd * ⇒ 2bad * L

odd 1 ⇒ <even> 1 R

even odd

2ok

2bad

Рис. 6.3. Машина Тьюринга: распознавание четных строк

6.1. Сложность вычислений 205

2fail * ⇒ fail * R до начала

2fail . ⇒ 2fail * L проматываем в начало

2fail 0 ⇒ 2fail * L проматываем в начало

2fail 1 ⇒ 2fail * L проматываем в начало

2ok * ⇒ ok * R

2ok . ⇒ 2ok * L проматываем в начало

2start * ⇒ <s> * R становимся на первый символ

2start . ⇒ 2start . L

2start 0 ⇒ 2start 0 L проматываем все

2start 1 ⇒ 2start 1 L кроме маркера начала данных

fail * ⇒ [q] 0 R до начала

ok * ⇒ [q] 1 R пишем <1> и выходим

<s> * ⇒ 2ok * L не нашли 1 и 0 - все Ok

<s> . ⇒ <s> . R проматываем стертые символы

<s> 0 ⇒ skip0 . R стираем один ноль

<s> 1 ⇒ skip1 . R стираем одну единицу

skip0 * ⇒ 2fail * L не нашли симметричную единицу

skip0 . ⇒ skip0 . R проматываем стертые символы

skip0 0 ⇒ skip0 0 R проматываем 0-ли

skip0 1 ⇒ 2start . L стираем симметричную единицу

skip1 * ⇒ 2fail * L не нашли симметричный ноль

skip1 . ⇒ skip1 . R проматываем стертые символы

skip1 0 ⇒ 2start . L стираем симметричный ноль

skip1 1 ⇒ skip1 1 R проматываем 1-цы

skip0

2ok

skip1

2start

2fail

fail

0 .R

Рис. 6.4. Пример МТ: «Количество 0 и 1 равно?»

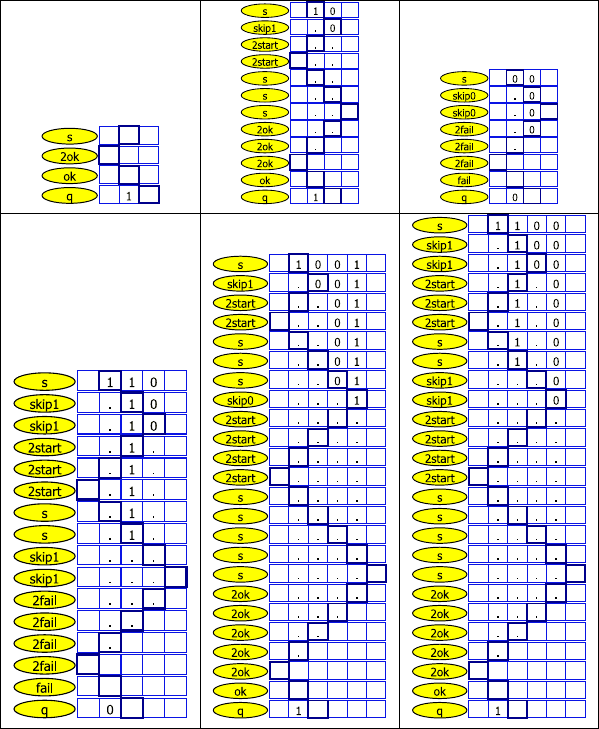
206 Глава 6. Основы теории сложности вычислений

Рис. 6.5. Выполнение МТ «Количество 0 и 1 равно?»

Упражнение 6.1.2. Постройте машину Тьюринга, которая

складывает два числа, записанные в двоичной системе. Для

определенности считайте, что записи чисел разделены специ-

альным символом алфавита «+».

6.1. Сложность вычислений 207

Заметим, что в различной литературе встречается доста-

точно большое число разновидностей определений МТ — на-

пример, число лент ограничивается до одной, бесконечной

только в одном направлении, или вводится «защита от за-

писи» на все ленты, за исключением выходной, разумеется,

и т. п.

Однако несложно, хотя и несколько утомительно, показать

эквивалентность всех этих определений в смысле вычислитель-

ной мощности. Мы тоже слегка затронем эту тему.

Для начала введем понятие универсальной машины Тью-

ринга, которая уже напоминает больше современный програм-

мируемый компьютер, чем механическую шкатулку.

Пусть T = hk+1, Σ, Γ

, α

, β

, γ

i и S = hk, Σ, Γ

, α

, β

, γ

k ≥ 1, две МТ, а p ∈ Σ

∗

. Итак, T с программой p симулирует

S, если для произвольного кортежа hx

, . . . , x

i ∈ Σ

∗

1) T останавливается на входе (x

, . . . , x

, p) тогда и только

тогда, когда S останавливается на (x

, . . . , x

);

2) в момент остановки T на первой ленте такое же содержи-

мое, как и на лентах S после остановки на том же входе.

Определение 6.1.2. k + 1 ленточная МТ T универсальна,

если для любой k-ленточной МТ S (над алфавитом Σ) суще-

ствует программа p ∈ Σ

∗

, на которой T симулирует S.

Теорема 6.1.1. Для любого k ≥ 1 и любого алфавита Σ суще-

ствует (k + 1) ленточная универсальная МТ.

Доказательство. Приведем конструктивное построение уни-

версальной МТ. Основная идея заключается в том, чтобы раз-

местить на дополнительной ленте универсальной МТ описание

и текущее состояние моделируемой машины S.

Для начала опишем построение с k+2 лентами. Для просто-

ты будем считать, что алфавит Σ содержит символы «0»,«1»

208 Глава 6. Основы теории сложности вычислений

и «−1». Пусть S = hk, Σ, Γ

, α

, β

, γ

i — произвольная k-

ленточная машина Тьюринга. Будем кодировать каждое со-

стояние машины S словом фиксированной длины r над алфа-

витом Σ

∗

. Тогда каждую строку из табличного представления

машины S можно записать строкой-кодом фиксированной дли-

ны:

. . . t

(g, t

, . . . , t

)β

(g, t

, . . . , t

)γ

(g, t

, . . . , t

g ∈ Γ; t

∈ Σ; ∀i = 1, . . . , k.

Итак, на «k + 1»-ой ленте у нас будет записано все таблич-

ное представление машины S в виде фиксированного размера

кодов, на «k + 2»-ой ленте изначально будет записано старто-

вое состояние S, на первых k лентах — входные данные.

Наша УМТ T будет пробегать по «k + 1»-ой ленте, пока те-

кущее состояние моделируемой машины S и символы t

. . . t

на лентах 1 . . . k не совпадут с записанным на «k + 2»-ой лен-

те кодом. Тогда из кода извлекаются инструкции, что делать

с первыми k лентами, новое состояние, которое записывается

на «k + 2»-ую ленту, и все повторяется.

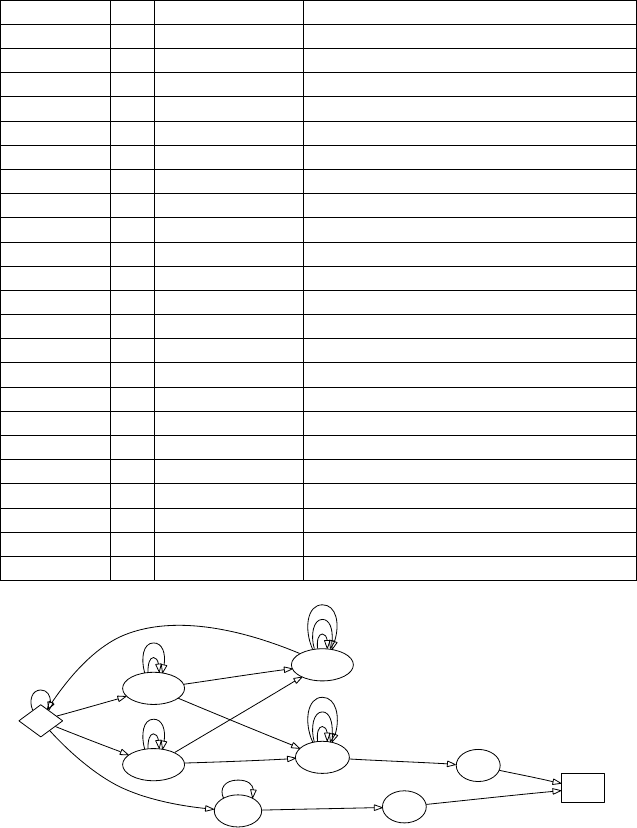
Для наглядности на рис. 6.6 приведен граф переходов

для 3-х ленточной УМТ, эмулирующей одноленточную МТ.

Большие прямоугольники обозначают состояния, вложенные

прямоугольники — условия переходов в другие состояния, на

ребрах-переходах прописаны совершаемые с лентами действия.

T (k), k = 1, 2, 3 — обозначают ленты, в контексте сравнения —

символ под головкой данной ленты.

Изначально машина находится в состоянии START, на

ленте T (3) записан код стартового состояния S. В состоянии

START мы пытаемся сравнить текущий код на ленте 2 и теку-

щее состояние S, записанное на ленте 3. Если они совпадают,

и совпадает с ожидаемым символ на первой ленте, то «перема-

тываем» к началу третью ленту (REWIND_T3), записываем

на нее новое состояние из второй ленты (WRITE_STATE),

6.1. Сложность вычислений 209

записываем на первую ленту символ из второй ленты, двигаем

куда надо головку первой ленты (MOVE), «перематываем»

к началу вторую и третью ленту (REWIND_T2_T3), и воз-

вращаемся в исходное состояние.

Иначе, по цепочке

SKIP_T2_STATE → SKIP_T2_TRANSITION → SKIP_T2_MOVE

(или более короткой) переходим к следующему коду (строке

моделируемой МТ) на второй ленте.

Переход от k + 2 лент к k + 1 несложен — например, доста-

точно хранить содержимое «k + 2»-й ленты в отрицательной

области «k + 1»-й ленты и моделировать 2 головки на «k + 1»-й

ленте (одна из которых будет работать с состоянием S, а другая

с программой S) методом, описанным в доказательстве следу-

ющей теоремы.

Следующая теорема утверждает, что в некотором смысле

неважно, сколько лент в определении МТ.

Теорема 6.1.2. Для любой k-ленточной МТ S существует

одноленточная МТ T, такая, что для любого x ∈ Σ

∗

, T оста-

навливается на x тогда и только тогда, когда на x останав-

ливается S, причем на ленте T после остановки записано то,

что записано после остановки на последней ленте S.

На входе x, на котором S будет работать N шагов, время

работы машины T будет O(N

Доказательство. Первым делом мы осуществляем «упаков-

ку» всех лент моделируемой машины S на одну ленту маши-

ны T. Мы добиваемся соответствия i-й ячейки j-й ленты мо-

делируемой машины S четной 2(ki + j − 1) ячейке единствен-

ной ленты машины T. Вернее, «упаковывается-растягивается»

только входная, первая лента машины S, т.к. остальные лен-

ты S по определению пусты перед запуском.

Позиции, соответствующие всем лентам S, кроме первой,

заполняются пробелами.

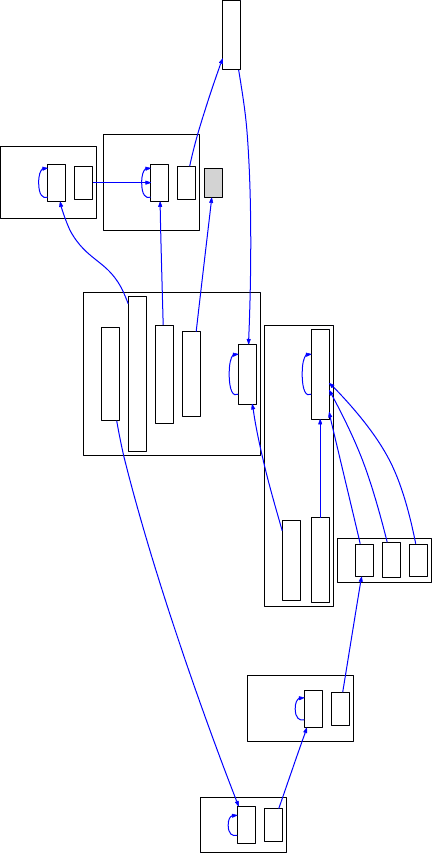
210 Глава 6. Основы теории сложности вычислений

START

SKIP_T2_STATE

SKIP_T2_TRANSITION

REWIND_T3

WRITE_STATE

MOVE

REWIND_T2_T3

T(1)=T(2) <>*

T(2).doRight

T(3).doRight

T(2)<>* AND T(3)<>* AND T(2)<> T(3)

T(3)<>*

T(2).doRight

T(3).doRight

T(3)=* AND T(2)<> T(1)

T(3)<>*

T(2).doRight

T(3).doLeft

T(3)=* AND T(2)= T(1)

T(3)<>*

T(2).doRight

T(3).doLeft

T(3)<>* AND T(2)=*

STOP

T(2).doRight

T(3).doRight

T(3)=*

T(2).doRight

T(3).doLeft

T(2).doRight

T(3).doLeft

T(3)=*

SKIP_T2_MOVE

T(2).doRight

T(3).doRight

T(3).doLeft

T(3)=*

T(3)<>*

T(3).doRight

T(3).write(T(2))

T(2).doRight

T(3).doRight

T(3)=*

T(2)=0

T(1).write(T(2))

T(2).doRight

T(3).doLeft

T(2)<>* AND T(3)<>*

T(2)=-1

T(1).doLeft

T(2)=1

T(1).doRight

T(2).doLeft

T(3).doLeft

T(2)<>* AND T(3)=*

T(2).doLeft

T(2)=* AND T(3)=*

T(2).doRight

T(3).doLeft

Рис. 6.6. Трехленточная универсальная МТ для одноленточных МТ