Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

4.4. Вероятностное округление 171

цессор принимает решение d

, остальные правильные процес-

соры должны иметь tally ≥ threshold, поскольку G ≥ H + t.

Следовательно, они все будут голосовать за одно и то же зна-

чение d

Теорема 4.3.8. Математическое ожидание числа раундов

для алгоритма ByzGen для достижения византийского со-

глашения ограничено константой.

4.4. Вероятностное округление

4.4.1. Вероятностное округление

для задачи «MAX-SAT»

Рассмотрим следующую задачу ([GW94]).

Задача 20. Максимальная выполнимость/MAX-SAT.

Даны m скобок конъюнктивной нормальной формы (КНФ)

с n переменными. Найти значения переменных, максимизи-

рующие число выполненных скобок.

В качестве примера рассмотрим следующую КНФ:

∨ x

)(x

∨ x

)(x

∨ x

)(x

∨ x

Переменные или их отрицания, входящие в скобку, называют-

ся литералами (так в первой скобке литералами являются x

и x

Задача MAX-SAT является N P-трудной, но мы рассмотрим

сейчас простое доказательство того, что для любых выполни-

мых m скобок существуют значения переменных, при которых

выполнено не менее m/2 скобок.

Теорема 4.4.1. Для любых m выполнимых скобок (т. е. ско-

бок, не содержащих одновременно переменную и ее отрица-

ние) существуют значения переменных, при которых выпол-

нено не менее m/2 скобок.

172 Глава 4. Вероятностные алгоритмы и их анализ

Доказательство. Предположим, что каждой переменной при-

писаны значения 0 или 1 независимо и равновероятно. Для

1 ≤ i ≤ m пусть Z

= 1, если i-я скобка выполнена, и Z

= 0

в противном случае.

Для каждой дизъюнкции (скобки) с k литералами (пере-

менными или их отрицаниями) вероятность, что эта дизъюнк-

ция не равна 1 при случайном приписывании значений пере-

менным, равна 2

−k

, поскольку это событие имеет место, когда

значение каждого литерала в дизъюнкции равно 0, а значе-

ния разным переменным приписываются независимо. Значит,

вероятность того, что скобка равна 1, есть 1 − 2

−k

≥ 1/2,

и математическое ожидание E Z

≥ 1/2. Отсюда математиче-

ское ожидание числа выполненных скобок (равных 1) равно

i=1

E Z

≥ m/2. Это означает, что есть приписы-

вание значений переменным, при котором

i=1

≥ m/2.

Эта теорема дает по существу приближенный вероятност-

ный алгоритм.

Определение 4.4.1. Вероятностный приближенный алго-

ритм A гарантирует точность C, если для всех входов I

1 ≥

E m

(I)

≥ C > 0,

где m

(I) — оптимум, m

(I) — значение, найденное алгорит-

мом, и решается задача максимизации.

Отличие приближенных алгоритмов от детерминирован-

ных состоит в рассмотрении математического ожидания вре-

мени работы.

Описанный в теореме 4.4.1 вероятностный алгоритм да-

ет точность 1/2 для MAX-SAT. Теперь опишем другой ве-

роятностный алгоритм, гарантирующий для MAX-SAT точ-

ность 3/4.

Для этого мы переформулируем MAX-SAT в задачу це-

лочисленного линейного программирования (ЦЛП). Каждой

4.4. Вероятностное округление 173

скобке (элементарной дизъюнкции) C

поставим в соответствие

булеву переменную z

∈ {0, 1}, которая равна 1, если скобка C

выполнена, каждой входной переменной x

сопоставляем пере-

менную y

, которая равна 1, если x

= 1, и равна 0 в противном

случае.

Обозначим C

индексы переменных в скобке C

, которые

входят в нее без отрицания, а через C

−

— множество индексов

переменных, которые входят в скобку с отрицанием.

Тогда MAX-SAT допускает следующую формулировку в ви-

де задачи ЦЛП:

j=1

→ max

i∈C

−

(1 − y

) ≥ z

∀j.

, z

∈ {0, 1} ∀i, j.

(4.1)

Упражнение 4.4.1. Докажите эквивалентность ЦЛП (4.1)

и задачи 20 «MAX-SAT».

Рассмотрим и решим линейную релаксацию целочисленной

программы (4.1).

j=1

→ max

i∈C

−

(1 − y

) ≥ z

∀j.

, z

∈ [0, 1] ∀i, j.

(4.2)

Пусть ^y

, ^z

— решение линейной релаксации (4.2). Ясно,

что

j=1

является верхней оценкой числа выполненных ско-

бок для данной КНФ.

174 Глава 4. Вероятностные алгоритмы и их анализ

Рассмотрим теперь вероятностный алгоритм 33 «вероят-

ностный MAX-SAT» (так называемое вероятностное округле-

ние), более интересный, чем тривиальное равновероятностное

округление каждой переменной в 1 и 0. При вероятностном

округлении в алгоритме 33 «вероятностный MAX-SAT» каж-

дая переменная y

независимо принимает значение 1 с вероят-

ностью ^y

(и 0 с вероятностью 1 − ^y

Алгоритм 33. Приближенный вероятностный алгоритм для

задачи 20 (MAX-SAT) на основе линейной релаксации

Вход: Формулировка задачи 20 «MAX-SAT» в виде (4.1)

^y ← решения линейной релаксации (4.2)

for all i ∈ {1..m} do

← 0

if random(0..1) ≤ ^y

then

← 1 {y

← 1 с вероятностью ^y

}

end if

end for

Выход: (y

, . . . , y

) — приближенное решение (4.1), со сред-

ней точностью (1 − 1/e).

Для целого k положим β

= 1 − (1 − 1/k)

Лемма 4.4.2. Пусть в скобке C

имеется k литералов.

Вероятность того, что она выполнена при вероятностном

округлении, не менее β

Доказательство. Поскольку мы рассматриваем отдельно взя-

тую скобку, без ограничения общности можно предположить,

что все переменные входят в нее без отрицаний (докажите этот

факт в качестве упражнения!). Пусть эта скобка имеет вид:

∨ . . . ∨ x

. Из ограничений линейной релаксации (4.2) сле-

дует, что

+ . . . + ^y

≥ ^z

4.4. Вероятностное округление 175

Скобка C

остается невыполненной при вероятностном округ-

лении, только если каждая из переменных y

округляется в 0.

Поскольку каждая переменная округляется независимо, это

происходит с вероятностью

i=1

(1 − ^y

). Остается только по-

казать, что

1 −

i=1

(1 − ^y

) ≥ β

Выражение в левой части достигает минимума при ^y

= ^z

для всех i. Остается показать, что 1−(1 −z/k)

≥ β

z для всех

положительных целых k и 0 ≤ z ≤ 1.

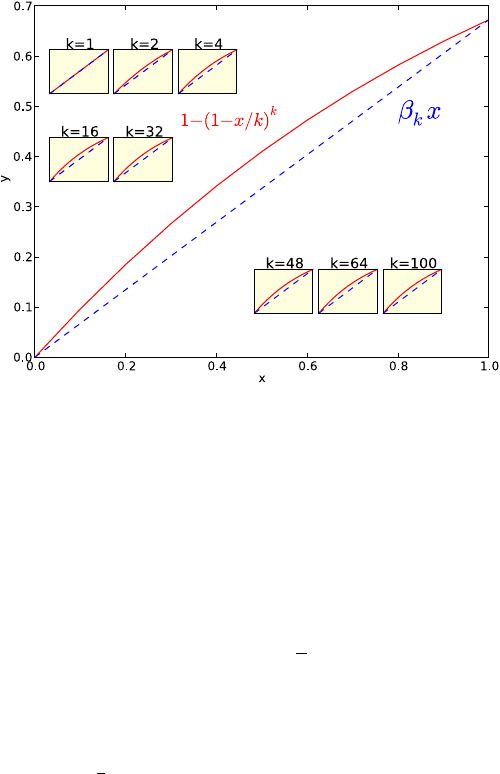
Поскольку f (x) = 1 − (1 − x/k)

— вогнутая функция (см.

рис. 4.4), для доказательства того, что она не меньше линейной

функции на отрезке, достаточно проверить это нестрогое нера-

венство на концах этого отрезка, т. е. в точках x = 0 и x = 1

(проделайте это в качестве упражнения).

Используя тот факт, что β

≥ 1 − 1/e для всех положитель-

ных целых k, получаем, что справедлива следующая

Теорема 4.4.3. Для произвольного входа задачи MAX-SAT

(произвольной КНФ) среднее число скобок, выполненных при

вероятностном округлении, не меньше (1 − 1/e) от макси-

мально возможного числа выполненных скобок.

А теперь мы опишем простую, но общую идею, которая поз-

волит получить приближенный вероятностный алгоритм, име-

ющий точность 3/4.

А идея такова: на данном входе запускаем два алгоритма

и выбираем из решений лучшее. В качестве двух алгоритмов

рассматриваем два алгоритма, описанных выше:

1) округление каждой переменной независимо в 0 или 1 с ве-

роятностью 1/2;

2) вероятностное округление решения линейной релакса-

ции соответствующей целочисленной программы (алго-

ритм 33 «вероятностный MAX-SAT»).

176 Глава 4. Вероятностные алгоритмы и их анализ

Рис. 4.4. График функции 1 − (1 − x/k)

при различных k

Для входной КНФ φ обозначим через n

= n

(φ) и

= n

(φ) число выполненных скобок для первого и второго

алгоритма соответственно.

Теорема 4.4.4.

E max{n

, n

} ≥

Доказательство. Поскольку для неотрицательных n

и n

вы-

полняется max{n

, n

} ≥ (n

+ n

)/2, достаточно показать, что

E(n

+ n

)/2 ≥

Пусть S

обозначает множество скобок, содержащих ровно

k литералов, тогда:

∈S

(1 − 2

−k

) ≥

∈S

(1 − 2

−k

)^z

4.4. Вероятностное округление 177

По лемме 4.4.2 имеем

E n

≥

∈S

Следовательно,

+ n

≥

∈S

(1 − 2

−k

) + β

Простое вычисление показывает, что (1 − 2

−k

) + β

≥ 3/2 для

всех натуральных k и, значит,

+ n

≥

∈S

4.4.2. Максимальный разрез в графе

Задачи полуопределенного и векторного про-

граммирования. Использование эффектив-

ных алгоритмов для решений этих задач

в вероятностном алгоритме решения зада-

чи о максимальном разрезе в графе. Раздел

основан на статье [GW95].

Определение 4.4.2. Матрица X ∈ R

n×n

является положи-

тельно полуопределенной если

∀a ∈ R

, a

Xa ≥ 0.

Обозначение: X < 0.

Для симметрической X ∈ R

n×n

следующее эквивалентно:

178 Глава 4. Вероятностные алгоритмы и их анализ

• X < 0;

• X имеет неотрицательные собственные значения;

• X = V

V для некоторого V ∈ R

m×n

, где m ≤ n.

Задача 21. «Полуопределенное программирование»

i,j

→ max(min)

∀k

i,j

ijk

= b

X = (x

) < 0,

∀i, j x

= x

Хотя задача 21 «SDP», несмотря на свою схожесть с линей-

ным программированием, к нему не сводится, для нее суще-

ствуют эффективные полиномиальные алгоритмы (модифика-

ции метода внутренней точки для ЛП), находящие приближен-

ное решение с некоторой аддитивной ошибкой  и временем,

ограниченным полиномом по длине входа и O(log(



)).

Заметим, что, так как решение задачи 21 «SDP» может

быть иррациональным числом, от численных методов точного

(рационального) решения ждать и невозможно, хотя продол-

жаются попытки построить эффективный алгоритм нахожде-

ния точного решения алгебраическими методами.

Далее нам также пригодится эквивалентная формулировка

задачи 21 «SDP» в виде задачи 22:

В англоязычной литературе SDP, semideﬁnite programming.

4.4. Вероятностное округление 179

Задача 22. «Векторное программирование»

i,j

· v

) → max(min)

∀k

i,j

ijk

· v

) = b

∀i v

∈ R

Эквивалентность задач 21 «SDP» и 22 «VP» следует из

факторизации положительно полуопределенной матрицы X

в виде X = V

V , т. е. x

= v

·v

, где v

и v

— соответствующие

колонки матрицы V .

Преобразование решения задачи 22 «VP» в решение зада-

чи 21 «SDP» тривиально (одно матричное умножение), обрат-

ное не совсем — требуется разложение Холецкого

, и это пре-

образование неоднозначно, но ничего принципиально сложного

в этом нет — это классическая задача линейной алгебры.

Вероятностное округление при нахождении аппрокси-

мации максимального разреза

Определение 4.4.3. Пусть есть неориентированный граф

G = (V, E). Разрезом (сечением, cut) называется разбие-

ние множества вершин V на непересекающиеся множества

S и T . т. е. V = S ∪ T и S ∩ T = ∅.

Определение 4.4.4. Для неориентированного графа G = (V, E)

и разреза (S, T ) ребро e = (v, t) считается пересекающим

разрез, если v ∈ S, а t ∈ T .

Определение 4.4.5. Для графа G = (V, E) размером разреза

(S, T ) считается число ребер, пересекающих этот разрез.

В англоязычной литературе VP, vector programming.

Cholesky factorization или Cholesky decomposition.

180 Глава 4. Вероятностные алгоритмы и их анализ

Если граф — взвешенный, т. е. каждому ребру e ∈ E со-

ответствует некоторый вес w

, то размером разреза (S, T )

считается сумма весов ребер пересекающих этот разрез:

R(S, T ) =

e=(v,t)∈E: v∈S,t∈T

Задача 23. «Максимальный разрез/MAX-CUT».

Для взвешенного неориентированного графа G = (V, E)

с весами w

> 0 найти разрез (S, T ) с максимальным весом

R(S, T ).

Упражнение 4.4.2. Докажите, что для простого, невзвешен-

ного графа в задаче 23 «MAX-CUT» можно применить про-

стую стратегию, дающую вероятностный 0.5-приближенный

алгоритм: для каждой вершины с вероятностью 1/2 отнести

ее к множеству S и с вероятностью 1/2 — к множеству T .

Упражнение 4.4.3. Студент предлагает для задачи 23 «MAX-

CUT» приближенный алгоритм с точностью

: положить

первую вершину в одну часть, последнюю — в другую, за-

тем по-очереди добавлять оставшиеся вершины, к множеству,

с которым у этой вершины меньше ребер-связей.

Прав ли студент?

Наша цель — построить алгоритм с лучшими оценка-

ми точности приближения. Для этого сформулируем зада-

чу 23 «MAX-CUT» как задачу целочисленного программиро-

вания.

Задача 24. «MAX-CUT(ЦП)»

G = (V, E) — входной граф, |V | = n;

W = (w

) — веса ребер, n×n матрица. Для отсутствующего

между v

и v

ребра — w

= 0;