Кузюрин Н.Н. Фомин С.А. Эффективные алгоритмы и сложность вычислений

Подождите немного. Документ загружается.

5.1. Метод условных вероятностей 191

Из теоремы 4.4.3 следует, что E X ≤ (1/e)m, а из (5.3) вы-

текает, что X(x

= d

, . . . , x

= d

) ≤ (1/e)m.

Таким образом, мы находим допустимый 0–1 вектор

x = (x

, . . . , x

) с гарантированной верхней оценкой для целе-

вой функции.

Важный вопрос заключается в том, как эффективно вычис-

лять условные математические ожидания. Предположим, зна-

чения первых k переменных уже определены и I

— множество

индексов переменных, значения которых равны 0, а I

— мно-

жество индексов переменных, значения которых равны 1.

Нетрудно проверить, что если I

∩ C

−

6= ∅ или I

∩ C

6= ∅,

то P

= 0. В противном случае

i∈C

(1 − p

) ·

i∈C

−

. (5.4)

Запишем этот алгоритм более формально, в виде алгорит-

ма 35 «MAX-SAT дерандомизация».

Упражнение 5.1.1. Покажите, что можно организовать

вычисление f

и f

таким образом, что сложность алгорит-

ма 35 «MAX-SAT дерандомизация» (кроме решения линейной

релаксации) будет O(mn).

Упражнение 5.1.2. Честный попутчик в поезде предлагает

вам сыграть в следующую игру, вариант классического «на-

перстка». т. е. есть три наперстка, шарик, ваша задача обна-

ружить шарик — тогда вы выигрываете, иначе — выигрывает

сдающий.

Каждый раз на кон, вы и сдающий, ставите по 50 рублей.

Сдающий тасует три наперстка, и прячет под одним из них ша-

рик. Затем он предлагает вам выбрать наперсток. После того,

как вы выбрали наперсток (пусть это будет наперсток «A»),

вы можете открыть его, либо, заплатив еще 10 рублей, потре-

бовать от сдающего, открыть пустой наперсток из двух остав-

192 Глава 5. Методы дерандомизации

шихся (пусть открытый будет «B»), после чего выбрать один

из двух закрытых наперстков (т. е. «A» или «С»).

Заметим, что сдающий и предметы честные (никаких «ис-

чезающих» шариков и прочего мошенничества, наперсток для

шарика выбирается совершенно случайно).

Какая стратегия оптимальна?

1) Не играть. Выигрыш — 0.

2) Выбрать наперсток «A» и открыть его.

3) Выбрать наперсток «A», «купить» открытие пустого на-

перстка «B», но выбрать наперсток «A».

4) Выбрать наперсток «A», «купить» открытие пустого на-

перстка «B», и выбрать наперсток «С».

Дорога длинная, играть можно много раз, правильная

стратегия может привести к существенному обогащению,

неправильная — к разорению. . .

Обоснуйте. Подсчитайте матожидание выигрыша для каж-

дой из стратегий.

Рис. 5.2. Карта-памятка раздела 5.1.0

5.2. Метод малых вероятностных пространств 193

5.2. Метод малых вероятностных

пространств

В разделе 4.3.1 мы уже рассматривали параллельный веро-

ятностный алгоритм Parallel MIS, для поиска максималь-

ного по включению независимого множества (см. определе-

ние 4.3.2 «MAX-IND-SET»), причем у этого алгоритма средним

числом итераций было логарифмическим от длины входа.

Идея дерандомизации этого алгоритма заключается в том,

чтобы показать, что вероятностный анализ работает аналогич-

ным образом, даже если пометки вершин делаются не полно-

стью независимо, а попарно независимо. Отметим, единствен-

ное место в анализе алгоритма, где использовалась независи-

мость пометок, была лемма 4.3.2.

Справедлива следующая

Лемма 5.2.1. Если в алгоритме Parallel MIS случайные

пометки вершин делаются попарно независимо, то вероят-

ность того, что хорошая вершина принадлежит множеству

S ∪ Γ(S), не меньше, чем 1/24.

Ключевое преимущество попарной независимости состоит

в том, что только O(log n) случайных бит достаточно для по-

рождения всех точек соответствующего вероятностного про-

странства.

Число точек в таком пространстве есть O(n

) и может быть

просмотрено полным перебором за полиномиальное время.

Доказательство леммы. Единственное место, где исполь-

зовалась полная независимость пометок вершин, была нижняя

оценка вероятности, что хорошая вершина становится помечен-

ной. Была использована следующая оценка.

Пусть X

, 1 ≤ i ≤ n — {0, 1}–случайные величины

и p

= P(X

= 1). Если X

независимы в совокупности, то

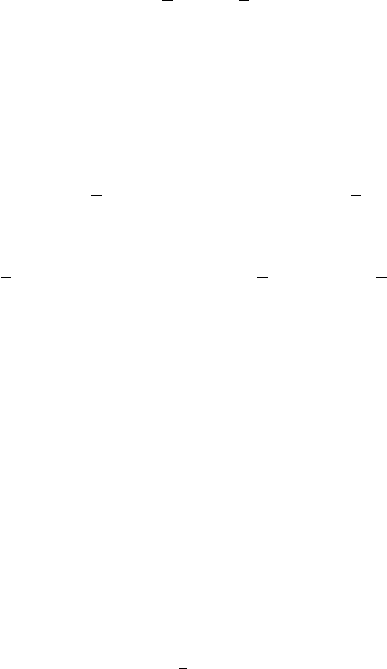
194 Глава 5. Методы дерандомизации

> 0

≥ 1 −

(1 − p

Мы заменим эту оценку соответствующей оценкой для по-

парно независимых случайных величин.

Утверждение. Пусть X

, 1 ≤ i ≤ n — {0, 1}–случайные

величины и p

= P(X

= 1). Если X

попарно независимы, то

> 0

≥

min

(

)

Доказательство. Предположим, что

≤ 1/2.

Обозначим через Y

событие X

= 1. Имеем по формуле

включений-исключений:

P(∪

) ≥

P(Y

) −

i,j

P(Y

∧ Y

) =

−

i,j

−

≥

1 −

≥

Если

> 1/2, то ограничим индексы суммирования по

подмножеству S ⊆ [n], такому, что 1/2 ≤

≤ 1, и повторим

то же доказательство.

Завершим теперь доказательство леммы.

Напомним, что вершина v ∈ V называется хорошей, если

она имеет не менее d(v)/3 соседних вершин степени не более

d(v). В противном случае вершина называется плохой.

Покажем, что если v — хорошая вершина, то вероятность

того, что найдется помеченная вершина из Γ(v), не меньше

1/12.

Обозначим эту вероятность через P(Γ(v)

marked

Обозначим Γ

∗

(v) = {w ∈ Γ(v)| d(w) ≤ d(v)}. По определе-

нию хорошей вершины |Γ

∗

(v)| ≥

d(v). Используя доказанную

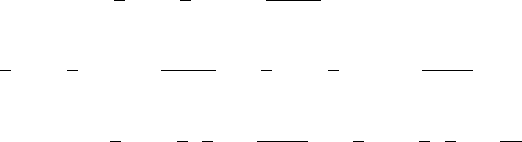
5.2. Метод малых вероятностных пространств 195

выше оценку для попарно независимых случайных величин,

имеем

P(Γ(v)

marked

) ≥

min{

w∈Γ(v)

2d(w)

} ≥

≥

min{

w∈Γ

∗

(v)

2d(w)

} ≥

min{

w∈Γ

∗

(v)

2d(v)

} ≥

≥

min{

d(v)

2d(v)

} ≥

min{

} =

Используя лемму 4.3.3 из анализа вероятностного алгорит-

ма Луби (В течение каждой итерации, если вершина поме-

чена, то она выбирается в S с вероятностью не менее 1/2)

и учитывая тот факт, что в ее доказательстве использовалась

только попарная независимость, получаем доказательство на-

шей леммы.

Попарная независимость для неодинаково

распределенных случайных величин. Конструкция

Покажем теперь, как осуществить дерандомизацию путем пол-

ного перебора элементарных событий (точек) из вероятност-

ного пространства и вычисления в каждой точке этого про-

странства. Элементарным событием будет приписывание по-

меток вершинам графа, задаваемое булевым вектором длины

n. Размер построенного пространства будет полиномиальным.

Для дерандомизации путем полного перебора точек из постро-

енного вероятностного пространства достаточно будет вычис-

лить в каждой точке подмножество вершин R, соответствую-

щее шагу 2.1 алгоритма Parallel MIS, затем для каждого ребра

в R выбросить концевую вершину меньшей степени (шаг 2.2

алгоритма), подсчитать число N

ребер, смежных с оставшим-

ся множеством вершин. Затем взять множество R, максимизи-

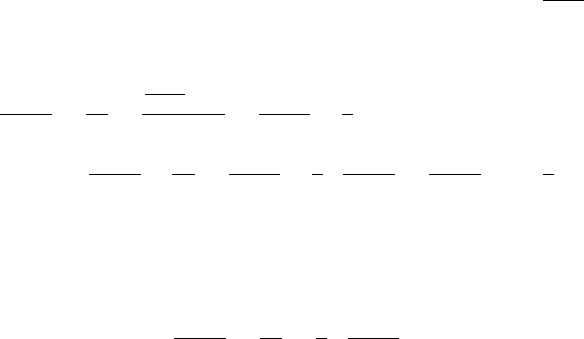
196 Глава 5. Методы дерандомизации

рующее показатель N

. Оно обеспечит требуемые оценки на

число итераций детерминированного алгоритма.

Итак, для осуществления указанного метода дерандомиза-

ции нужна конструкция небольшого вероятностного простран-

ства со свойством попарной независимости соответствующих

случайных величин. Опишем эту конструкцию.

Выберем наименьшее простое число p, такое, что cn ≤ p, где

точное значение константы c > 1 выберем далее. Для каждой

вершины u выберем целое a

, такое, что a

/p ≈ 1/2d(u) и ин-

тервал A

, |A

| = a

в Z

. Более точно, положим a

= d

2d(u)

Тогда

2d(u)

≤

2d(u)

+ 1

2d(u)

≤

2d(u)

≤

2d(u)



1 +



Достаточно выбрать c = 10, чтобы для вероятности вершины u

быть помеченной на шаге 2.1 алгоритма Parallel MIS было вы-

полнено неравенство

2d(u)

≤

2d(u)

Упражнение 5.2.1. Покажите, что при указанном выборе

вероятностей пометки вершин анализ алгоритма Parallel MIS,

проведенный в разделе 4.3.1, остается в силе с небольшим изме-

нением констант. В частности, лемма 4.3.2 справедлива без из-

менений, в лемме 4.3.3 оцениваемая вероятность не меньше 2/5,

в лемме 4.3.4 — соответственно не менее (2/5) · (1 − e

−1/6

Упражнение 5.2.2. Покажите, что при указанном выборе

вероятностей пометки вершин анализ алгоритма Parallel MIS,

проведенный в данном разделе выше, остается в силе с неболь-

шим изменением констант. В частности, лемма 4.3.2 справед-

лива без изменений, в лемме 4.3.3 оцениваемая вероятность не

5.2. Метод малых вероятностных пространств 197

меньше 2/5, в лемме в данном разделе — соответственно не

менее (2/5) · (1/12) =

Пусть X(u) — случайная величина, полученная путем рав-

номерного выбора x, y ∈ Z

следующим образом: X(u) = 1,

если xu + y ∈ A

, и нулю в противном случае.

Это значит, что P(X(u) = 1) = a

/p, поскольку

x,y

(X(u) = 1) = P(∃a ∈ A

: xu + y = a) =

a∈A

P(x = (a − y)u

−1

) =

a∈A

Для доказательства попарной независимости достаточно

показать, что

P(X(u) = 1, X(v) = 1) = P(X(u) = 1) P(X(v) = 1) =

Имеем

P(X(u) = 1, X(v) = 1) =

= P(∃a ∈ A

, b ∈ A

: xu + y = a, xv + y = b) =

a∈A

, b∈A

P(xu + y = a, xv + y = b) =

a∈A

, b∈A

Глава 6

Основы теории сложности

вычислений

При написании этой главы использовались курсы лекций

[Lov99], [Gol99], а также отчет [96] и книга [99b].

6.1. Сложность вычислений

6.1.1. Машины Тьюринга и вычислимость

Неформально, машина Тьюринга (далее МТ) представляет со-

бой автомат с конечным числом состояний и неограниченной

памятью, представленной набором одной или более лент, бес-

конечных в обоих направлениях. Ленты поделены на бесконеч-

ное число ячеек, и на каждой ленте выделена стартовая ячейка.

В каждой ячейке может быть записан только один символ из

некоторого конечного алфавита Σ, где предусмотрен символ ?

для обозначения пустой ячейки.

На каждой ленте имеется головка чтения-записи, и все они

подсоединены к «управляющему модулю» МТ — автомату с ко-

нечным множеством состояний Γ. Имеется выделенное стар-

товое состояние «START» и состояние завершения «STOP».

Перед запуском МТ находится в состоянии «START», а все го-

ловки позиционированы на нулевые ячейки соответствующих

6.1. Сложность вычислений 199

лент. На каждом шаге все головки считывают информацию из

своих текущих ячеек и посылают ее управляющему модулю

МТ. В зависимости от этих символов и собственного состояния

управляющий модуль производит следующие операции:

1) посылает каждой головке символ для записи в текущую

ячейку каждой ленты;

2) посылает каждой головке одну из команд «LEFT»,

«RIGHT», «STAY»;

3) выполняет переход в новое состояние (которое, впрочем,

может совпадать с предыдущим).

Теперь то же самое более формально.

Определение 6.1.1. Машина Тьюринга — это набор

T = hk, Σ, Γ, α, β, γi, где

• k ≥ 1 — число лент;

• Σ — алфавит лент, ? ∈ Σ — символ-пробел;

• Γ — конечное множество состояний, S, Q ∈ Γ — выде-

ленные состояния: запуск машины и завершение работы;

• α, β, γ — произвольные отображения:

α : Γ × Σ

→ Γ,

β : Γ × Σ

→ Σ

γ : Γ × Σ

→ {−1, 0, 1}

т. е. α задает новое состояние, β — символы для записи

на ленты, γ — перемещение головок. Таким образом, маши-

на Тьюринга задается таблицей команд размером |Σ|

× |Γ|,

200 Глава 6. Основы теории сложности вычислений

задающей правила работы машины в соответствии с функци-

ями α, β, γ. Удобно считать, что алфавит Σ содержит кроме

«пробела» ? два выделенных символа — 0 и 1

Под входом для МТ подразумевается набор из k слов (k-

кортеж) из Σ

∗

, записанных справа от стартовых позиций на

k лентах МТ. Обычно входные данные записывают только

на первую ленту, и под входом x подразумевают k-кортеж

hx, ∅, . . . , ∅i — так мы и будем считать дальше в этом разделе.

Результатом работы МТ на некотором входе X считает-

ся слово, записанное на последней ленте после остановки МТ

(слова, записанные на остальных лентах, принято игнориро-

вать).

Алфавит входного слова будем обозначать Σ

= Σ\{?}. Да,

мы будем считать без потери общности, что входное слово не

содержит пробелов ? — иначе возникнут технические сложно-

сти, как определить, где кончается входное слово и т. п.

Если что-то осталось непонятным, можно посмотреть на ал-

горитм 36 «Симулятор MT» — симулятор работы МТ, который

мы будем использовать, чтобы проиллюстрировать процесс ра-

боты машин Тьюринга. Он принимает на вход описание маши-

ны Тьюринга в виде таблицы команд (см. рис. 6.1).

Обратите также внимание на альтернативное представле-

ние машин Тьюринга в виде ориентированных графов, где вер-

шины являются состояниями, а дуги — возможными сменами

состояний, причем начало дуги помечено символом, который

должен быть на ленте для активации перехода, а конец дуги

помечен символом, который пишется на ленту, и командой пе-

ремещения головки: «L» (влево), «R» (вправо), «» (на месте).

Рассмотрим несколько примеров машин Тьюринга:

1) «удвоение строки» (рис. 6.1);

2) «унарное сложение» (рис. 6.2);

Обычно вовсе ограничиваются алфавитом Σ ≡ {?, 0, 1}.