Кузнецов О.Л., Никитин А.А., Черемисина Е.Н. Геоинформатика и геоинформационные системы

Подождите немного. Документ загружается.

ГРИД. В России для этой цели образован консорциум РДИГ (Российский

ГРИД для интенсивных операций с данными – Russian Data Intensive GRID

или RGRID).

Консорциум РДИГ входит в проект в качестве региональной федера-

ции «Россия» наравне с ЦЕРН (Европейской лабораторией по физике час-

тиц), выполняющей координирующие функции по проекту, и другими

восьмью национальными и региональными федерациями (Франция, Италия,

Великобритания/Ирландия, Германия/Швейцария, Скандинавские страны,

консорциумы Центрально-Европейских стран, Юго-восточной Европы и

Юго-западной Европы).

В консорциум РДИГ входят такие организации, как ИФВЭ (институт

физики высоких энергий, Протвино), ИМПБ (институт математических

проблем биологии, Пущино), ИТЭФ (институт теоретической и эксперимен-

тальной физики), ОИЯИ (Объединенный институт ядерных исследований,

Дубна), ИПМ (институт прикладной математики, г. Москва), ПИЯФ (Петер-

бургский институт ядерной физики, Гатчина), ИАЭ (институт атомной энер-

гии), НИИЯФ МГУ (научно-исследовательский институт ядерной физики

МГУ).

Основными нерешенными проблемами в развитии проекта EGEE яв-

ляются: отсутствие национальной программы ГРИД-технологий; отсутствие

подготовки специалистов в области ГРИД-технологий и отсутствие реаль-

ной действующей ГРИД-инфраструктуры, способствующей распростране-

нию новых технологий для различных технических приложений.

Вопрсы для самоконтроля.

1. Что такое вычислительная сеть?

2. Сформулируцйте основные характеристики локальной вычис-

лительной сети.

3. Основные типы топологий локальной сети, их преимуществаи

недостатки.

4. Охарактеризуйте типы линий связи.

5. Структура пакета в протоколе HDLC.

6.Основные уровни и их функции эталонной модели взаимодейст-

вия открытых систем.

7. Привидите примеры локальных вычислительных сетей.

ГЛАВА X. ИНТЕГРИРОВАННЫЙ СИСТЕМНЫЙ АНАЛИЗ

ГЕОИНФОРМАЦИИ

В последние десятилетия в исследовании геологических объектов и

глубинного строения земной коры одним из быстроразвивающихся направ-

лений является интегрированный системный анализ геоинформации.

Это направление отражает происходящие в геологии и геофизике ка-

чественные изменения, связанные с:

– резким увеличением объемов регистрируемой информации, как за

счет повышения плотности наблюдений (3D и 4D сейсморазведки,

пространственно временные измерения при электромагнитных зон-

дированиях и т.д.) и разнообразия методов исследований, так и за

счет их многоуровневого характера: от скважинных наблюдений до

космоса;

– развитием теории и средств описания протекающих в земной коре

процессов и их отражения в геофизических и геохимических полях

разного уровня;

– оснащением геолого-геофизических организаций мощными компью-

терными системами и персональными ЭВМ, обеспечивающими ак-

тивное включение интерпретатора в процесс решения трудноформа-

лизуемых задач по изучению недр.

Комплексный и многоуровневый характер геоинформации обуслав-

ливает необходимость использования системного анализа при обработке и

интерпретации данных.

В настоящем разделе рассматриваются основные принципы и кон-

кретные методы интегрированного системного анализа геоинформации, на-

правленные на решение типичных задач прикладной геофизики: обнаруже-

ния и локализации перспективных объектов, их распознавания и классифи-

кации, построения многофакторных моделей геообъектов и геосреды.

10.1. Понятие и принципы интегрированного системного

анализа геоинформации

Регистрация геофизических, геологических и геохимических полей

на разных уровнях наблюдений: космические (спутниковые), повысотные

(аэросъемка на нескольких высотах), наземные, подземные и скважинные

измерения – существенным образом расширяют информацию об изучаемых

геообъектах и геопроцессах, а также возможности ее обработки и интерпре-

тации на ЭВМ с целью решения различных задач недро- и природопользо-

вания.

При этом становится актуальной проблема создания методологии

(общих принципов) и конкретных методов комплексирования разнородной

(разнометодной) и многоуровневой геоинформации. Методология и методы

комплексной обработки и интерпретации разнородной и многоуровневой

информации могут быть созданы лишь на основе системного анализа такой

сложной информации, какой является геоинформация.

Системный анализ – это совокупность методов, ориентированных

на проблемы принятия решений в условиях, когда выбор альтернативы тре-

бует изучения сложной информации разной природы [24].

Методология системного анализа основана на методах исследования

операций, теории принятия статистических решений и управления. В при-

кладной геофизике целью комплексной обработки и интерпретации разно-

родной и многоуровневой информации является создание объемных много-

факторных физико-геологических моделей, т.е. системы объектов разного

уровня, и принятия управленческих решений о направлении дальнейших

исследований: бурить ли скважины или прекратить изучение района ввиду

его неперспективности или продолжать изучение другими методами из-за

недостаточности информации об объектах исследований.

При анализе геоинформации с четырех уровней зондирования лито-

сферы следует учитывать разновысотный характер (регистрация на пяти и

более высотах) данных аэросъемок, получивших в последнее время широкое

применение на геотраверсах. При обработке и интерпретации геоданных

также следует учитывать системность физико-геологических моделей на

разных стадиях и подстадиях геологоразведочного процесса, в свою очередь

образующих систему геолого-геофизических исследований на твердые по-

лезные ископаемые, на нефть и газ, и другие виды минерального сырья.

Следовательно, анализ геоинформации развивается на базе сложной систе-

мы, включающей комплексную обработку (и интерпретацию) по разным

геолого-геофизическим методам, ее интеграцию по разным уровням зонди-

рования литосферы, и, наконец, комплексирование информации, как по ме-

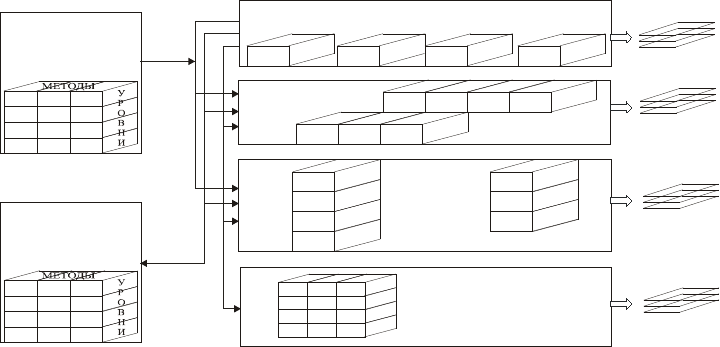
тодам, так и по уровням (рис. 10.1).

Типовая обработка данных

Обработка данных по методам

По одному уровню

Комплексная обработка

данных по методам

Интегрированная

обработка данных

по уровням

Комплексная

интегрированная

обработка данных

Геофизические

Проведение исследований

на территории

Космос

Воздух

Земля

Скважина

Геофизические

Проведение исследований

на акватории

Космос

Воздух

Океан

Скважина

Рис.10.1 Варианты анализа (обработки) геоинформации на четырех уровнях

зондирования.

К сожалению, математическая теория сложных систем только разра-

батывается. На практике системный анализ сводится к тому, что оптимизи-

руются отдельные звенья общей системы, устанавливается их влияние на

эффективность системы в целом. Оптимизация отдельных параметров ре-

альной физико-геологической модели относится к подобным задачам сис-

темного анализа. Например, можно максимизировать величину энергетиче-

ского отношения сигнал/помеха в многомерном (разнометодном и много-

уровневом) пространстве с целью решения задачи обнаружения потенци-

альной рудоносности (или нефтегазоносности) изучаемых объектов. В то же

время одновременная оптимизация всех параметров физико-геологических

моделей, помимо сложности регистрируемой информации, существенно за-

труднена из-за эквивалентности и неоднозначности решения обратных задач

разведочной геофизики.

Системный анализ всегда начинается с построения модели, отве-

чающей в нашем случае постановке конкретной геологической задачи, т.е.

формализации изучаемого объекта (процесса). Построение модели сводится

к описанию объекта (процесса) на языке математики. С помощью одной и

той же модели в принципе могут изучаться разные объекты (например, ма-

тематическая модель затухающей по экспоненте косинусоиды применяется

для описания эпейрогенеза в геологии, формы сейсмических колебаний и

характера погрешностей измерений в гравиразведке).

Обычно с помощью математических выражений удается описать не-

сложные по своему строению геологические объекты и формы геофизиче-

ских (геохимических) аномалий. Для сложных объектов необходимо ис-

пользовать статистические и стохастические модели, а их анализ проводить

на базе имитационного моделирования.

Поскольку построение модели определяется конкретной геологиче-

ской задачей, то необходим анализ модели в соответствии с постановкой

задачи исследований. При описании модели нужно провести анализ априор-

ных сведений и ограничений и сформулировать некоторую оптимизацион-

ную задачу. Так, например, при решении задач обнаружения перспективных

объектов по одному полю или по комплексу геополей можно максимизиро-

вать либо пиковое, либо энергетическое отношение сигнал/помеха в много-

мерном пространстве этих полей. Такая оптимизация (максимализация) при

разных априорных ограничениях, накладываемых на полезный сигнал и по-

меху, приводит к реализации различных по своей конструкции оптимальных

фильтров (согласованного и энергетического) при обработке данных одного

метода или приемов распознавания образов (многомерные аналоги способов

обратных вероятностей и самонастраивающейся фильтрации, метод главных

компонент и т.д.) для комплекса геополей.

Следующий этап системного анализа – решение оптимизационной

задачи (или просто оптимизация) по выбору стратегии, обеспечивающей

достижение цели управления. Критерий оптимальности при этом обычно

является и критерием отбора наиболее экономной стратегии. Например, оп-

тимальный комплекс геофизических методов при решении задачи поисков

перспективных объектов может быть выбран путем минимизации функции

потерь, включающей в себя как информационные возможности методов (в

качестве информационного признака, в частности, выступает и энергетиче-

ское отношение сигнал/помеха, рассчитываемое для любого набора геофи-

зических полей, так и их экономические показатели. Выбор оптимального

комплекса геофизических методов и определяет стратегию управления гео-

логоразведочным процессом на стадии поисков.

Таким образом, системный анализ включает построение модели, ана-

лиз этой модели и оптимизацию решения поставленной задачи [24].

Основной задачей системного анализа является установление цели, а

сама система рассматривается как механизм ее достижения.

Поскольку система наблюдений геополей на разных уровнях требует

анализа, обработки и интерпретации данных комплексных геолого-

геофизических съемок, то под интегрированным системным анализом

(ИСА) геоинформации будем понимать комплексную, интегрированную

обработку и интерпретацию разноуровневой геоинформации на основе сис-

темного анализа [4].

Цель ИСА геоинформации – создание объемных многофакторных

физико-геологических моделей изучаемых объектов (систем объектов) и

принятие управленческих решений о направлении дальнейших исследова-

ний.

Сформулируем общие положения и принципы ИСА, которые следует

использовать при разработке конкретных методов и технологий ИСА, а

также их информационного и программно-математического обеспечения.

При этом отметим, что геофизические и геохимические поля, регистрируе-

мые на разных уровнях наблюдений, обычно интерпретируются совместно

лишь в пределах того уровня, на котором они измерены. Интеграция гео-

данных (комплексная интерпретация) на разных уровнях измерений практи-

чески не используется.

До сих пор отсутствуют принципы и методы обработки и интерпре-

тации полей, зарегистрированных даже лишь на двух разных высотах. Ком-

плексный анализ и комплексная интерпретация геоданных в пределах одно-

го уровня проводятся на основе алгоритмически-программного обеспечения

распознавания образов. Комплексная интерпретация данных сейсморазвед-

ки и геофизических исследований скважин (ГИС) при решении задач сейс-

мостратиграфии и прогнозирования геологического разреза проводится на

базе тех же методов распознавания образов, причем данные ГИС обычно

используются лишь в качестве априорной информации на эталонных объек-

тах – скважинах. Совершенно очевидно, что для построения физико-

геологических моделей изучаемых объектов, адекватных реальной геологи-

ческой среде, необходимо реализовать информационные возможности мно-

гоуровневых геоданных. Поэтому актуальность разработок принципов и ме-

тодов ИСА несомненна.

Принципы ИСА вытекают из того положения, что процессы, проис-

ходящие в земной коре и на поверхности земли, взаимосвязаны. Это поло-

жение также подтверждает целостность и замкнутость всей информацион-

ной системы: космос – воздух – земля – скважина.

К основным принципам ИСА следует отнести [4]:

1) расширение территорий исследований и соответственно увеличение

объема геоинформации, относимого к элементу земной коры, при пе-

реходе с нижнего уровня на более высокий;

2) потеря глобальности исследований при переходе с верхнего на ниж-

ний уровень;

3) унаследованность проявления в физических и геохимических полях

разного уровня (от нижнего до верхнего) геологических структур и

процессов, обусловленная общей организацией структуры геологиче-

ского пространства. Эта общая организация выражается в иерархич-

ности геопроцессов, в частности, в наличии линейных и кольцевых

дислокаций земной коры, а унаследованность их проявления в полях

разного уровня связана с механизмом передачи информации с глуби-

ны на поверхность;

4) использование геоинформации, получаемой на каждом нижнем

уровне, в качестве петрофизической основы интерпретации на каж-

дом верхнем.

Так, информация о петрофизических свойствах по данным геофизи-

ческих исследований скважин используется в качестве эталонной при

решении задач прогноза литологического разреза и сейсмострати-

графии для наземных наблюдений методами сейсморазведки и дру-

гими методами.

Наземные петрофизические измерения и измерения в скважинах яв-

ляются основой для интерпретации данных с воздушных носителей.

В свою очередь аэрогеофизические и аэрогеохимические наблюдения

служат ориентиром для анализа спутниковых данных. К этому прин-

ципу относятся приемы интерполяции и экстраполяции результатов

наблюдений более детального уровня для анализа и интерпретации

данных более высокого уровня. Таким образом, этим принципом по-

стулируется наиболее рациональная схема анализа от прямого на-

блюдения объекта – наиболее детального и точного (отбор и иссле-

дование образцов пород, данных геофизических исследований сква-

жин) – к данным опосредованного наблюдения, т.е. проявления объ-

екта в физических и химических полях.

Частным случаем этого и предыдущего принципов является построе-

ние анализа от более детального (с высокой разрешающей способно-

стью) метода исследований к менее детальному, но характеризую-

щемуся большей пространственной обзорностью;

5) разбиение площади или пространства наблюдений на квазиоднород-

ные области по эффективным параметрам геосреды, значениям ком-

плексного параметра и различным статистическим показателям;

6) синэргетичность информации о соответствии с физическими основа-

ми. Каждый вид и метод прикладной геофизики характеризуется соб-

ственной геологической информативностью. Оценка этой информа-

тивности обычно реализуется «от противного», а именно, разнообра-

зием моделей объекта, неразличимых отдельным методом. В резуль-

тате использования комплекса методов возникает многообразие ото-

бражений объекта в полях различных параметров (атрибутов). Кон-

трастирование объекта от вмещающей среды обеспечивается за счет

указанного многообразия, что и представляет собой основу для ин-

тегрирования информации, полученной на разных уровнях и разны-

ми методами. Тем самым постулируется необходимость синтеза кри-

териев интерпретации комплекса геоданных;

7) адаптивность анализа геоданных. Этот принцип отражает зависи-

мость характеристик геополей (разрешающая способность, спек-

тральные и корреляционные свойства, помехоустойчивость) от теку-

щего состояния модели объекта, степени его изученности. Тем са-

мым предопределяется итеративный процесс решения задачи интег-

рированного анализа, включая динамику изменения объекта в геоло-

гическом времени и пространстве.

Последние четыре принципа важны для реализации методов интер-

претации комплексной, интегрированной геоинформации.

К принципам ИСА относятся и общие принципы самого системного

анализа: