Кутузов А.Л. Математические методы и модели исследования операций. Линейная оптимизация с помощью WinQSB и Excel
Подождите немного. Документ загружается.


Свободный формат подобен записи на чистом листе бумаги и более трудоемок. Если
выбран фиксированный формат, данные вводятся следующим образом:
После ввода данных вы вернетесь в меню функций.
Чтобы проверить правильность заданной информации, выберите в меню функций
п. 4 (просмотр данных задачи) и затем в открывшемся меню просмотра данных —
п. 1.
Если нужно задачу исправить, выберите в меню функций п. 7 (изменение задачи) и
затем в открывшемся меню изменения задачи выберите п. 1 (
д
ля изменения запасов
и потребностей) или п. 8 (для изменения затрат на перевозки). При этом программа
предложит ввести название для новой, измененной задачи.
Для сохранения задачи на диске выберите в меню функций п. 6 (сохранение задачи
на диске).
Нахождение решения
Чтобы решить задачу, выберите в меню функций п. 5 (решение задачи). Появится
меню решения, в котором можно выбрать вариант решения задачи. Оно выглядит
следующим образом:
В этом меню можно выбрать следующие варианты действий:
1.
Решение без вывода транспортных таблиц.
2.
Решение с выводом всех транспортных таблиц.
3.
Решение с выводом первой транспортной таблицы.
4.
Решение с выводом последней транспортной таблицы.
5.
Выбор метода нахождения первоначального плана.
6.
Нахождение только первоначального плана.
7.
Возврат в меню функций.
Вывод таблиц возможен только для задач, имеющих не более 4 пунктов отправления
и 5 пунктов назначения.
ПРИМЕЧАНИЕ
Если выбран вариант решения с выдачей промежуточных таблиц, то процесс можно в любой момент
Ст
р
. 81 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
прервать, нажав клавишу F9
Для решения нашего примера выберем п. 1 (Решение без вывода транспортных
таблиц).
Ниже меню решения появится сообщение программы о том, что решение найдено:
The optimal solution has been found.
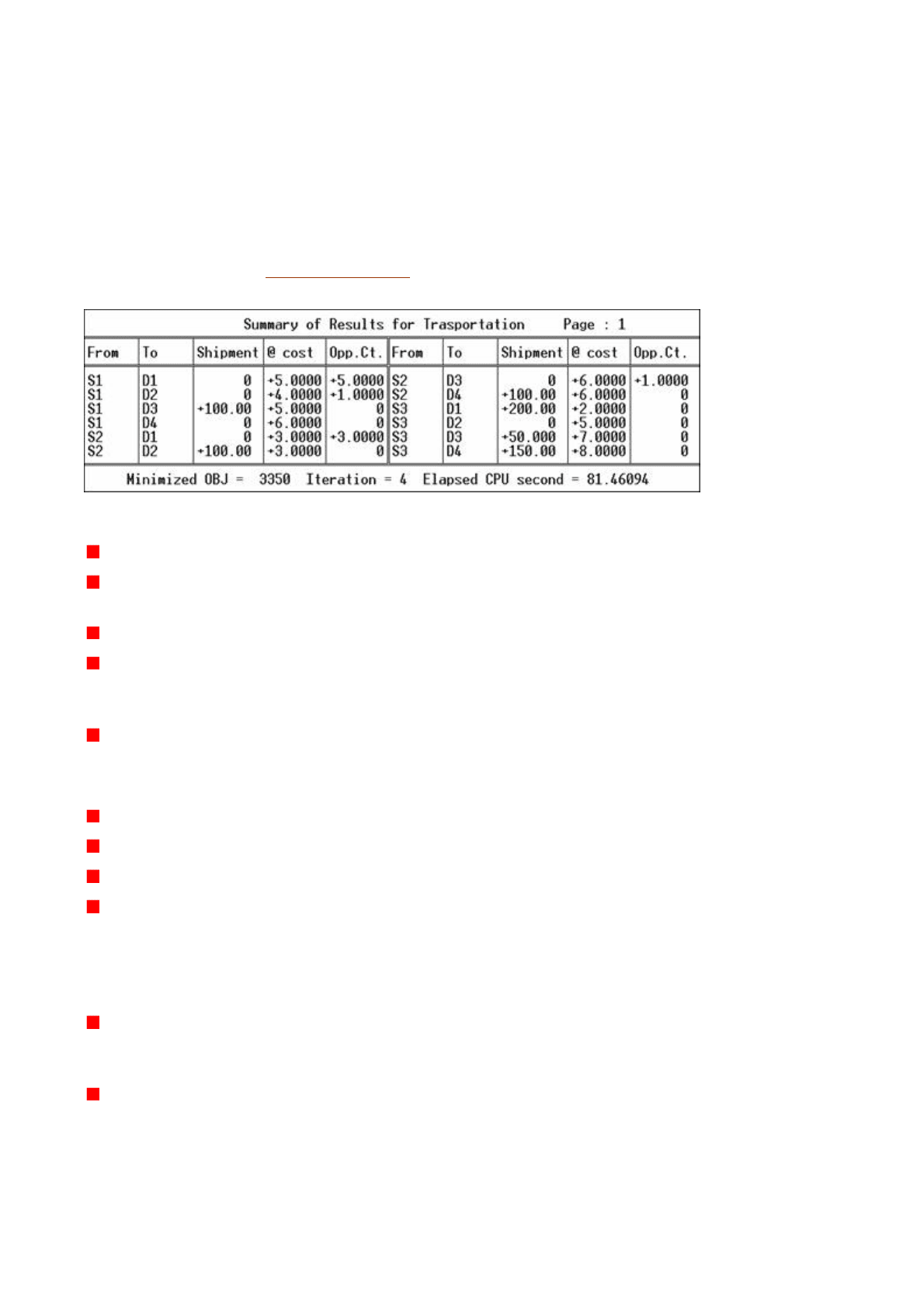
Перейдя на следующую страницу, вы увидите меню результатов, аналогичное тому,
которое используется при целочисленном решении задачи линейного
программирования (см. раздел 2.4.4). Выбрав в нем п. 1, вы получите следующую
таблицу с результатами решения:
В этой таблице выводится следующая информация:
В столбцах From и To — названия пунктов отправления и назначения.
В столбце Shipment — количество груза, которое следует перевозить из каждого
пункта отправления в каждый пункт назначения.
В столбце @ cost — затраты на перевозку единицы груза.
В столбце
Opp.Ct.
— двойственные оценки, показывающие, на какую величину
увеличатся общие затраты, если уйти от оптимального плана, добавив в него
перевозку единицы груза в указанном направлении.
В последней строке таблицы — общие затраты (Minimized OBJ = 3350), число
итераций и время работы процессора.
После просмотра результатов вы вернетесь в меню функций, где можно:
изменить условия текущей задачи, если выбрать п. 7 (изменение задачи);
ввести новую задачу, если выбрать п. 2 (ввод новой задачи);
выйти из программы, если выбрать п. 9 (выход в меню программ);
выйти из пакета, выбрав п. 10 (выход из QSB+/или QS).
Частные случаи решения транспортной задачи с помощью QSB+ и QS
При решении транспортных задач с помощью пакетов QSB+ и QS могут встретиться
следующие частные случаи:
Если перевозки груза характеризуются не затратами, а выручкой или прибылью,
то транспортная задача оформляется так же, как в описанном выше примере, но
целевая функция максимизируется.
Если суммарные запасы груза не равны суммарные потребностям (задача не
сбалансирована), задание параметров и ввод данных происходят точно так же, но
программа автоматически добавит фиктивный пункт отправления или назначения.
В таблице с результатами такие пункты обозначаются словом Dummy (фиктивный).
Перевозки, которые в оптимальном плане должны быть выполнены с фиктивного
пункта отправления или на фиктивный пункт назначения, на самом деле
Ст
р
. 82 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

осуществляться не будут. Они означают следующее: перевозка с фиктивного пункта
отправления на реальный пункт назначения — объем недопоставки груза на пункт
назначения, а перевозка с реального пункта отправления на фиктивный пункт
назначения — объем груза, оставшегося на пункте отправления.
Если какие-либо маршруты перевозок недопустимы, то соответствующие затраты
следует положить равными достаточно большим числам, значительно
превышающим затраты остальных перевозок. Можно также ввести вместо этих
затрат латинскую букву
M
, если целевая функция минимизируется или –
M
, если
минимизируется.
Если по условию задачи необходимо получить целочисленное решение, то для
этого необходимо обеспечить, чтобы запасы груза в пунктах отправления и
потребности в пунктах назначения выражались целыми числами (это особенность
алгоритма решения транспортной задачи).
Самостоятельная работа
1.
Воспроизведите на своем компьютере с помощью пакета прикладных программ
QSB+ всю последовательность решения примера, рассмотренного выше
(см. раздел 3.3.1).
2.
Решите примеры 3.1.1, 3.2.1 и 3.2.2 с помощью пакета прикладных программ
QSB+.
3.3.2. Решение транспортной задачи с помощью программы Excel
Программа Excel позволяет оформить решение транспортной задачи в виде
наглядных таблиц, удобных как для работы, так и для демонстрации полученных
результатов (в отличие от решения с помощью пакетов прикладных программ).
Ввод данных
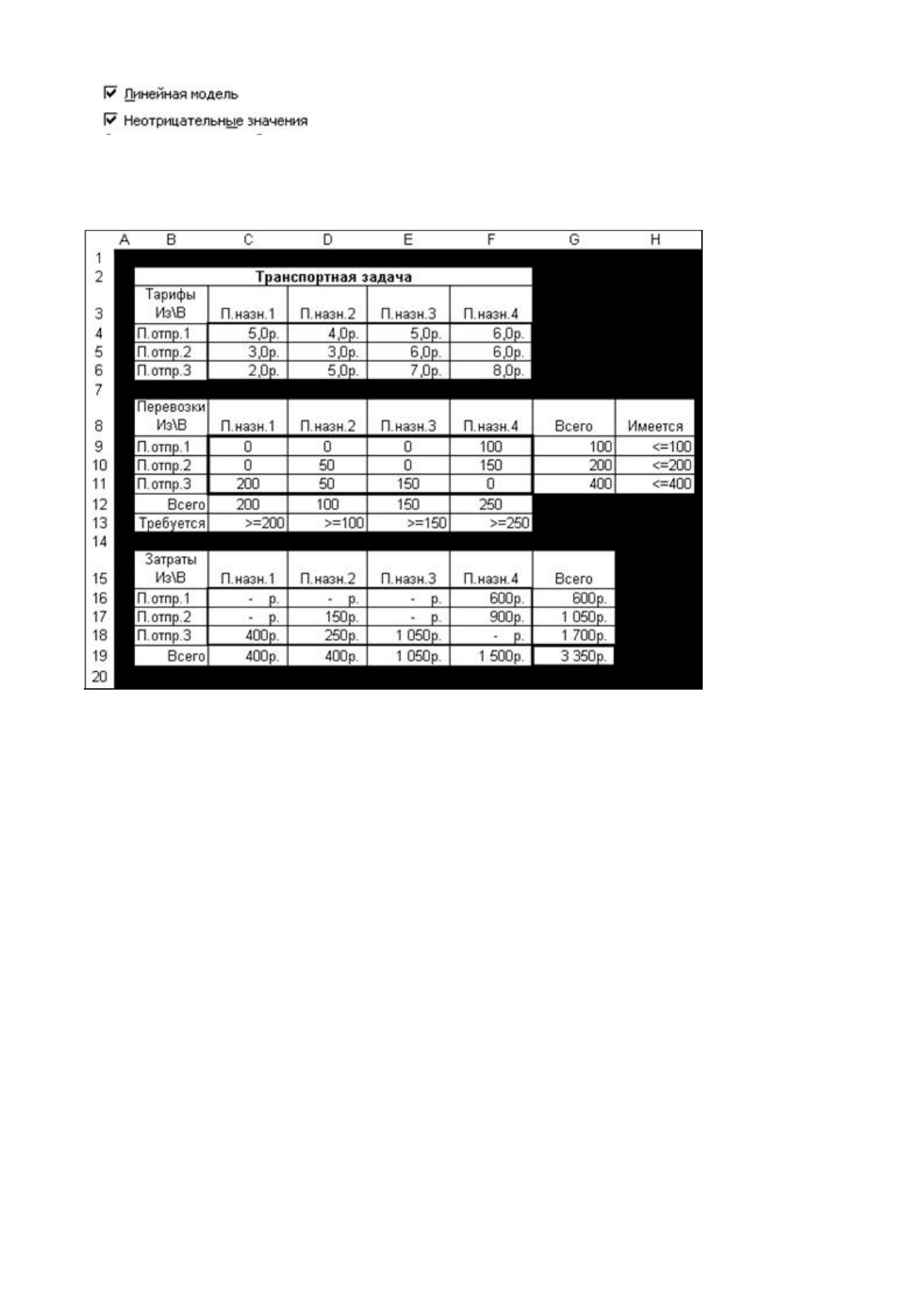
Рабочий лист Excel при решении транспортной задачи на компьютере выглядит
следующим образом:
Как мы видим, модель оформлена в виде трех таблиц. Затраты на перевозку
Ст
р
. 83 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

единицы груза вводятся в первую из них, а запасы в пунктах отправления и
потребности в пунктах назначения — во вторую, в ячейки H9:H12 и C13:F13.
Остальные значения вычисляются по формулам, указанным в следующей таблице:
ПРИМЕЧАНИЕ
При оформлении таблиц в ячейки, не используемые в таблицах, добавлена заливка черного цвета.
Запасы и потребности в ячейках H9:H12 и C13:F13 отображаются вместе со знаками неравенства
СОВЕТ
Вместо знаков равенства в ограничениях модели, сформулированной в разделе 3.1, лучше
использовать знаки неравенства, даже когда задача сбалансирована (запасы грузов и потребности
совпадают). Знаки неравенства показывают, что на каждый пункт назначения должно быть доставлено
не меньше груза, чем требуется (знак >=), а из каждого пункта отправления может быть вывезено не
больше груза, чем имеется
(знак <=). Использование знаков неравенства делает формулировку задачи
более общей, поскольку точно так же формулируется и несбалансированная задача, когда запасы
грузов превышают потребности в них.
Чтобы создать формат отображения чисел вместе со знаками неравенства:
1.
Выделите ячейки для форматирования, щелкните их правой кнопкой мыши и в
появившемся контекстном меню выберите команду Формат ячеек.
2.
В появившемся окне на вкладке Число в списке Числовые форматы выберите пункт
(все форматы).
3.
В списке Тип выберите формат Основной.
4.
В поле
Тип
измените код этого формата на
"<="Основной
или
">="Основной
.
5.
Щелкните кнопку OK для применения созданного формата к выделенным ячейкам
и сохранения его для дальнейшего использования.
Использование средства поиска решений подробно описано в разделе 2.4.3. Здесь
же мы лишь кратко напомним основные моменты.
В окне
Поиск решения
задается следующая информации:
В окне Параметры поиска решения следует задать следующие параметры:
Ячейка Форм
у
ла Копировать в
C16 =C4*C9 C16:F18
G9 =СУММ(C9:F9) G10:G11; G16:G19
C12 =СУММ(C9:C11) D12:F12; C19:F19
Ст
р
. 84 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
Анализ результатов
Обратимся еще раз к рабочему листу решения транспортной задачи с помощью
Excel, который был впервые представлен в предыдущем разделе:
Обратите внимание на вторую таблицу. Здесь в жирной рамке отображено
оптимальное решение нашей задачи.
В третьей таблице вычисляются затраты на перевозки по отдельным пунктам
отправления и назначения, а в ячейке G19 — целевая
функция (общие затраты).
План перевозок несколько отличается от полученного в предыдущем разделе, хотя
целевые функции совпадают. Это объясняется тем, что транспортные задачи могут
иметь множество оптимальных планов при одинаковых общих издержках.
Чувствительность решения транспортной задачи можно проанализировать с
помощью отчета по устойчивости, он выглядит так:
Ст
р
. 85 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
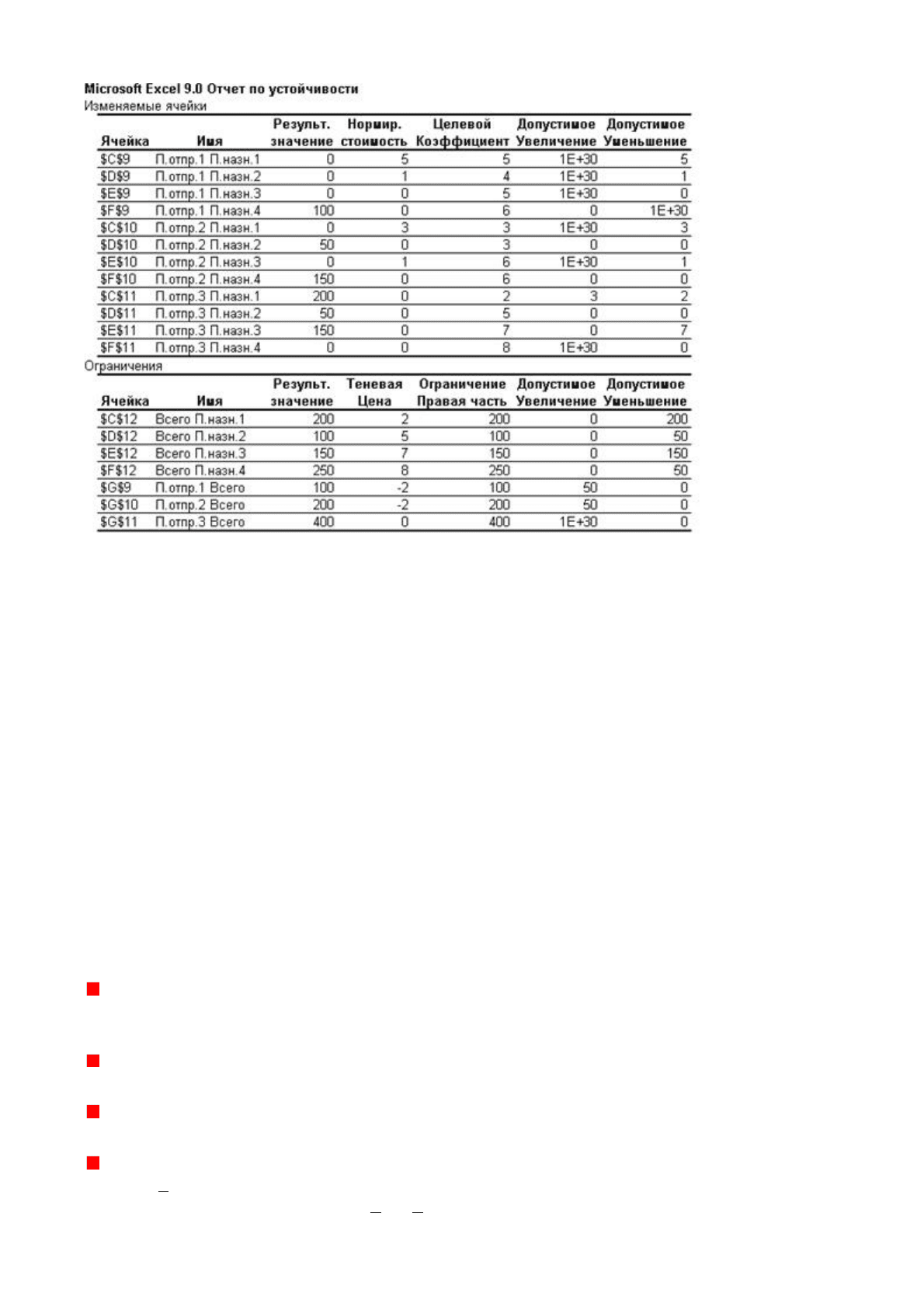
Из первой таблицы отчета по устойчивости видно, на какую величину следует
снизить затраты на перевозку в неиспользуемых направлениях, чтобы перевозить
грузы в этих направлениях стало выгодно.
Например, затраты на перевозку единицы груза из 1-го пункта отправления во 2-й
пункт назначения должны быть сокращены на 1 р., чтобы это направление стало
привлекательным.
Вторая таблица отчета показывает, насколько можно снизить общие затраты за счет
уменьшения потребностей в пунктах назначения или увеличения запасов в пунктах
отправления (изменения в противоположном направлении недопустимы, так ка
к
приводят к превышению потребностей над запасами и делают задачу
неразрешимой).
Например, если на несколько единиц (до 150) уменьшить потребности в 3-м пункте
назначения, то на каждую единицу общие затраты снизятся на 7 р.
А
если на
несколько единиц (до 50) увеличить запасы во 2-м пункте отправления, то на каждую
единицу общие затраты снизятся на 2 р.
Частные случаи решения транспортной задачи с помощью Excel
При решении транспортных задач с помощью программы Excel могут встретиться
следующие частные случаи:
Если перевозки груза характеризуются не затратами, а выручкой или прибылью,
то транспортная задача оформляется так же, как в описанном выше примере, но
целевая функция максимизируется.
Если суммарные запасы груза превышают суммарные потребности,
формулировка модели не меняется.
Если суммарные потребности превышают суммарные запасы груза, можно
действовать двумя способами:
Первый способ: в ограничениях на количество отправляемых грузов поменяйте
знак < на = (все запасы будут израсходованы), а в ограничениях на количество
доставляемых грузов — знак > на < (не все потребности будут удовлетворены).
Ст
р
. 86 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

Второй способ: введите фиктивный пункт отправления, условно приписав ему
недостающий запас грузов. Затраты на перевозки из этого пункта на любой пункт
назначения можно положить равными 0 или штрафу за недопоставку единицы
груза на данный пункт назначения (в возможности минимизации штрафных
санкций за недопоставку грузов — преимущество второго способа действий).
Любая полученная в оптимальном решении поставка с фиктивного пункта
отправления трактуется как недоставленный груз.
Если какие-либо маршруты перевозок недопустимы, то соответствующие затраты
следует положить равными достаточно большим числам, значительно
превышающим затраты остальных перевозок (или, если задача на максимум,
большим по абсолютной величине отрицательным числам).
Если по условию задачи необходимо получить целочисленное решение, то для
этого необходимо обеспечить, чтобы запасы груза в пунктах отправления и
потребности в пунктах назначения выражались целыми числами (это особенность
алгоритма решения транспортной задачи).
Самостоятельная работа
1.
Воспроизведите на своем компьютере с помощью программы Excel всю
последовательность решения примера, рассмотренного в этом разделе
(см. раздел 3.3.2).
2.
Повторите на своем компьютере решение примеров 3.1.1, 3.2.1 и 3.2.2 с помощью
пакета прикладных программ Excel.
3.
Пусть в примере 3.2.2 введены штрафы в размере $200 и $300 за каждый
недопоставленный автомобиль в распределительные центры Денвера и Майами
соответственно. Кроме того, поставки из Лос-
А
нджелеса в Майами не планируются
изначально. Постройте транспортную модель и найдите схему оптимальных
перевозок с помощью программы Excel.
Глава 4. Задача о назначениях
В общих чертах, задача о назначениях — это задача о наилучшем распределении
некоторого количества работ между исполнителями. Она сводится к задаче
линейного программирования и, по сути, является частным случаем транспортной
задачи. Любое ее решение будет целочисленным.
4.1. Общий вид задачи о назначениях
Итак, требуется оптимально распределить n исполнителей (или каких-то других
объектов) по n работам. Такая задача встает перед менеджером в самых
разнообразных ситуациях. Вот несколько примеров: распределение торговых агентов
по районам, представителей сферы обслуживания по поступившим заявкам на
обслуживание, редакторов по редактируемым рукописям, дизайнеров по
создаваемым рекламным плакатам и т. д.
Считается, что каждый работник может выполнять любую работу, но с разной
степенью мастерства (или с разной производительностью, или за разное время).
Оптимальность при этом достигается, если для каждой работы удается подобрать
лучшего работника. Например, если на каждую работу назначается работник той
квалификации, которая нее необходима, то стоимость выполнения работы будет
ниже, чем при назначении работника неподходящей квалификации.
Цель задачи — найти распределение работников, обеспечивающее минимальную
суммарную стоимость выполнения всех работ (или максимальную суммарную
Ст
р
. 87 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

производительность, или минимальное суммарное время). Работники при решении
этой задачи считаются неделимыми в том смысле, что не могут выполнять несколько
работ. Каждый из них назначается только на одну из них.
Исходные данные для решения задачи о назначениях могут быть представлены в
виде следующей таблицы:
Величина c
ij
равна стоимости назначения работника i на работу j (i, j = 1, 2, , n). Здесь
предполагается, что количество работников совпадает с количеством работ.
Когда количество исполнителей не совпадает с количеством работ
В том случае, когда количество исполнителей не совпадает с количеством работ,
задача становится несбалансированной. Однако ее можно сделать
сбалансированной.
Д
ля этого вводят недостающее количество фиктивных
исполнителей или фиктивных работ, точно так же, как это делалось в транспортной
задаче. Стоимости назначения фиктивных исполнителей на работы (или реальных
исполнителей на фиктивные работы) полагают равными нулю. Затем задачу решают,
как обычную задачу о назначениях.
Полученное оптимальное решение интерпретируется следующим образом. Если в
найденном решении окажется, что фиктивный исполнитель должен выполнить какую-
то работу, то на самом деле эта работа выполняться не будет. Если же на фиктивную
работу будет назначен реальный исполнитель, то в реальности этот исполнитель
останется без работы.
Если исполнитель не может выполнить работу
Если по условию задачи какой-то исполнитель не может
выполнить определенную
работу, нужно положить стоимость назначения этого исполнителя на эту работу
равной очень большому числу, значительно превышающему все остальные
стоимости назначений.
В этом случае программа решения задачи на компьютере автоматически исключит
это назначение из решения как невыгодное.
Задача о назначениях — частный случай транспортной задачи
Как уже отмечалось ранее задача о назначениях —
частный случай транспортной
задачи, в которой работники соответствуют пунктам отправления, а работы —
пунктам назначения.
Все запасы на пунктах отправления и заявки, поданные пунктами назначения, в
данном случае считаются равными 1.
Стоимость перевозки единицы груза с пункта оправления i на пункт назначения
j
равна c
ij
, то есть стоимости назначения работника i на работу j.
С учетом этих замечаний, задачу о назначениях решают точно так же, как и
Работы
1 2 n
1
c
11
c
12
c
1
n
1
2 c
21
c
22
c
2
n
1
Работники . . . . .
. . . . .
. . . . .
n c
n
1
c
n
2
c
nn
1
1 1 1
Ст
р
. 88 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

транспортную.
4.1.1 Простой пример задачи о назначениях
Трое подростков (Джон, Том и Билл) подрабатывают во время каникул, предлагая
ж
ителям дачного поселка разнообразные услуги по уборке территории и уходу за
автомобилями. Хозяин одного из дачных домиков очень загружен по работе, поэтому
решил поручить выполнение трех работ (стрижка газона, уборка гаража и мойка
машины) этим ребятам. Поскольку работы должны быть выполнены быстро, один
подросток не успеет выполнить несколько работ. Ребята работают независимо друг
от друга и потому плата, которую они просят за свою работу, различается. Хозяин
домика встретился с каждым из них индивидуально и выяснил их расценки, поместив
их в следующую таблицу:
Основываясь на этой информации, как следует хозяину домика распределить работы
между ребятами, чтобы общие затраты были минимальными?
ПРИМЕЧАНИЕ
Для данного примера намеренно выбрана простая задача, решение которой можно найти и без
математического моделирования, просто взглянув на таблицу. Но в реальных ситуациях количество
исполнителей и работ может быть значительно больше и без математических расчетов в таких случаях
не обойтись.
Теперь давайте сформулируем задачу о назначениях. Прежде всего, введем
переменные x
ij
, где i — номер исполнителя (i = 1, 2, 3), а j — номер работы (j = 1, 2, 3).
Пусть переменная x
ij
= 1, если i-й исполнитель назначен на j-ю работу, и x
ij
= 0 в
противном случае.
Обозначив целевую функцию (общие затраты) через z, построим математическую
модель задачи:
Минимизировать z = 15x
11
+ 10x
12
+ 9x
13
+ 9x
21
+ 15x
22
+ 10x
23
+ 10x
31
+ 12x
32
+ 8x
33
при ограничениях
где x
ij
∈
[0, 1], где i
∈
[1, 3], j
∈
[1, 3].
Левые три ограничения означают, что каждый из подростков выполняет только одну
работу (не может выполнять несколько работ одновременно), а правые три — что
каждая работа выполняется только одним школьником (на нее нельзя назначить
сразу нескольких исполнителей).
Все ограничения выражены в виде равенств, поскольку количество исполнителей
равно количеству работ.
Оптимальное решение (значения переменных x
ij
, полученные с помощью программы
Excel) представлено в следующей таблице:
Ст
р
ижка газона
(
1
)
Убо
р
ка га
р
ажа
(
2
)
Мойка машины
(
3
)
Джон
$15 $10 $9
Том
$9 $15 $10
Билл
$10 $12 $8
x
11
+ x
12
+ x
13
= 1,
x
21
+ x
22
+ x
23
= 1,
x
31
+ x
32
+ x
33
= 1,
x
11
+ x
21
+ x
31
= 1,
x
12
+ x
22
+ x
32
= 1,
x
13
+ x
23
+ x
33
= 1,
Ст
р
. 89 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
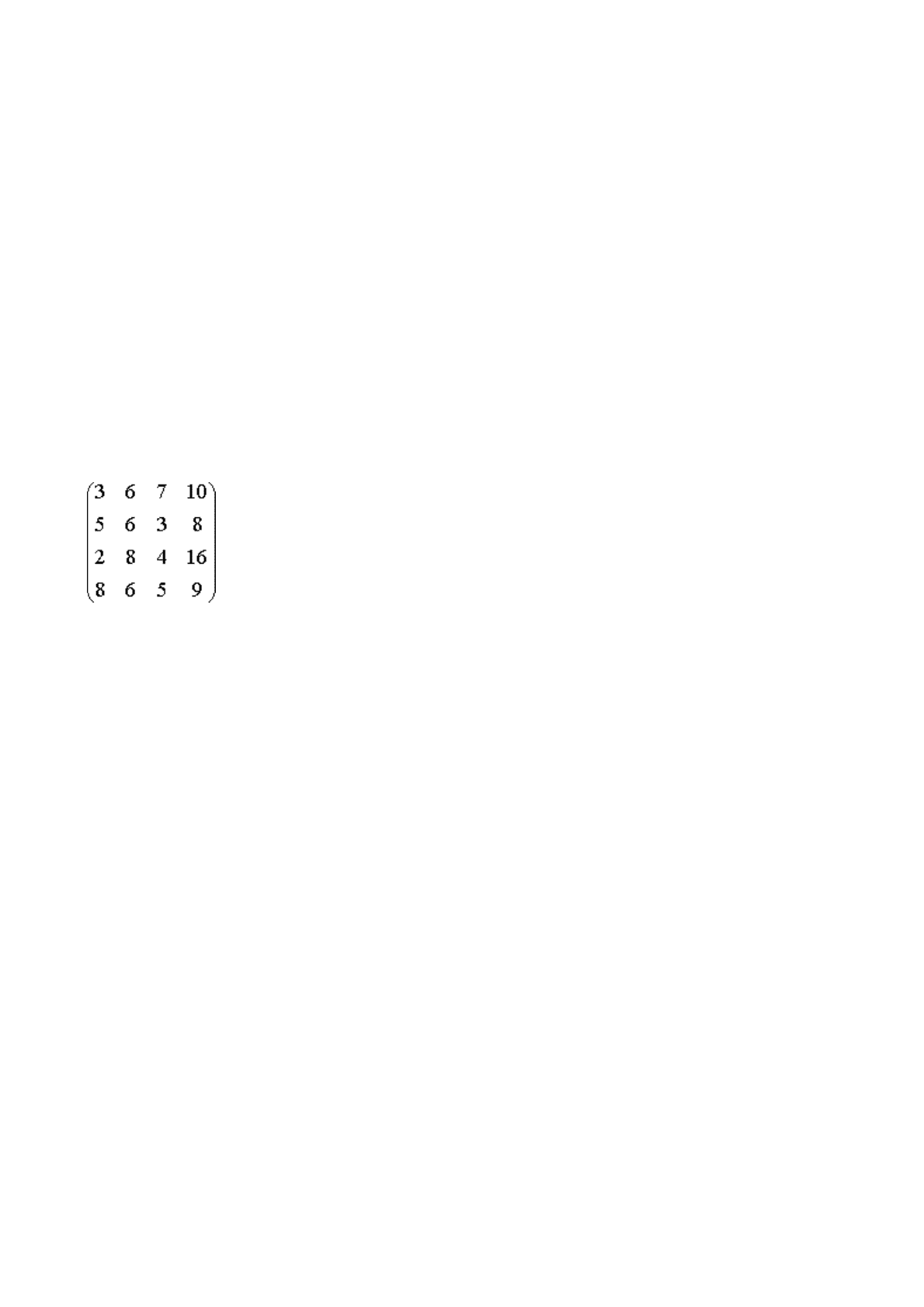
Итак, мы получили следующее оптимальное решение нашей задачи:
Джон будет убирать в гараже,
Том — подстригать газон,
Биллу достанется мойка машины.
Эта работа обойдется хозяину домика в 9 + 10 + 8 = $27.
4.2. Решение задачи о назначениях на компьютере
Давайте решим следующую задачу.
Д
ля выполнения четырех видов работ выделено
четыре человека. Время выполнения каждой работы каждым исполнителем задано
матрицей, номер строки которой соответствует номеру исполнителя, а номер
столбца — номеру работы:
Необходимо так распределить исполнителей по работам, чтобы общие затраты
времени были минимальны.
Построим сначала математическую модель данной задачи.
Пусть переменная x
ij
= 1, если i-й исполнитель назначен на j-ю работу, и x
ij
= 0 в
противном случае.
Обозначим целевую функцию (общие затраты времени) через F.
Тогда математическая модель задачи будет выглядеть следующим образом:
F = 3x
11
+ 6x
12
+ 7x
13
+ 10x
14
+ 5x
21
+ 6x
22
+ 3x
23
+ 8x
24
+
+ 2x
31
+ 8x
32
+ 4x
33
+ 16x
34
+ 8x
41
+ 6x
42
+ 5x
43
+ 9x
44
→
min,
где x
ij
∈
[0, 1], где i
∈
[1, 4], j
∈
[1, 4].
ПРИМЕЧАНИЕ
Аналогично ставится и решается задача, где назначению i-го исполнителя на j-ю работу соответствуют,
вместо времени, затраты каких-либо других ресурсов или определенная эффективность (прибыль,
производительность). В последнем случае ищется максимум целевой функции.
4.2.1. Решение задачи о назначениях с помощью пакетов QSB+ и QS
Ст
р
ижка газона
(
1
)
Убо
р
ка га
р
ажа
(
2
)
Мойка машины
(
3
)
Джон
0 1 0
Том
1 0 0
Билл
0 0 1
x
11
+ x
12
+ x
13
+ x
14
= 1,
x
21
+ x
22
+ x
23
+ x
24
= 1,
x
31
+ x
32
+ x
33
+ x
34
= 1,
x
41
+ x
42
+ x
43
+ x
44
= 1,
x
11
+ x
21
+ x
31
+ x
41
= 1,
x
12
+ x
22
+ x
32
+ x
42
= 1,
x
13
+ x
23
+ x
33
+ x
43
= 1,
x
14
+ x
24
+ x
34
+ x
44
= 1,
Ст
р
. 90 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
