Кутузов А.Л. Математические методы и модели исследования операций. Линейная оптимизация с помощью WinQSB и Excel

Подождите немного. Документ загружается.

модели.

В настоящем разделе анализ чувствительности проводиться на базе графического

решения задачи линейного программирования. Рассмотрим отдельно два следующих

случая:

изменение коэффициентов целевой функции;

изменение значений констант в правой части неравенств ограничений.

Конечно, проведенное здесь исследование будет элементарным и ограниченным,

однако, оно пояснит основные идеи методов анализа чувствительности.

2.3.1. Изменение коэффициентов целевой функции

В общем виде целевую функцию задачи линейного программирования с двумя

переменными можно записать следующим образом:

Максимизировать (или минимизировать) z = c

+ c

Если мы будем менять значений коэффициентов c

и c

, то в результате будем

получать изменение угла наклона прямой z. Если мы теперь обратимся к разделу 2.2,

где рассматривался графический способ решения задачи линейного

программирования, то увидим, что изменение угла наклона прямой z может привести

к изменению оптимального решения. Оно будет достигаться в другой угловой точке

области допустимых решений. Однако (внимание!), очевидно, существуют такие

интервалы изменения коэффициентов c

и c

, где текущее оптимальное решение

сохраняется. Задача анализа чувствительности и состоит в получении такой

информации.

В частности, представляет интерес определение интервала оптимальности для

отношения c

. (или, что то же самое, для c

). Интервалом оптимальности будет

называться такой интервал, для которого оптимальное решение в данной модели

сохраняется неизменным, если значение отношения c

не выходит за пределы

этого интервала.

Давайте теперь рассмотрим на примере задачи о производстве краски, как на деле

проводится анализ чувствительности. Для этого рассмотрим рисунок, где

воспроизведена снова область допустимых решений для этой задачи.

Ст

. 31 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

На рисунке видно, что функция z = 5x

+ 4x

остигает максимального значения в

угловой точке C.

При изменении же коэффициентов целевой функции z = c

+ c

точка C останется

точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать

между углами наклона двух прямых, пересечением которых является точка C. Этими

прямыми являются:

+ 4x

= 24 (ограничение на сырье M1),

+ 2x

= 6 (ограничение на сырье М2).

Математически это можно записать следующим образом:

, где c

≠

или , где c

≠

В первой системе неравенств условие c

≠ 0 означает, что прямая, соответствующая

целевой функции, не может быть горизонтальной. Аналогичное условие (а именно

≠

0) во второй системе неравенств означает, что эта же прямая не может быть

вертикальной.

Из нашего рисунка видно, что интервал оптимальности данной задачи (он

определяется двумя прямыми, пересекающимися в точке C) не разрешает целевой

функции быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы

получили две системы неравенств, определяющих интервал

оптимальности в нашем

примере.

ВНИМАНИЕ

Если c

и c

могут принимать нулевые значения, интервал оптимальности для отношения c

. (или

Ст

. 32 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

) просто разбивают на два множества, где это не происходит.

Итак, если коэффициенты c

и c

удовлетворяют приведенным выше неравенствам,

оптимальное решение будет достигаться в точке С.

Отметим, если прямая z = c

+ c

совпадет с прямой x

+ 2x

= 6, то оптимальным

решением будет любая точка отрезка CD. Аналогично, если прямая,

соответствующая целевой функции, совпадет с прямой 6x

+ 4x

= 24, тогда любая

точка отрезка BC будет оптимальным решением. Однако заметим, что в обоих

случаях точка C остается точкой оптимального решения.

Неравенства, приведенные выше, можно использовать при определении интервала

оптимальности для какого-либо одного коэффициента целевой функции, если

предположить, что другой коэффициент остается неизменным. Так, если в наше

модели зафиксировано значение коэффициента c

(пусть c

= 4), тогда интервал

оптимальности для коэффициента с

получаем из неравенств

путем подстановки туда значения c

= 4.

После выполнения элементарных арифметически операций получаем неравенства

для коэффициента c

2 ≤ c

≤ 6.

Аналогично, если зафиксировать значение коэффициента c

(например, c

= 5), тогда

из неравенств

получаем интервал оптимальности для коэффициента c

10/3 ≤ c

≤ 10.

Самостоятельная работа

Определите графически интервал оптимальности для отношения c

следующих задачах. Отдельно рассмотрите те особые случаи, когда

коэффициенты c

и c

могут обращаться в нуль.

Максимизировать z =2x

+ 3x

при выполнении условий

+ 2x

≤ 5,

–x

+ x

≤ 0,

, x

≥ 0.

Максимизировать z =4x

+ 3x

при выполнении условий

+ 5x

≤ 5,

– x

≤ 0,

Ст

. 33 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

, x

≥ 0.

Максимизировать z =x

+ x

при выполнении условий

–x

+ x

≤ 0,

– x

≤ 3,

, x

≥ 0.

В задаче о диете проделайте следующее:

Определите интервал оптимальности для отношения стоимости фунта кукурузной

муки к стоимости фунта соевой муки.

Будет ли оптимальным ранее найденное решение, если стоимость фунта

кукурузной муки увеличится на 20%, а стоимость фунта соевой уменьшится на 5%,

то?

Если стоимость фунта кукурузной муки останется фиксированной (30 центов), а

стоимость фунта соевой муки возрастет до $1.10, то останется ли оптимальным

ранее найденное решение?

2.3.2. Изменение правых частей ограничений

Во многих моделях линейного программирования ограничения трактуются ка

условия ограниченности ресурсов. В таких ограничениях правая часть неравенств

является верхней границей количества доступных ресурсов. В настоящем разделе

мы изучим чувствительность оптимального решения к изменению ограничений,

накладываемых на ресурсы.

Такой анализ задачи линейного программирования предлагает простую меру

чувствительности решения, называемую стоимостью единицы ресурса; при

изменении количества доступных ресурсов (на единицу) значение целевой функции в

оптимальном решении изменится на стоимость единицы ресурса.

Рассмотрим на примере этот вид анализа задачи линейного программирования.

Давайте вернемся опять к задаче о производстве краски. В разделе 2.1 мы построили

математическую модель этой задачи. Она имела вид:

Максимизировать z = 5x

+ 4x

при выполнении ограничений

+ 4x

≤

24,

+ 2x

≤

– x

+ x

≤

≥

0, x

≥

В этой модели первые два неравенства представляют собой ограничения на

использование сырья M1 и М2, соответственно.

авайте теперь определим

стоимость единиц этих ресурсов.

Ресурс M1

Начнем с ограничения для сырья M1. Напомним, что в данной задаче оптимальное

решение достигается в угловой точке С, являющейся точкой пересечения прямых,

Ст

. 34 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

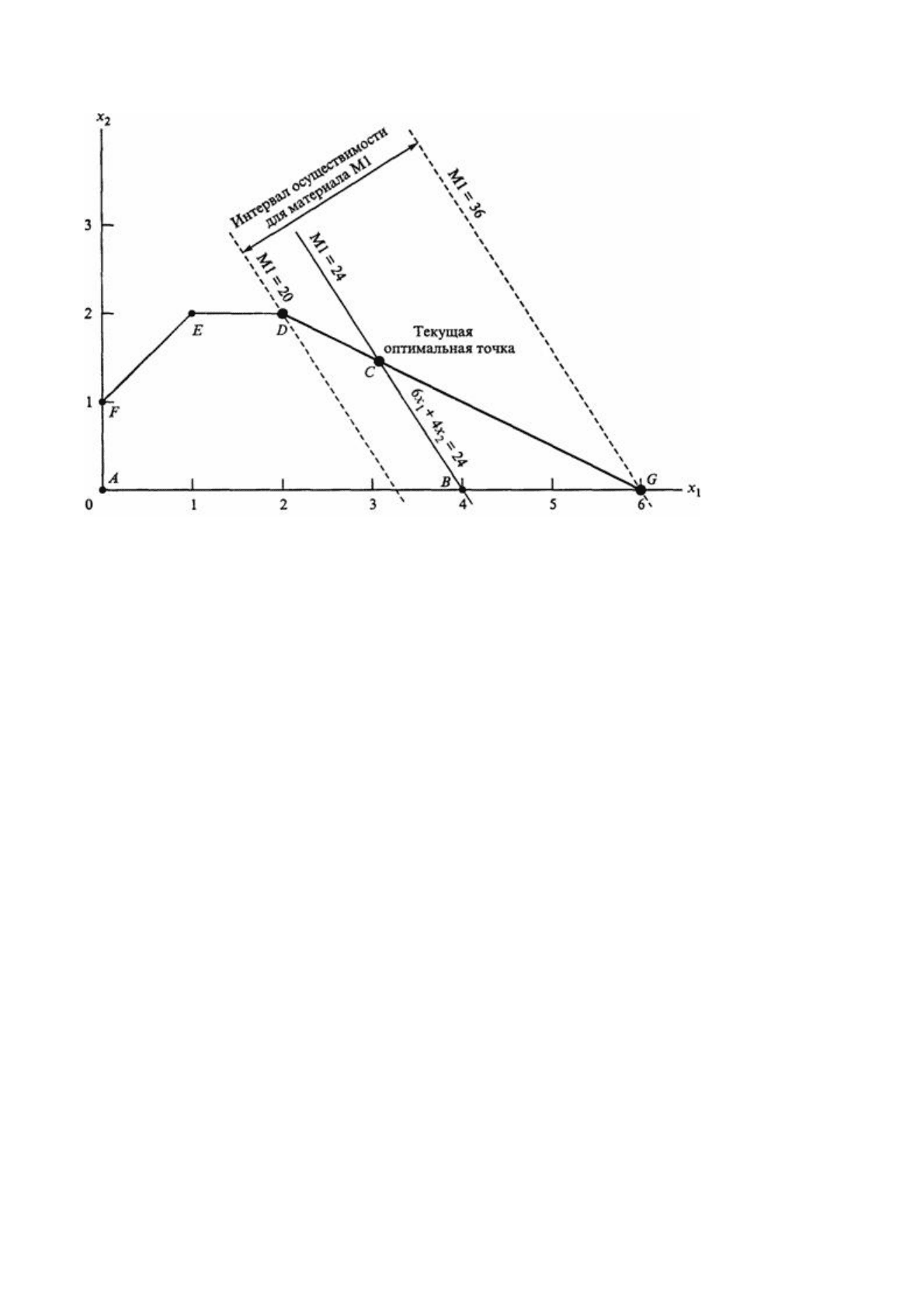
соответствующих ограничениям на сырье M1 и М2.

Как видно из рисунка, при изменении уровня доступности материала M1 (увеличение

или уменьшение текущего уровня, равного 24 т) точка C оптимального решения

«плывет» вдоль отрезка DG. Любое изменение уровня доступности материала M1,

приводящее к выходу точки пересечения C за пределы этого отрезка, ведет

неосуществимости оптимального решения в точке C.

Поэтому можно сказать, что конечные точки D = (2, 2) и G = (6, 0) отрезка DG

определяют интервал осуществимости (другое его название — интерва

устойчивости) для ресурса M1.

Количество сырья M1, соответствующего точке D = (2,2), будет следующим:

+ 4x

= 6

2 + 4

2 = 20 т.

Аналогично, количество сырья M1, соответствующего точке G = (6, 0), равно

6 + 4

0 = 36 т.

Таким образом, интервал осуществимости для ресурса M1 составляет 20 ≤ M

≤ 36

(здесь через М

обозначено количество материала M1).

Если мы определим М

как М

= 24 + D

, где D

— отклонение количества материала

M1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как

20 ≤ 24 + D

≤ 36 или –4 ≤ D

≤ 12.

Это означает, что текущий уровень ресурса M1 может быть уменьшен не более чем

на 4 т и увеличен не более чем на 12 т. В этом случае гарантируется, что

оптимальное решение будет достигаться в точке C — точке пересечения прямых,

соответствующих ограничениям на ресурсы M1 и М2.

Давайте теперь вычислим стоимость единицы материала М1. При изменении

количества сырья M1 от 20 до 36 тонн, значения целевой функции z будут

соответствовать положению точки C на отрезке DG. Обозначив через у

стоимость

единицы ресурса M1, получим следующую формулу:

Ст

. 35 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

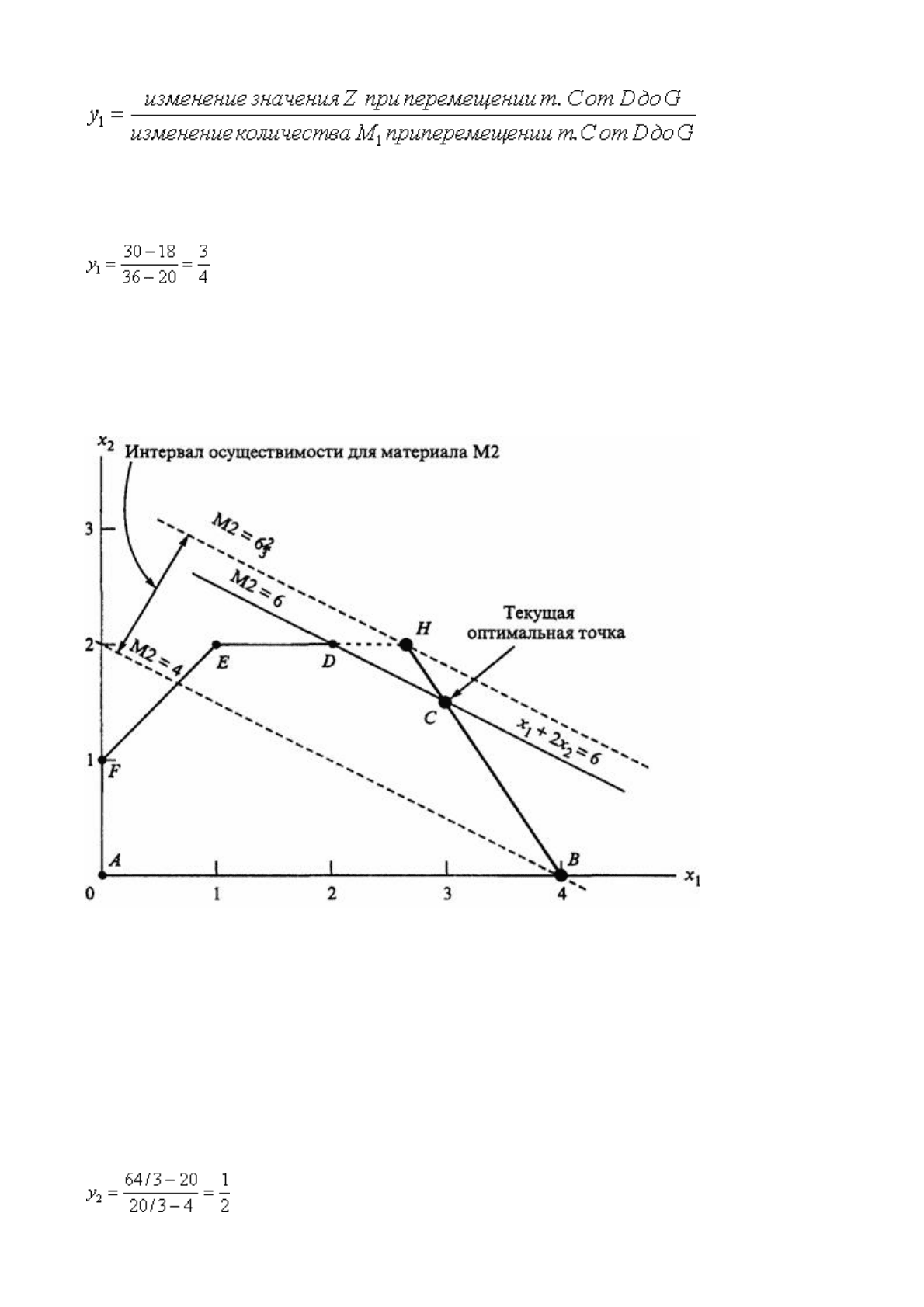
Если точка C совпадает с точкой D = (2, 2), то z = 5

2 + 4

2 = 18 (тысяч дол ларов),

если же точка C совпадает с точкой G = (6, 0), тогда z = 5

6 + 4

0 = 30 (тысяч

долларов). Отсюда следует, что

(тысяч долларов на тонну материала M1).

Этот результат показывает, что изменение количества ресурса M1 на одну тонну

(если общее количество этого ресурса не меньше 20 и не больше 36 тонн) приводит

изменению в оптимальном решении значения целевой функции на $750.

Ресурс M2

Теперь рассмотрим ресурс М2.

На нашем рисунке видно, что интервал осуществимости для ресурса М2

определяется точками B и H отрезка BH, где B = (4, 0) и H = (8/3, 2). Точка

находится на пересечении прямых ED и BC.

Находим, что количество сырья М2, соответствующего точке B, равно x

+ 2x

= 4 + 2

0 = 4 т, а точке H — 8/3 +2

2= 20/3 т.

Значение целевой функции в точке В равно 5x

+ 4x

= 5

4 + 4

0 = 20 (тысяч

долларов), а в точке H — 5

8/3+4

2= 64/3 (тысяч долларов).

Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн, а

стоимость единицы ресурса М2, обозначенная как y

, равна

(тысяч долларов на тонну материала М2).

Ст

. 36 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

Самостоятельная работа

Рассматривается задача: фабрика производит два типа ковбойских шляп.

Производство шляпы первого типа требует в два раза больше временных

ресурсов, чем производство шляпы второго типа. Если фабрика будет производить

только шляпы второго типа, то в день она сможет изготовить 400 таких шляп.

Рынок накладывает ограничения на производство шляп: не более 150 шляп

первого типа и 200 шляп второго типа. Прибыль от производства шляп составляет

$8 на единицу первого типа и $5 — второго типа. Проделайте следующее:

Примените графический метод для определения ежедневного оптимального

производства шляп обоих типов.

Определите стоимость возрастания производства на одну шляпу второго типа и

интервал значений числа ежедневного производства этих шляп, для которого

данная стоимость была бы применима.

Используя метод стоимости единицы ресурса, определите, на сколько изменится

максимальная прибыль фабрики, если ежедневное производство шляп первого

типа не будет превышать 120 единиц.

Чему равна стоимость возрастания предельного спроса на одну шляпу второго

типа?

Рассматривается задача о производстве двух видов продукции (А и В). Объем

продаж продукта А составляет не менее 80% от общего объема продаж продуктов

А и В. Вместе с тем компания не может производить более 100 единиц продукта А

в день. Для производства этих продуктов используется одно и то же сырье,

поступление которого ограничено 240 фунтами в день. На изготовление единицы

продукта А расходуется 2 фунта сырья, а единицы продукта В — 4 фунта. Цена

одной единицы продуктов А и В составляет $20 и $50, соответственно.

Найдите оптимальную структуру производства этой компании.

Определите стоимость единицы сырья и интервал изменения потребляемого

сырья, при котором справедлива данная стоимость.

С помощью графического анализа чувствительности определите, как изменится

значение целевой функции при изменении максимального уровня производства

продукта А на ±10 единиц.

2.4. Решение задачи линейного программирования на

компьютере

Как мы уже отмечали ранее, алгоритмы задач принятия решений настолько сложны,

что без применения компьютера реализовать их практически невозможно. Компьютер

с помощью программного обеспечения реализует алгоритмы поиска оптимального

решения, которые преобразуют исходные данные в искомый результат.

Рассмотрим на примере задачи производственного планирования, как решить задачу

линейного программирования с помощью пакетов QSB+ и QS, а также с помощью

программы Excel. Сначала рассмотрим, как получить решение этой задачи симплекс-

методом, при котором решения могут оказаться нецелочисленными, а затем решим

эту же задачу в целочисленном виде.

2.4.1. Задача производственного планирования

Итак, рассмотрим такую задачу. Предприятие выпускает четыре вида продукции (1, 2,

3 и 4). На изготовление этой продукции расходуются трудовые ресурсы, сырье и

финансы. С учетом рыночного спроса и производственно-технологических

Ст

. 37 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

возможностей заданы предельные границы выпуска каждого вида продукции. Эти

границы, наличие и нормы расхода ресурсов, а также маржинальная прибыль

(разность между выручкой и переменными издержками), которую при реализации

приносит предприятию единица продукции каждого вида, приведены в следующей

таблице:

Наша задача — определить план выпуска четырех видов продукции,

обеспечивающий максимальную прибыль от ее реализации.

Сначала, как и всегда, строим математическую модель задачи.

Обозначим количество выпускаемых изделий через x

, x

Обозначим целевую функцию (валовую маржинальную прибыль) — через F.

Тогда математическую модель нашей задачи будет иметь вид:

F = 70x

+ 60x

+ 110x

+ 140x

→

max,

2.4.2. Решение задачи линейного программирования с помощью

пакетов QSB+ и QS

ВНИМАНИЕ

Пакеты прикладных программ QSB+ или QS не русифицированы. Поэтому при описании работы с ними

приводятся не сами команды, а их перевод.

Выбор программы

После запуска QSB+ или QS дважды нажмите любую клавишу.

Появится меню программ, имеющихся в пакете (для пакета QSB+ это меню

представлено на следующем рисунке:

Рес

ур

сы П

од. 1 П

од. 2 П

од. 3 П

од. 4 Наличие

Трудовые 1 2 1 2 19

Сырье 7 4 5 4 80

Финансы 5 7 9 8 100

Прибыль 70 60 110 140

Нижн. гр. 3 1 1 2

Верхн. гр. 5 3 4

+ 2x

+ x

+ 2x

≤

19,

+ 4x

+ 5x

+ 4x

≤

80,

+ 7x

+ 9x

+ 8x

≤

100,

≤

Ст

. 38 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

Выберите в этом меню п. 1 (линейное программирование), если работаете в QSB+,

или п. 2 (с тем же названием), если работаете в QS.

В результате откроется меню функций, представленное на следующем рисунке:

В этом меню можно выбрать следующие варианты действий:

Описание программы линейного программирования.

Ввод новой задачи (она заменит текущую задачу).

Загрузка задачи, ранее сохраненной на диске (она заменит текущую задачу).

Просмотр данных задачи.

Решение задачи.

Сохранение задачи на диске.

Изменение задачи.

Просмотр результатов решения (перед этим должен быть выбран п. 5 — решение

задачи).

Выход в меню программ.

10.

Выход из QSB+ (или QS).

Задачу можно сохранить на диске, а впоследствии загрузить с него. Это позволяет

избежать повторного ввода данных при следующем сеансе работы. Имя файла при

сохранении задается в виде xxxxxxxx.xxx. Можно выбрать любой из двух

предлагаемых форматов сохранения: MPS и стандартный (для выбора формата MPS

введите латинскую букву

, в противном случае — латинскую букву

. Файл

записывается в ту же папку, в которой находится пакет QSB+ (или QS).

Ст

. 39 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

При загрузке ранее сохраненного файла нужно указать его имя и формат (если

формат — MPS, введите латинскую букву

, в противном случае — латинскую букву

). Если имя и формат файла указаны правильно, появится сообщение

Your problem

has been read

, после которого нажмите клавишу Page Down.

Задание параметров поиска решения

Чтобы ввести параметры решения задачи линейного программирования, выберите

сначала в меню функций п. 2 (ввод новой задачи). Затем, в ответ на запрос

программы, введите название решаемой задачи, например, назовем нашу задачу

Production

На следующей странице в угловых скобках (в порядке сверху вниз) задайте

параметры модели, как это показано на следующем рисунке:

На этой странице (в ее нижней части) задаются следующие параметры:

максимизировать (

) или минимизировать (

) целевую функцию;

количество переменных (без учета искусственных или дополнительных);

количество ограничений;

примерный процент ненулевых элементов матрицы ограничений (для небольших

задач можно не задавать);

использовать стандартные имена переменных X1…Xn (

) или задавать другие

имена (

);

вводить данные в свободном (

) или фиксированном (

) формате (свободный

формат подобен записи на чистом листе бумаги и более трудоемок);

задавать граничные условия в фиксированном формате (

) или нет (

) (если

введено значение

, граничные условия не задаются и все переменные считаются

неотрицательными).

Допустимая размерность задачи зависит лишь от объема памяти вашего компьютера.

Так, реально могут решаться задачи, имеющие сотни переменных и ограничений, но

при этом нужно обязательно указать примерный процент ненулевых элементов

матрицы ограничений (по умолчанию — 5%).

Ввод числовых данных

Если выбран фиксированный формат ввода данных, на следующей странице вы

увидите форму для ввода числовых коэффициентов при переменных (в целевой

Ст

. 40 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm