Кутузов А.Л. Математические методы и модели исследования операций. Линейная оптимизация с помощью WinQSB и Excel

Подождите немного. Документ загружается.

очень важна для анализа оптимального решения.

нализ изменений коэффициентов целевой функции в данном случае не имеет

особого смысла, поскольку в этой модели они естественным образом имеют

единственное возможное значение 1. Если бы целевая функция отражала какую-

нибудь другую «цель» (например, минимизировала бы стоимость эксплуатации

автобусов), тогда ситуация могла быть иной и анализ этих коэффициентов имел бы

смысл.

Самостоятельная работа

Решите задачу данного раздела с помощью пакета QSB+ и проверьте, совпадают ли

решения, полученные с помощью программы Excel и с помощью пакета QSB+.

(Решения могут и различаться, поскольку, как отмечалось, задача имеет множество

оптимальных решений и разные программы могут находить разные решения — в

силу некоторых незначительных различий в используемом алгоритме.) Сопоставьте

приведенную в данном разделе информацию, выдаваемую в отчете по устойчивости

программы Excel, и информацию итогового отчета QSB+.

2.5.5. Разрезка бумаги

Бумажная фабрика производит стандартные рулоны бумаги шириной в 20 футов.

Специальные заказы клиентов требуют разрезания стандартных рулонов. Типовой

заказ (такие заказы могут меняться каждый день) приведен в следующей таблице:

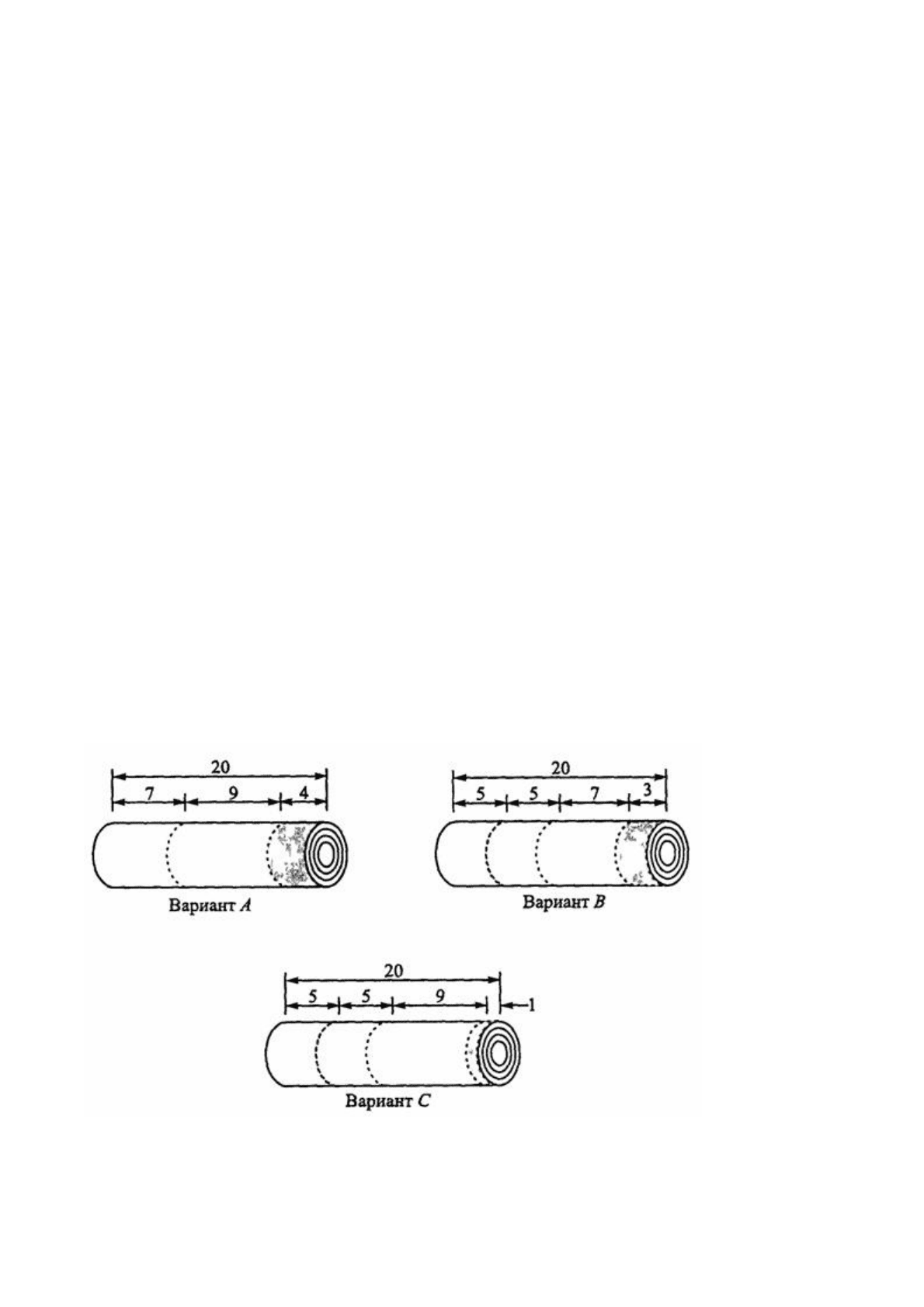
На фабрике заказы выполняются путем разрезания стандартных рулонов на

требуемые части специальными ножами. Существует несколько вариантов разрезки

стандартного рулона, три из которых показаны на следующем рисунке:

Конечно, существуют и другие варианты, не представленные на этом рисунке (они

будут описаны ниже), но сейчас мы ограничимся только представленными (А, В и С).

Для выполнения заказа можно совместно использовать несколько вариантов

разрезки стандартных рулонов. Например, для выполнения заказа, приведенного в

Позиции заказа Требуемая ширина

ру

лона

(

фу

ты

)

Требуемое количество

ру

лонов

(

шт.

)

1 5 150

2 7 200

3 9 300

Ст

. 71 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

таблице, можно применить следующие комбинации вариантов А, В и С:

Разрезать 300 стандартных рулонов, используя вариант А, и 75 рулонов с

помощью варианта В.

Разрезать 200 стандартных рулонов, используя вариант А, и 100 рулонов с

помощью варианта С.

Какая из этих комбинаций лучше? Чтобы ответить на этот вопрос, надо рассмотреть

потери от каждой из комбинаций. На нашем рисунке отходы бумаги после каждого

варианта разрезки располагаются от правого края каждого рулона до первой

пунктирной линии.

Мы можем оценить преимущества каждой комбинации, если подсчитаем суммарные

отходы, полученные после их применения. Но поскольку отрезки рулонов, идущие в

отходы, имеют разную длину, нам надо подсчитать объем этих отходов, а не просто

количество отрезков.

Предполагая, что стандартный рулон бумаги имеет площадь поперечного сечения,

равную L квадратным футам, подсчитываем потери для комбинаций 1 и 2:

комбинация 1: 300×(4×L) + 75×(3×L) = 1425L куб. футов,

комбинация 2: 200×(4×L) + 100×(1×L) = 900L куб. футов.

Если число рулонов шириной 5, 7 или 9 футов, которые были получены в результате

применения какой-либо комбинации вариантов разрезки, превышает количество,

необходимое для выполнения заказа, то разность между ними также следует отнести

к потерям.

В первой комбинации при использовании варианта A получено 300 – 200 = 100

лишних рулонов шириной 7 футов; применение варианта B добавляет еще 75 лишних

рулонов такой же ширины. Таким образом, дополнительные потери составляют 175×

(7×L) = 1225L куб. футов.

Во второй комбинации не производится лишних рулонов шириной 7 и 9 футов, но

применение варианта C приводит к появлению 200 – 150 = 50 лишних рулонов

шириной 5 футов, что составляет 50×(5×L) = 250L куб. футов дополнительных

отходов бумаги. В результате этих выкладок имеем следующее:

объем отходов от 1-й комбинации = 1425L + 1225L = 2650L куб. футов,

объем отходов от 2-й комбинации = 900L + 250L = 1150L куб. футов.

Очевидно, что вторая комбинация лучше, так как имеет меньше отходов.

Для получения оптимального решения данной задачи необходимо определить все

допустимые варианты разрезки стандартных рулонов и затем получить ее все

возможные комбинации этих вариантов. Хотя определить все допустимые варианты

разрезки несложно, перебор всех комбинаций этих вариантов уже является

нетривиальной задачей. Здесь необходим систематический подход к организации

такого перебора. В данном случае это может выполнить задача линейного

программирования.

Математическая модель

Мы должны найти комбинацию вариантов разрезки (переменные), с помощью

которой можно было бы выполнить заказ (ограничения) с наименьшими отходами

бумаги (целевая функция).

Переменные надо определить таким образом, чтобы их значения можно было бы

интерпретировать в способ разрезки стандартных рулонов бумаги. Поэтому

определим переменные как количество стандартных рулонов,

азрезанных

Ст

. 72 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

помощью конкретных вариантов разрезки. Это определение требует описания всех

возможных вариантов разрезки. Три варианта показаны на приведенном выше

рисунке, другие возможные варианты приведены в следующей таблице:

Убедитесь, что не пропущены еще какие-нибудь варианты разрезки, при этом

помните, что в допустимом варианте разрезки ширина остатка стандартного рулона

должна быть меньше 5 футов.

Теперь можно определить переменные: x

— количество стандартных рулонов,

разрезанных вариантом j, где j = 1, 2,..., 6.

Ограничением в этой модели является требование того, что произведенных рулонов

заданных размеров (5, 7 и 9 футов) будет достаточно для выполнения заказа. Если

использовать все варианты разрезки, приведенные в таблице, то получим

количество рулонов шириной 5 футов = 2x

+ 2x

+ 4x

+ x

количество рулонов шириной 7 футов = x

+ x

+ 2x

количество рулонов шириной 9 футов = x

+ x

+ 2x

Эти числа должны быть не меньше 150,200 и 300, соответственно.

Для построения целевой функции заметим, что общий объем отходов можно

подсчитать как разность между объемом всех использованных стандартных рулонов

и объемом рулонов, необходимых для выполнения заказа. Запишем это следующим

образом:

объем использованных стандартных рулонов = 20L(x

+ x

объем заказных рулонов = L(150 × 5 + 200 × 7 + 300 × 9) = 4750L.

Поскольку объем рулонов, необходимых для выполнения заказа, постоянен, а также

постоянна величина поперечного сечения L, целевую функцию можно записать

просто как сумму всех переменных:

z = x

+ x

Таким образом, получаем следующую задачу линейного программирования:

Минимизировать z = x

+ x

при выполнении условий

+ 2x

+ 4x

+ x

≥

150 (ограничение на рулоны шириной 5 футов),

+ x

+ 2x

≥

200 (ограничение на рулоны шириной 7 футов),

+ x

+ 2x

≥

300 (ограничение на рулоны шириной 9 футов),

≥

0, j=1,2, ..,6.

Оптимальное решение этой задачи представлено на следующем рисунке:

Треб. ширина

(

фу

ты

)

ва

2 вар. 3 вар. 4 вар. 5 вар. 6 вар. Треб.

кол.

ру

л.

5 0 2 2 4 1 0 150

7 1 1 0 0 2 0 200

9 1 0 1 0 0 2 300

Остаток (футы) 4 3 1 0 1 2

Ст

. 73 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

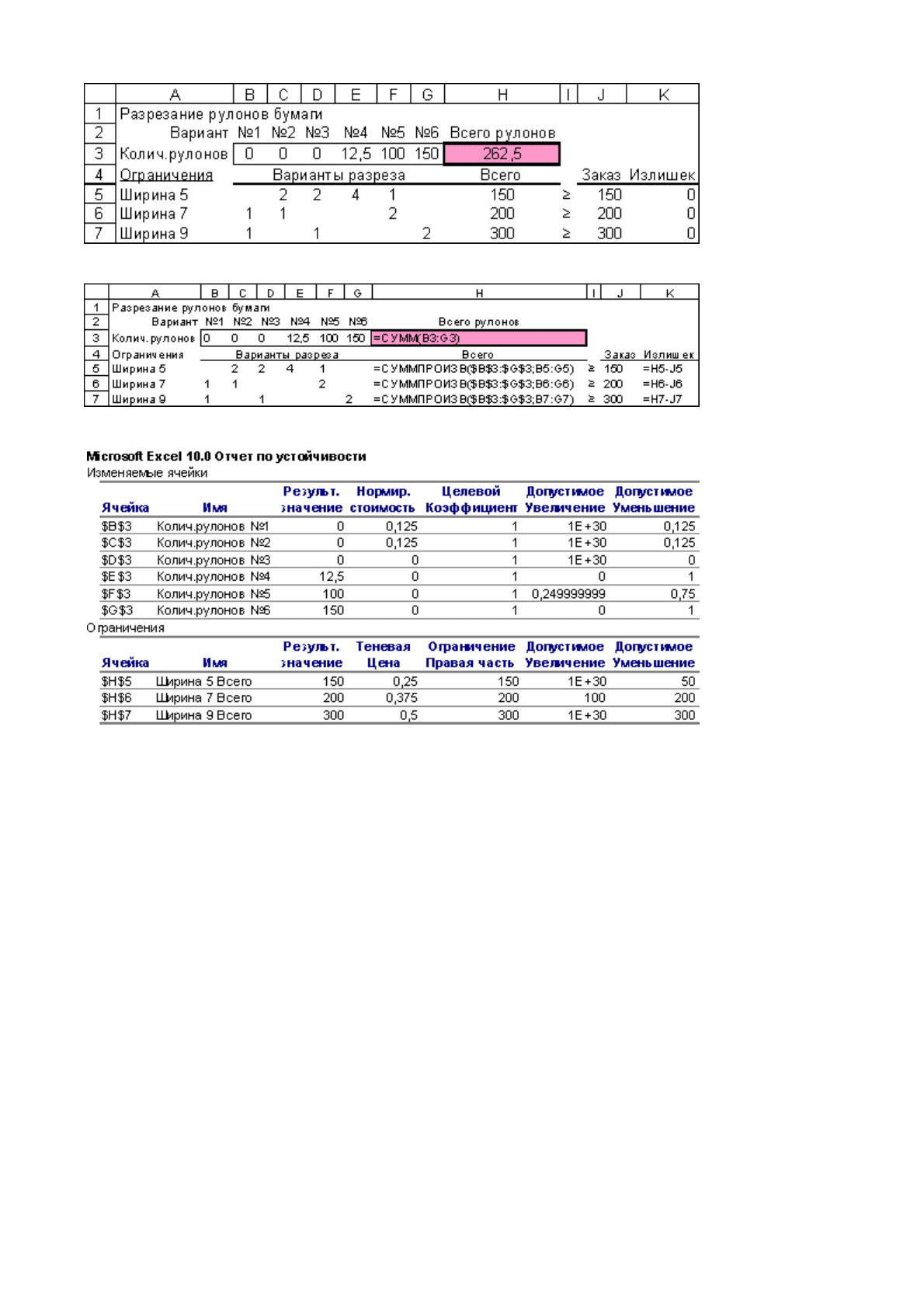
Отчет по устойчивости показывает, что задача имеет и другие оптимальные решения,

где для выполнения заказа используется такое же количество рулонов стандартной

длины, но применяются другие варианты разрезки. Действительно, нормированная

стоимость, соответствующая переменной x

равна нулю, хотя сама переменная

имеет нулевое значение. Следовательно, в оптимальном решении эта переменная

может быть увеличена на 1 без изменения целевой функции.

В приведенном решении 12,5 стандартных рулонов разрезаются в соответствии с

вариантом 4, 100 стандартных рулонов — в соответствии с вариантом 5 и 150

стандартных рулонов — с вариантом 6. В таком виде это решение нельзя

реализовать, так

как значение переменной x

нецелое. В этой ситуации можно

применить алгоритм целочисленного программирования или округлить значение

переменной x

до 13.

При интерпретации результатов, полученных с помощью программы Excel, следует

учитывать требование целочисленности значений переменных, которое неявно

присутствует в данной задаче. Например, теневая цена 0,25, соответствующая

первому ограничению, показывает, что увеличение на 1 количества заказных рулонов

шириной 5 футов потребует дополнительно еще четверти стандартного рулона

(шириной 20 футов). Но эта информация в данном случае не имеет практического

смысла. Ее нужно переформулировать, исходя из условия целочисленности :

потребуется дополнительный стандартный рулон при увеличении на 4 единицы

количества заказных рулонов шириной 5 футов. Подобные переформулировки

Ст

. 74 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

следует сделать и при интерпретации других теневых цен.

Самостоятельная работа

Решите задачу данного раздела с помощью пакета QSB+ и проверьте, совпадают ли

решения, полученные с помощью программы Excel и с помощью пакета QSB+.

(Решения могут различаться, поскольку, задача имеет множество оптимальных

решений — как и задача предыдущего раздела.) Сопоставьте приведенную в данном

разделе информацию, выдаваемую в отчете по устойчивости программы Excel, и

информацию итогового отчета QSB+.

Глава 3. Транспортная задача

В предыдущих разделах мы описали некоторые общие подходы к решению задач

линейного программирования. Однако существуют частные типы задач линейного

программирования, которые, в силу своей особой структуры, решаются иначе. К

таким задачам относятся транспортная задача и задача о назначениях.

3.1. Общий вид транспортной задачи

Транспортная задача — задача о наиболее рациональном плане перевозо

однородного продукта из пунктов производства в пункты потребления.

Назначение транспортной задачи — определение объемов перевозок из пунктов

отправления в пункты назначения с минимальной суммарной стоимостью перевозок.

При этом должны учитываться ограничения, накладываемые на объемы грузов,

имеющихся в пунктах отправления (предложения), и ограничения, учитывающие

потребность грузов в пунктах назначения (спрос).

В транспортной модели предполагается, что стоимость перевозки по какому-либо

маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту.

В общем случае транспортную модель можно применять для описания ситуаций,

связанных:

с управлением запасами,

управлением движением капиталов,

составлением расписаний,

назначением персонала и др.

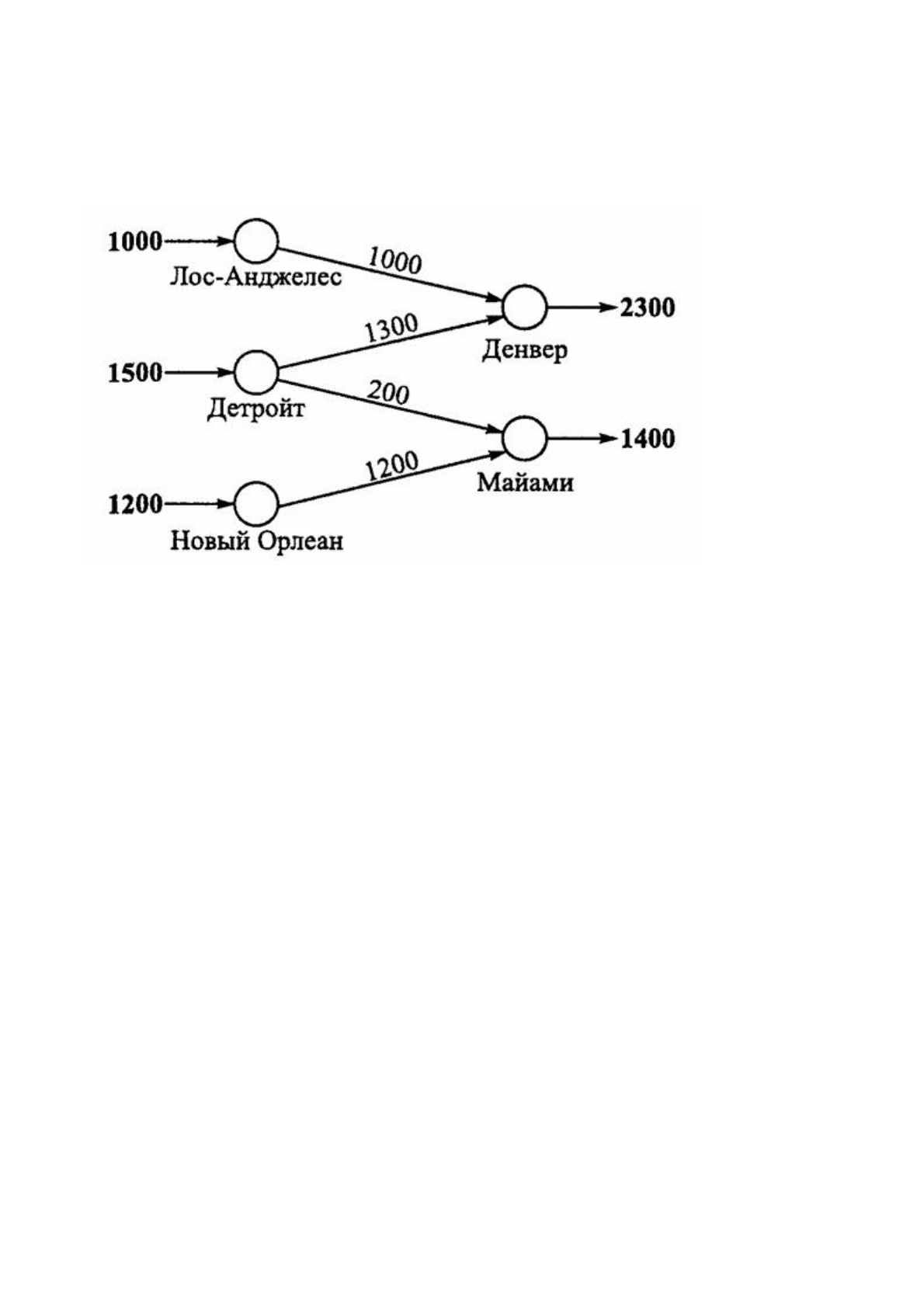
Представление транспортной задачи в виде сети с m пунктами отправления и n

пунктами назначения, которые показаны в виде узлов сети,

ано на следующем

рисунке:

Ст

. 75 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

Здесь линии (назовем их дугами), соединяющие узлы сети, соответствуют

маршрутам, связывающим пункты отправления и назначения.

С дугой (i, j), соединяющей пункт отправления i с пунктом назначения j, соотносятся

два вида данных:

стоимость с

перевозки единицы груза из пункта i в пункт j;

количество перевозимого груза x

Объем грузов в пункте отправления i равен a

, а объем грузов в пункте назначения

— b

Задача формулируется следующим образом:

Определить неизвестные величины x

, минимизирующие суммарные транспортные

расходы и удовлетворяющие ограничениям, накладываемым на объемы грузов в

пунктах отправления (предложения) и пунктах назначения (спрос).

3.1.1 Перевозка автомобилей (спрос равен предложению)

Автомобильная компания имеет три завода в Лос-Анджелесе, Детройте и Новом

Орлеане и два распределительных центра в Денвере и Майами. Объемы

производства заводов компании в следующем квартале составят соответственно

1000, 1500 и 1200 автомобилей. Ежеквартальная потребность распределительных

центров составляет 2300 и 1400 автомобилей. Расстояния (в милях) между заводами

и распределительными центрами приведены в следующей таблице:

Транспортная компания оценивает свои услуги в 8 центов за перевозку одного

автомобиля на расстояние в одну милю. В результате получаем следующую

стоимость перевозок (с округлением до доллара) по каждому маршруту:

Основываясь на этих данных, формулируем следующую задачу линейного

программирования:

Минимизировать z = 80x

+ 215x

+ 100x

+ 108x

+ 102x

+ 68x

при ограничениях

+ x

= 1000 (Лос-Анджелес),

+ x

= 1500 (Детройт),

+ x

= 1200 (Новый Орлеан),

+ x

= 2300 (Денвер),

+ x

= 1400 (Майами),

≥

0, где i = 1,2, 3, j = 1,2.

енве

Майами

Лос-Анджелес

1000 2690

Детройт

1250 1350

Новый Орлеан

1275 850

енве

(

)

Майами

(

)

Лос-Андж. (1)

$80 $215

Детройт (2)

$100 $108

Нов. Орлеан (3)

$102 $68

Ст

. 76 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

Эти ограничения выражены в виде равенств, поскольку общий объем произведенных

автомобилей (= 1000 + 1500 + 1200 = 3700) равен суммарному спросу

распределительных центров (= 2300 + 1400 = 3700).

Данную задачу линейного программирования можно решить симплекс-методом.

Оптимальное решение (полученное на компьютере) показано на следующем рисунке:

Итак, оптимальное решение предполагает перевозку 1000 автомобилей из Лос-

Анджелеса в Денвер, 1300 автомобилей — из Детройта в Денвер, 200 автомобилей

— из Детройта в Майами и 1200 — из Нового Орлеана в Майами. Минимальная

стоимость перевозок составляет $313 200.

3.2. Несбалансированные транспортные задачи

В тех случаях, когда суммарный объем предложений (грузов, имеющихся в пунктах

отправления) не равен общему объему спроса на товары (грузы), запрашиваемые

пунктами назначения, транспортная модель называется несбалансированной.

Далее мы последовательно будем применять прием, позволяющий любую

несбалансированную транспортную задачу сделать сбалансированной. Для этого

будем вводить фиктивные пункты назначения или отправления. Выполнение

баланса транспортной задачи необходимо для того, чтобы иметь возможность

применить алгоритм решения, используемый на компьютере.

Примеры несбалансированных задач буду рассмотрены в следующих двух пунктах.

3.2.1 Перевозка автомобилей (спрос превышает предложение)

Давайте рассмотрим конкретный пример несбалансированной задачи. Возьмем за

основу задачу из предыдущего пункта и предположим, что завод в Детройте

уменьшил выпуск продукции до 1300 автомобилей (вместо 1500, как было ранее). В

этом случае общее количество произведенных автомобилей (= 3500) меньше общего

количества заказанных (= 3700) автомобилей. Таким образом, очевидно, что часть

заказов распределительных центров Денвера и Майами не будет выполнена.

Поскольку в данной ситуации спрос превышает предложение, для восстановления

баланса введем фиктивный завод (пункт отправления), производящий 200 (= 3700 –

3500) автомобилей.

Назначим нулевую стоимость транспортных перевозок от фиктивного завода до

пунктов назначения, поскольку такого завода не существует. В принципе, стоимость

Ст

. 77 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

транспортных перевозок от фиктивного пункта назначения может иметь любое

положительное значение. Например, чтобы гарантировать выполнение всех заказов

распределительного центра Майами, можно назначить очень высокую стоимость

перевозок (штраф) от фиктивного завода до Майами.

Сбалансированная модель и ее оптимальное решение, полученное с помощью

компьютера, представлены в следующей таблице:

Оптимальное решение показывает, что фиктивный завод поставит в Майами 200

автомобилей. Это означает, что для данного распределительного центра из заказа на

1400 автомобилей не будет поставлено 200 автомобилей.

3.2.2 Перевозка автомобилей (предложение превышает спрос)

А вот еще один пример несбалансированной задачи. Давайте предположим, в рамках

модели автомобильной компании, что заказ распределительного центра Денвера

составляет всего 1900 автомобилей. В результате мы получим ситуацию, когда

предложение превышает спрос. В этом случае необходимо ввести фиктивный пункт

назначения, «поглощающий» избыточное предложение. Здесь также можно

назначить нулевую стоимость перевозок в фиктивный пункт назначения, если не

требуется выполнения каких-то особых условий. Например, если необходимо

вывести всю продукцию какого-либо завода, тогда назначается очень высокая

стоимость перевозок oт этого завода до фиктивного пункта назначения.

Новая модель и ее оптимальное решение, полученное с помощью компьютера,

представлены в следующей таблице:

Оптимальное решение показывает, что 400 автомобилей завода Детройта не

востребованы.

Самостоятельная работа

Истинны или ложны следующие утверждения:

Для сбалансированности транспортной модели может понадобиться ввести ка

фиктивные пункты отправления, так и фиктивные пункты назначения.

Объем перевозок в фиктивный пункт назначения равен объему превышения

предложения над спросом.

Объем перевозок из фиктивного пункта отправления равен разности между

спросом и предложением.

В каждом из следующих случаев определите, следует ли ввести фиктивный пункт

отправления или фиктивный пункт назначения, чтобы сбалансировать модель.

Денвер Майами Объем

оизводства

Лос-Анджелес

1000 1000

Детройт

1300 1300

Новый Орлеан

1200 1200

Фиктивн. завод

200 200

Спрос

2300 1400

Денвер Майами Фиктивный

цент

Объем

оизв-ва

Лос-Анджел.

1000 1000

Детройт

900 200 400 1500

Нов. Орлеан

1200 1200

Спрос

1900 1400 400

Ст

. 78 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

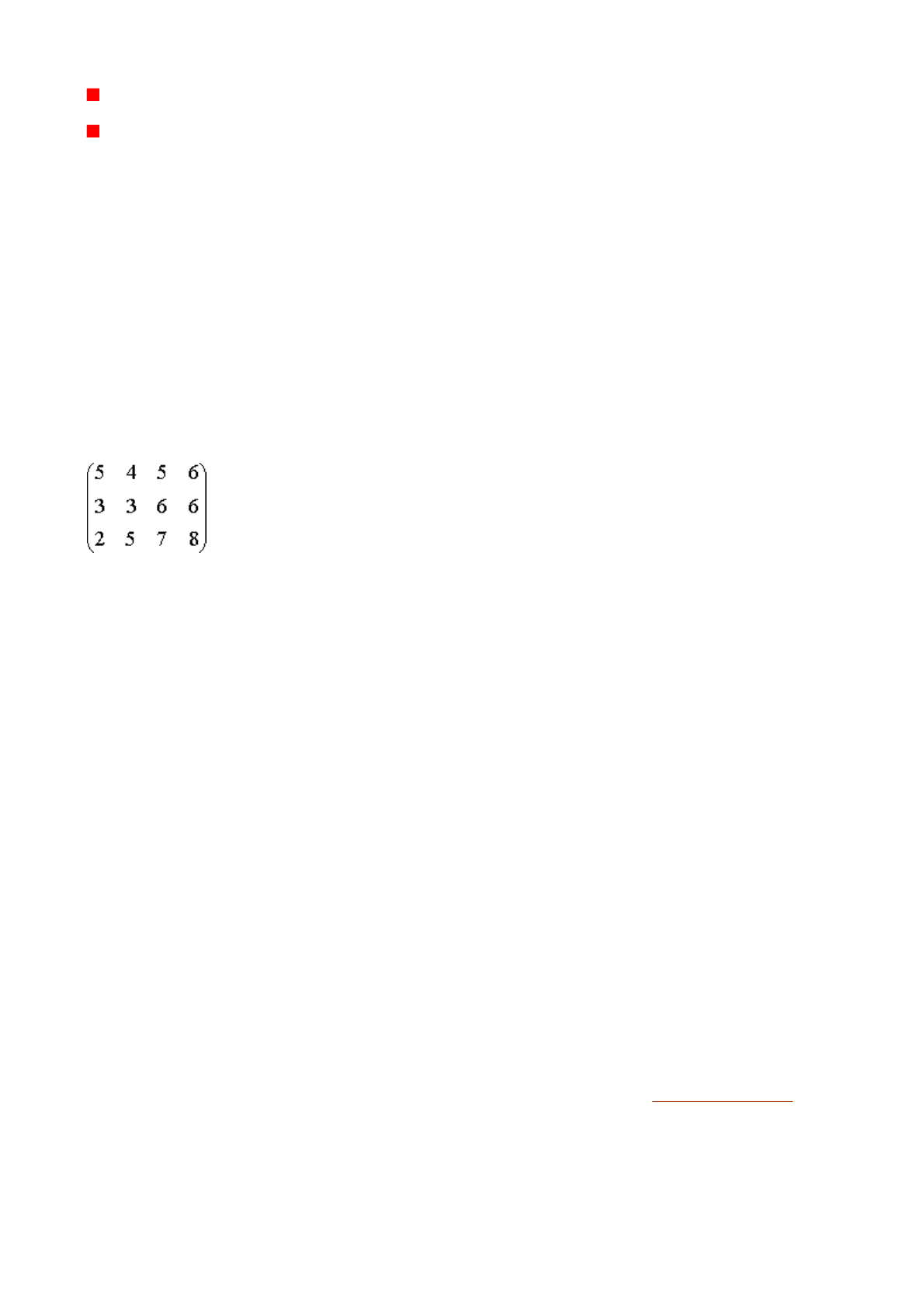
Предложение: а

= 10, а

= 5, a

= 4, a

, = 6. Спрос: b

= 10, b

= 5, b

= 7, b

, = 9.

Предложение: а

= 30, а

= 44. Спрос: b

= 25, b

= 30, b

= 10.

На основе первой таблицы из примера 3.2.1 (здесь введен фиктивный завод)

интерпретируйте решение, где фиктивный завод «поставит» 150 автомобилей

распределительному центру в Денвере и 50 автомобилей распределительному

центру в Майами.

Как в таблице из примера 3.2.2 учесть требование, что завод в Детройте должен

отправить заказчикам все свои автомобили?

3.3. Решение транспортной задачи на компьютере

Рассмотрим следующую задачу. На трех складах оптовой базы имеется однородный

груз в количестве 100, 200 и 400 ед., который необходимо доставить в четыре

магазина в количестве 200, 100, 150 и 250 ед., соответственно. Затраты на перевозку

единицы груза заданы следующей матрицей (номер строки соответствует номеру

склада, а номер столбца — номеру магазина):

Нужно составить такой план перевозок, при котором общие затраты минимальны.

Для начала построим математическую модель этой задачи. Для этого введем

следующие обозначения:

— объем перевозок с i-го склада в j-й магазин;

F — целевая функция (общие издержки).

Математическая модель задачи будет выглядеть следующим образом:

F = 5x

+ 4x

+ 5x

+ 6x

+ 3x

+ 6x

+ 2x

+ 5x

+ 7x

+ 8x

→

min,

≥

0, где i

∈

[1, 3], j

∈

[1, 4].

3.3.1. Решение транспортной задачи с помощью пакетов QSB+ и QS

Воспользуемся программой решения транспортных задач, входящей в пакеты QSB+

и QS. Для ее запуска выберите в меню программ п. 5, если работаете в QSB+, или

п. 6 при работе в QS. Откроется меню функций, аналогичное тому, которое

используется при решении задач линейного программирования (см. раздел 2.4.2).

Задание параметров поиска решения

В меню функций выберите п. 2 — ввод новой задачи. В ответ на запрос программы

введите название решаемой задачи, например

Transportation

Параметры поиска решения данной транспортной задачи задаются на следующей

+ x

= 100,

+ x

= 200,

+ x

= 400,

+ x

= 200,

+ x

= 100,

+ x

= 150,

+ x

= 250,

Ст

. 79 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm

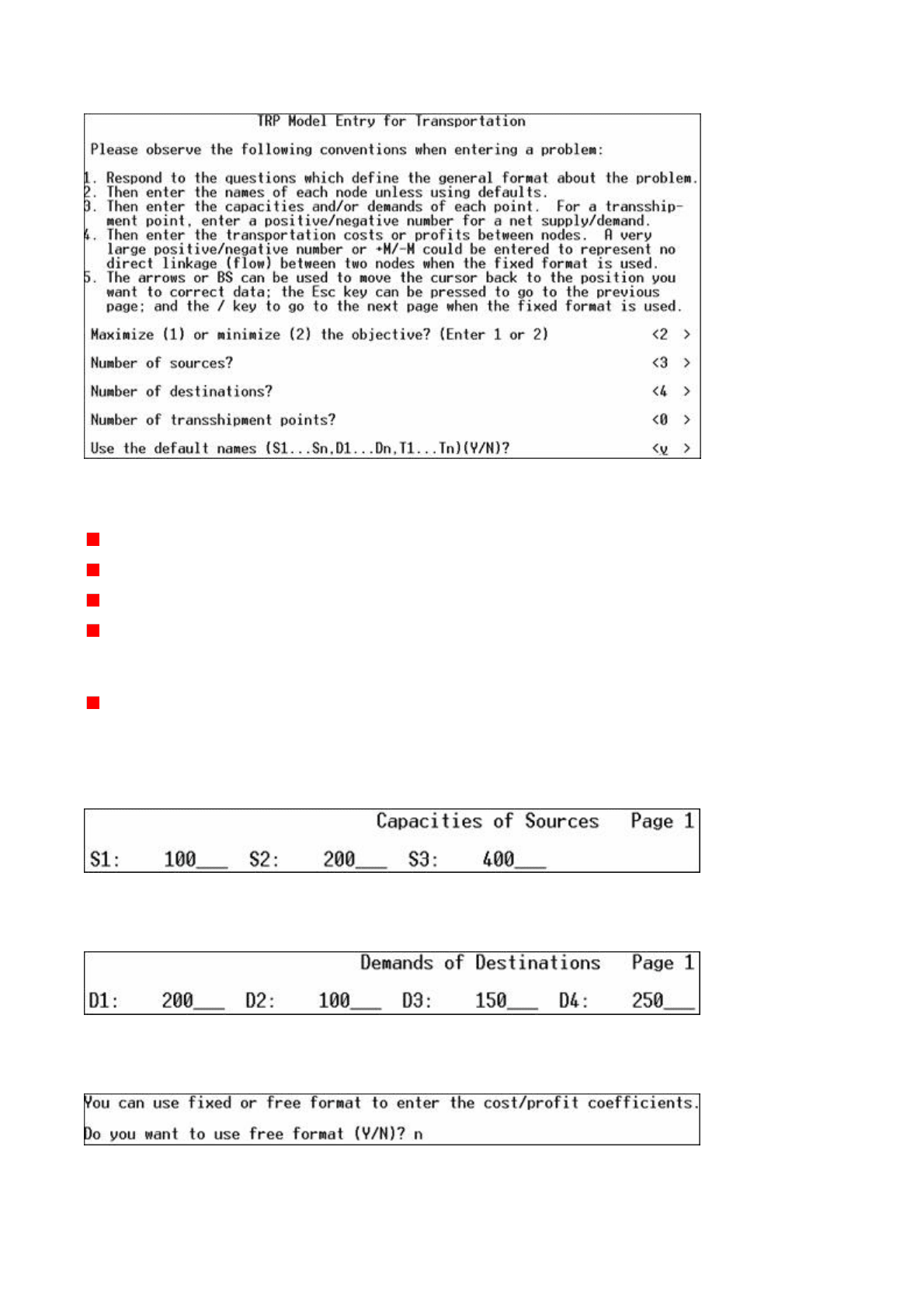
странице:

Вы можете задать (в порядке сверху вниз) следующие параметры (на рисунке они

находятся под списком и начинаются со слова «Maximize»):

максимизировать (

) или минимизировать (

) целевую функцию;

количество пунктов отправления;

количество пунктов назначения;

количество перевалочных пунктов, в которых происходит передача грузов с

одного транспортного средства на другое (

ля стандартных транспортных

задач —

);

использовать стандартные названия пунктов отправления S1…Sn, назначения

D1…Dn и перевалки грузов T1…Tn (

) или задавать другие имена (

Ввод числовых данных

Ввод запасов груза в пунктах отправления осуществляется на следующей странице:

А эта страница предназначена для ввода потребностей в грузе в пунктах назначения:

Далее вам придется ответить на следующий вопрос программы:

Он переводится как «в каком формате вы предпочитаете вводить затраты на

перевозку единицы груза: в свободном (

) или фиксированном (

)?» Ответьте на него.

Ст

. 80 из 101Шаблон для книг

(

Word 97

)

15.09.2004mk:

MSITStore:\\e

b4\New%20files\К

зов.chm::/Manual.htm