Кутузов А.Л. Математические методы и модели исследования операций. Линейная оптимизация с помощью WinQSB и Excel
Подождите немного. Документ загружается.


Заметим, что не случайно, что оптимальное решение расположено в угловой точке
области допустимых решений, где пересекаются две прямые. Если мы изменим
наклон функции z (путем изменения ее коэффициентов), то обнаружим, что в любом
случае решение достигается в одной из угловых точек (или одновременно нескольких
угловых точках). В этом и состоит основная идея построения общего симплексного
алгоритма, который используется при решении задач линейного программирования
на компьютере.
Самостоятельная работа
1.
Для каждого из следующих неравенств определите допустимое полупространство
предполагая, что x
1
, x
2
≥
0.
–3x
1
+x
2
≤7.
x
1
– 2x
2
≥5.
2x
1
– 3x
2
≤ 8.
x
1
– x
2
≤ 0.
–x
1
+ x
2
≥ 0.
2.
Определите направление возрастания целевой функции z в следующих случаях:
Максимизировать z = x
1
– x
2
.
Максимизировать z = –5x
1
– 6x
2
.
Максимизировать z = –x
1
+2x
2
.
Максимизировать z = –3x
1
+ x
2
.
3.
В рамках модели компании, производящей краску, постройте область допустимых
решений и найдите оптимальное решение, учитывая (независимо) следующие
условия:
Ежедневный объем производства краски для наружных работ не должен
превышать 2,5 т.
Ежедневный объем производства краски для внутренних работ должен быть не
менее 2 т.
Ежедневный объем производства краски для внутренних работ должен
превышать ежедневный объем производства краски для наружных работ в
точности на 1 тонну.
Ежедневный расход сырья M1 должен быть не менее 24 т.
Ежедневный расход сырья М1 должен быть не менее 24 т и ежедневный объем
производства краски для внутренних работ должен не менее чем на одну тонну
превышать ежедневный объем производства краски для наружных работ.
4.
Для исходной задачи компании, производящей краску, определите угловые точки
области допустимых решений, где достигается оптимальное решение для
следующих целевых функций:
z = 3x
1
+ x
2
.
z = x
1
+ 3x
2
.
z = 6x
1
+ 4x
2
.
Ст
р
. 21 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

5.
Вернитесь к упражнению 4. Определите, чем решение для третьей целевой
функции отличается от решений для первой и второй целевых функций?
2.2.2. Нахождение минимума целевой функции
Задача о диете
Фирма, производящая пищевую добавку, ежедневно производит ее в количестве не
менее 800 фунтов. Сама пищевая добавка состоит из смеси кукурузной и соевой
муки, состав которых (в фунтах на фунт муки) представлен в следующей таблице:
С точки зрения диетологии необходимо, чтобы в пищевой добавке было не менее
30% белка и не более 5% клетчатки.
Фирма хочет определить рецептуру смеси наименьшей стоимости с учетом
требований диетологов.
Давайте построим математическую модель данной задачи. Прежде всего, определим
переменные этой задачи. Поскольку пищевая добавка состоит только из кукурузной и
соевой муки, то переменными для этой задачи, очевидно, будут:
x
1
— количество (в фунтах) кукурузной муки, используемой в дневном
производстве пищевой добавки;
x
2
— количество (в фунтах) соевой муки, используемой в дневном производстве
пищевой добавки.
Посмотрим, какова же будет целевая функция? В данном случае целевая функция
равна общей стоимости пищевой добавки, производимой за один день
(z = 0.3х
1
+ 0.9х
2
), и должна быть минимальной, то есть
Минимизировать z = 0.3х
1
+ 0.9х
2
.
ПРИМЕЧАНИЕ
Часто встречается и такая запись требования минимизации целевой функции: z = 0,3х
1
+ 0,9х
2
→
min.
Не путайте с теорией пределов математического анализа. Эта запись читается как «Найти минимум
функции z» или «Минимизировать функцию z».
Сформулируем ограничения к модели нашей задачи. Они должны отражать ка
к
производственные требования, так и рекомендации диетологов — с другой.
Итак, с одной стороны, фирма должна выпускать не менее 800 фунтов смеси в день,
значит, соответствующее ограничение можно записать следующим образом:
х
1
+ х
2
≥ 800.
С другой стороны, существует ограничение, связанное с количеством белка и
клетчатки в пищевой добавке Так общее количество белка в смеси, состоящей из х
1
фунтов кукурузной муки и х
2
фунтов соевой муки, равно 0,09x
1
+ 0,6x
2
(фунтов). И это
количество должно составлять не менее 30% от общего объема смеси (x
1
+ x
2
).
Таким образом, получаем следующее неравенство:
0,09x
1
+ 0,6x
2
≥ 0,3(x
1
+ x
2
).
Мука Белок Клетчатка Стоимость
(
в $ за
фу
нт
)
Кукурузная 0,09 0,02 0,30
Соевая 0,60 0,06 0,90
Ст
р
. 22 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
Аналогичным образом строится ограничение для клетчатки:
0,02x
1
+ 0,06x
2
≤ 0,05(x
1
+x
2
).
Сгруппировав в последних двух неравенствах переменные х
1
, и х
2
в правой части
неравенств (для этого их надо просто перенести из правых частей неравенств в
левые), получим:
0,21x
1
– 0,30x
2
≤ 0,
0,03x
1
– 0,01x
2
≥ 0.
Наконец, окончательно математическая модель для нашей задачи примет
следующий вид:
Минимизировать z = 0,3x
1
+ 0,9x
2
при ограничениях
х
1
+ х
2
≥ 800,
0,21х
1
– 0,30х
2
≤ 0,
0,03x
1
– 0,01x
2
≥ 0,
x
1
, x
2
≥ 0.
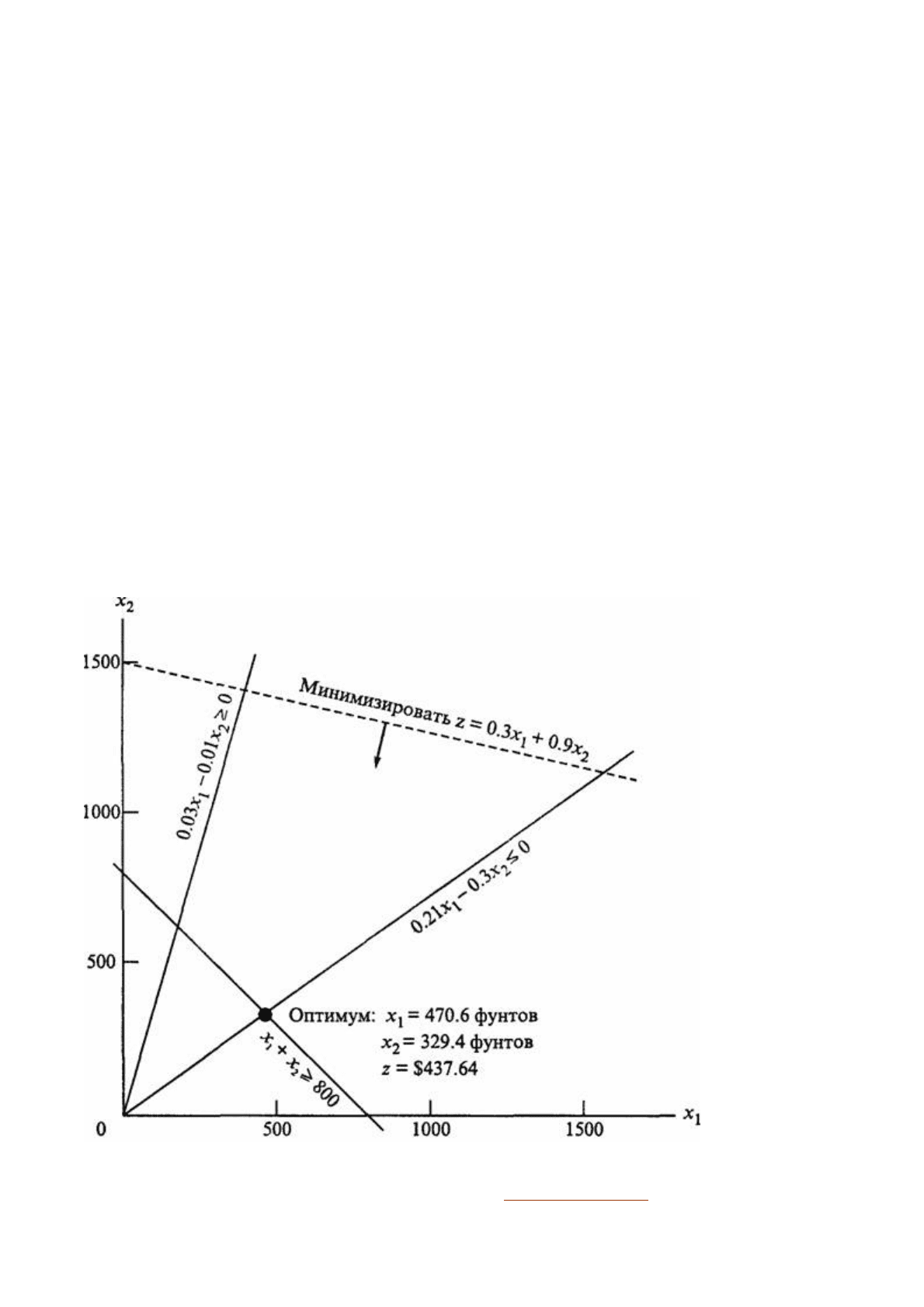
Графическое решение этой задачи представлено на следующем рисунке:
В отличие от задачи о производстве краски (см. раздел 2.2.1), здесь две прямые,
соответствующие неравенствам ограничений, проходят через начальную точку (0, 0).
Ст
р
. 23 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

Для того чтобы провести на графике такую прямую, необходима еще одна точка.
Координаты этой точки можно найти, подставив в уравнение прямой любое значение
для одной переменной и затем из этого уравнения найти значение для другой.
Например, для второго неравенства из системы ограничений положим x
1
= 200, тогда
для второй переменной получаем уравнение 0,21
×
200 – 0,3x
2 =
0, отсюда имеем
x
2
= 140.
Таким образом, прямая 0,21x
1
– 0,30x
2
= 0 проходит через точки (0, 0) и (200, 140).
Как мы уже отмечали ранее, в таком случае для определения допустимой
полуплоскости нельзя использовать в качестве «тестовой» точку (0, 0), здесь следует
взять какую-либо другую, например (100, 0) или (0, 100).
Чтобы найти оптимальное решение в данной модели (а здесь следует
минимизировать целевую функцию), нужно идти в направлении уменьшения ее
значений (это направление на рисунке показано стрелкой).
Оптимальное решение находится на пересечении следующих прямых:
x
1
+ x
2
=
800 и 0,21x
1
– 0,30x
2
= 0,
откуда получаем
x
1
= 470,59 (фунтов) и x
2
= 329,41 (фунтов).
При этих значениях переменных минимальная стоимость производимой ежедневно
пищевой добавки составит
z = 0,3 × 470,59 + 0,9 × 329,41 = $437.65.
Самостоятельная работа
1.
Определите направление убывания следующих целевых функций:
Минимизировать z = 4x
1
– 2x
2
.
Минимизировать z = –3x
1
+ x
2
.
Минимизировать z = –x
1
– 2x
2
.
2.
В задачу о диете добавлено еще одно ограничение: ежедневный расход
кукурузной муки ограничен 450 фунтами. Постройте теперь новое пространство
допустимых решений и найдите оптимальное решение для этого случая.
3.
Найдите оптимальное решение в задаче о диете при условии, что ежедневное
производство пищевой добавки не должно превышать 800 фунтов. Имеет ли такое
решение смысл?
2.2.3. Дополнительные переменные
Давайте вернемся к примерам, рассмотренным ранее (задаче о производстве краски
и о диете). В обоих примерах использовались неравенства типа «меньше или
равно» (знак ≤) и неравенства типа «больше или равно» (знак ≥). В этих примерах
также предполагалась неотрицательность всех переменных.
В данном разделе мы введем два типа дополнительных неотрицательных
переменных (назовем их остаточными и избыточными), которые связаны с
неравенствами типа «≤» и «≥», соответственно.
ПРИМЕЧАНИЕ
Отметим, что в отечественной математической литературе для этих типов переменных не используются
Ст
р
. 24 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

какие-либо специальные названия — они известны просто как дополнительные переменные. В
неравенствах они различаются тем, что перед остаточной переменной всегда стоит знак «плюс», а
перед избыточной — «минус».
Введем также понятие свободной переменной, которая может принимать ка
к
положительные, так и отрицательные значения (и, конечно, значение 0).
Остаточная переменная
Неравенства типа «≤» обычно можно интерпретировать как ограничения на
использование некоторых ресурсов (представленных в левой части неравенств
переменными модели). В такой интерпретации остаточная переменная показывает
количество неиспользованных ресурсов.
В примере с компанией, производящей краску, неравенство 6x
1
+ 4x
2
≤ 24 связано с
использованием сырья М1. Это неравенство эквивалентно равенству
6x
1
+ 4x
2
+ s
1
= 24, где s
1
≥ 0. Здесь остаточная переменная s
1
(=24 – 6x
1
– 4x
2
) равна
неиспользуемому количеству сырья M1.
Избыточная переменная
Неравенство типа «≥» показывает, что «что-то»
д
олжно быть не меньше
определенной величины. Избыточная переменная определяет превышение
значения левой части неравенства над этой величиной.
Например, в модели «диеты» неравенство x
1
+ x
2
≥ 800 показывает, что суточное
производство пищевой добавки не должно быть меньше 800 фунтов. Математически
это неравенство эквивалентно равенству x
1
+ x
2
– S
1
= 800, где S
1
≥ 0.
Положительное значение избыточной переменной S
1
показывает превышение
суточного производства добавки над минимальным значением в 800 фунтов.
Свободная переменная
В приведенных выше примерах условие неотрицательности переменных является
естественным. Но, конечно, возможны ситуации, когда переменные могут принимать
любые действительные значения. Такая ситуация имеет место в следующем примере
ресторана быстрого обслуживания, торгующего порционными мясными пирогами и
чизбургерами.
На порцию мясного пирога
идет 0,25 фунта мяса, а на чизбургер — только 0,2 фунта.
В начале рабочего дня в ресторане имеется 200 фунтов мяса, можно еще прикупить
мясо в течение дня, но уже с наценкой в 25 центов. Мясо, оставшееся в конце
рабочего дня, предоставляется благотворительной организации. Ресторан имеет
прибыль 20 центов от одной порции мясного пирога и 15 центов — от одного
чизбургера. Кроме того, нужно иметь в виду, что ресторан не может продать в день
более 900 бутербродов.
Какова же должна быть доля каждого из бутербродов (то есть сколько порций
мясного пирога и сколько чизбургеров) в ежедневном производстве ресторана, чтобы
максимизировать его прибыль?
Давайте рассмотрим ограничения в сформулированной задаче. Введем обозначения
:
x
1
— количество порций мясного пирога,
x
2
— количество порций чизбургеров.
Для их производства ресторан может ограничиться 200 фунтами мяса (тогда
получаем ограничение 0,25x
1
+ 0,2x
2
≤ 200) или может прикупить еще (в этом случае
Ст
р
. 25 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

получаем ограничение 0,25x
1
+ 0,2x
2
≥ 200). Естественно, выбор одного из этих
неравенств будет существенно влиять на возможное оптимальное решение. Так ка
к
мы не знаем, какое из них необходимо, логично заменить их одним равенством
0,25x
1
+ 0,2x
2
+ x
3
= 200, где x
3
— свободная переменная. Фактически свободная
переменная х
3
в данной ситуации одновременно играет роли как остаточной, так и
избыточной переменных.
Теперь построим целевую функцию. Ресторан хочет максимизировать свою прибыль.
Очевидно, что для максимизации прибыли желательно как можно больше продавать
своей продукции, но для этого необходимы дополнительные закупки мяса. В этом
случае переменная х
3
должна быть отрицательной, то есть должна играть роль
избыточной переменной.
Для того чтобы раскрыть «двойственную» природу переменной х
3
, используем
стандартный математический прием, а именно представим ее в следующем виде.
x
3
= x
3
+
– x
3
–
, где x
3
+
, x
3
–
≥ 0.
Если x
3
+
> 0 и x
3
–
= 0, тогда переменная х
3
играет роль остаточной.
Если, напротив, x
3
–
> 0 и x
3
+
= 0, тогда переменная х
3
выступает в роли избыточной.
Теперь ограничение можно записать в виде равенства
0,25x
1
+ 0,2x
2
+ x
3
+
– x
3
–
= 200.
Целевая функция получает следующее выражение:
Максимизировать z = 0,20 + 0,15x
2
– 0,25x
3
.
Геометрический смысл дополнительных переменных
В предыдущих разделах мы установили, что оптимальное решение задачи линейного
программирования достигается, по крайней мере, в одной вершине области
допустимых решений. Эта точка находится на пересечении, по крайней мере,
д
вух
прямых. Например, в примере из раздела 2.3.1 оптимальное решение находится в
вершине C, которая является пересечением прямых
6x
1
+ 4x
2
= 24 и x
1
+ 2x
2
= 6.
Рассмотрим теперь исходные ограничения:
6x
1
+ 4x
2
≤ 24 и x
1
+ 2x
2
≤ 6
и введем две дополнительные переменные s
1
и s
2
(в данном случае — остаточные).
Теперь мы имеем:
6x
1
+ 4x
2
+ s
1
= 24,
x
1
+ 2x
2
+ s
2
= 6,
где s
1
≥ 0 и s
2
≥ 0
Оказывается, что в вершине C обе дополнительные переменные обращаются в нуль.
Легко проверить, что в любой вершине области допустимых решений, по крайней
мере, две какие-нибудь переменные (дополнительные или основные) всегда
обращаются в нуль (убедитесь в этом сами по рисункам к разделам 2.2.1 и 2.2.2).
Таким образом, чтобы найти координаты всех вершин области допустимых решений,
можно сделать следующее:
Ст
р
. 26 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm

1.
Добавить дополнительные переменные ко всем ограничениям-неравенствам
(пусть количество таких ограничений у нас равно m). При этом система
ограничений превратится в систему линейных уравнений, количество переменных
в которой равно m + 2 (2 основные переменные и m дополнительных — по одной
для каждого ограничения).
2.
Приравнять две любые переменные к нулю.
3.
Решить систему m уравнений с m неизвестными для нахождения координат одной
из вершин области допустимых решений.
Выбирая среди основных и дополнительных переменных разные пары и приравнивая
их к нулю, легко найти координаты всех вершин области допустимых решений.
Аналогичный прием применяется и в симплекс-методе, который используется при
поиске оптимального решения задачи линейного программирования в общем случае,
когда количество основных переменных больше двух.
Самостоятельная работа
1.
В модели компании, производящей краску, рассмотрите допустимое решение
x
1
= 3 т и x
2
= 1 т. Для этого решения найдите недоиспользование сырья M1 и М2.
2.
В модели «диеты» определите превышение над минимальным допустимым
объемом производства пищевой добавки, на которую расходуется 500 фунтов
кукурузной муки и 600 фунтов — соевой.
2.2.4. Основные положения симплекс-метода
В результате графического решения задачи линейного программирования можно
сделать исключительно важный вывод: оптимальное решение достигается в вершине
области допустимых решений, а координаты этой вершины дают нам оптимальные
значения переменных.
На этом выводе основан аналитический метод решения задач линейного
программирования, который заключается в следующем:
Находят вершины области допустимых решений, как это было описано в
предыдущем разделе.
Определяют последовательно значения целевой функции в вершинах.
Вершина, в которой целевая функция приобретает оптимальное (максимальное
или минимальное),значение, является оптимальной вершиной.
Координаты этой вершины и являются искомыми оптимальными значениями
переменных.
Эти правила, сформулированные на основании графического решения задачи на
плоскости, то есть в двухмерном пространстве, справедливы и для трехмерного
пространства. Только в этом случае область допустимых решений будет
представлять собой многогранник. Причем, координаты каждой его вершины будут
представлять собой допустимые решения.
Координаты той вершины, в которой целевая функция имеет максимальное (или
минимальное) значение, являются оптимальным решение задачи. Для трехмерного
пространства, где число переменных равно трем, это нетрудно себе представить. В
практических же задачах, где число переменных может исчисляться десятками и
даже сотнями, никакое самое гениальное пространственное воображение уже не
поможет.
В реальных задачах вершин области
допустимых решений может оказаться
настолько много, что с их полным перебором не справятся и самые мощные из
Ст
р
. 27 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
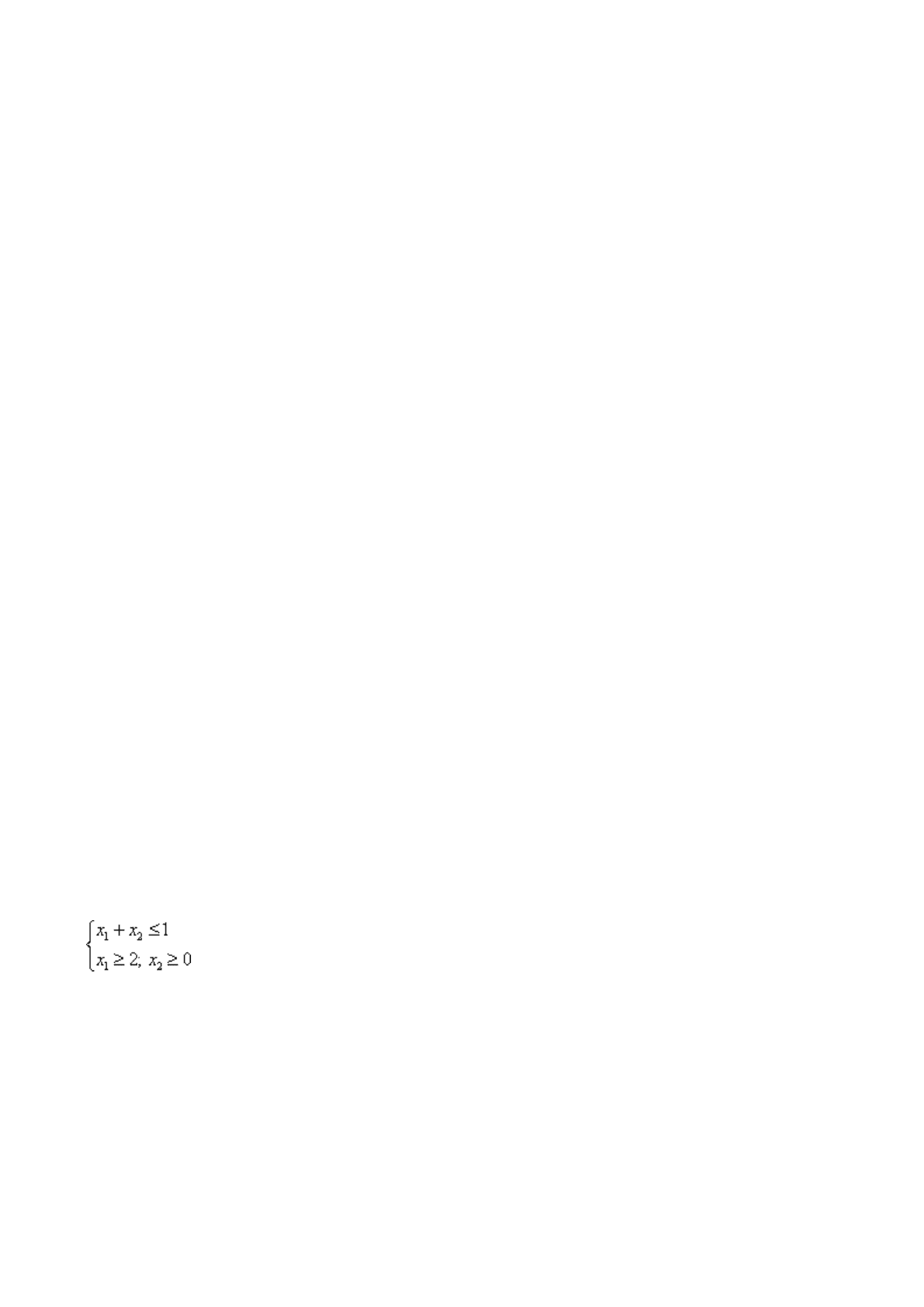
существующих вычислительных машин. Поэтому для аналитического решения задач
линейного программирования разработан специальный алгоритм сокращенного,
направленного перебора вершин. Этот алгоритм обеспечивает переход от одной
вершины к другой в таком направлении, при котором значение целевой функции от
вершины к вершине улучшается.
В геометрии есть такое понятие симплекс. Симплексом тела в k-мерном
пространстве называют совокупность k+1 его вершин. Так, для плоскости при k = 2
симплексом будут три вершины треугольника, при k = 3 — четыре вершины
четырехгранника и т. д. С учетом этого понятия аналитический метод решения
задачи линейного программирования называют симплекс-методом. Вычисления,
обеспечивающие определение значения целевой функции и переменных в одной
вершине, называются итерацией.
Переход от одной вершины к другой производится по достаточно сложному
алгоритму симплекс-метода, который заключается в обмене переменных. Каждый
переход от одной вершины к другой состоит в том, что одна переменная
приравнивается к нулю, а другая переменная, значение которой было равно нулю,
принимает ненулевое значение. На каждой итерации проверяют специальные
признаки, дает ли очередная вершина допустимое и оптимальное решение. Такая
процедура продолжается до тех пор, пока не будут удовлетворены оба признака.
Нужно отметить, что, аналитическое решение задачи линейного программирования
— дело весьма сложное, поэтому более подробно описывать его не будем. И
действительно, чтобы смотреть телевизор, совсем необязательно иметь
представление о принципах его работы. Точно так же, чтобы принимать оптимальное
решение на основе математической модели, совсем необязательно знать достаточно
сложные алгоритмы, по которым это решение находится. Однако когда известно,
каким путем получен результат, все-таки больше уверенности в его правильности.
Поэтому особо любознательным советуем прочесть [7, 10, 14, 19].
В заключение отметим, что симплекс-метод используется во всех программах,
предназначенных для решения задач линейного программирования, в частности,
программе Excel и пакетах прикладных программ QSB+ и QS.
2.2.5. Если решения нет
При решении задач линейного программирования достаточно часто оптимального
решения получить не удается. Это происходит по двум причинам, которые мы сейчас
и рассмотрим.
Итак, первую причину проиллюстрируем на следующем примере. Рассмотрим
следующую систему:
.
Теперь давайте представим ее графически.
Ст
р
. 28 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
На нашем рисунке видно, что нет таких значений x
1
и x
2
, которые удовлетворяли бы
системе. Значит, в данном случае область допустимых решений отсутствует. Про
такую систему говорят, что ограничения несовместны.
К сожалению, это часто встречается на практике, а не только теоретически
возможный вариант. В таких случаях Excel, например, будет выдавать
соответствующее сообщение.
В общем случае несовместимость может быть следствием двух причин:
неправильная математическая модель;
неправильные исходные данные.
Вторую причину невозможности получить оптимальное решение также рассмотрим
на примере максимизации целевой функции z = x
1
при следующей системе
ограничений:
Изобразим решение графически.
Ст
р
. 29 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
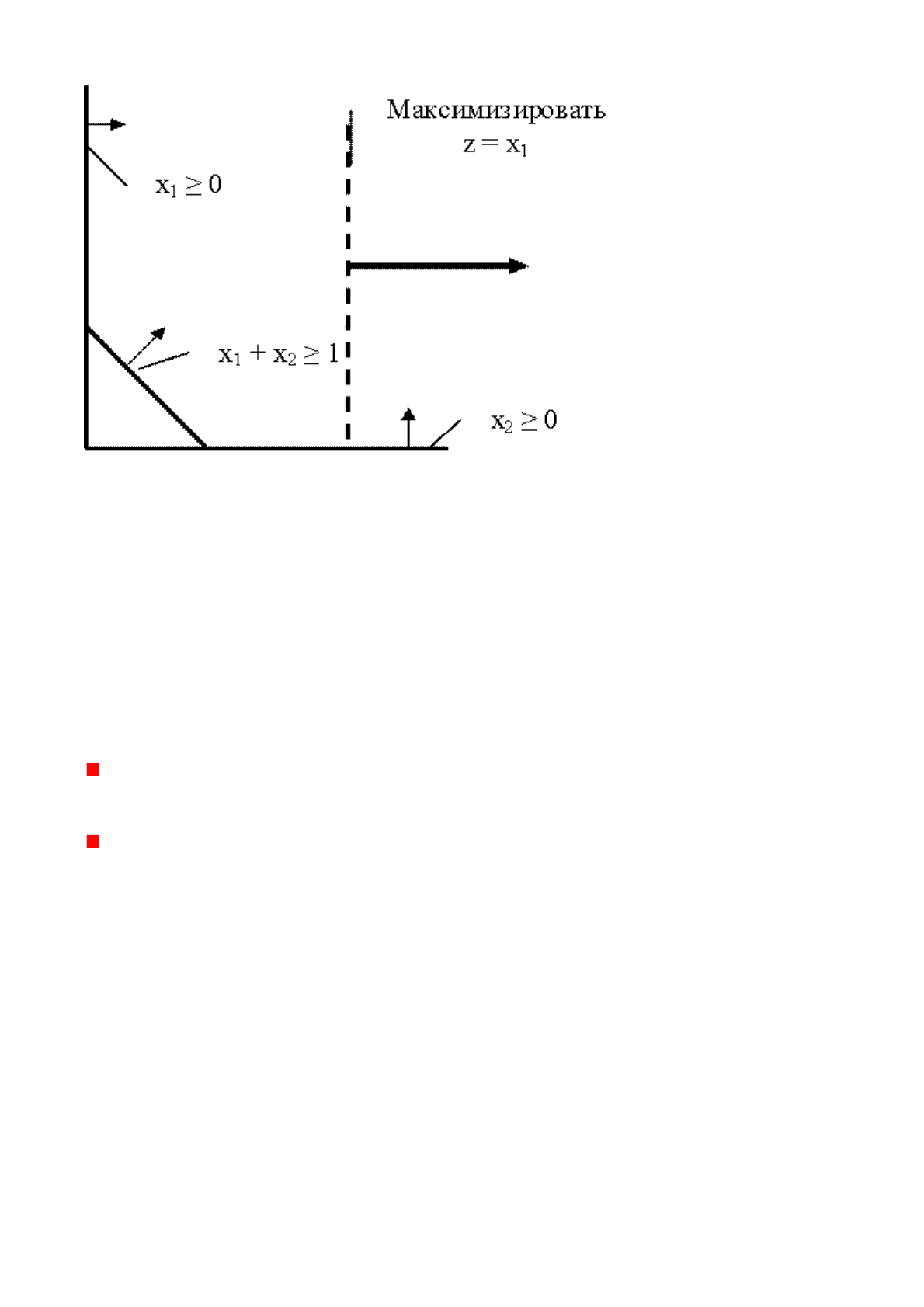
На нашем рисунке видно, что область допустимых решений не ограничена сверху. В
таком случае при максимизации целевой функции z = x
1
решение получено быть не
может, так как целевая функция, как и область допустимых значений, не ограничена
сверху. При решении такой задачи на компьютере, например, с использованием
Excel, будет выдано соответствующее сообщение.
Неограниченность целевой функции — это, как правило, следствие ошибки в
математической модели. В реальности не встречаются случаи, когда целевая
функции (например, прибыль или издержки) была бы бесконечно большой или
бесконечно малой. Поэтому если такой результат вытекает из вашей модели, это
наверняка означает, что вы не учли каких-то существенных ограничений. Чтобы
избежать этого, нужно придерживаться следующих правил:
при максимизации целевой функции она должна быть с помощью ограничений
ограничена сверху (то есть в модели должно быть достаточное количество
ограничений типа «≤»);
аналогично, при минимизации целевой функции она должна быть с помощью
ограничений ограничена снизу (то есть в модели должно быть достаточное
количество ограничений типа «≥»).
2.3. Графический анализ чувствительности
Поскольку модель линейного программирования является всего лишь
«моментальным снимком» реальной ситуации, когда параметры модели
(коэффициенты целевой функции и неравенств ограничений) фиксированы, было бы
естественным изучить влияние изменения параметров модели на полученное
оптимальное решение задачи линейного программирования. Такое исследование
называется анализом чувствительности.
Как мы уже отмечали ранее, анализ чувствительности полученного решения
позволяет получить дополнительную информацию о поведении оптимального
решения при изменении некоторых параметров модели.
Нами уже подчеркивалось, что это особенно важно в тех случаях, когда невозможно
точно оценить параметры модели. В таких случаях следует изучить поведение
оптимального решения в окрестности первоначальных оценок значений параметров
Ст
р
. 30 из 101Шаблон для книг
(
Word 97
)
15.09.2004mk:
@
MSITStore:\\e
p
b4\New%20files\К
у
т
у
зов.chm::/Manual.htm
