Кульков С.Н., Буякова С.П. Современные методы структурного анализа в материаловедении
Подождите немного. Документ загружается.

31
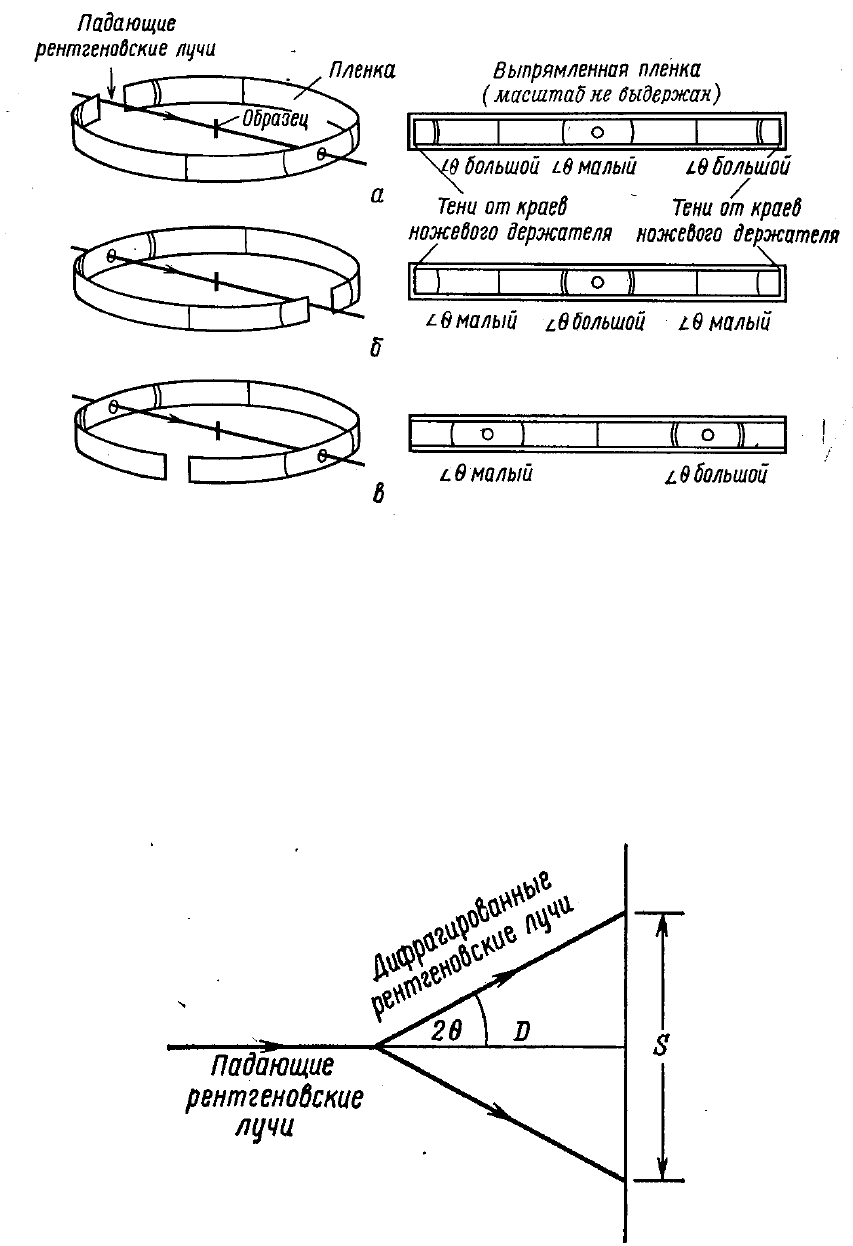
Рис. 20. Схема рентгеновской камеры
Существуют два способа регистрации – на плоскую и цилиндриче-
скую пленку.
Плоская пленка
tg2Θ = S/2D для Θ < 30° и tg(180 – 2Θ) = S/2D для Θ > 60°.
Этот интервал углов используется для точного определения перио-
дов решеток и их изменения, рис. 21.
Рис. 21. Способ регистрации – плоская пленка

32
Цилиндрическая пленка
Пересечение дифракционных конусов с цилиндрической пленкой
происходит по кривым 4-го порядка, рис. 22.
Съемка – симметричная, асимметричная. Для симметричного рас-
положения пленки необходима калибровка рентгеновской камеры, для
асимметричной съемки из одной рентгенограммы можно определить
R
эфф
– истинный радиус рентгеновской камеры:
2
π
R
эфф
= A + B,
где A и B – расстояния между одноименными отражениями внутри и
снаружи пучка на пленке.
Дифракционный угол (в радианах) равен
Θ = S/4R
эфф
, (41)
где S – длина дуги на пленке между одноименными отражениями.
Необходимо учитывать поправку на поглощение в образце, кото-
рый может быть абсолютно прозрачным, полупрозрачным и абсолютно
непрозрачным.
В этом случае для S необходимо вносить поправку:
2S
испр
= 2S
измер
– 2rcos
2
Θ, (42)
где r – радиус цилиндрического образца.
Регистрация дифрактометром
Наиболее распространена съемка по методу Брэгга–Брентано,
рис. 22.
Плоский образец помещается на ось вращения гониометра. Проек-
ция фокуса F и детектор D расположены на одной окружности R. Фоку-
сировка приблизительная – надо чтобы образец был изогнут по фокуси-
рующей окружности. При этом дефокусировка тем меньше, чем меньше
расходимость пучка.
Особенность метода
: в отражающем находятся положении только
те кристаллы (плоскости hkl), которые параллельны поверхности образ-
ца.
Приготовление образцов в методе порошка
: как правило, это «стол-
бик» диаметром 0,2…1,0 мм для чего исследуемый материал с размером
зерна порядка 10
–2
мм, который помещается в капилляр, либо склеива-
ется столбик из порошка, или образец берется в виде проволочки. Для
съемки дифрактометром обычно берется плоский образец и ограничи-
вается расходимость рентгеновского пучка.

33
Рис. 22. Схема съемки при регистрации дифрактометром
Точность определения межплоскостных расстояний d
: (не точнее,
чем
λ
).
Продифференцируем формулу Вульфа–Брэгга
λ
= 2dsinΘ по d и Θ
0 = 2ΔdsinΘ + 2dcosΘΔΘ
или
Δd/d = – ctgΘΔΘ.
Аналогично получаем
ΔΘ = Δ
λ
/
λ
tgΘ или Δ
λ
/
λ
= ΔΘ/tgΘ. (43)
Метод порошков дает обычно точность 0,1 %. Существует потреб-
ность определения с большей точностью. Поскольку длина волны
обычно известна с точностью 0,002 %, а CuK
α
и FeK
α
около 0,005 %, то
можно определить d по крайней мере с этой точностью.
Высокой точности можно достичь применением прецизионных ме-
тодов съемки и обработки, т. е. при одной и той же погрешности опре-
деления угла ΔΘ погрешность уменьшается с ростом угла как ctgΘ. Об-
ласть углов больше 60°
называется прецизионной.
Существует три типа погрешностей
:
1) определение положения линий на рентгенограмме;
2) неточная геометрия съемки;
3) физические факторы.
(1 – случайные; 2, 3 – систематические).

34
Учет ошибок
Анализ определения точности определения d показывает, что прак-
тически все ошибки стремятся к «0» при Θ ⇒ 90°, рис. 23. Однако экс-
периментально измерить такие углы невозможно, поэтому используют
так называемую экстраполяцию параметров на угол, равный 90°. В ос-
новном по двум видам аппроксимирующих функций:
• по cos
2
Θ;
• по
22
1cos cos
2sin
⎛⎞
Θ
Θ
+
⎜⎟
ΘΘ
⎝⎠
.
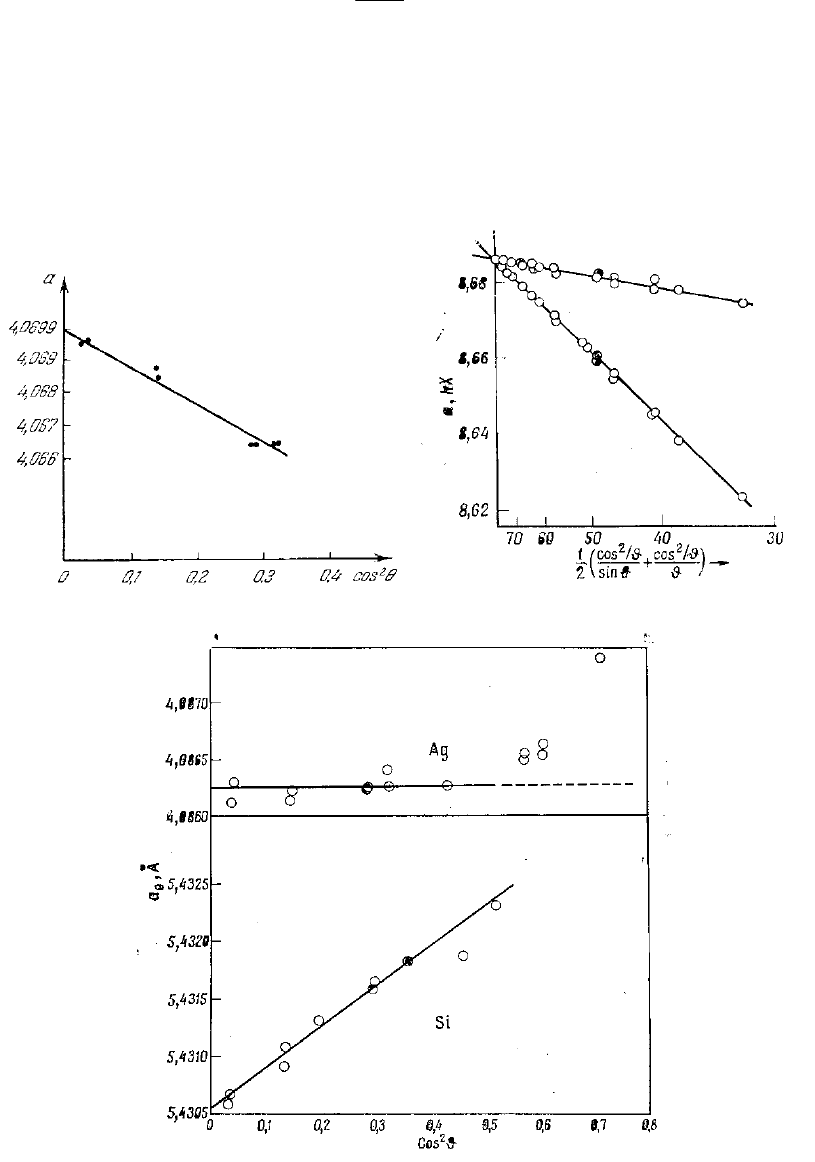
Графически это представлено на рис. 18, причем видно, что экстра-
поляционные функции практически линейные.
Учет различных ошибок может быть осуществлен по следующим
формулам:
1. Поглощение в образце: ΔΘ =
R
μ
4
2sin
Θ
.
2. Смещение плоскости образца от пучка: ΔΘ =
R
s Θcos
.
3. Преломление в образце: a
испр
= a
изм
(1 +
δ
).
4. Отклонение плоскости от фокуса: ΔΘ = –
γ
2
ctg/12.
5. Проникновение лучей в образец: Δd/d = sin2ΘctgΘ.
6. Неточная установка нуля гониометра: Δd/d = ctgΘ.
Индицирование порошковых рентгенограмм
Ячейка известна
Нужно:
• определить все углы дифракции;
• вычислить углы для всех разрешенных в данной структуре (hkl);
• сопоставить полученные данные и определить (hkl) для полученной
рентгенограммы.
Ячейка неизвестна
Индицирование в этом начинают в предположении наивысшей
симметрии ячейки, т. е. с кубической системы. Анализ структурного
фактора для кубических структур показывает, что для этих структур
возможен только определенный набор отражений. Поэтому из квадра-
тичной формы получаем, что, если разделить экспериментально изме-
ренные значения sin
2
(Θ
hkl
) на некоторое число, наибольший общий де-
литель, равный
λ
2
/4a
2
, то в остатке получаем набор целых чисел, опре-
деляемый суммой квадратов индексов (hkl):
35
sin
2
(Θ) =
2
2
4a
λ
(h
2
+ k
2
+ l
2
). (44)
В соответствии со структурным фактором возможны только сле-
дующие наборы сумм квадратов целых чисел:
• ПК: 1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 16...
• ОЦК: 2, 4, 6, 8, 10, 12...
• ГЦК: 3, 4, 8, 11, 12, 16...
Рис. 23. Графики для точного определения а и d
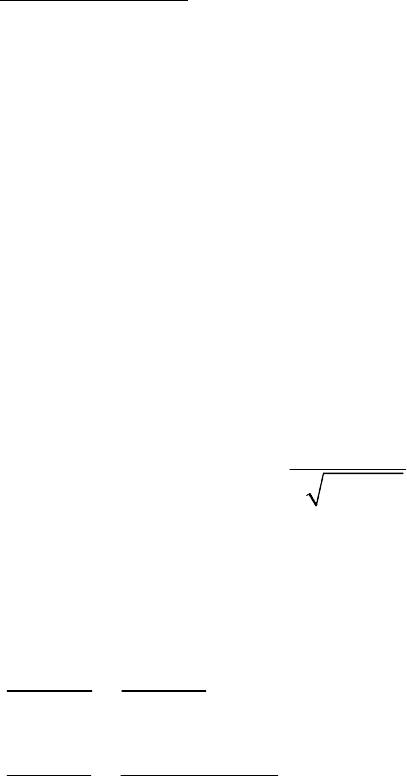
36
Как правило, из эксперимента получаем близкие к целым значени-
ям для Р, I, F-решеток числа. По наибольшему общему делителю (НОД)
находим параметр «а», а затем уточняем для дальних линий.
Общее правило
: низкие порядки существенны для правильного, но
приближенного определения размеров ячейки и ее типа, а более высо-
кие – для уточнения расчетов.
Пример: для длины волны CoK
α
= 1,7902 А получен набор углов
2Θ. Расчет sin
2
Θ дает:
0,0343; 0,0919; 0,1258; 0,1370; 0,1839; 0,2752; 0,3097 и т. д.
НОД первых двух чисел равен 0,0115, делим все остальные на этот
НОД и получаем:
2,98; 7,99; 10,94; 11,91; 15,99; 23,93; 26,93...
Как видно, этот набор очень близок к набору для гранецентриро-
ванного куба: 3, 8, 11, 12, 16, 24 и т. д., откуда делаем вывод, что рент-
генограмма принадлежит веществу с ГЦК решеткой.
Его параметр равен
1,7902
8, 34 A.
2 0, 0115
a ==
Если провести индицирование в предположении кубической сим-
метрии не удается, то его проводят в предположении тетрагональной
или гексагональной симметрии.
Для l = 0 получаем:
•
2
1
2
1
2
2
2
2
1
2
2
2
sin
sin
kh
kh
+
+
=
Θ
Θ
– для тетрагональной решетки и
•
11
2
1
2
1
22
2
2
2
2
1
2
2
2
sin
sin
hkkh
khkh
++
++
=
Θ
Θ
– для гексагональной решетки.
Тогда для части линий на рентгенограммах их квадраты синусов
относятся друг к другу как целые числа:
• 1, 2, 4, 5, 9, 10, 11, 13 (ГЦТ);
• 1, 3, 4, 7, 9, 12, 13, 16 (ГПУ).
Графическое индицирование
Для кубических кристаллов можно записать
a = d√(h
2
+ k
2
+ l
2
). (45)
Таким образом, можно построить график (рис. 24), по которому от-
кладывая в масштабе оси d измеренные значения межплоскостных рас-
стояний, совмещаем на специальной приготовленной линейке все зна-
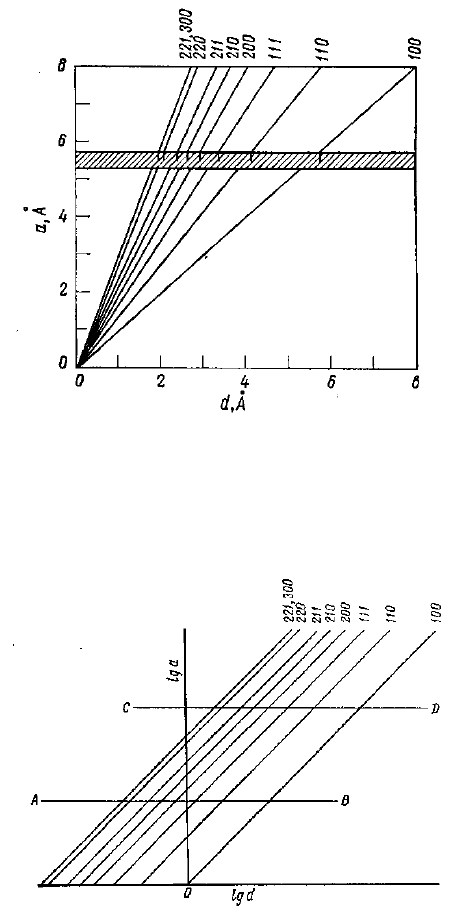
37
чения с линиями на номограмме и ищем максимальное совпадение всех
линий. Если это удается, то по оси ординат считываем значения пара-
метра решетки, рис. 24.
Рис. 24. Пример графического индицирования
рентгенограммы кубического кристалла
Аналогичную номограмму можно построить в логарифмических
координатах, рис. 25.
Рис. 25. Номограмма в логарифмических координатах
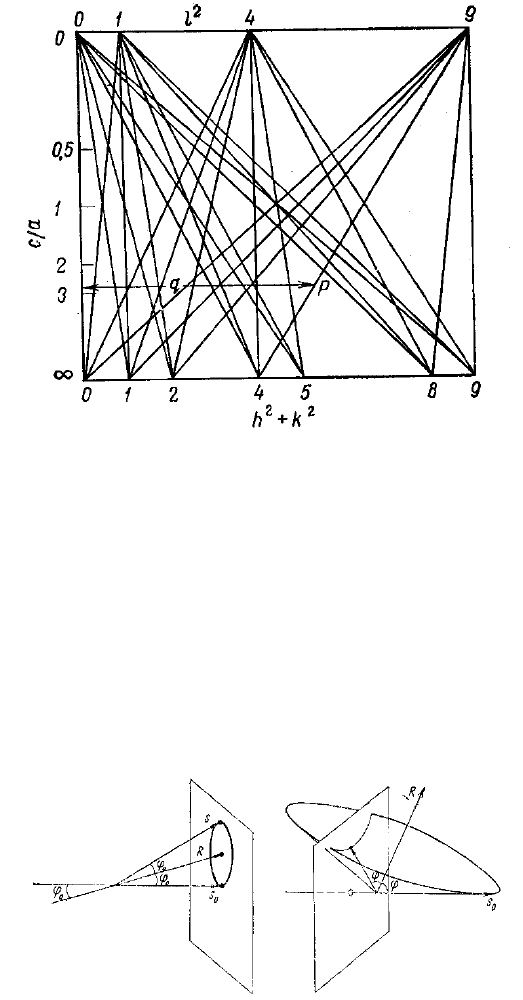
Для графического индицирования тетрагональной и гексагональной
структур строится график с/а = f(d) (график Хэлла–Дэви), для которого
разность lgd зависит только от индексов и соотношения с/а.
Возможно построение номограммы Бьерстрема, рис. 26.
38
Рис. 26. Номограмма Бьерстрема
Метод Лауэ
Метод Лауэ находит применение на самом первом этапе изучения
атомной структуры кристаллов, рис. 27. С его помощью определяют
кристаллический класс с точностью до центра инверсии. Дифракцион-
ная картина получается от неподвижного монокристалла при облучении
его непрерывным рентгеновским спектром. Образец – монокристалл,
либо одно крупное зерно поликристаллического образца.
Рис. 27. Геометрия интерференционной картины
Прямая съемка – получение лауэграммы, лауэграммы получаются
для тонких или прозрачных для рентгеновских образцов. Если образец
непрозрачен, то применяют метод обратной съемки, получают эпи-
граммы, рис. 28. В этом случае камера имеет несколько другой вид для
получения обратно отраженных лучей.
В методе Лауэ все лучи, отраженные от одной и той же кристалло-
графической плоскости, но разного порядка, будут совпадать по на-
правлению и в одном и том же направлении будут распространяться
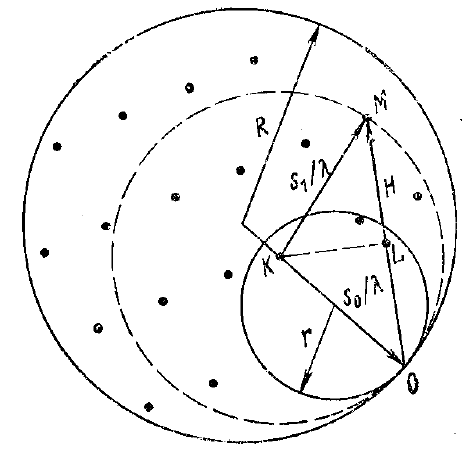
39
волны с длинами
λ
,
λ
/2,
λ
/3 и т. д. Поэтому метод Лауэ нельзя использо-
вать, если требуется измерение интенсивности только в одном порядке
отражения.
Рис. 28. Формирование интерференционной картины в методе Лауэ
Пятна располагаются по зональным кривым, соответствующим
кристаллической зоне. (Кристаллическая зона – совокупности плоско-
стей, параллельных одному направлению – оси зоны [UVW]).
Формула для расчета:
tg2Θ = l/D, (46)
где l – расстояние пятна от изолированного пучка; D – расстояние «об-
разец–пленка».
Применение метода
1. Определение качества кристаллов. Определяют по форме пятен.
Хороший кристалл дает четкие пятна. Сросшиеся кристаллы дают рас-
щепляющиеся на несколько (в соответствии с числом кристаллитов)
близко расположенных пятен. Деформированные кристаллы – пятна
вытянутся (в радиальном направлении) – появляется так называемый
рентгеновский астеризм.
2. Определение ориентировки не ограненных кристаллов (через по-
строение проекций).
3. Определение
симметрии кристаллов. В этом случае кристаллы
ориентируют, чтобы первичный луч был параллелен плоскости или оси
симметрии.

40
Так как лучи полихроматичны, то кристаллы с подобными ячейка-
ми и структурами, но с различными параметрами, порождают одинако-
вые рентгенограммы (лауэграммы). В этом смысле метод Лауэ обратен
методу порошка, т. к. дает только относительное расположение различ-
ных плоскостей решетки, но не позволяет рассчитать межплоскостные
расстояния. Поэтому он используется в основном для
определения сим-
метрии кристалла.
Метод вращения монокристалла
Этот метод основной при определении атомной структуры кри-
сталлов. Определяют размеры элементарной ячейки, число атомов, при-
ходящихся на одну ячейку.
Дифракционная картина получается от монокристалла, вращающе-
гося вокруг определенного кристаллографического направления при
облучении монохроматическим или характеристическим излучением.
Юстировка кристалла производится либо по огранке, либо методом
Лауэ; устанавливают, чтобы, например, направление [100] было
вдоль
оси вращения.
Дифракционные максимумы располагаются вдоль параллельных
прямых – слоевых линий – симметрично относительно вертикали, про-
ходящей через первичное пятно, рис. 29.
Рис. 29. Геометрия интерференционной картины
при вращении монокристалла
