Кульков С.Н., Буякова С.П. Современные методы структурного анализа в материаловедении

Подождите немного. Документ загружается.

= – 2

(uh + vk + wl). (22)

То есть в том случае, когда атом М, наряду с атомом О, расположен

в узле кристаллической решетки (а значит uvw – целые числа), необхо-

димое и достаточное условие того, чтобы разность фаз

была кратной

– индексы (hkl) должны быть целыми.

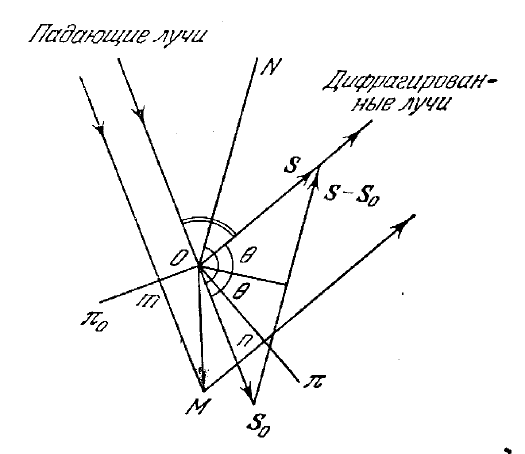
Рис. 12. Изображение двух произвольно расположенных

в пространстве атомов О и М

Другими словами дифрагированный луч возникает тогда и только

тогда, когда вектор рассеяния (S – S

равен вектору обратной решетки.

Поскольку S и S

единичные векторы, то ⏐S – S

⏐= 2sinΘ.

Значит,

2sinΘ/

= s = R

hkl

= 1/d

hkl

, (23)

т. е. получили формулу Вульфа–Брэгга.

Построение Эвальда. (Сфера Эвальда).

Геометрическая интерпретация дифракции

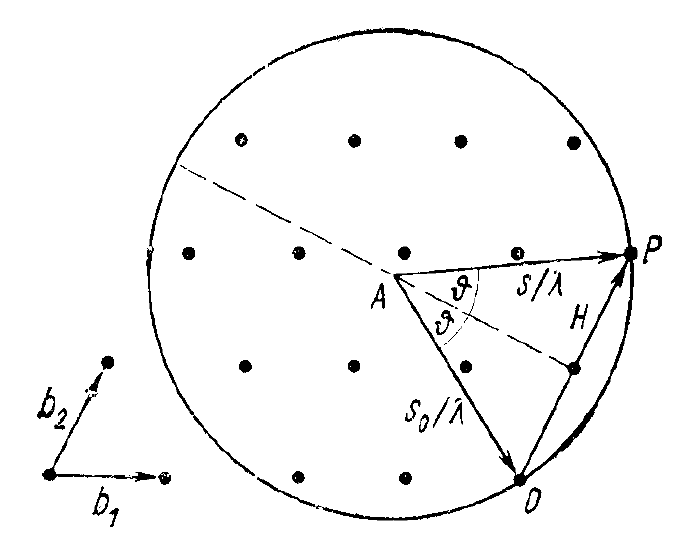
Нарисуем в обратном пространстве сферу радиусом 1/

, рис. 13.

О – точка, начало обратной решетки, вокруг которой может поворачи-

ваться обратная решетка, а значит, и кристалл.

Дифрагированные лучи возникают лишь тогда, когда точка Р, на-

ходящаяся на сфере, совпадет с узлом обратной решетки. В этом и толь-

ко в этом случае вектор рассеяния ОР будет совпадать с вектором об-

ратной решетки. В случайном положении на сфере отражения может не

оказаться ни одного узла обратной решетки, а значит, отраженного от

кристалла луча не будет.

Рис. 13. Сфера Эвальда и обратная решетка кристалла

1.5. Множители интенсивности

Все, что было рассмотрено до сих пор – это вопросы дифракции,

однако интерференция лучей учитывалась чисто качественно.

Перейдем к учету и рассмотрению интенсивностей дифрагированных

лучей.

При выводе условий усиления лучей, идущих от системы парал-

лельных плоскостей (условие Вульфа–Брэгга), предполагалось, что:

• падающие лучи параллельны и монохроматичны;

• решетка

примитивная;

• электроны, рассеивающие рентгеновское излучение – в точке;

• атомы кристалла неподвижны (нет теплового движения);

• поглощение в кристалле отсутствует;

• размеры кристалла малы по сравнению с расстоянием до точки на-

блюдения;

• вторичные волны не взаимодействуют с первичными.

Однако ни одно из этих условий на самом деле не отражает реальной

картины взаимодействия рентгеновского излучения с кристаллом.

Рассмотрим решетку с одним атомом в ячейке с рассеивающей

способностью (атомным фактором рассеяния) f.

– падающий пучок; S – рассеянный;

– длина волны.

Определим интенсивность для малого кристалла, полагая, что по-

глощения нет, т. е. на все атомы падает одинаковый поток излучения.

Кристалл ограничен: N

a, N

b, N

c: N – большие числа ≈10

. N

a,b,c

–

количество атомов по граням.

Ранее показано, что разность фаз между волнами, рассеиваемыми

атомами в узлах (000) и (uvw), равна

= – 2

(uh + vk + wl),

где hkl – координата вектора рассеяния, hkl – любые.

Результирующая рассеянная волна есть сумма N

волн с ам-

плитудами fа

, где а

– амплитуда рассеяния одним электроном. Для

атома с координатами (uvw) можно записать:

A = fа

exp(i

uvw

а для суммарной волны:

A = ΣΣΣfа

exp(i

uvw

)

(суммирование идет по трем координатам).

Нас интересует интенсивность этой волны, т. е. I =|A|

I = I

⏐ΣΣΣexp(–2

i(hu + kv + lw))⏐

где I

–

интенсивность волны, рассеянной одним электроном, т. е. а

Или иначе:

I = I

⏐G

hkl

⏐

(24)

где G

hkl

– так называемая интерференционная функция.

Вид G

hkl

вблизи узла, например (000), показан на рис. 14.

Рис. 14. Интерференционная функция

Структурный фактор для кристалла с базисом

Пусть в элементарную ячейку входит n атомов А

, А

,..., А

. Поло-

жение атома А

определяется элементарными векторами а, b, c:

a + y

b +z

где 0 < {x, y, z} < 1, т. к. атомы расположены в пределах элементарной

ячейки.

Обозначим f

...f

–

факторы рассеяния разных атомов в ячейке. Ам-

плитуда волны, рассеиваемой i-атомом,

= f

где а

– амплитуда, рассеяния свободным электроном.

Волна, рассеиваемая от кристалла, есть

A =Nf

(25)

где N – число элементарных ячеек в кристалле.

Разность фаз волн для атома, находящегося в начале координат и

для i-го атома:

= – 2

h + v

k + w

l). (26)

Волна для всего кристалла с учетом n атомов в ячейке:

A = Nа

Σf

exp{–2

h + v

k+ w

l)} = Nа

hkl

, (27)

где F

hkl

– структурный фактор.

Или иначе:

hkl

= Σf

exp{–2

(sx

)},

где s = (S – S

, х

– вектор, соединяющий i-атом с началом ячейки.

Интенсивность дифрагированного пучка квадрату амплитуды, т. е.

hkl

⏐F

hkl

⏐

= F

hkl

= ΣΣf

exp{–2

i[h(x

–x

)+k(y

–y

)+l(z

–z

)]}. (28)

Таким образом, структурный фактор решетки зависит только от

взаимного расположения атомов в решетке.

Вычисление структурного фактора

ГЦК-решетка. В ГЦК решетке четыре атома, координаты

которых: (000), (1/2,1/2,0), (1/2,0,1/2), (0,1/2,1/2).

Подставляем значения {x,y,z} в F

hkl

и расписываем экспоненту как

exp(i

) = cos

+ isin

. (29)

Слагаемые с sin

при любых целых hkl равны 0. Для cos

результат

определяется четностью индексов – если все они четные или все нечет-

ные, то каждый cos

= 1 и F

hkl

= 4f. Если hkl разной четности, то два

cos

= 1, а два cos

= –1, т. е. F = 0.

Таким образом, отражения от плоскостей с индексами разной чет-

ности будут иметь интенсивность, равную нулю, а отражения от плос-

костей с индексами одной четности – 16f

ОЦК-решетка. Координаты атомов: (000) и (1/2,1/2,1/2)

hkl

= f{1 + exp[–

i(h + k + l)]}. (30)

Таким образом, если (h + k + l) = 2n – сумма индексов плоскости

четная, то F = 2f; если же (h + k + l) = 2n + 1 – сумма индексов плоско-

сти нечетная, то F = 0.

Соответственно, интенсивность равна нулю во втором случае

и 4f

– в первом.

Атомный множитель

Интенсивность луча, рассеянного от атома, можно было бы считать

равной А

ат

= Σa

, если бы все электроны располагались в точке. На са-

мом деле атом имеет конечные размеры, сравнимые с длиной волны.

Поэтому волны, рассеянные разными частями электронного облака ато-

ма, будут частично гасить друг друга, т. к. будут отличаться по фазе,

рис. 15. Поэтому А

ат

< Σa

. Таким образом, интенсивность рассеяния в

данном направлении равна произведению некоторого коэффициента f

называемого атомным множителем на интенсивность рассеяния одним

свободным электроном I

I = I

. (31)

Интенсивность рассеяния одним электроном по формуле Томсона

равна

1cos2

⎛⎞

⎜⎟

⎝⎠

, (32)

т. е. интенсивность рассеяния от атома будет

1cos2

IIf

⎛⎞

⎜⎟

⎝⎠

. (33)

Атомная амплитуда зависит от длины волны, порядкового номера

элемента и угла рассеяния, вид этой зависимости показан на рис. 16.

Можно показать, что

sin

() ,

fur dr

∫

(34)

где u(r) = 4

(r);

(r) – вероятность нахождения электрона в объеме

dV, удаленном от центра атома на расстояние r; s =

sinΘ, а

– разность

фаз волн, рассеиваемых объемом dV по отношению к началу координат.

Рис. 15. Рассеяние рентгеновских лучей атомом конечного размера

Рис. 16. Зависимость атомного фактора рассеяния от угла и длины волны

Температурный фактор

В решетке атомы колеблются, т. е. занимают не те места, которые

предписаны в модели идеальной кристаллической решетки.

Обозначим Δх

смещение n-го атома относительно n-узла. В том

случае, когда частота изменения х велика по сравнению со временем

измерения, но мала по сравнению с частотой рентгеновских лучей, то

можно считать, что дифракция происходит на фиксированных совокуп-

ностях атомов, а средняя интенсивность дает интенсивность всех кон-

фигураций.

Структурный фактор в этом случае равен

hkl

= fexp[–2

i(sΔх

)]}. (35)

Ряд преобразований дает для среднего

hkl

> = fexp[1–

Δx

]. (36)

После разложения в ряд амплитуду рассеяния обычно записывают

в виде

hkl

> = fexp(–M), (37)

где

M =

Δx

. (38)

Следовательно, интенсивность равна

D = exp(–2M) = exp(–

sin

Δx

). (39)

Множитель Лоренца

Предполагается, что кристалл малых размеров: 10

–4

…10

–3

м. Одна-

ко на самом деле размеры больше, но кристалл состоит из отдельных

блоков, слегка разориентированных относительно друг друга (от долей

минут до долей градуса). Если блоки малы, а их отклонение от средней

ориентировки по кривой Гаусса, то это – идеально-мозаичный кристалл

Отражения будут в интервале ±

, а интенсивность рассеяния будет за-

висеть от угла следующим образом:

• L(Θ) =

Θ2sin

– для монокристалла;

• L(Θ) =

ΘΘcossin

– для поликристалла.

Обычно множитель Лоренца комбинируют с формулой Томсона:

• L(Θ)P(Θ) =

Θ+

2sin

2cos1

– для монокристалла;

• L(Θ)P(Θ) =

ΘΘ

Θ+

cossin

2cos1

– для поликристалла.

Множитель поглощения

I = I

hkl

– для плоского толстого образца, где

– коэффициент

поглощения; Q

hkl

– отражательная способность плоскости (hkl):

hkl

= L(Θ)P(Θ)F

hkl

exp(–2M). (40)

Множитель повторяемости

Обозначим р – число эквивалентных плоскостей в ячейке; оно за-

висит от симметрии кристалла. Например, для кубического кристалла

число разных плоскостей в ячейке различно:

• {100} – р = 6, (это 100, 010, 001, 100, 010, 001);

• {110} – p = 12;

• {111} – p = 8;

• {hho}и {hhl} – p = 24;

• {hkl} – p = 48.

Рис. 17. Взаимодействие лучей при многократном отражении

Следовательно, при прохождении рентгеновского пучка через кри-

сталл на его пути будет встречаться разное число разных плоскостей,

т. е. интенсивность отраженного луча будет пропорциональна этим чис-

лам, рис. 17.

Понятие о динамической теории рассеяния

Отраженные лучи от какой-либо плоскости имеют сдвиг на

/2, а

дважды – на

. Поэтому, когда падающий луч S

попадает в кристалл

под углом Вульфа–Брэгга (т. е. плоскость находится в отражающем по-

ложении), то первичный пучок ослабляется дважды отраженным. Это

явление называется первичной экстинкцией, т. е. ослабление первич-

ного пучка определяется не только коэффициентом поглощения среды,

но и суммой

, где

≠ 0 только при угле Вульфа–Брэгга. Она раз-

личная для разных плоскостей, т. к. отражательная способность их не-

одинакова. Таким образом, если кристалл не находится в отражающем

положении, то он поглощает рентгеновский пучок только в соответст-

вии с законом поглощения. Если же он находится в отражающем поло-

жении, то происходит

многократное рассеяние с изменением каждый

раз фазы на

/2 и, следовательно, дополнительное заметное ослабление

проходящего через кристалл пучка.

Существует явление, называемое вторичной экстинкцией

– экра-

нирование нижних блоков верхними, рис. 18. Величина эффекта зависит

от вероятности нахождения на пути к блоку 2 блока 1, которая умень-

шается с увеличением угла мозаичности.

Этот эффект наблюдается, если кристалл мозаичный, причем блоки

немного разориентированы. Тогда вместо интенсивности, определяемой

выражением exp(–

t), на нижний блок попадет меньшая интенсивность,

если на пути луча встретится блок с равной (примерно) ориентацией,

как и нижний. Влияние на рентгеновский пучок первичной и вторичной

экстинкции можно разделить, т. к. их зависимости от угла дифракции

различны.

Рис. 18. Схема возникновения вторичной экстинкции

1.6. Экспериментальные методы рентгеноструктурного анализа

Выбор метода исследования определяется необходимостью полу-

чения максимальной информации и зависит от состояния образца. Два

случая: моно- и поликристаллическое состояние. Второй случай встре-

чается гораздо чаще, однако методы монокристаллов позволяют полу-

чать информацию о структуре более просто.

В рентгеноструктурном анализе используют три основных метода:

1. Метод порошков

(поликристаллов). Используется монохромати-

ческое излучение.

2. Метод Лауэ

. Используется непрерывный рентгеновский спектр и

неподвижный монокристалл. Неподвижная фотопленка.

3. Метод вращения монокристалла

. Монохроматический рентге-

новский пучок облучает колеблющийся или вращающийся монокри-

сталл. Пленка неподвижна.

Метод порошков

Геометрия съемки

Построение сферы отражения, рис. 19, показывает, что получается

пересечение двух сфер: сферы Эвальда и сферы обратной решетки, при

этом дифракционные лучи лежат на поверхности конусов с основанием

и растром 4Θ.

Порошковые рентгенограммы дают только длины векторов обрат-

ной решетки, но не дают взаимного расположения этих векторов.

Таким образом, схема рентгеновской камеры представлена на

рис. 20.

Рис. 19. Сфера отражения