Кудрявцев А.А. Пособие по теории вероятностей
Подождите немного. Документ загружается.


x
i
m
i
m(x)
x =
R
xm(x) dx
R
m(x) dx
. (8.7)
g : IR
n
−→ IR
σ B
n
g
−1
(B) ≡ {x ∈ IR
n
|g(x) ∈ B} ∈ B
n
B ∈ B
σ B
n
σ
IR
n
σ σ
B
1
× . . . × B
n
B
i
∈ B i = 1, . . . , n
(IR
n
, B
n
)
ξ g(x)
Eg(ξ) ≡
Z
x dF
g(ξ)
(x) =
Z
g(x) dF
ξ
(x).
ξ B P(B) > 0
x
F (x|B) = P(ξ < x|B).

ξ B P(B) > 0
E(ξ|B) =
Z
x dF (x|B),
F (x|B) ξ
B
1
, . . . , B
n
F (x|B
1
), . . . , F (x|B
n
)
ξ
F (x) ξ
F (x) =
n
X
i=1
P(B
i
)F (x|B
i
).
ξ
Eξ =
n
X
i=1
P(B
i
)E(ξ|B
i
). (8.8)
B
i
n
∞
ξ
1
, . . . , ξ
n
B
i
∈ B i = 1, . . . , n
P(ξ
1
∈ B
1
, . . . , ξ
n
∈ B
n
) = P(ξ
1
∈ B
1
) · . . . · P(ξ
n
∈ B
n
).
E(a + bξ) = a + bEξ, a, b ∈ IR
E(ξ + η) = Eξ + Eη

P(a ≤ ξ ≤ b) = 1 a ≤ Eξ ≤ b a, b ∈ IR
|Eξ| ≤ E|ξ|
P(ξ ≤ η) = 1 Eξ ≤ Eη
ξ ≥ 0 Eξ = 0 ξ = 0
P(A) = EII
ω
(A) II
ω
(A) = 1 ω ∈ A II
ω
(A) = 0 ω 6∈ A
ξ η g(x, y) g
1
(x) g
2
(y)
g(x, y) = g
1
(x)g
2
(y) P(g
1
(ξ) ≥ 0) = 1 P(g
2
(η) ≥
0) = 1 Eg
1
(ξ) Eg
2
(η) Eg(ξ, η) = Eg
1
(ξ)Eg
2
(η)
Eg(ξ, η)
Eg
1
(ξ) Eg
2
(η)
ξ η Eξη = EξEη
II
ω
(A)
A
ξ
2
η
ξ
2
η
Eξ
2
= −1 ·
1
2
+ 1 ·
1
2
= 0.
η
f
η
(x)
F
η
(x) f
η
(x) = 1/(2
√
x) x ∈ [0, 1] f
η
(x) = 0
x /∈ [0, 1]
Eη =
1
Z
0
x
1
2
√
x
dx =
1
3
.
ξ
2
+ η ξ
2
η
ξ
2
η

E(ξ
2
+ η) = Eξ
2
+ Eη = 1/3
24
0.4
0.8
ξ
A B
P(B) = 2P(A) = 2/3
{ }
ξ
n
n = 1, . . . , 24
n
ξ =
24
X
n=1
ξ
n
.
ξ
n
A B
Eξ
n
= P(A)E(ξ
n
|A) + P(B)E(ξ
n
|B).
A ξ
n
1 0.4 B
0.8
Eξ
n
=
1
3
(0 · 0.6 + 1 · 0.4) +
2
3
(0 · 0.2 + 1 · 0.8) =
2
3
.
Eξ
16
ξ
Eξ = P(ξ ≥ 1) + P(ξ ≥ 2) + . . . + P(ξ ≥ n) + . . . .

1
F (x)
x
1
2
1
1
2
0
ξ η
Eξ = Eη Eξ/η = Eη/ξ Eξ/(ξ+η) =
Eη/(ξ + η) E1/ξ = E1/η
ξ η
Eξ Eη E max{ξ, η}
Eξ = 0 E|ξ| = 1 E max{0, ξ} E min{0, ξ}
ξ
P(ξ ≥ 0) = 1 F(x)
Eξ Eξ =
R
+∞
0
(1 −F (x)) dx
ξ
a E|ξ + a| ≥ E|ξ|
ξ
x
max{x, Eξ} ≤ E max{x, ξ}
ξ
Eξ E(1/ξ)
ξ
η
ζ
ξ
[0, 2π] η
1
= cos ξ η
2
= sin ξ Eξ Eη
1
Eη
2
η
1
η
2
ξ ∼ K(0, 1) Eξ
ξ Eξ

(Ω, F, P)
ξ
ξ
Dξ = E(ξ − Eξ)
2
.
min
a
E(ξ − a)
2
,
a = Eξ
Eξ ξ
√
Dξ
Dξ = Eξ
2
− (Eξ)
2
Dξ ≥ 0 Dξ = 0 ξ = const
D(a + bξ) = b
2
Dξ a, b ∈ IR
ξ η D(ξ + η) =
Dξ + Dη
D(ξ + η) = E(ξ + η)
2
− (Eξ + Eη)
2
=
= Eξ
2
+ 2Eξη + Eη
2
− (Eξ)
2
− 2EξEη − (Eη)
2
=
= Eξ
2
− (Eξ)
2
+ Eη
2
− (Eη)
2
= Dξ + Dη.

D(ξ + η) = Dξ + Dη + 2(Eξη − EξEη).
ξ η
(ξ, η) = Eξη − EξEη = E(ξ − Eξ)(η − Eη).
ξ η
ρ(ξ, η) =
(ξ, η)
√
Dξ
√
Dη
.
ξ η
(ξ, η) = 0 ρ(ξ, η) = 0
D(ξ + η) = Dξ + Dη + 2 (ξ, η)
k ξ
Eξ
k
k
ξ E(ξ − Eξ)
k
k ξ E|ξ|
k
k ξ
E|ξ − Eξ|
k
k ξ
Eξ
[k]
= Eξ(ξ − 1) . . . (ξ − k + 1)
r q ≤ r
q
r > q
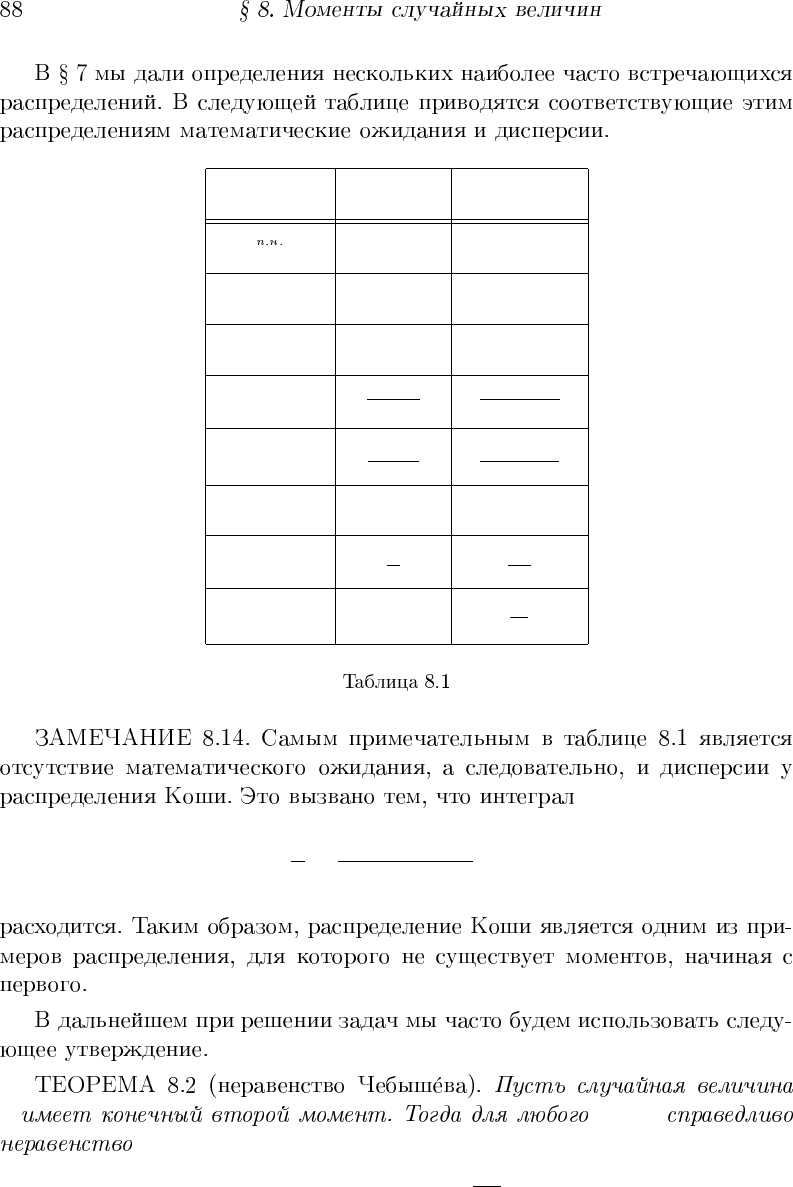
P
ξ
Eξ Dξ
ξ = a a 0
Bi(n, p) np np(1 − p)
P ois(λ) λ λ
G(p)
p
1 − p
p
(1 − p)
2
R[a, b]
a + b
2
(a − b)
2
12
N(a, σ
2
) a σ
2
exp(λ)
1
λ
1
λ
2
K(a, σ) ∞ − ∞
1
π
Z
σx
σ
2
+ (x − a)
2
dx
ξ ε > 0
P(|ξ − Eξ| ≥ ε) ≤
Dξ
ε
2
. (8.9)

ξ
2
η
ξ
2
η
g(x) = x
2
ξ
2
Dξ
2
= Eξ
2
2
−(Eξ
2
)
2
= 1 −0 = 1
Dη = Eη
2
− (Eη)
2
=
1
Z
0
x
2
1
2
√
x
dx −
1
9
=
1
5
−
1
9
=
4
45
.
ξ
1
, . . . , ξ
n
P(ξ
1
= 1) = P(ξ
1
= −1) = 1/4 P(ξ
1
= 0) = 1/2
S
n
=
ξ
1
+ . . . + ξ
n
ξ
1
Eξ
1
= 1 ·
1
4
+ 0 ·
1
2
− 1 ·
1
4
= 0,
Dξ
1
= Eξ
2
1
= 1 ·
1
2
+ 0 ·
1
2
=
1
2
.
ξ
i
ES
n
= E
n
X
i=1
ξ
i
=
n
X
i=1
Eξ
i
= n · 0 = 0.
ξ
i
DS
n
= D
n
X
i=1
ξ
i
=
n
X
i=1
Dξ
i
= n ·
1
2
=
n
2
.
η
1
, η
2
, . . .
Bi(1, 1/2) ξ
i
ξ
i
= η
i
− η
i+2
i = 1, 2, . . .
ξ
1
, ξ
2
, . . . ξ
1
ξ
i

ξ
i+j
j ∈ IN j 6= 2
S
n
= ξ
1
+ . . . + ξ
n
n ≥ 2
P(ξ
1
= 1) η
i
P(ξ
1
= 1) = P(η
1
− η
3
= 1) = P(η
1
= 1, η
3
= 0) = P(η
1
= 1)P(η
3
= 0) =
1
4
.
P(ξ
1
= 0) P(ξ
1
= −1)
ζ
1
ζ
2
P(ζ
1
= x
1
, ζ
2
= x
2
) = P(ζ
1
= x
1
)P(ζ
2
=
x
2
) x
1
x
2
j 6= 2
P(ξ
i
= 1, ξ
i+j
= −1) = P(η
i
= 1, η
i+2
= 0, η
i+j
= 0, η
i+j+2
= 1) =
= P(η
i
= 1)P(η
i+2
= 0)P(η
i+j
= 0)P(η
i+j+2
= 1) =
1
4
·
1
4
=
= P(ξ
i
= 1)P(ξ
i+j
= −1).
ξ
i
ξ
i+j
ES
n
= 0
DS
n
ξ
i
ξ
i+2
P(ξ
i
= 1, ξ
i+2
= 1) 6=
P(ξ
i
= 1)P(ξ
i+2
= 1) ES
2
n
= DS
n
ξ
i
ξ
j
ξ
2
i
i = j
η
1
η
3
− η
2
3
− η
1
η
5
+ η
3
η
5
|i − j| = 2
ES
2
n
= E
n
X
i=1
ξ
i
!
2
= E
n
X
i=1
ξ
i
·
n
X
j=1
ξ
j
=
= E
X
i, j: i=j
ξ
i
ξ
j
+
X
i, j: |i−j|=2
ξ
i
ξ
j
+
X
i, j: |i−j|6=0, 2
ξ
i
ξ
j
=
= nEξ
2
1
+ 2(n − 2)E(η
1
η
3
− η
2
3
− η
1
η
5
+ η
3
η
5
) + (n
2
− n − 2(n − 2))Eξ
1
Eξ
2
=
= n ·
1
2
+ 2(n − 2)
1
4
−
1
2
−
1
4
+
1
4
+ (n
2
− 3n + 4) · 0 = 1.
η
n
n
