Кудрявцев А.А. Пособие по теории вероятностей
Подождите немного. Документ загружается.


ω
Ω
Ω
Ω
Ω = { , , , },
Ω
Ω = { , , , . . . , , . . .}.

Ω
A
ω ∈ A
A
A = {
} B = { }
A
B
A = { , } B = { , , }
Ω
Ω
A B
A
B A ∪ B
A B
A B AB A ∩ B
A B
A
B A\B
Ω
∅ = Ω\Ω
Ω Ω ⊂ Ω ∅ ⊂ Ω
A = Ω\A
A
A B
AB = ∅
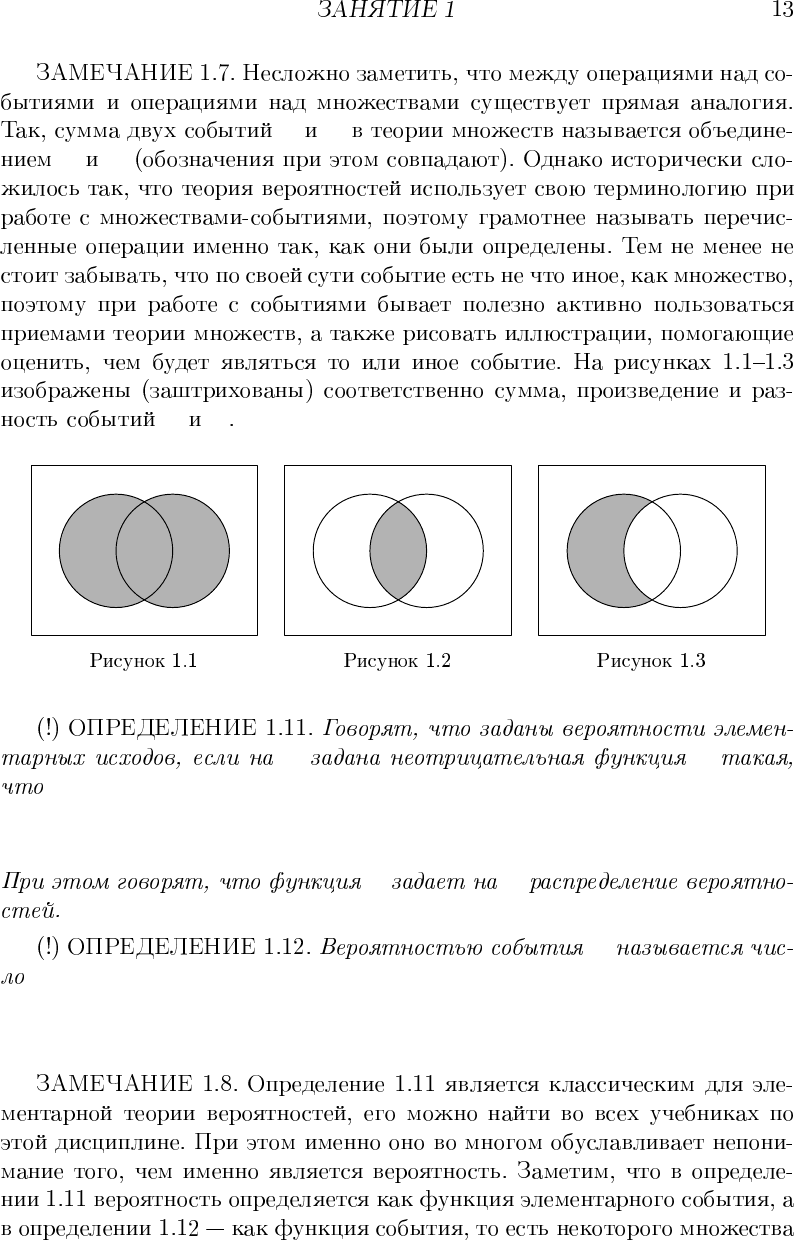
A B
A B
A B
Ω
A B
Ω
A B
Ω
A B
Ω P
X
ω∈Ω
P(ω) = 1. (1.1)
P Ω
A
P(A) =
X
ω∈A
P(ω). (1.2)

Ω Ω
X
ω∈Ω
P({ω}) = 1
P(A) =
X
ω∈A
P({ω})
Ω
A B
C
D
D = (A ∪ B ∪ C)\(A\(B ∪ C))\(B\(A ∪ C))\(C\(A ∪B))\ABC,
P(D)
ABC AB AC BC
P(D) = P(AB) + P(AC) + P(BC) − 3P(ABC). (1.3)

P(∅) = 0 P(Ω) = 1
P(A ∪ B) = P(A) + P(B) − P(AB)
P(A) = 1 − P(A)
A
P(A)
Ω
P({ }) = 0.1 P({ }) = 0.2 P({ }) = 0.3 P({ }) = 0.4
P
A = { , , } P(A) =
0.1 + 0.2 + 0.3 = 0.6
1/2
A n
A

A n
P(A) = lim
n→∞
n
A
n
. (1.4)
{n
A
/n}
n≥1
Ω n ω
1
, . . . , ω
n
P({ω
i
}) = 1/n i = 1, . . . , n
A
P(A) =
|A|
|Ω|
=
A
n
.
|A| A
P
36

36 C
3
36
A
C
1
4
32
C
2
32
|A| = C
1
4
C
2
32
P(A) = C
1
4
C
2
32
/C
3
36
≈
0.2779
A
A
32 C
3
32
A
A
1
A
2
A
3
C
1
4
C
2
32
C
2
4
C
1
32
C
3
4
C
0
32
P(A) = 1 −
C
3
32
C
3
36
=
C
1
4
C
2
32
C
3
36
+
C
2
4
C
1
32
C
3
36
+
C
3
4
C
3
36
≈ 0.3053.
49
6
4 5 6
4 5 6
{
} {
}

2 4 6 7 8 11 12 13
n
28 5
n
N n
1, . . . , N
n
1
, . . . , n
N
n
1
+ . . . + n
N
= n
K L M
n
k l m
k + l + m = n
n + k
n
m ≤ n
{ } {
}

G
g
G
g
G
g
g
G
p =
mes g
mes G
. (2.1)
mes
p G
G

G
g
AB
A B
G
g
g
G
1/2
A
B
G
g
A
B g
G
1/3
