Куцый Н.Н. Теория автоматического управления. Лабораторный практикум
Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ PОССИЙСКОЙ ФЕДЕPАЦИИ
ИPКУТСКИЙ ГОСУДАPСТВЕHHЫЙ
ТЕХHИЧЕСКИЙ УHИВЕPСИТЕТ
Ф а к у л ь т е т к и б е р н е т и к и
ТЕОРИЯ
ТЕОРИЯ
АВТОМАТИЧЕСКОГО
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
УПРАВЛЕНИЯ
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
Лабораторные работы № 1, 2, 3, 4, 5.
Иркутск - 2000 г.
Куцый Н.Н. Теория автоматического управления. Лабораторный практи-
кум: Лабораторные работы № 1,2,3,4,5. – Иркутск, изд-во Иркутск. гос. технич.
ун-та, 2000. – 64с.
Приведены варианты заданий лабораторных по учебной дисциплине "Тео-
рия управления". Дан необходимый теоретический и справочный аппарат.
Предназначен для студентов специальностей 220100 – "Вычислительные маши-
ны, системы, сети и комплексы", 220200 – "Автоматизированные системы об-
работки информации и управления", 071900 – "Информационные системы в
технике и технологиях".
Библиогр. 8 назв.
Рецензент:
Подготовила к печати: Брянская А.Г.
План 1999. 2,4 печ. л., 2,5 уч.-изд. л. Тираж 100 экз. Зак. 255.
ЛР № 020263 от 30.12.96
Иркутский государственный технический университет
664074, Иркутск, ул. Лермонтова, 83
2

ЛАБОРАТОРНАЯ РАБОТА № 1
МОДЕЛИРОВАНИЕ ЗВЕНЬЕВ АВТОМАТИЧЕСКИХ СИСТЕМ
Цель работы - ознакомление с методами моделирования автоматических
систем; непосредственное моделирование типовых звеньев; расчет временных
характеристик звеньев
1.ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
В настоящее время для анализа и синтеза автоматических систем широко
применяется математическое моделирование, при котором автоматические си-
стемы можно моделировать по уравнению (по уравнениям) или по структурной
схеме. Более наглядным является подход, при котором схема моделирования
соответствует структурной схеме автоматической системы. В этом случае воз-
никает необходимость моделирования дробно-рациональных передаточных
функций вида
,
,
...
...
)( )1(
01
1
1
01
1
1
nm
apapap
bpbpbpb
pW
n
n
n
m
m
m
m
≤
++++
++++
=
−
−
−
−
где
−
−−
011011
,,...,,,,...,, aaabbbb
nmm
заданные постоянные коэффициенты; p -
комплексная переменная.
Известны различные способы моделирования таких передаточных функ-
ций, среди которых наибольшее распространение нашли способы, позволяю-
щие осуществлять моделирование при заранее неизвестном законе изменения
входного сигнала и избегать применения численного дифференцирования, ко-
торое, как известно, весьма восприимчиво к неточностям представления тех
или иных координат звеньев, автоматических систем [1]:
- непосредственное интегрирование;
- разложение на уравнения первого порядка;
- комбинирование производных.
Способ непосредственного интегрирования. Передаточной функции
вида (1) соответствует дифференциальное уравнение вида
....
... )2(
01
1
1
1
01
1
1
1
gb
dt
dg
b
dt
gd
b
dt
gd
b
ya
dt
dy
a
dt
yd
a
dt
yd
n
n
n
n
n
n
n
n
n
n
n
++++=
=++++
−
−
−
−
−
−
Требуется найти y(t) при заданных постоянных коэффициентах
,
ji
ba
;1)1(0(
−=
ni
))1(0 nj
=
и воздействии g, зависимость которого от времени зара-
нее не задана.
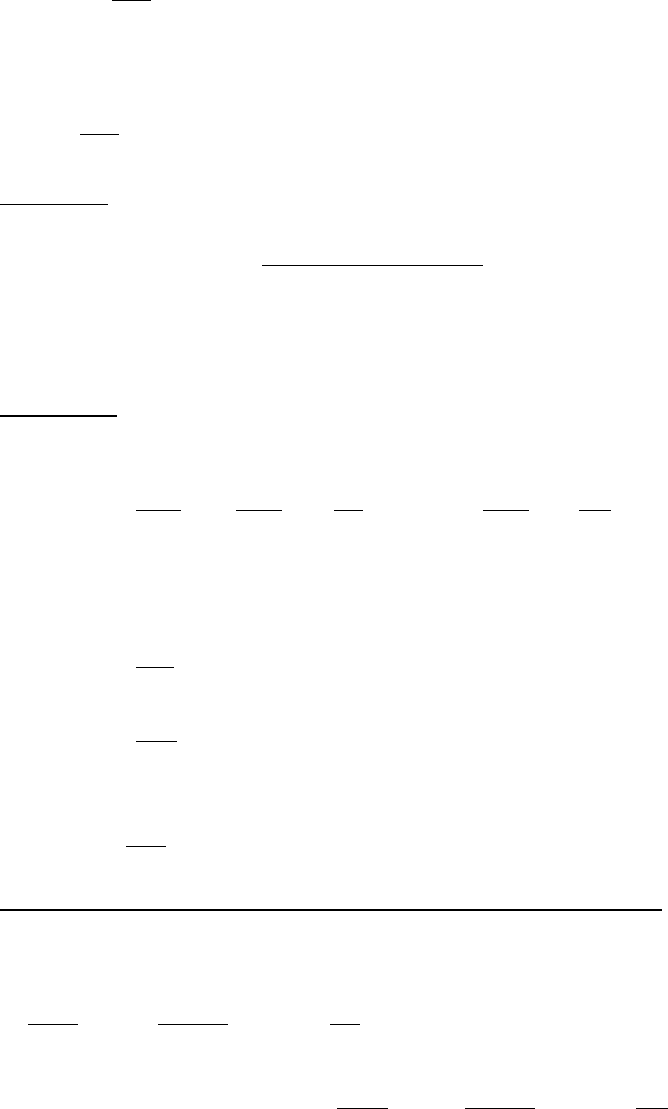
Запишем
gbzy
n
+=
1
)3(
и
.)( )4(
211
1
zgbya
dt
dz
nn
+−−=
−−
Для определения
2
z
воспользуемся обобщенным выражением
.0 ),,...,2,1( ,)( )5(
11
==+−−=
++−−
nkknkn
k
znkzgbya
dt
dz
Пример. Задана передаточная функция
.)(
01
2
2
3
01
2
2
apapap
bpbpb
pW
+++
++
=
Представить уравнения моделирования на основе способа непосредствен-
ного интегрирования.
Решение. Запишем соответствующее заданной передаточной функции
дифференциальное уравнение
.
01
2
2
201
2
2
2
3
3
gb
dt
dg
b
dt
gd
bya
dt
dy
a
dt
yd
a
dt
yd
++=+++
Здесь
.2 ,3
==
mn
Так как
,0
3
=
b
то исходя из выражения (3) имеем
.
1
zy
=
Далее
311
2
222
1
)(
,)(
zgbya
dt
dz
zgbya
dt
dz
+−−=
+−−=
и
).(
00
3
gbya
dt
dz
−−=
Способ разложения на уравнения первого порядка. Перепишем диффе-
ренциальное уравнение (2) в виде
....
... )6(
01
1
1
1
01
1
1
1
gb
dt
dg
b
dt
gd
b
dt
gd
b
ya
dt
dy
a
dt
yd
a
dt
yd
n
n
n
n
n
n
n
n
n
n
n
++++=
=++++
−
−
−
−
−
−
Это линейное дифференциальное уравнение может быть представлено в
виде совокупности линейных дифференциальных уравнений первой степени
4
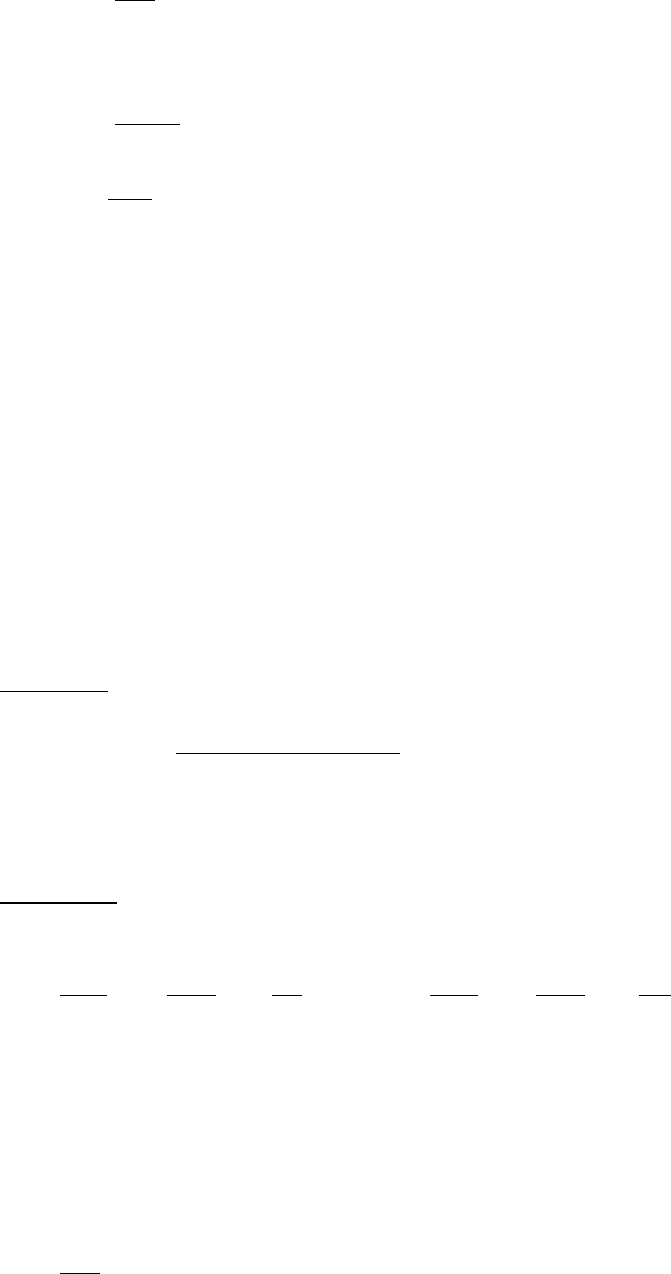
. . . . )7(
,
,
12
1
1
gy
dt
dy
gyy
n
n
−
+=
+=
α
α
....
,
01021121
1
1
gyayayaya
dt
dy
gy
dt
dy
nnnn
n
n
n
α
α
+−−−−−=
+=
−−−
−
Чтобы уравнения (6) и (7) были тождественны, необходимо, чтобы значе-
ния новых коэффициентов
))1(0( ni
i
=
α
удовлетворяли следующим равенствам
....
,...
,...
. . . . . . . . .
,
,
011221100
1211211
23122
111
aaaab
aaab
aab
ab
b
nnnn
nnn
nn
nnnn
nn
ααααα
αααα
ααα
αα
α
+++++=
++++=
+++=
+=
=
−−−
−−
−
−−−
Пример. Задана передаточная функция
.)(
01
2
2
3
01
2
2
apapap
bpbpb
pW
+++
++
=
Представить уравнения моделирования на основе способа разложения на
уравнения первого порядка.
Решение. Запишем соответствующее заданной передаточной функции
дифференциальное уравнение
.
01
2
2
2
3
3
301
2
2
2
3
3
gb
dt
dg
b
dt
gd
b
dt
gd
bya
dt
dy
a
dt
yd
a
dt
yd
+++=+++
Здесь для того, чтобы записать это уравнение в форме (5) пришлось доба-
вить
0
3
=
b
и тем самым выровнять степени правой и левой частей дифферен-
циального уравнения. Так как
,3
=
n
то совокупность линейных дифференци-
альных уравнений будет иметь вид
,
,
22
1
31
gy
dt
dy
gyy
α
α
+=
+=
5
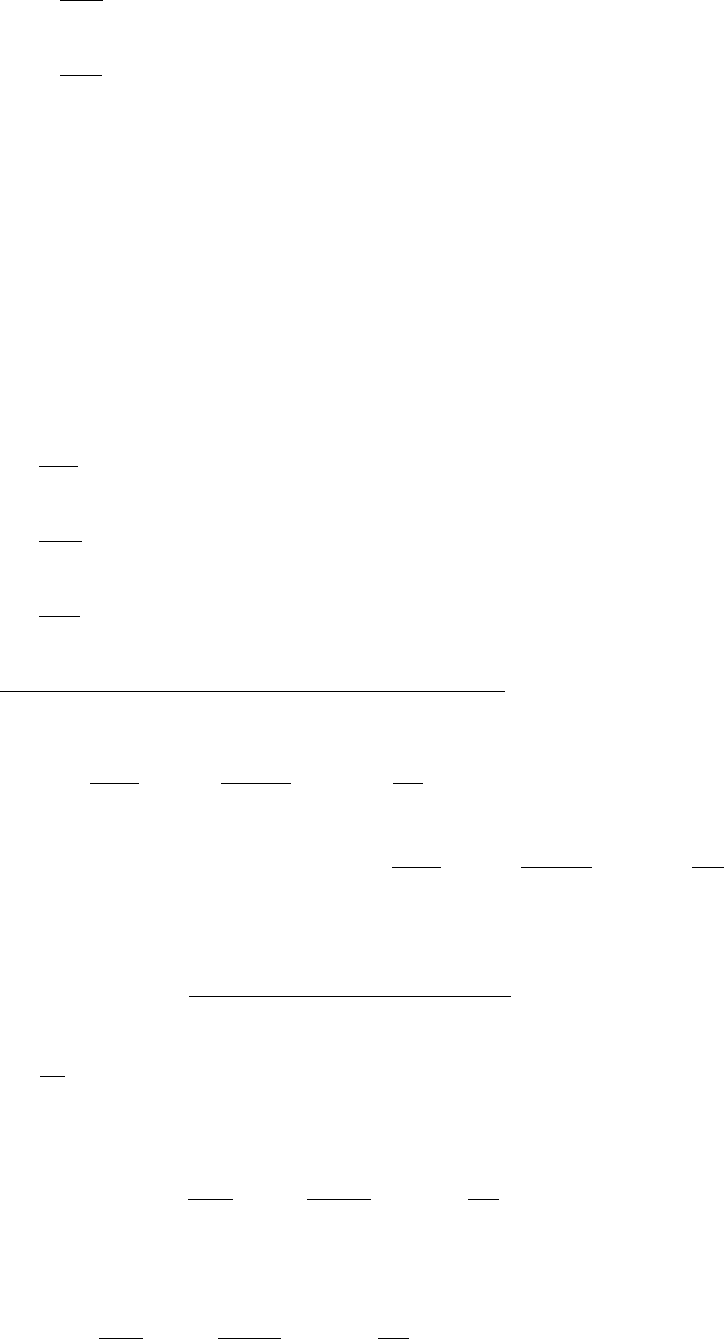
.
,
0102132
3
13
2
gyayaya
dt
dy
gy
dt
dy
α
α
+−−−=
+=
Составим выражения для определения коэффициентов
30
,...,
αα
. Так как
0
3
=
b
, то
0
3
=
α
и
.
,
,
122100
2211
22
aab
ab
b
ααα
αα
α
++=
+=
=
Тем самым
.))((
,)(
,
,
1222210102132
3
2213
2
22
1
1
gabaabbbyayaya
dt
dy
gabby
dt
dy
gby
dt
dy
yy
+−−+−−−=
−+=
+=
=
Способ комбинирования производных. Перепишем дифференциальное
уравнение (2) в виде
....
... )8(
01
1
1
1
01
1
1
1
gb
dt
dg
b
dt
gd
b
dt
gd
b
ya
dt
dy
a
dt
yd
a
dt
yd
n
n
n
n
n
n
n
n
n
n
n
++++=
=++++
−
−
−
−
−
−
Это уравнение расчленим на два, вводя новую переменную
,
...
)9(
01
1
1
apapap
g
u
n
n
n
++++
=
−
−
где
−=
dt
d
p
оператор дифференцирования.
В результате получаем
.... )10(
01
1
1
1
ub
dt
du
b
dt
ud
b
dt
ud
by
n
n
n
n
n
n
++++=
−
−
−
Выражение (9) можно переписать в дифференциальной форме
.... )11(
01
1
1
1
gua
dt
du
a
dt
ud
a
dt
ud
n
n
n
n
n
=++++
−
−
−
6

Пример Задана передаточная функция
.)(
01
2
2
3
01
2
2
apapap
bpbpb
pW
+++
++
=
Представить уравнения моделирования на основе способа комбинирова-
ния производных.
Решение. Запишем соответствующее заданной передаточной функции
дифференциальное уравнение
.
01
2
2
2
3
3
301
2
2
2
3
3
gb
dt
dg
b
dt
gd
b
dt
gd
bya
dt
dy
a
dt
yd
a
dt
yd
+++=+++
Здесь для того, чтобы записать это уравнение в форме (8) пришлось доба-
вить коэффициент
0
3
=
b
и тем самым выровнять степени правой и левой ча-
стей дифференциального уравнения.
Исходя из выражения (10) имеем
,
01
2
2
2
3
3
3
ub
dt
du
b
dt
ud
b
dt
ud
by
+++=
или с учетом
0
3
=
b
.
01
2
2
2
ub
dt
du
b
dt
ud
by
++=
Выражение (11) в рассматриваемом примере принимает вид
.
01
2
2
2
3
3
gua
dt
du
a
dt
ud
a
dt
ud
=+++
Решение дифференциальных уравнений, в правой части которых при-
сутствует единичная ступенчатая функция 1( t ) и ее производные
Покажем подход к решению дифференциальных уравнений вида
,...
... )12(
01
1
1
1
01
1
1
1
gb
dt
dg
b
dt
gd
b
dt
gd
b
ya
dt
dy
a
dt
yd
a
dt
yd
a
m
m
m
m
m
m
n
n
n
n
n
n
++++=
=++++
−
−
−
−
−
−
где
)(1)( ttg
=
и соответственно
=
′
==
m
m
dt
gd
t
dt
gd
t
dt
dg
),...,(),...,(
2
2
δδ
).(
1
t
m
−
δ
Суть этого подхода заключается в сведении неоднородного уравнения к
однородному.
Установившееся значение переменной y при
∞→
t
найдем, положив в (12)
все производные равными нулю
7

∞→
t
lim )13(
.)(
0
0
a
b
yty
уст
==
Это установившееся значение представляет собой частное или вынужден-
ное решение неоднородного уравнения (12), т.е.
.)(
уств
yty
=
Введем новую переменную
.)()()()( )14(
уств
ytytytytz
−=−=
Решение неоднородного уравнения (12) для
)(tz
может быть записано в
виде
....)()( )15(
21
21
tp
n
tptp
уст
n
CCСytytz
+++=−=
Этому решению соответствует дифференциальное уравнение без правой
части
.0... )16(
0
1
1
1
=+++
−
−
−
za
dt
zd
a
dt
zd
a
n
n
n
n
n
n
Из уравнения (14) можно определить связь между начальными условиями
для исходной переменной y и новой переменной z при t=0
.,..., ,
)1(
0
)1(
00000
−−
=
′
=
′
−=
nn
уст
yzyzyyz
После нахождения решения для переменной z по формуле (14) можно вер-
нуться к исходной переменной y смещением решения на величину
.
уст
y
Однако эти рассуждения пока справедливы для случая, когда правая часть
дифференциального уравнения имеет размерность
,0
=
m
т.е.
....
001
1
1
1
gbya
dt
dy
a
dt
yd
a
dt
yd
a
n
n
n
n
n
n
=++++
−
−
−
Это происходит потому, что, вообще говоря, необходимо различать на-
чальные условия, которые существовали в автоматической системе до прило-
жения возмущения, т.е. при времени
,0
−
=
t
и непосредственно сразу после его
приложения, т.е. при времени
.0
+
=
t
Остановимся на этом вопросе более по-
дробно в случае приложения возмущения типа ступенчатой функции.
Для простоты расчетов для времени
0
−
=
t
в большинстве практических
случаев принимают нулевые начальные условия, т.е.
0 ,0 ,0
000
=
′′
=
′
=
−−−
yyy
и
т.д. В дальнейшем под нулевыми начальными условиями будем понимать
именно эти равенства.
Начальные условия, которые будут иметь место непосредственно после
приложения ступенчатой функции, т.е. при
0
+
=
t
(обозначим их
000
, ,
+++
′′′
yyy
и
т.д.), можно определить из исходного дифференциального уравнения (12). Не
8
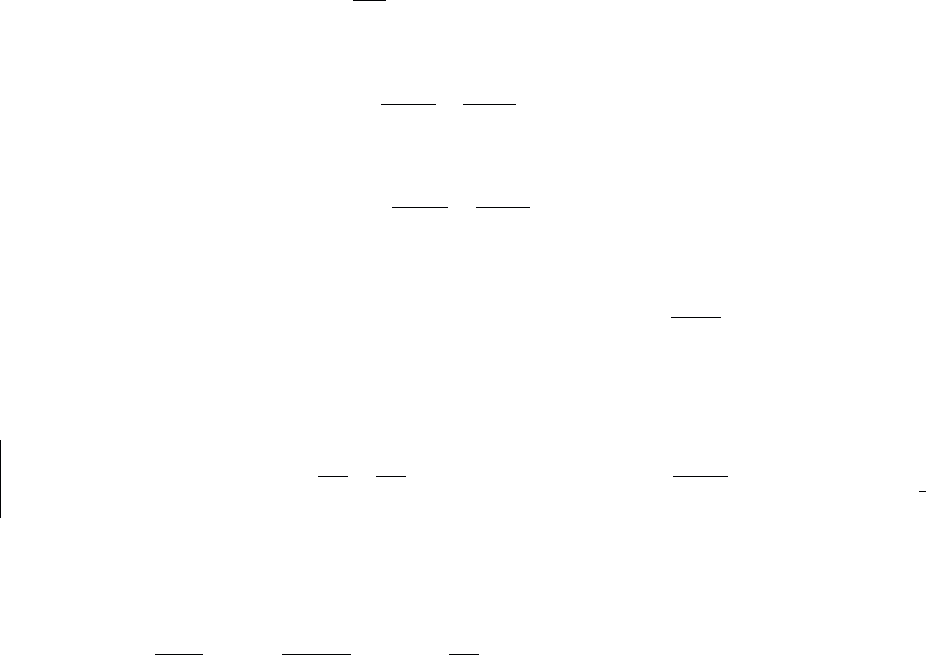
останавливаясь на доказательстве, приведем конечные результаты. для первых
1
−−
mn
начальных условий имеют места равенства
=
′
=
′
=
−−
−
−−
+
−+
−+
)1(
0
)1(
0
00
00
. . .
,
,
)16(
mnmn
yy
yy
yy
.
Таким образом, для самой координаты и первых
)1(
−−
mn
производных
нулевые начальные условия сохраняются и после приложения ступенчатой
функции.
Для остальных начальных условий выполняются соотношения
, )17(
)(
0
)(
0
n
m
mnmn
a
b
yy
+=
−
−
−
+
( )
,
)(
0
)(
0
11
)1(
0
)1(
0
mnmn
n
n
n
m
mnmn
yy
a
a
a
b
yy
−
−
−
+
−−
+−
−
+−
+
−−+=
( )
( )
,
)1(
0
)1(
0
1
)(
0
)(
0
22
)2(
0
)2(
0
+−
+
+−
+
−
−
−
−
+
−−
+−
−
+−
+
−
−−−+=
mnmn
n
n
mnmn
n
n
n
m
mnmn
yy
a
a
-
yy
a
a
a
b
yy
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
( ) ( )
....
)2(
0
)2(
0
1
)(
0
)(
0
11
)1(
0
)1(
0
−
−
−
+
−
−
−
−
+
−
−
−
+
−−−−−+=
nn
n
m
mnmn
nn
nn
yy
a
a
yy
a
a
a
b
yy
.
Эти формулы подтверждают вышесказанное, что только при
0
=
m
, т.е.
для дифференциального уравнения
gbya
dt
dy
a
dt
yd
a
dt
yd
a
n
n
n
n
n
n
001
1
1
1
...
=++++
−
−
−
при
)(1)( ttg
=
начальные условия при
0
+
=
t
соответствуют начальным услови-
ям при
0
−
=
t
.
Пример. Найдем реакцию звена на единичную ступенчатую функцию при
нулевых начальных условиях, т.е. переходную функцию, если дифференциаль-
ное уравнение имеет вид
9

.5,04,00,05
2
2
g
dt
dg
y
dt
dy
dt
yd
+=++
Для простоты примем, что переменная
y t( )
является безразмерной величи-
ной. Решим характеристическое уравнение
.014,005,0
2
=++
pp
Его корни
.24
2,1
jjp
±−=±−=
βα
Согласно заданным условиям
0
0
=
−
y
и
.0
0
=
′
+
y
Так как в данном случае
2
=
n
и
,1
=
m
то начальные условия для
,0
+
=
t
в соответствии с (16) и (17), будут
.10
05,0
5,0
0
,0
2
1
00
00
=+=+
′
=
′
==
−+
−+
a
b
yy
yy
Определяем установившееся значение искомой координаты
.1
0
0
==
a
b
y
уст
Введем новую переменную
.1)()(
−=
tytz
Начальные условия для новой
переменной
.10
,110
00
00
=
′
=
′
−=−=−=
++
++
yz
yyz
уст
Для
2
=
n
и в случае комплексно-сопряженных корней решение дифферен-
циального уравнения имеет вид
,)sincos(
t
tCtBz
α
ββ
−
+=
где
,1
0
−==
+
zB
.3
2
104
00
=
+−
=
′
+
=
++
β
α
zz
C
Таким образом
.)2sin32cos(
4
t
ttz
−
+−=
10
