Куцый Н.Н. Теория автоматического управления. Лабораторный практикум
Подождите немного. Документ загружается.

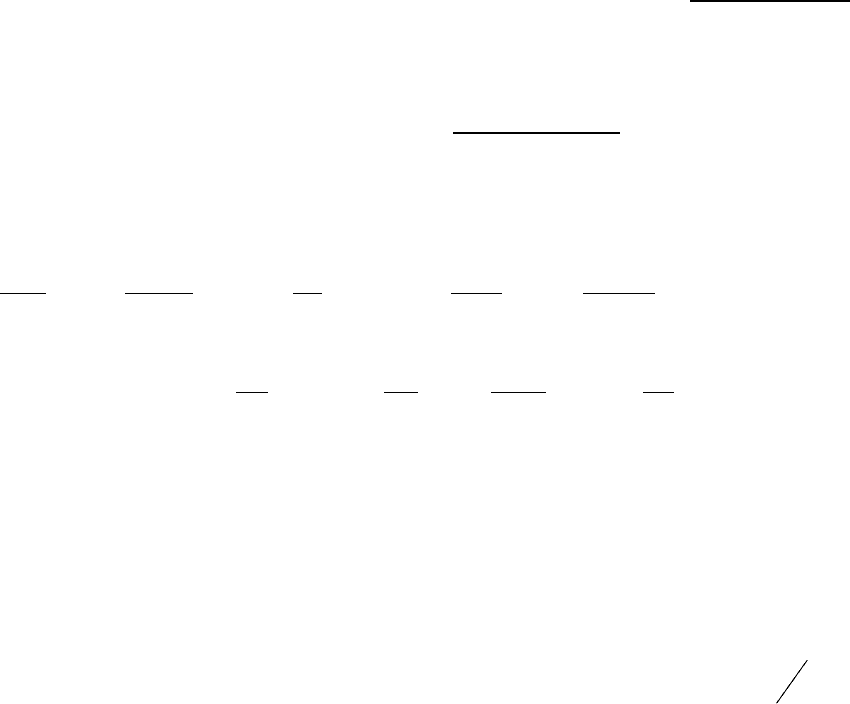
некоторому конечному значению, то такую систему называют нейтральной
(нейтрально устойчивой).
Если свободная составляющая управляемой переменной неограниченно
возрастает или совершает гармонические колебания с неограниченно возраста-
ющей амплитудой, то такую систему называют неустойчивой.
Рассмотрим условие устойчивости и различные инженерные методы про-
верки автоматических систем на устойчивость.
Пусть дифференциальное уравнение линейной системы имеет вид
,...
... )(
fc
dt
df
c
dt
d
c
dt
td
cgb
dt
dg
b
dt
gd
b
dt
gd
bya
dt
dy
a
dt
yd
a
dt
yd
a
l
l
l
l
l
l
m
m
m
m
m
m
n
n
n
n
n
n
01
1
1
101
1
1
101
1
1
1
1
+++++++
++=++++
−
−
−
−
−
−
−
−
−
или в сокращенной форме записи
,)...()...
()...( )2(
01
1
101
1
101
1
1
fcpcpcpcgbpb
pbpbyapapapa
l
l
l
l
m
m
m
m
n
n
n
n
+++++++
++=++++
−
−
−
−
−
−
где
)(),(),( tfftggtyy
===
соответственно управляемая переменная, задаю-
щее и возмущающее воздействия;
,,,...,,
011
aaaa
nn
−
,,,...,,
011
bbbb
mm
−
−
−
011
cccc
ll
,,...,,
постоянные коэффициенты, при этом
nm
≤
и
nl
≤
;
−=
dt
d
p
оператор дифференцирования.
Для оценки устойчивости автоматической системы должна быть исследо-
вана свободная составляющая решения уравнения (2), т.е. решение однородно-
го уравнения
0)...( )3(
01
1
1
=++++
−
−
yapapapa
n
n
n
n
при начальных условиях
).(),...,(),( )(
)()(
0004
11
−
n
yyy
Общее решение однородного уравнения (3) есть сумма слагаемых, вид
каждого их которых определяется видом корней характеристического уравне-
ния
,... )( 05
01
1
1
=++++
−
−
apapapa
n
n
n
n
причем здесь
ϖα
jp
+=
- комплексная переменная.
Если характеристическое уравнение автоматической системы не имеет
кратных корней, то решение уравнения (3) будет иметь слагаемые вида
1
)1(1 , )6( niA
t
i
i
=
α
и
. ),)(( ),sin( )( nnnnktA
kk
t
k
k
=+=+
212
117
ϕω
α
31
Слагаемые вида (6) соответствуют вещественному корню
,
i
α
а слагаемые
вида (7) соответствуют паре сопряженных корней
,
kk
j
ωα
±
где
−
kki
ωαα
,,
по-
стоянные, а
ki
CA ,
и
−
k
ϕ
постоянные интегрирования, которые зависят от на-
чальных условий и всегда ограничены по абсолютной величине.
При исследовании решения уравнения (3), если какое-нибудь его слагае-
мое неограниченно возрастает по абсолютной величине, то обязательно неогра-
ниченно возрастает по абсолютной величине и вся сумма в целом, причем неза-
висимо от того разные или одинаковые знаки у слагаемых.
Очевидно, что наличие хотя бы одного положительного корня
0
>
i
α
до-
статочно для того, чтобы соответствующее ему слагаемое в решении уравнения
(3) неограниченно возрастало по абсолютной величине. При наличии одной
пары сопряженных корней с положительной вещественной частью
0
>
k
α
в ре-
шении (3) оказывается гармоническое слагаемое с неограниченно возрастаю-
щей амплитудой. В обоих случаях автоматическая система оказывается неу-
стойчивой.
Таким образом, для устойчивости (асимптотической устойчивости) линей-
ной системы необходимо и достаточно, чтобы все корни характеристического
уравнения имели отрицательную вещественную часть. При наличии хотя бы
одного корня с положительной вещественной частью система неустойчива.
Среди корней характеристического уравнения может быть корень, равный
нулю, т.е.
0
=
i
α
или пара чисто мнимых корней, т.е.
.
1,
kkk
p
γ ω
±=
+
Если при
этом вещественные части всех остальных корней отрицательные, то решение
уравнения (3) будет иметь соответственно постоянное слагаемое
i
A
или гармо-
ническое слагаемое с постоянной амплитудой
).sin(
kkk
tC
ϕω
+
В этих случаях
автоматическая система нейтральная.
Корни алгебраического уравнения, как и всякие комплексные числа удоб-
но представлять в виде точек на комплексной плоскости. Для устойчивости ли-
нейной системы необходимо и достаточно, чтобы все корни характеристиче-
ского уравнения лежали слева от мнимой оси на комплексной плоскости (рис.
1). Если хотя бы один вещественный корень или одна пара сопряженных
комплексных корней находится справа от мнимой оси, то система неустойчива
(рис. 2).
Мнимая ось является, следовательно, границей устойчивости. Говорят,
что система находится на границе устойчивости, если имеется нулевой корень
(рис. 3) или пара чисто мнимых корней (рис. 4), а остальные корни "левые". В
первом случае, который имеет место при
,0
0
=
a
уравнения (1) и (2) определя-
ют только скорость
py
изменения выходной координаты
,y
а сама эта пере-
менная
y
будет зависеть еще и от своего начального значения. Во втором слу-
чае в системе возникают незатухающие гармонические колебания с неизменяе-
мой амплитудой.
32
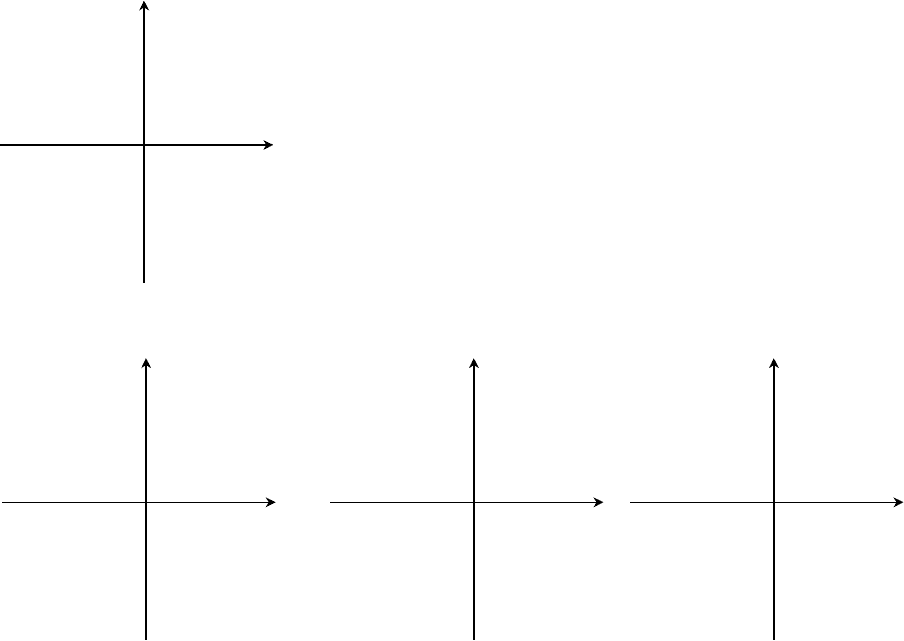
Re
•
•
•
•
Im
Рис. 4.
•
•
•
•
•
•
•
Re
Im
Рис. 1.
•
•
•
•
•
Re
Im
Рис. 2.
•
•
•
•
•
Re
Im
Рис. 3.
На практике для упрощения вычислений устойчивость систем определяют
с помощью некоторых критериев без вычисления корней характеристического
уравнения. Критерий устойчивости – это математическая формулировка усло-
вий, которым удовлетворяют коэффициенты характеристического уравнения
устойчивой системы. Критерии устойчивости эквивалентны по содержанию
сформулированному выше условию устойчивости.
Заметим, что при равенстве нулю
0
a
система находится на границе устой-
чивости. При равенстве нулю какого-либо коэффициента автоматическая си-
стема либо на границе устойчивости, либо неустойчива.
33

Критерии устойчивости разделяют на алгебраические и частотные. К алге-
браическим относят критерий Гурвица и критерий Рауса, к частотным - крите-
рий Михайлова и критерий Найквиста.
Критерий Гурвица удобен для исследования устойчивости автоматических
систем третьего и четвертого порядков, когда известны параметры системы,
кроме того, он позволяет получить аналитическое выражение (выражения) для
границ области возможных значений какого-либо параметра (параметров) ав-
томатической системы, при которых сохраняется устойчивость.
Критерий Рауса широко используют при определении устойчивости авто-
матических систем высокого порядка, если известны числовые значения коэф-
фициентов его характеристического уравнения.
По критериям Гурвица, Рауса и Михайлова можно судить об устойчивости
автоматической системы как в замкнутом, так и в разомкнутом состоянии.
При критерии Найквиста устойчивость замкнутой системы исследуют по
частотной передаточной функции её разомкнутой системы, а эта функция чаще
всего состоит из простых сомножителей.
При использовании критериев Гурвица, Рауса и Михайлова для исследова-
ния устойчивости автоматической системы рассматривают её характеристиче-
ское уравнение. В ряде случаев трудоемкость расчетов можно уменьшить за
счет изменения масштаба коэффициентов этого уравнения.
После деления на
0
a
и замены переменной путем подстановки
,
λ
cp
=
где
постоянная
,0
>
c
характеристическое уравнение (5)принимает следующий вид
.01 )8(
0
1
1
0
1
1
0
=++++
−
−
−
λλλ
a
ca
a
ca
a
ca
n
n
n
n
n
n
Постоянную c следует выбирать так, чтобы коэффициент
1
0
=
a
ca
n
n
или был
близко к единице. Иногда удобнее это требование предъявлять к коэффициенту
0
1
a
ca
. В ряде случаев целесообразно принимать
.10
=
с
В результате характеристическое уравнение принимает более простой вид,
а его корни лишь уменьшаются в с раз.
Пример. Имеется характеристическое уравнение
.02505,8775,825,0
23
=+++
ppp
Его корни:
.20 ;10 ;5
321
−=−=−=
ppp
Разделим уравнение на
250
0
=
a
.0135,0035,0001,0
23
=+++
ppp
Сделаем подстановку
:10
λ
=
p
.015,35,3
23
=+++
λλλ
Уравнение приняло более простой вид. Его корни:
.2 ;1 ;5,0
321
−=−=−=
ppp
34
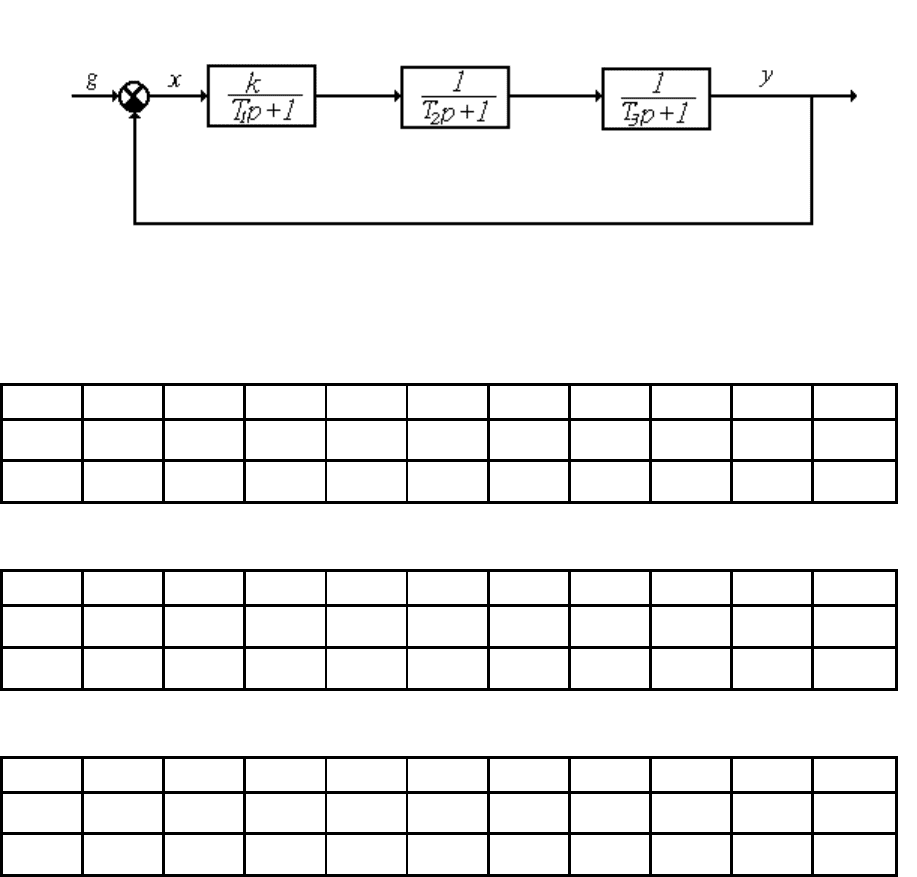
2.ИССЛЕДОВАНИЕ
В лабораторной работе исследуется автоматическая система, структурная
схема которой имеет вид
Варианты
№ 1 2 3 4 5 6 7 8 9 10
T
1
0,1 0,1 0,1 0,1 0,1 0,1 0,5 0,5 0,5 0,5
C
3
3 4 5 6 7 8 3 4 5 6
№ 11 12 13 14 15 16 17 18 19 20
T
1
0,5 0,5 1 1 1 1 1 1 2 2
C
3
7 8 3 4 5 6 7 8 3 4
№ 21 22 23 24 25 26 27 28 29 30
T
1
2 2 2 2 5 5 5 5 5 5
C
3
5 6 7 8 3 4 5 6 7 8
3. ЗАДАНИЕ
3.1.Используя критерий Гурвица, получите выражение, исходя из которого
можно сделать вывод, что устойчивость рассматриваемой системы зависит не
от абсолютных значений постоянных времени, а лишь от соотношения между
ними, т.е. выражение вида
),,(
32
CCkk
кркр
=
−
кр
k
значение коэффициента усиления, при котором автоматическая система
35

находится на границе устойчивости (при
−>
кр
kk
система неустойчива; при
−<
кр
kk
система устойчива); коэффициенты
2
C
и
3
C
соответственно равны
. ;
1
3
3
1
2
2
T
T
C
T
T
C
==
3.2.Постройте кривую
)(
2
Cfk
кр
=
при
constC
=
3
(величина С
3
задана),
которая разделяет области устойчивой и неустойчивой работы автоматической
системы.
3.3.Определите аналитически минимальное значение
.
min
кр
k
Это значение
можно определить, прибегая к исследованию на экстремум функции
)(
2
Cfk
кр
=
.
3.4.Заполните три таблицы Рауса для
,
min
кр
kk
>
,
min
кр
kk
<
min
кр
kk
=
для
заданной автоматической системы с заданными значениями
13
,TC
и значения
коэффициента
,
2
C
при котором было вычислено
.
min
кр
k
3.5.Постройте три кривых Михайлова для
,
min
кр
kk
>
k k
к
<
рmin
,
min
кр
kk
=
для заданной автоматической системы с заданными значениями
13
,TC
и значе-
ния коэффициента
,
2
C
при котором было вычислено
.
min
кр
k
3.6. В заданной автоматической системе разомкните обратную связь и для
получившейся разомкнутой системы постройте три АФЧХ для
,
min
кр
kk
>
,
min
кр
kk
<
min
кр
kk
=
для заданной автоматической системы с заданными значе-
ниями
13
,TC
и значения коэффициента
,
2
C
при котором было вычислено
.
min
кр
k
3.7.Путем моделирования получите три переходных функции для
,
min
кр
kk
>
,
min
кр
kk
<
min
кр
kk
=
для заданной автоматической системы с задан-
ными значениями
13
,TC
и значения коэффициента
,
2
C
при котором было вы-
числено
.
min
кр
k
3.8.Проанализируйте результаты моделирования с точки зрения связи ко-
эффициента усиления и устойчивости автоматической системы.
3.9.Покажите аналитически зависимость частоты колебаний от коэффици-
ента усиления.
4.СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА
4.1.Заданная структурная схема автоматической системы с заданными зна-
чениями параметров.
4.2.Вывод выражения и само выражение
).,(
32
CCkk
кркр
=
36

4.3.Построенная кривая
)(
2
Cfk
кр
=
при
constC
=
3
с отмеченными обла-
стями устойчивой и неустойчивой работы автоматической системы.
4.4.Определенное с помощью формулы
),(
32
CCkk
кркр
=
численное значе-
ние
.
min
кр
k
4.5.Три таблицы Рауса с необходимыми пояснениями процесса их фор-
мирования.
4.6.Три кривые Михайлова с необходимыми пояснениями процесса их по-
строения.
4.7.Три амплитудно-фазовые частотные характеристики разомкнутой авто-
матической системы.
4.8.Листинг фрагмента программы, относящегося к моделированию задан-
ной автоматической системы.
4.9.Результаты моделирования в удобной для анализа форме, т.е. графики
должны иметь обозначения, масштабы и т.п.
4.10.Анализ результатов моделирования с точки зрения связи коэффициен-
та усиления с устойчивостью автоматической системы.
4.11.Аналитическое доказательство зависимости частоты колебаний от ко-
эффициента усиления.
4.12.Текстовая часть отчета должна соответствовать ГОСТу 2.105-79, гра-
фики выполняются с учетом ГОСТа 2319-81, список использованной литерату-
ры осуществляется с учетом ГОСТа 7.1-81.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.В этой лабораторной работе при исследовании вопросов, связанных с
определением
min
кр
k
использовался критерий Гурвица. Предложите лаборатор-
ную работу № 3"А", в которой аналогичные вопросы исследуются с помощью
критерия Найквиста.
2.Найдите зависимость
),(
32
CCkk
кркр
=
, если вместо второго звена
1
1
)(
2
2
+
=
pT
pW
используется звено вида
.
1
)(
2
2
pT
pW
=
3.Проверить устойчивость замкнутой автоматической системы, если пере-
даточная функция разомкнутой системы имеет вид
.
)15(
110
)(
2
+
+
=
pp
p
pW
4.Определите предельный коэффициент усиления для автоматической си-
стемы, структурная схема которой представлена ниже. Здесь
.2,0 ;005,0
21
cTcT
==
37
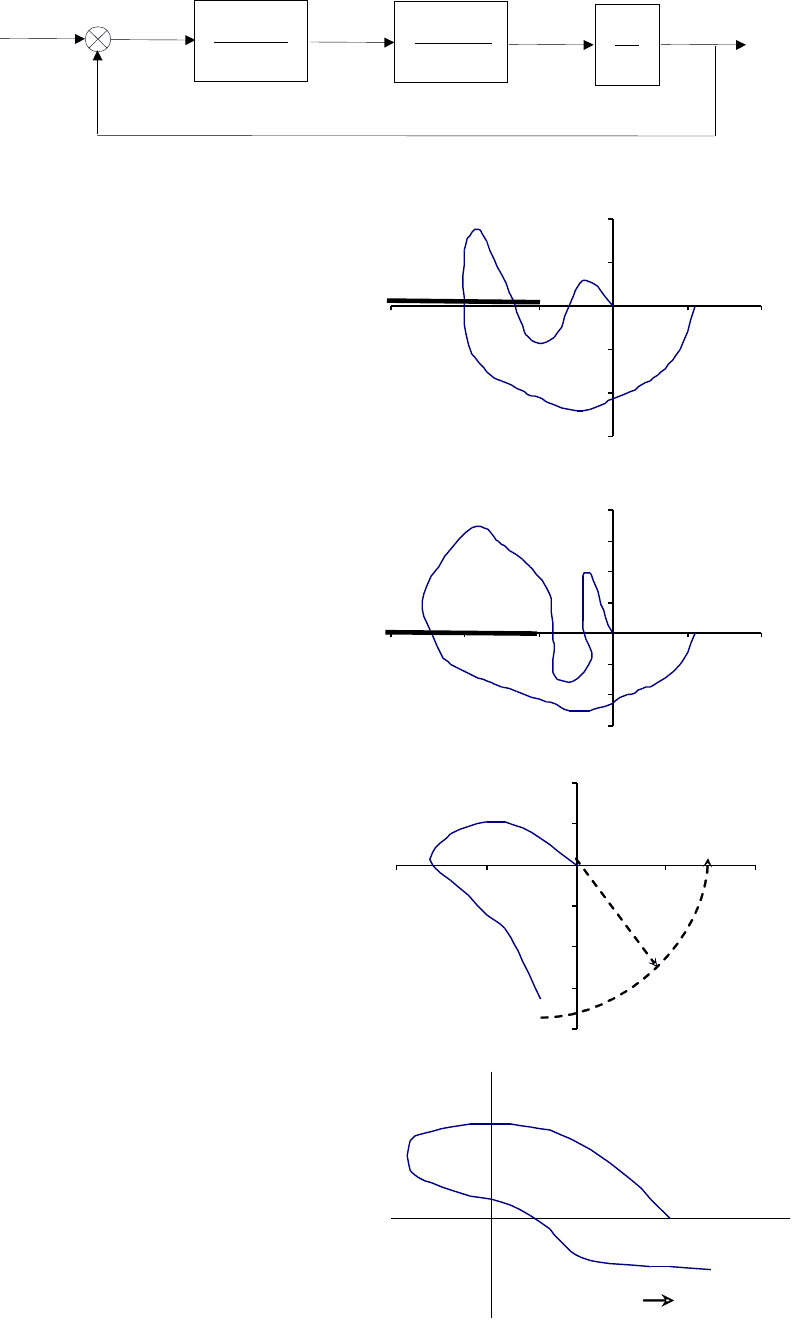
1
1
1
+
pT
k
p
k
3
1
2
2
+
pT
k
y(t)
g(t)
(-)
5.Дана амплитудно-фазовая ча-
стотная характеристика системы авто-
матического регулирования, имеющей
ноль полюсов в правой полуплоскости
у характеристического уравнения
разомкнутой системы. Проанализи-
руйте устойчивость автоматической
системы в замкнутом состоянии.
-1,5
-1
-0,5
0
0,5
1
-3 -2 -1 0 1 2
∞=
ω
Re
Im
0
=
ω
6.Дана амплитудно-фазовая ча-
стотная характеристика системы авто-
матического регулирования, имеющей
ноль полюсов в правой полуплоскости
у характеристического уравнения
разомкнутой системы. Проанализи-
руйте устойчивость автоматической
системы в замкнутом состоянии.
-1,5
-1
-0,5
0
0,5
1
1,5
2
-3 -2 -1 0 1 2
∞=
ω
Re
Im
0
=
ω
7.Дана амплитудно-фазовая ча-
стотная характеристика одноконтур-
ной системы автоматического регули-
рования, имеющей ноль полюсов в
правой полуплоскости у характеристи-
ческого уравнения разомкнутой систе-
мы. Проанализируйте устойчивость
автоматической системы в замкнутом
состоянии.
-1 -0,5 0 0,5 1
∞=
ω
Re
Im
0
=
ω
∞=
R
8.Приведена кривая Михайлова,
соответствующая неустойчивой систе-
ме. Определите число корней с поло-
жительной и отрицательной веще-
ственной частью, если известно, что
порядок характеристического полино-
ма этой автоматической системы рав-
но
.4
=
n
Re
Im
0
=
ω
∞=
ω
38
9.В одном из учебных пособий по "Теории автоматического управления"
студент Иванов И.И. прочитал такое.
Иногда может оказаться удобным следующий критерий устойчивости, на-
зываемый к р и т е р и е м п е р е м е ж а е м о с т и к о р н е й .
Пусть
).()()(
ωωω
jVUjD
+=
Тогда очевидно, что кривая
)(
ω
jD
при изменении
ω
от 0 до ∞ обходит
n
квадрантов в положительном направлении и автоматическая система устойчи-
ва, если
0)0( ,0)0(
>
′
>
VU
и уравнения
0)( **
,0)( *
=
=
ω
ω
V
U
имеют все действительные и перемежающиеся корни, т.е. если между каждыми
двумя соседними корнями уравнения (*) [или(**)] лежит корень уравнения (**)
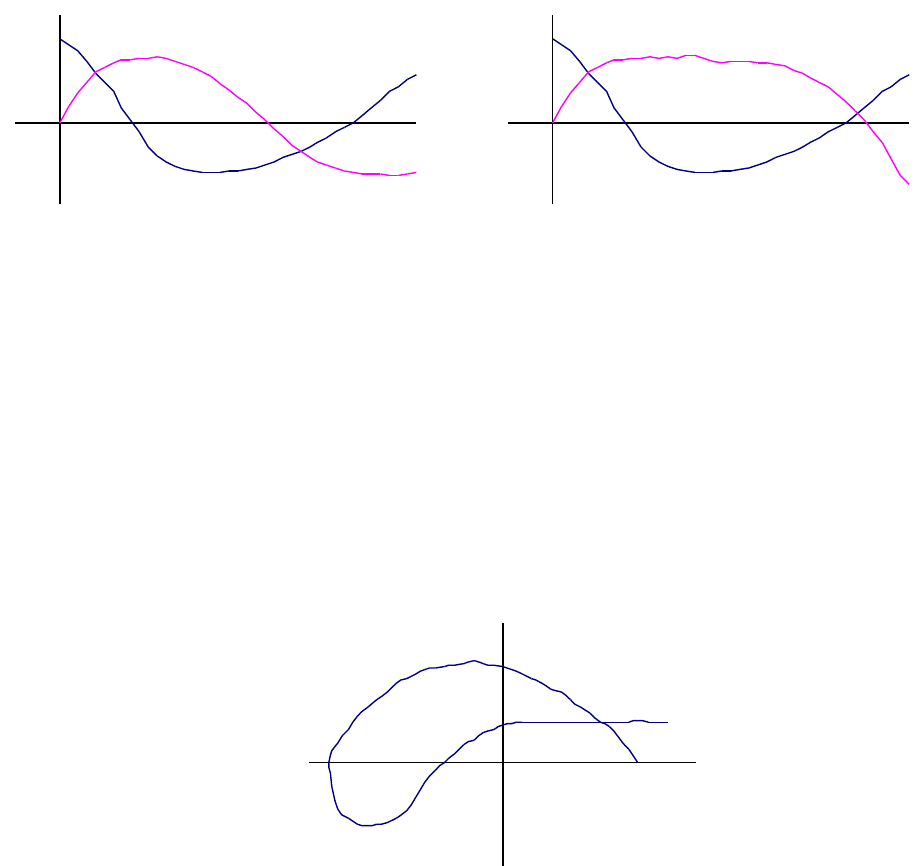
[или (*)]. Так, например, при
4
=
n
случай, изображенный на рис. 5 соответ-
ствует устойчивой системе, а на рис. 6 неустойчивой системе.
Рис. 5
.
ω
1
ω
2
ω
3
ω
)(
ω
U
)(
ω
V
UV,
)0(U
Рис. 6
.
ω
1
ω
2
ω
3
ω
)(
ω
U
)(
ω
V
UV,
)0(U
Оказалось, что вышесказанное для студента Иванова И.И. неочевидно.
Убедите все же его в том, что вышесказанное верно.
10.Автоматическая система имеет характеристическое уравнение пятого
порядка. Известно, что число корней с положительной вещественной частью
.2
=
m
Студент Иванов И.И. построил кривую Михайлова. Преподаватель, про-
веряя методику построения представленной кривой Михайлова, утверждает,
что она (кривая Михайлова) построена неверно, по крайней мере, на участке
.
∞=
ω
Разъясните студенту Иванову И.И., как мог преподаватель так скоро обна-
ружить неверное построение кривой Михайлова.
V
U
0
=
ω
∞=
ω
0
39

ЛАБОРАТОРНАЯ РАБОТА № 4
КАЧЕСТВО ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
Цель работы - ознакомление с показателями качества процессов, проте-
кающих в автоматических системах; принцип суперпозиции в линейных авто-
матических системах; астатизм автоматических систем; точки приложения
входных воздействий в автоматических системах.
1.ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Всякая реальная автоматическая система действует в разнообразных режи-
мах, которые отличаются значениями задающего воздействия и возмущения
или характером их изменения. Чем меньше значения имеет при этом рассогла-
сование, тем выше качество управления. Однако единую объективную число-
вую оценку качества управления весьма затруднительно, если не невозможно, и
по этой причине приходится применять частичные оценки отдельных наиболее
характерных режимов.
В настоящее время разработано большое число различных критериев каче-
ства автоматических систем, которые условно можно разбить на четыре груп-
пы.
К первой группе относятся критерии, которые в той или иной степени ис-
пользуют для оценки качества величину ошибки в различных типовых режи-
мах.
Ко второй группе относят критерии, которые определяют величину запаса
устойчивости, т.е. критерии, устанавливающие, насколько далеко от границы
устойчивости находится автоматическая система.
Почти всегда опасной для автоматической системы является колебатель-
ная граница устойчивости. Это определяется тем, что стремление повысить об-
щий коэффициент усиления, как правило, приводит к колебательной границе
устойчивости и затем – к возникновению незатухающих колебаний.
Третья группа критериев качества определяет так называемое быстродей-
ствие автоматических систем. Под быстродействием понимается быстрота
(скорость) реагирования автоматической системы на появление управляющих
и возмущающих воздействий. Наиболее просто быстродействие может оцени-
ваться по времени затухания переходного процесса.
К четвертой группе критериев качества относятся комплексные критерии,
дающие оценку некоторых обобщенных свойств, которые могут учитывать
точность, запас устойчивости и быстродействие. Обычно это делается при по-
40
