Красников И.В. Технические средства судовождения
Подождите немного. Документ загружается.

31
3.2 ОПРЕДЕЛЕНИЕ ДЕВИАЦИИ МАГНИТНОГО
КОМПАСА
При использовании магнитного компаса истинные направления
рассчитываются по формулам:
ИП = КП
МК
+ d +
δ
; ИК = КК
МК
+ d +
δ
(7)
Где:
ИК
- истинный курс, [
°
];
ИП
- истинный пеленг, [
°
];
КК
МК
- компасный курс по магнитному компасу, [
°
];
КП
МК
- компасный пеленг по магнитному компасу, [
°
];
d - магнитное склонение в районе плавания, [
°
];
δ
- девиация магнитного компаса, [
°
].
Из приведенных формул видно, что при использовании магнитного
компаса определение истинных направлений предполагает знание
магнитного склонения в районе плавания и величины девиации
магнитного компаса.
Магнитное склонение снимается с карты и приводится к году
плавания по формуле:
d = d
к
+
Δ
d (Д
т
– Д
к
) (8)
Где:
d - магнитное склонение, приведенное к году плавания, [
°
];
d
к
- магнитное склонение, снятое с карты, [
°
];
Δ
d - годовое изменение магнитного склонения, [
°
/год];
Д
т
- текущий год;
Д
к
- год приведения магнитного склонения, снятого с карты.
Девиация магнитного компаса определяется одним из способов:
а) определение девиации по непосредственным наблюдениям компасных
пеленгов:
− определение девиации по вееру створов;
− определение девиации по одному створу;
− определение девиации по отдаленному ориентиру;
− определение девиации по светилу;
− определение девиации по взаимным
пеленгам.
б) определение девиации по сличению курсов компасов:
− определение девиации по сличению курсов с главным
магнитным компасом;
− определение девиации по сличению курсов с гирокомпасом.

32
в) определение девиации по силам, измеренным дефлектором Колонга:
− определение девиации по силам на четырех компасных курсах;
− определение девиации по силам на восьми компасных курсах.
При выборе способа определение девиации необходимо учитывать,
что наилучшая точность достигается при определении девиации на ходу
судна по вееру створов и одному створу,
направление которых известно.
При определении девиации по пеленгам ошибка в наблюденной девиации
будет не более 0,2°, при определении девиации по сличению курсов
достигает 0,5°, при определении девиации по силам на восьми компасных
курсах – 0,5°, а на четырех компасных курсах – 1,0°.
Величину девиации магнитного компаса при непосредственном
наблюдении
компасных пеленгов определяется по
формуле:
δ
= ОМП – ОКП (9)
Где:
ОМП - обратный магнитный пеленг ориентира (створа);
ОКП - обратный компасный пеленг.
Обратный магнитный пеленг ориентира может быть определен по
результатам непосредственных измерений обратных пеленгов данного
ориентира на восьми компасных курсах по формуле:
8
NWWSWSSEENEN
ОКПОКПОКПОКПОКПОКПОКПОКП
ОМП
+
+
+
+
+
+
+
=
(10)
Где:
ОКП
N
, ОКП
NE
… - обратные компасные пеленга на ориентир,
измеренные на компасных курсах N, NE и т.д.
Судно ложится последовательно на главные и четвертные румбы по
магнитному компасу, после 2-3 минут лежания на курсе измеряется
обратный пеленг на ориентир. Магнитный пеленг рассчитывается по
формуле:
МП = ОМП
±
180
°
(11)
Наибольшее распространение в практике кораблевождения получил
способ определения девиации магнитного компаса по сличению с
гирокомпасом на восьми компасных курсах. При реализации данного
способа необходимо учитывать, что у гирокомпаса при выполнении
маневра возникают баллистические девиации, достигающие нескольких
33
градусов. Поэтому следует на время выполнения наблюдений отключить
масляный успокоитель, а маневрирование выполнять на малом ходу.
Значение девиации магнитного компаса по сличению с
гирокомпасом рассчитывается по формуле:
δ
= (КК
ГК
– КК
МК
) +
Δ
ГК – d (12)
Где:
КК
ГК
- компасный курс по гирокомпасу, [
°
];
Δ
ГК - поправка гирокомпаса, [
°
].
Оба эти способа связаны с непосредственными наблюдениями и,
потому, не желательны ввиду возможного наличия промахов в
наблюдениях. Для уменьшения погрешностей полученные результаты
используются для расчета приближенных коэффициентов девиации:
А = 1/8 (
δ
N
+
δ
S
+
δ
E
+
δ
W
+
δ
NE
+
δ
SE
+
δ
NW
+
δ
SW
);
В = 1/4 [(
δ
E
-
δ
W
) + (
δ
NE
+
δ
SE
-
δ
NW
-
δ
SW
) sin45
°
];
C = 1/4 [(
δ
N
-
δ
S
) + (
δ
NE
-
δ
SE
+
δ
NW
-
δ
SW
) sin45
°
]; (13)
D = 1/4 (
δ
NE
-
δ
SE
-
δ
NW
+
δ
SW
);
E = 1/4 (
δ
N
+
δ
S
-
δ
E
-
δ
W
).
Где:
А,…Е - приближенные коэффициенты девиации;
δ
N
,…
δ
SW
- значения девиации, полученные на соответствующих
курсах.
При расчете приближенных коэффициентов девиации случайные
погрешности, допущенные при наблюдениях, «разгоняются», и
рассчитанная по коэффициентам девиация становится более точной, чем
наблюденная.
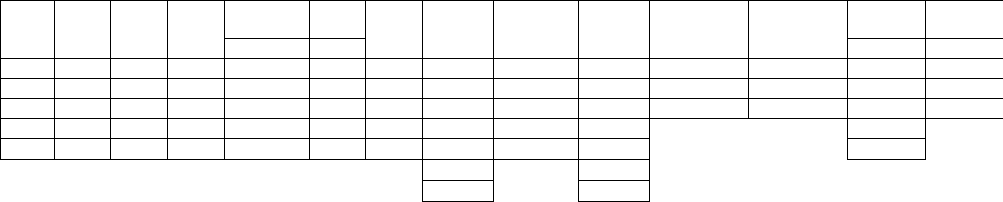
Для удобства вычисления коэффициентов девиации используется
Таблица 1. Все промежуточные расчеты производятся с точностью до
0,01°, а конечный результат округляется до 0,1 °.
Таблица 1.
Кмк
δ
Кмк
δ
I+II I-II
k k*IV k k*IV
верхняя
половина
графы III
нижняя
половина
графы III
VII+VII
I VII-VIII
2 2 2 2
I II III IV V VI VII VIII IX X
N S q
1
= 0 - 1 q
1
= q
3
= Е=
NE SW q
2
= 0.71 0.71 q
2
= q
4
= Д=
E W q
3
= 1 0 -
∑=
SE NW q
4
= 0.71 -0.71
А=∑/2=
∑=
∑=
В=∑/2=
С=∑/2
34
После получения коэффициентов девиации рассчитывается таблица
девиации. Значение девиации для произвольного курса может быть
рассчитано по точной формуле девиации:
sin
δ
= Acos
δ
+ BsinKK + CcosKK + Dsin(2KK +
δ
) + Ecos(2KK +
δ
) (14)
При девиации δ < 12,5° данная формула может быть упрощена:
δ
= A + BsinKK + CcosKK + Dsin(2KK) + Ecos(2KK) (15)
Данная формула известна как «Основная формула девиации».
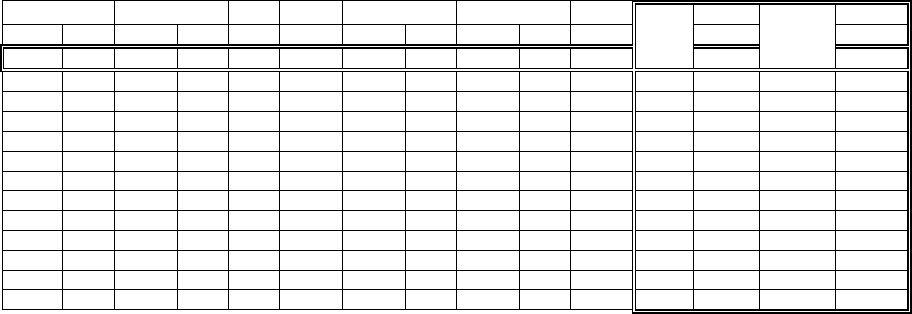
Именно эта формула используется для расчета таблицы девиации
(Таблица 2):
Таблица 2.
D = E = A = B = C =
KK
δ
KK
δ
m
1
Dm
1
m
2
m
2
E I+II III+A m
3
m
3
B m
4
m
4
C V+VI IV+VII IV-VII
I II III IV V VI VII VIII IX
0 1 0 - 1 0 180
0..5 0.87 0.26 0.97 15 195
0.87 0.5 0.5 0.87 30 210
1 0 - 0.71 0.71 45 225
0.87 -0.5 0.87 0.5 60 240
0..5 -0.87 0.97 0.26 75 255
0 -1 1 0 - 90 270
-0.5 -0.87 0.97 -0.26 105 285
-0.87 -0.5 0.87 -0.5 120 300
-1 0 - 0.71 -0.71 135 315
-0.87 0.5 0.5 -0.87 150 330
-0.5 0.87 0.26 -0.97 165 345
3.3 ЭКСПЛУАТАЦИОННЫХ ХАРАКТЕРИСТИК
ГИРОКОМПАСОВ
К эксплуатационным характеристикам гирокомпасов относятся
такие, как:
− период собственных незатухающих колебаний;
− период затухающих колебаний;
− фактор затухания;
− критическая широта и т.д.
Зная данные характеристики, можно судить о возможных
погрешностях и путях их определения и компенсации, о подверженности
курсоуказателей влиянию внешних факторов, о степени готовности
технических средств с
момента запуска и т.д.
3.3.1 ПЕРИОД НЕЗАТУХАЮЩИХ КОЛЕБАНИЙ, КРИТИЧЕСКАЯ
ШИРОТА ГИРОКОМПАСА
Главная ось гирокомпаса с отключенным масляным успокоителем
описывает в пространстве незатухающие колебания. Значение периода

35
собственных незатухающих колебаний является существенной характе-
ристикой, определяющей его точность в условиях маневрирования судна.
Исходя из стабильности периода собственных незатухающих колебаний,
гирокомпасы делятся на две группы:
− апериодические или регулируемые гирокомпасы;
− неапериодические или не регулируемые гирокомпасы.
К первой группе относится гирокомпас «Курс 5». В данном гиро-
компасе период собственных
незатухающих колебаний поддерживается
постоянным при изменении широты плавания. Это достигается путем
регулирования величины гироскопического момента чувствительного
элемента изменением угла разворота гироскопов.
Ко второй группе относятся гирокомпасы типа «Амур» и
«Курс 4(М)». В данных гирокомпасах величина периода собственных
незатухающих колебаний изменяется с широтой плавания.
Период собственных незатухающих колебаний гирокомпаса
рассчитывается по
формуле:
ϕω
π
cos
2
0
o
Г
B
H
T = (16)
Где:
Н
Г
- кинетический момент чувствительного элемента
гирокомпаса, [Нмс];
В - модуль маятникового момента чувствительного элемента
гирокомпаса, [Нм];
ω
о
- угловая скорость суточного вращения Земли, [7,29
.
10
-5
с
-
];
ϕ
- широта места, [
°
].
Период незатухающих колебаний гирокомпаса на подвижном
основании отличается от периода собственных незатухающих колебаний
последнего. И объясняется это различие влиянием на поведение
чувствительного элемента не только горизонтальной составляющей
суточного вращения Земли, но и параметров движения судна.
Расчет периода незатухающих колебаний гирокомпаса на
подвижном основании производится по формуле:
22
0
)()cos(
2
o
N
o
E
o
Г
R
V
R
V
B
H
T
++
=
ϕω
π
(17)
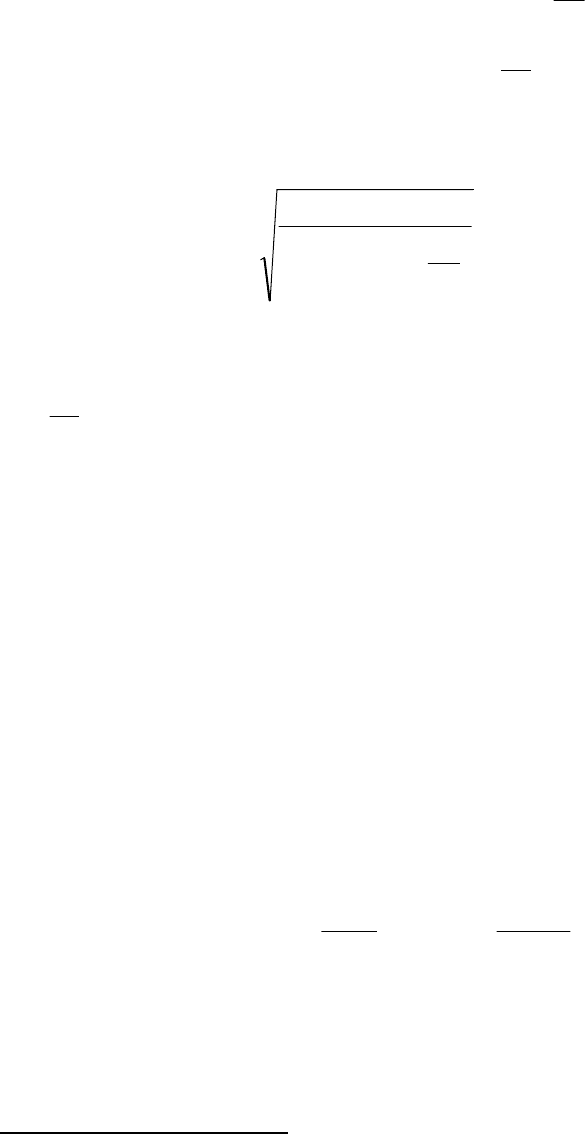
36
Где:
R
о
- радиус Земли, [6,37
.
10
6
м];
V
N
- меридиональная составляющая линейной скорости судна,
[м/с];
V
Е
- восточная составляющая линейной скорости судна, [м/с].
При решении практических задач кораблевождения в средних
широтах и на небольших скоростях величиной
o
N
R
V
можно пренебречь
ввиду ее малости по сравнению с (
ω
о
cos
ϕ
+
o
E
R
V
) . В этом случае расчет
периода незатухающих колебаний можно производить по формуле:
)cos(
2
0
o
E
o
Г
R
V
B
H
T
+
=
ϕω
π
(18)
Из анализа формулы (17) видно, что при выполнении равенства
0cos =+
o
E
o
R
V
ϕω
, период незатухающих колебаний гирокомпаса стремится
к бесконечности. А это значит, что если главная ось чувствительного
элемента будет выведена из положения равновесия внешней силой, то
она в это положение уже не возвратится. Запишем последнее выражение
в следующем виде:
ω
о
R
o
cos
ϕ
= - V
E
(19)
Левая часть данного равенства характеризует линейную скорость
точки на поверхности Земли в данной широте. Данная скорость
направлена с Запада на Восток. При движении судна курсом 270° (с
Востока на Запад) с аналогичной скоростью гирокомпас прекратит
работу. Из формулы (19) видно, что каждой восточной составляющей
скорости судна будет соответствовать своя критическая широта
ϕ
кр
(широта на которой гирокомпас прекращает функционировать):
)
900
sin
arccos()arccos(
КV
R
V
oo
E
КР
−=−=
ω
ϕ
(20)
Где:
V – скорость судна, [узл];
К – курс судна, [
°
].
1
1
При строгом решении задачи под курсом понимается путевой угол судна с учетом
дрейфа и течения.
37
3.3.2 ПЕРИОД ЗАТУХАЮЩИХ КОЛЕБАНИЙ
Для превращения незатухающих колебаний главной оси
чувствительного элемента в затухающие в гирокомпасах типа «Курс»
используются гидравлические (масляные) успокоители. При наличии
включенного масляного успокоителя движение главной оси гирокомпаса
описывается формулой:
α
= А
1
е
– mt
+ е
– nt
(B
1
cos
ω
d
t + C
1
sin
ω
d
t) (21)
Где:
А
1
, В
1
, С
1
– произвольные постоянные интегрирования,
определяемые начальными условиями;
ω
d
– круговая частота затухающих колебаний, [c
-1
];
m, t – коэффициенты Рауса – Гурвица, [c
-1
].
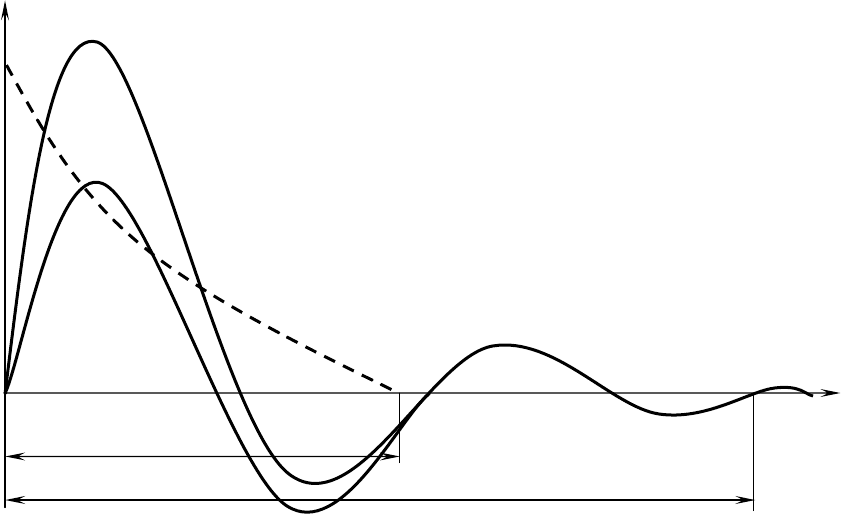
В общем случае кривая затухающих колебаний имеет вид
приведенный на рисунке (Рис. 1).
Рис. 1
Формула (21) состоит из двух слагаемых, первое из которых
отображает апериодическое движение и определяется выражением
А
1
е
– mt
0
α
t
1
А
1
е
-mt
t
t
2
α
= А
1
е
–
mt
+ е
–
nt
(B
1
cos
ω
d
t + C
1
sin
ω
d
t)
е
–
nt
(B
1
cos
ω
d
t + C
1
sin
ω
d
t)

38
Для определения времени затухания апериодической составляющей
t
1
условно считаем, что колебания затухают при уменьшении
первоначальной их величины в 100 раз, т.е.
А
1
/ 100 = А
1
е
– mt
(22)
Из формулы (22) получим:
T
1
= ln100 / m
≈
85 мин (23)
Таким образом, апериодическая составляющая через 1,5 часа после
пуска гирокомпаса равна нулю.
Второе слагаемое правой части формулы (21) имеет колебательный
характер с уменьшающейся амплитудой.
Апериодическое движение и периодические колебания в первые 1,5
часа накладываются друг на друга и образуют сложную кривую
затухающих колебаний. В остальное время происходят гармонические
колебания, и главная ось
гиросферы приходит в положение равновесия.
Время полного затухания гармонических колебаний, в течение которого
амплитуда колебаний уменьшится в 100 раз, определяется формулой:
5,4
100ln
2
≈=
n
t часа (24)
Следовательно, при любом начальном отклонении главной оси
чувствительного элемента от меридиана затухание колебаний
практически произойдет через 4,5 часа. Период затухающих колебаний Т
d
зависит от параметров гиросферы и широты плавания.
Для гирокомпаса «Курс 4», обладающего следующими параметрами
Н
Г
= 15,55 Нмс; В = 0,657 Нм;
С = 0,399 Нм; τ
rm
= 666,7 сτ,
значения коэффициентов Рауса – Гурвица, периодов затухающих и не
затухающих колебаний в различных широтах плавания приведены в
Таблице 3:
Таблица 3.
Параметр
ϕ°
0 30 40 50 60 70 75 80
m
*
10
4
, [c
-1
] 7,068 7,328 7,589 8,035 8,888 10,416 11,72 12,82
n
*
10
4
, [c
-1
] 3,906 3,782 3,646 6,422 3,001 2,232 1,642 1,088
ω
d
*
10
4
, [c
-1
]
1,539 1,402 1,294 1,144 0,956 0,732 0,602 0,475
Т
d
, [мин] 68,0 74,7 80,9 91,5 109,5 142,9 174,0 220,3
Т
0
, [мин] 59,7 64,2 68,2 74,5 84,4 102,2 117,5 143,4
А
1
[° / узл]
- 0,019 - 0,026 - 0,035 - 0,051 - 0,081 - 0,121 - 0,130 - 0,132
А
2
[° / узл]
- 0,044 - 0,027 - 0,009 +0,023 +0,081 +0,181 +0,251 +0,374
А
3
[° / узл]
+0,055 +0,061 +0,066 +0,071 +0,070 +0,037 +0,003 - 0,034
39
Интенсивность затухания характеризуется фактором затухания –
уменьшением амплитуды колебаний за половину периода.
Числено фактор затухания f равен отношению предыдущего
максимального отклонения главной оси чувствительного элемента
гирокомпаса к последующему максимальному отклонению в
противоположную сторону.
Измерения производятся при установившемся движении (т.е. через
1,5 часа после включения режима «с затуханием» (пуска) гирокомпаса).
Для
определения фактора затухания принято исключать из
рассмотрения начальную часть кривой (примерно 60-80 минут),
поскольку на этом участке колебания чувствительного элемента имеют
неустановившийся характер. Отбрасывается также последний участок
(примерно 40-50 минут), так как вследствие уже малых амплитуд
колебаний трудно точно определить значение полупериода колебаний.
Используя оставшийся участок кривой, снимают значение величины
Т
d
и находят значение фактора затухания по формулам:
f
1
=
α
1
/
α
2
; f
2
=
α
2
/
α
3
; f
ср
= (f
1
+ f
2
) / 2 (25)
В заводском описании каждого гирокомпаса помещена таблица
стандартных значений периода затухающих колебаний в различных
широтах с допуском ±15 минут, а также допустимые значения фактора
затухания. Если полученные опытным путем значения периода
затухающих колебаний и фактора затухания не соответствуют табличным
в широте проведения испытаний с учетом допусков, то чувствительный
элемент подлежит
немедленной замене.
3.3.3. ОПРЕДЕЛЕНИЕ ЭКСПЛУАТАЦИОННЫХ
ХАРАКТЕРИСТИК ГИРОКОМПАСА
Практическое определение периодов затухающих и незатухающих
колебаний чувствительного элемента гирокомпаса выполняется на
поверочном стенде или при стоянке судна у стенки. Измерения
производятся последовательно. С этой целью необходимо:
а) определение периода незатухающих колебаний
−
привести гирокомпас в меридиан (4,5 – 6 часов);
−
выставить перо курсографа на середину ленты (Рис. 2, точка 1);
−
перевести гирокомпас в режим «без затухания»;
−
включив схему ускоренного приведения чувствительного
элемента в меридиан, добиться отклонения чувствительного
элемента от положения равновесия на 30° (точка 2) и отключить
схему ускоренного приведения;
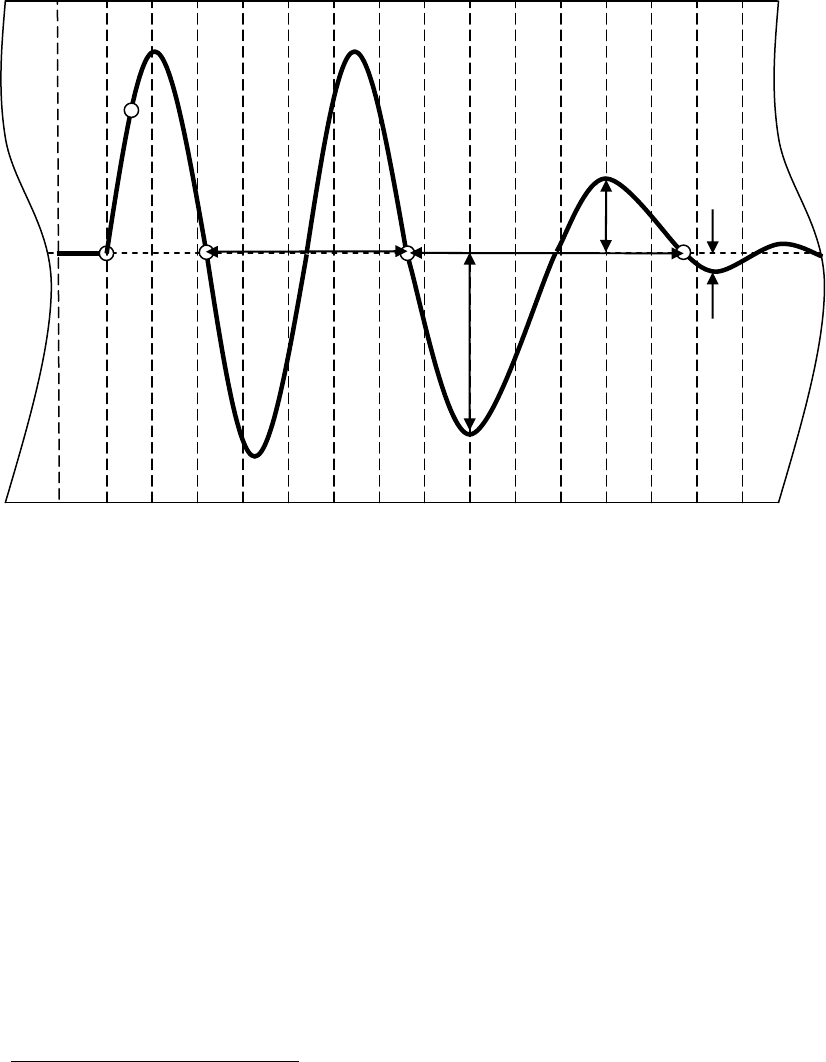
40
−
в момент пересечения пером средней линии (точка 3) запустить
секундомер
2
;
−
по завершению полного периода незатухающих колебаний
(точка 4) остановить секундомер. Полученное время – период
незатухающих колебаний Т
0
.
Рис. 2
а) определение периода затухающих колебаний и фактора затухания
−
в точке 4 перевести гирокомпас в режим «с затуханием» и
запустить секундомер;
−
по завершению полного периода затухающих колебаний (точка
5) остановить секундомер. Полученное время – период
затухающих колебаний Т
d
;
−
снять с графика максимальные отклонения пера курсографа от
центральной линии (α
1
, α
2
и α
3
) и рассчитать по формуле (25)
значение фактора затухания
3
.
Сравнить полученные результаты с табличными и сделать вывод о
работоспособности чувствительного элемента.
2
Интервалы времени могут измеряться с использованием шкалы, нанесенной на ленте
курсографа. В этом случае следует производить осреднение серии измерений, расположенных
симметрично относительно средней линии.
3
При использовании предложенной методики последовательного определения
периодов незатухающий и затухающих колебаний требования, изложенные в параграфе 1.3.2
с порядку определения фактора затухания, могут не выполняться.
1
Т
0
Т
d
5
4
3
2
α
1
α
2
α
3
