Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи
Подождите немного. Документ загружается.

§1.22. Задачи алгебры с использованием геометрии 141
Задача 289 (физический факультет (март), 1997, № 8). В треуголь-
ной пирамиде SKLM угол KLM прямой, SK = 5, SL = 6, SM = 7.
Найдите расстояние от вершины S до такой точки N, что KLMN —
прямоугольник.
Задача 290 (географический факультет (июль), 1996, № 4 (5)).
Углы треугольника ABC удовлетворяют равенству
cos
2
α + cos
2
β + cos
2
γ = 1.
Найдите площад ь треугольника, если радиусы вписанной и описанной
окружностей равны
√
3 и 3
√
2 соответственно.
Задача 291 (химический факультет (июль), 1997, № 5). Площадь
треугольника ABC равна 10 см
2
. Какое наименьшее значение может
принимать длина окружности, описанной около треугольника ABC,
если известно, что середины высот этого треугольника лежат на одной
прямой?
Задача 292 (химический факультет (июль), 1999, № 5). В сферу
радиуса 1 вписан параллелепипед, объём которого равен 8
√
3/9. Най-
дите площадь полной поверхности параллелепипеда.
Задача 293 (экономический факультет (отделение экономики)
(июль), 2001, № 6 (7)). Центры двенадцати шаров равных радиусов
совпадают с середи нами рёбер правильной шестиугольной пирамиды.
Найдите величин у двугранного угла при ребре основания пирамиды,
если известно, что шар, вписанный в пирамиду, касается всех двена-
дцати данных шаров.
Ответы. 288. 15/2. 289.
√
38. 290. 6
√
6 + 3. 291. 2π
√
10 см. 292. 8.
293. arccos(6 −
√
33).
§1.22. Задачи алгебры
с использованием геометрии
Пример 54 (заочная олимпиада в МГУ «Покори Воробьёвы горы»
2005, № 8 (10)). Найдите наименьшее значение выражения
p
(x − 9)
2
+ 4 +
p
x
2
+ y
2
+
p
(y − 3)
2
+ 9.
142 Часть 1. Основные задачи и методы их решения
x
y
O
5
3
12
C(12, 5)
d
1
d
2
d
3
A(x; y)
B(x + 3; 3)
Рис. 1.84
x
y
O
5
3
12
C(12, 5)
d
1
d
2
d
3
A(21/5; 7/4)
B(36/5; 3)
Рис. 1.85
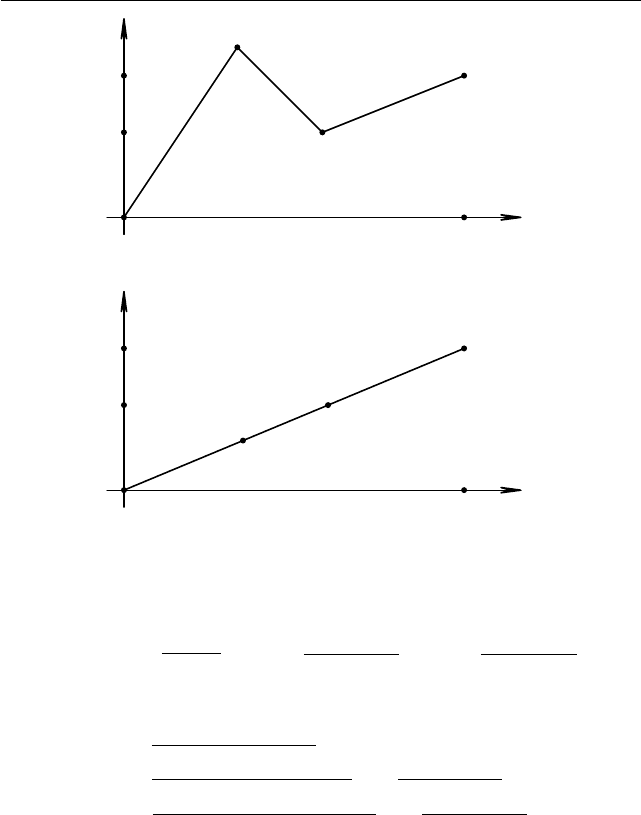
Решение. Данный пример можно решать при помощи производ-
ной, но наиболее простое решение следующее. Достаточно взглянуть
на картинки (см. рис. 1.84, 1.85):
Пусть d
1
=
p
x
2
+y
2
, d
2
=
p
(y −3)
2
+9, d
3
=
p
(x−9)
2
+4, точка
O(0; 0) — начало координат. Исходное выражение есть сумма расстоя-
ний между тремя точками A(x; y), B(x+3; 3), C(12; 5). Действительно,
|OA| =
p
(x − 0)
2
+ (y − 0)
2
= d
1
,
|AB| =
p
(x + 3 − x)
2
+ (3 − y)
2
=
p
(y − 3)
2
+ 9 = d
2
,
|BC| =
p
(12 − (x + 3))
2
+ (5 − 3)
2
=
p
(x − 9)
2
+ 4 = d
3
.
Следовательно, наименьшее значение суммы р асстояний d
1
, d
2
, d
3
бу-
дет достигаться, если точки A и B окажутся на одном отрезке, соеди-
няющем точки O и C (см. рис. 1.85).
Проверим, что такое расположение точек возможно. Уравнение пря-
мой, пр оходящей через точки O и C имеет вид x/12 = y/5, но, по-
скольку данная прямая должна проходить через точку B(x + 3; 3), мы
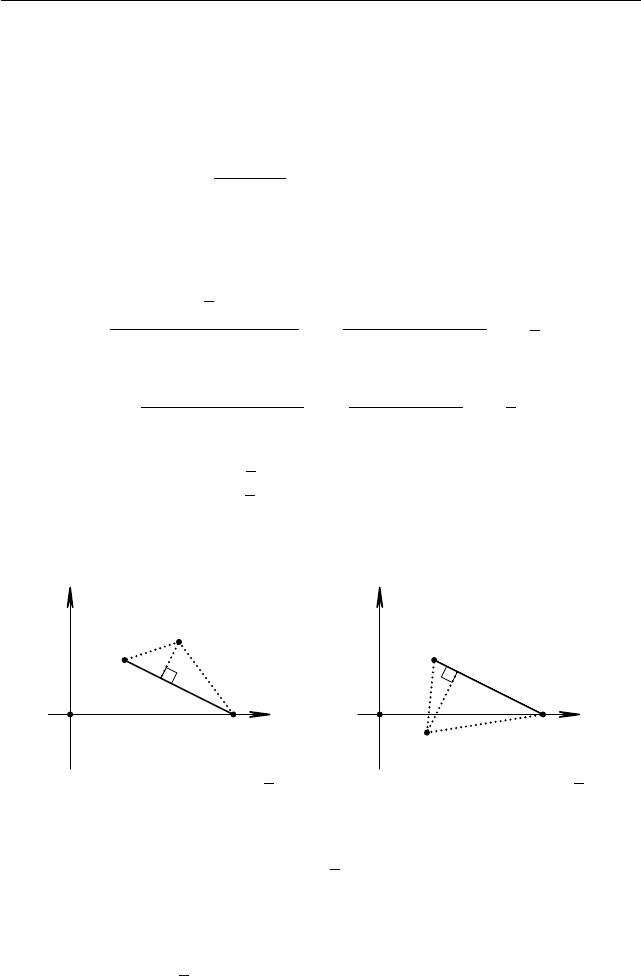
§1.22. Задачи алгебры с использованием геометрии 143
приходим к с исте ме
(
x/12 = y/5,
(x + 3)/12 = 3/5
⇐⇒
(
x = 21/5,
y = 7/4.
Таким образом, н ами доказано, что расположение, когда все точки
находятся на одной прямой, возможно. Следовательно, наим ен ьшее
значение выражения
√
12
2
+ 5
2
= 13.
Ответ. 13.
Пример 55 (геологическ ий факультет (май), 2003, № 7). Решите
систему уравнений
(
2
1+x
= 32y
√
2,
p
x
2
+ y
2
+ 2 − 2x − 2y +
p
x
2
+ y
2
− 6x + 9 =
√
5.
Решение. Исследуем второе уравнение. Запишем его в виде
p
(x − 1)
2
+ (y − 1)
2
+
p
(x − 3)
2
+ y
2
=
√
5.
Данное уравнение означает, что сумма расстояний от точки (x; y) до
точек (1; 1) и (3; 0) равна
√
5. Но поскольку расстояние между точками
(1; 1) и (3; 0) тоже равно
√
5, это означает, что точка (x; y) должна ле-
жать на отрезке, соединяющем вершины точек (1; 1) и (3; 0) см. рисун-
ки. Или, други ми словами, должно выполняться уравнение y = (3 −x)/2
x
y
0
(3; 0)
(1; 1)
(x; y)
d
1
d
2
x
y
0
(3; 0)
(1; 1)
(x; y)
d
1
d
2
Рис. 1.86. d
1
+ d
2
>
√
5 Рис. 1.87. d
1
+ d
2
>
√
5
для x ∈ [1; 3]. Таким образом, исходная систем а равносильна сис теме
(
2
1+x
= 32y
√
2,
2y = 3 − x, x ∈ [1; 3].
Подставив 2y в первое уравнение, получаем
2
1+x
= 16(3 − x)
√
2 ⇐⇒ 2
x−7/2
= 3 − x ⇐⇒ 2
x−7/2
+ x = 3.
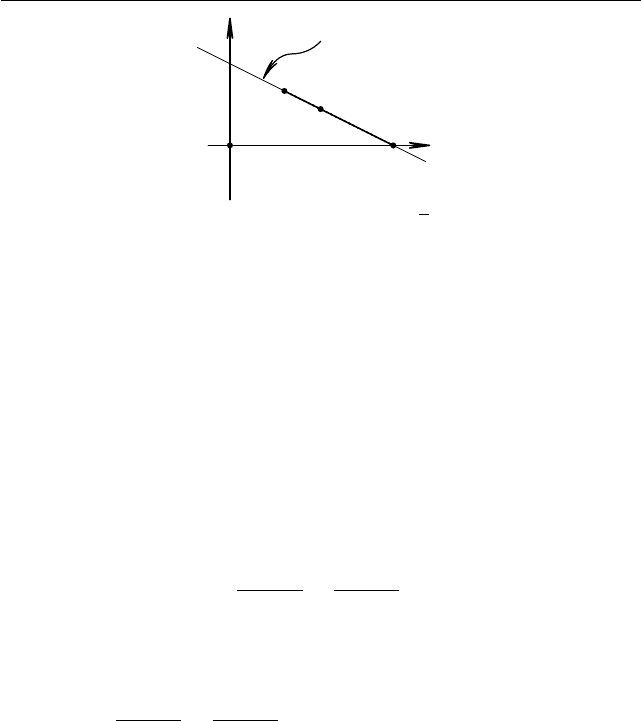
144 Часть 1. Основные задачи и методы их решения
x
y
0
(3; 0)
(1; 1)
(x; y)
d
1
d
2
y = (3 − x)/2
Рис. 1.88. d
1
+ d
2
=
√
5
Поскольку функция 2
x−7/2
+ x монотонно возрастающая (как сумма
двух монотонно возрастающих), каждое значение она принимает ров-
но один раз, см. §1.18. Поэтому решение x = 5/2 единственно.
Ответ. x = 5/2, y = 1/4.
Пример 56 (психологический факультет (июль), 1997, № 6 (6)).
Найдите все значения параметров a и b, при которых система уравне-
ний
(
x
2
+ y
2
+ 5 = b
2
+ 2x − 4y,
x
2
+ (12 − 2a)x + y
2
= 2ay + 12a − 2a
2
− 27
имеет два решения (x
1
; y
1
) и (x
2
; y
2
), удовлетворяющие условию
x
1
− x
2
y
2
− y
1
=
y
1
+ y
2
x
1
+ x
2
.
Решение. Последнее условие равноси льно тому, что два решения
лежат на окружности с центром в точке (0; 0), так как
x
1
− x
2
y
2
− y
1
=
y
1
+ y
2
x
1
+ x
2
⇐⇒ x
2
1
+ y
2
1
= x
2
2
+ y
2
2
.
Выделив полные квадраты, перепишем исходную систему в следую-
щем виде:
(
(x − 1)
2
+ (y + 2)
2
= b
2
,
(x + (6 − a))
2
+ (y − a)
2
= 9.
Эти уравнения задают окружности с центрами в точках O
1
(1; 2) и
O
2
(a − 6; a). Таким образом, координаты точек M
1
(x
1
; y
1
) и M
2
(x
2
; y
2
)
должны удовлетворять уравнениям сразу трёх окружностей.
Рассмотрим сначала окружности с центрами в точках O
1
(1; −2) и
O(0; 0). Так как M
1
M
2
— серединный перпендикуляр к OO
1
, точки
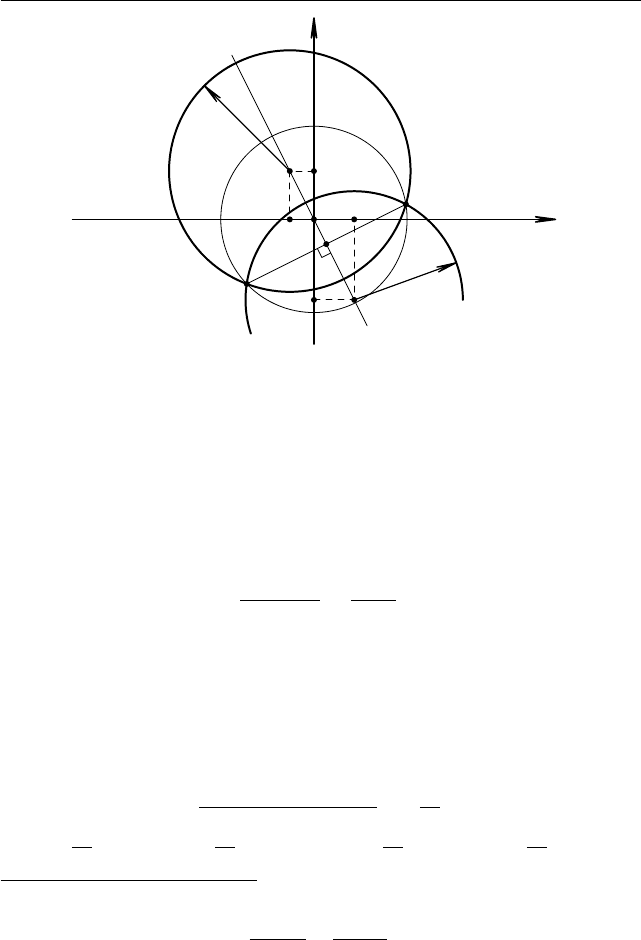
§1.22. Задачи алгебры с использованием геометрии 145
x
y
N
O
1
O
2
|b|
3
M
2
(x
2
; y
2
)
M
1
(x
1
; y
1
)
a
a − 6
1
−2
Рис. 1.89
O, N, O
1
лежат на одной прямой (N — точка пересечения M
1
M
2
с
OO
1
), перпендикулярной к M
1
M
2
. Аналогично, рассмотрев окр ужно-
сти с центрами в точках O
2
(a − 6; a) и O(0; 0), выводим, что точки O,
N, O
2
лежат на одной прямой, перпенд ик улярной к M
1
M
2
.
Таким образом, точки O, O
1
, O
2
лежат на одной прямой, проходя-
щей через точку N. Напишем уравнение прямой
1
, проходящей через
точки O
1
и O
2
:
x − 1
a − 6 − 1
=
y + 2
a + 2
.
Подставляя в уравнение прямой координаты точки O(0; 0), получаем
(−1)(a + 2) = 2(a − 7) ⇐⇒ 3a = 12 ⇐⇒ a = 4.
Окружности с центрами в точках O
1
и O
2
пересекаются в двух точках
тогда и только тогда, когда выполняются условия
O
1
O
2
− R
2
< R
1
< O
1
O
2
+ R
2
, ⇐⇒ O
1
O
2
− |b| < 3 < O
1
O
2
+ |b|.
Поскольку O
1
O
2
=
p
(1 + 2)
2
+ (−2 − 4)
2
=
√
45, мы получаем
√
45 − |b| < 3 <
√
45 + |b| ⇐⇒
√
45 − 3 < |b| <
√
45 + 3.
1
Уравнение прямой, проходящей через две заданные точки (x
1
, y
1
), (x
2
, y
2
), за-
писывается в виде
x − x
1
x
2
− x
1
=
y − y
1
y
2
− y
1
.
В случае x
2
= x
1
уравнение прямой имеет вид x = x
1
, а в случае y
2
= y
1
— вид
y = y
1
.

146 Часть 1. Основные задачи и методы их решения
Ответ. a = 4,
√
45 − 3 < |b| <
√
45 + 3.
Пример 57 (биологический факультет и факультет фундамен-
тальной м еди ци ны, 1992, № 5 (5)). Найдите наименьшее значение ве-
личины
1
c
·
3a
√
1 − u
2
+
b
√
1 − t
2
,
где a, b, c, t, u — положительные числа, удовлетворяющие условиям
at + bu 6 c,
a
2
+ 2bcu > b
2
+ c
2
,
b
2
·
t
2
− u
2
t
2
− 1
+ c
2
6 2bcu.
Решение. Так как 0 < u, t < 1, удобно сделать замену
u = cos α, t = cos β, α, β ∈ (0; π/2).
Тогда задача перепишется в следующем виде.
Найдите наименьшее значение величины
W =
1
c
·
3a
sin α
+
b
sin β
,
где a, b, c — положительные числа, а α, β ∈ (0; π/2) удовлетворяют
условиям
a cos β + b cos α 6 c, (1.16)
a
2
> b
2
+ c
2
− 2bc cos α, (1.17)
b
2
+ c
2
− 2bc cos α 6 b
2
sin
2
α
sin
2
β
. (1.18)
Докажем, что существует треугольник ABC со сторонами a, b, c и
углами α, β. Зададим треугольник ABC по сторонам b, c и углу между
ними α. Тогда оставшиеся сторона BC = a
0
и угол ∠ABC = β
0
заданы
однозначно.
Покажем, что при заданных условиях (1.16)–(1.18) справедливо ра-
венство a = a
0
, β = β
0
. Покаже м сначала, что угол β
0
острый. Пусть
угол β
0
тупой или прямоугольный, тогда проекция стороны AC на сто-
рону AB равна b cos α > c (см. рис. 1.91), что противоречит условию
(1.16). Следовательно, угол β
0
острый, т. е. β
0
∈ (0; π/2). Из теоремы
косинусов для треугольни ка ABC находим
a
2
0
= b
2
+ c
2
− 2bc cos α. (1.19)
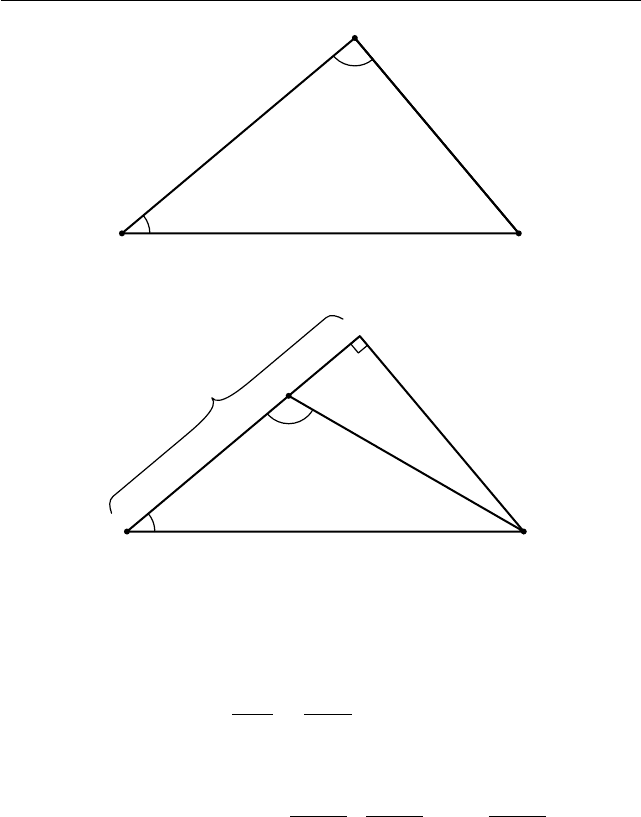
§1.22. Задачи алгебры с использованием геометрии 147
A C
b
c
a
0
α
β
0
B
Рис. 1.90. Треугольник ABC
A C
b
c
a
0
α
β
0
b cos α
B
Рис. 1.91. Случай тупого угла β
0
Из условия (1.17) делаем вывод: a > a
0
. Из теоремы синусов для тре -
угольника ABC получаем
a
0
sin α
=
b
sin β
0
= 2R.
Отсюда получаем
a
2
0
= b
2
+ c
2
− 2bc cos α 6 b
2
·
sin
2
α
sin
2
β
0
·
sin
2
β
0
sin
2
β
= a
2
0
·
sin
2
β
0
sin
2
β
⇐⇒
⇐⇒ sin
2
β 6 sin
2
β
0
⇐⇒ β 6 β
0
.
В последнем неравенстве мы воспользовались тем, что углы β, β
0
острые. Теперь из формулы (1.16) и соотношения a
0
cos β
0
+ b cos α = c
(сумма проекций сторон a
0
, b равна стороне c, см. рис. 1.92) получаем
c 6 a cos β + b cos α 6 a
0
cos β + b cos α 6 a
0
cos β
0
+ b cos α = c.
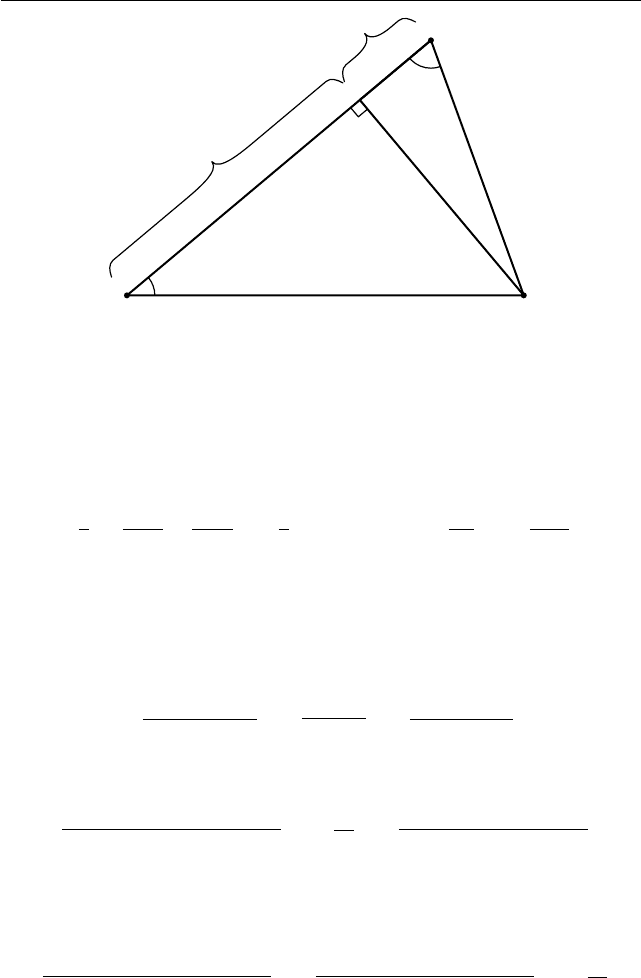
148 Часть 1. Основные задачи и методы их решения
A C
b
c
a
0
α
β
0
b cos α
a
0
cos β
0
B
Рис. 1.92. Треугольник ABC
Поскольку c = c, в каждом переходе должен быть знак равенства,
т. е. β = β
0
, a = a
0
. Таким образом, мы доказали, что существует тре-
угольник ABC со сторонами a, b, c и углами α, β. Используя теорему
синусов в треугольнике ABC, получаем
W =
1
c
·
3a
sin α
+
b
sin β
=
1
c
· (3 · 2R + 2R) =
8R
c
= 4 ·
1
sin γ
> 4.
Отметим, что знак равенства W = 4 достигается лишь в случае пря-
мого угла γ.
Ответ. 4.
Задача 294 (заочная олимпиада в МГУ «Покори Воробьёвы горы»
2005, № 8 (10)). Найдите наименьшее значение выражения
p
(x − 6)
2
+ 36 +
p
x
2
+ y
2
+
p
(y − 6)
2
+ 9.
Задача 295 (биологический факультет (июль), 2005, № 6 (7)). Ре-
шите систему
(
p
x
2
+ y
2
− 2x − 22y + 122 = 2
√
37 −
p
x
2
+ y
2
+ 2x + 2y + 2,
log
x+1
4 + log
y
4 = 0.
Задача 296 (факультет ВМиК (июль), 1996, № 5). Решите систему
(
x
2
+ y
2
− 14x − 10y + 58 = 0,
p
x
2
+ y
2
− 16x − 12y + 100 +
p
x
2
+ y
2
+ 4x − 20y + 104 = 2
√
29.

§1.22. Задачи алгебры с использованием геометрии 149
Задача 297 (геологический факультет (май), 2003, № 7). Решите
систему
(
2
2−x
= 4y
√
2,
p
x
2
+ y
2
+ 1 − 2x +
p
x
2
+ y
2
− 6x − 2y + 10 =
√
5.
Задача 298 (географический факультет (май), 1999, № 5). При
каких значениях параметра a система
(
y
2
− (2a + 1)y + a
2
+ a − 2 = 0,
p
(x − a)
2
+ y
2
+
p
(x − a)
2
+ (y − 3)
2
= 3
имеет единственное решение?
Задача 299 (психологический факультет (июль), 1997, № 6 (6)).
Найдите все действительные значения параметров a и b, пр и которых
система уравнений
(
x
2
+ 40 − a
2
= 4y − y
2
− 12x,
x
2
+ y
2
+ (−2b − 8)x = 2by − 2b
2
− 8b
имеет два решения (x
1
; y
1
) и (x
2
; y
2
), удовлетворяющие условию
y
1
+ y
2
x
1
− x
2
=
x
1
+ x
2
y
2
− y
1
.
Задача 300 (биологический факультет и факультет фундамен-
тальной м еди ци ны, 1992, № 5 (5)). Найдите наименьшее значение ве-
личины
1
r
·
4p
u
+
q
√
1 − v
2
,
где p, q, r, u, v — положительные числа, удовлетворяющие условиям
pv + q
p
1 − u
2
6 r,
p
2
+ 2qr
p
1 − u
2
> q
2
+ r
2
,
2qr
p
1 − u
2
+ q
2
·
1 − v
2
− u
2
v
2
− 1
> r
2
.
Ответы. 294. 15. 295. x = −1/2, y = 2. 296. x = (217 − 5
√
415)/29,
y = (180 + 2
√
415)/29. 297. x = 3/2, y = 1/4. 298. a ∈ [−2; 1) ∪ (1; 4].
299. b = −1,
√
90 − 4 < |a| <
√
90 + 4. 300. 5.

Часть 2
Варианты вступительных экзаменов
§2.1. Варианты 2003 года
ВАРИАНТ 2003 (март), механико-математический
факультет, 1.
Задача 1. Найдите первый член целочисленной арифметической
прогрессии, у которой сумма первых шести членов отличается от сум-
мы следующих шести членов мен ее чем на 450, а сумма первых пяти
членов превышает более чем на 5 сумму любого другого набора раз-
личных членов этой прогрессии.
Задача 2. Решите неравенство
r
4x
7
− 10x
3
4x − x
3
− 3
6 x
3
.
Задача 3. На продолжении биссектрисы AL тре угольника ABC
за точку A взята такая точка D, что AD = 10 и ∠BDC = ∠BAL = 60
◦
.
Найдите площадь треугольника ABC. Какова наименьшая площадь
треугольника BDC при данных условиях?
Задача 4. Найдите площадь фигуры, заданной на координатной
плоскости системой
(
|y + log
2
x| + |y + 1 − 2
x−1
| = |2y − 2
x−1
+ 1 + log
2
x|,
|x| + |y + 1| + |y − 1| = x + 2.
Задача 5. Точка O расположена в сечении AA
0
C
0
C прямоуголь-
ного параллелепипеда ABCDA
0
B
0
C
0
D
0
размером 2 × 6 × 9 так, что
∠OAB + ∠OAD + ∠OAA
0
= 180
◦
.
