Ковалюк Д.О., Москвіна С.М. Моделювання теплотехнологічних об’єктів з розподіленими параметрами
Подождите немного. Документ загружается.

130
14 6 10 5 6 4
33 2
( ) 5,81 10 4,85 10 1,51 10
1,80 10 1,10 13173,80
Et T T T
TT T
−−−
−
=− ⋅ + ⋅ − ⋅ +
+⋅ + +
(4.52)
Враховуючи вираз (4.52), кількість внесеної з наступної позиції
теплоти буде визначатися як
11
()
in i i
QVET
+
+
=
⋅ . (4.53)
Складові теплового балансу, що відносяться до винесення теп-
лової енергії, згідно з [116], це:
1.
Теплота, що виноситься димовими газами з даної позиції ви-
палювання:
..
(( ) ) ()
out i s s пг г i
QVPRXVET=++⋅, (4.54)
де
i
T
– температура димових газів на поточній позиції.
Враховуючи (4.52), вираз (4.54) перепишеться у вигляді:
1
()()
out i i i
QVVET
+
=
+⋅ (4.55)
2.
Теплота, що передається керамічним виробам від димових
газів [116]:
( )
z
gz
QSTT
α
=
⋅⋅ − , (4.56)
де
S – площа поверхні нагріву; ,
g
z
T Т – температура газового середо-
вища і матеріалу;
α
– коефіцієнт тепловіддачі.
Враховуючи формули (4.46)–(4.56), запишемо критерій оптимі-
зації у вигляді квадратичного відхилення між теплотою, що вноситься
і виноситься з системи,
()
2
11
11
(1 ) ( )
(,)
()()
р
ін is пов ii
iii gz
VQ VR X E V E T
FTV
VVET STT
α
++
+
⎛⎞
+
++ −
⎜⎟
=
⎜⎟
−+ −⋅−
⎝⎠
(4.57)
Оскільки функціонування теплотехнологічного ОРП полягає у
підтриманні певного температурного поля
T за допомогою парамет-
рів управління
U, то фізичний зміст цього критерію полягає у визна-
ченні таких значень об’єму газу, при яких втрати є мінімальними.
Основними труднощами при розв’язанні задачі оптимізації
(4.57) є невідомі значення температури матеріалу на всіх позиціях те-
плотехнологічного ОРП (крім першої), тому розглянемо формули для
розрахунку температури виробів в залежності від температури газово-

131
го середовища. Згідно з [116] за одиницю часу вироби отримують
приріст теплоти:
()
g
z
dQ
ST T
dt
α
=⋅⋅ − , (4.58)
що змінює температуру виробів на:
()
z
zzz
dT dQ
t
dt M c T
=
⋅Δ
⋅
, (4.59)
де
z
M
– маса виробів; (0,837 0,00064 )
z
z
cT=+ ⋅ – теплоємність садки;
tΔ – час перебування виробів на позиції печі.
Враховуючи складність та жорсткий регламент роботи ТОРП,
розглянемо функціональні обмеження, що накладаються на
розв’язання задачі визначення оптимальних параметрів.
Відповідно до методу визначення оптимальних параметрів мо-
делі теплотехнологічного ОРП першим етапом є визначення максима-
льно можливої марки виробів. Враховуючи специфіку ЛІ-моделі кла-
сифікації, на виході моделі отримуємо клас міцності виробів та зна-
чення градацій, при яких досягається цей клас міцності. Тобто, дана
модель в задачі оптимізації запишеться у вигляді нерівностей ви
ду:
axb≤≤, де a,
x
, b – вектори-стовпці (
x
– фактор ЛІ-моделі; a, b –
верхня і нижня границі градацій факторів):
1
...
n
x
x
x
= ;
1
...
n
a
a
a
=
;
1
...
n
b
b
b
=
. (4.60)
Таким чином, в результаті задачі класифікації якості продукції з
використанням ЛІ-моделі отримано лінійні обмеження на показники
сировини та підготовчих етапів, а також на температури печі.
Обмеження діапазону зміни управляючих параметрів задається
такими нерівностями:
min max
min max
;
;
,
iii
m
iii
VVV
Wconst
TTT
≤<
⎧
⎪
=
⎨
⎪
≤<
⎩
(4.61)
132
де
i
V – обмеження на пропускну здатність газових пальників;
m
W –
швидкість переміщення виробів;
i
T – технологічні обмеження на тем-
пературу в печі.
Беручи до уваги розроблені математичну модель прогнозування
якості продукції ТП виготовлення кераміки, математичну модель кла-
сифікації марки виробів, математичну модель коригування темпера-
турного поля та критерій ефективності, визначимо клас задачі оптимі-
зації (4.1), (4.2) і можливі методи її розв’язання.
Зауважимо, що розв’язання задачі оптимізації може бути засто-
соване у двох різн
их випадках: для визначення оптимального
темпе-
ратурного поля перед процесом випалювання та для коригування тем-
пературного поля безпосередньо в процесі випалювання. Основна ві-
дмінність між цими випадками зумовлена допустимою швидкістю
розв’язання задачі оптимізації. Так в першому випадку пропонується
використовувати нейромережеву модель якості продукції, оскільки
вона дозволяє отри
мати більш точний результат. В другому проп
ону-
ється використати модель коригування температурного поля.
Розглянемо задачу оптимізації (4.1), (4.2) з використанням мо-
делі коригування [98], тобто для випадку коригування температурного
поля. Оскільки модель коригування міцності виробів отримано в яв-
ному вигляді
pp
xbxbby
+
++
=
...
110
, то запишемо її як обмеження за-
дачі оптимізації
011
() ...
pp
gx b bx bx y=+ ++ −. (4.62)
Зауважимо, що значення
y задається до початку оптимізації як
нижня границя міцності для цього класу з певним запасом
Δ . Так, на-
приклад, для класу міцності ”М100”, нижня середня межа міцності
складає 100. Спираючись на точність (середнє відхилення) отриманих
регресійної і нейромережевої моделей вибираємо значення запасу мі-
цності 2
Δ= .
Враховуючи вищесказане, задача оптимізації (4.1), (4.2) запи-
шеться у вигляді:
() min
f
→T , (4.63)
133
min max
min max
() 0;
;
;
;
.
iii
m
iii
g
axb
VVV
Wconst
TTT
⎧
=
⎪
≤≤
⎪
⎪
≤<
⎨
⎪
=
⎪
⎪
≤<
⎩
T
(4.64)
Зазначимо, що критерій ефективності (4.63) є нелінійним відно-
сно температурного поля T, що пов’язано з нелінійною залежністю
()
E
T в формулах (4.53)–(4.55). Тому, задача оптимізації (4.63), (4.64)
є задачею пошуку мінімуму нелінійної цільової функції при заданих
лінійних обмеженнях, тобто задачею нелінійного програмування.
З теорії оптимізації відомо [3, 25, 41, 42, 138], що для цього да-
ного класу задач використовуються прямі та непрямі методи. Прямі
методи (метод проекцій градієнта, комплексний метод Бокса) оперу-
ють безпосередньо з вихідними задачами оптимізації і генерують пос-
лідовності точок {[
]}
x
k , таких, що ([ 1])
f
xk
+
([])
f
xk
<
, внаслідок чо-
го такі методи часто називають методами спуску. В цих методах ма-
тематичний перехід на деякому k -му кроці від точки []
x
k до точки
[1]
x
k + можна записати в такому вигляді
[1] [] p[k]
k
xk xk a
+
=+ , (4.65)
де []
p
k – вектор, який визначає напрямок спуску;
k
a
– довжина кроку
вздовж цього напрямку.
При цьому в одних алгоритмах прямих методів точки []
x
k ви-
бираються так, щоб для них виконувалися всі обмеження задачі, а в
інших ці обмеження можуть порушуватися на деяких або на всіх іте-
раціях. Таким чином, в прямих методах при виборі напрямку спуску,
обмеження враховуються в явному вигляді.
Непрямі методи (різні модифікації методу штрафних функцій)
зводять вихідну задачу нелінійного програмування до послідовності
задач безумовної оптимізації деяких допоміжних функцій. В цих ме-
тодах обмеження вихідної задачі враховуються в неявному вигляді.
Важ
ливо
ю особливістю застосування методів розв’язання задач
нелінійного програмування є те, що вони гарантують знаходження
глобального оптимуму лише в тому випадку, коли задача нелінійного

134
програмування зводиться до задачі випуклого програмування. В ін-
шому випадку для знаходження глобального оптимуму необхідно ви-
користовувати інші методи, такі як динамічне програмування [138]
або генетичні алгоритми [120].
Для можливості застосування методів оптимізації дослідимо ви-
пуклість вниз критерію ефективності, в цьому випадку знайдений оп-
тимум буде глобальним. Оскільки критерій ефективності є сумою од-
нотипних функцій, що описують мат
ематичну модель теплового бал
а-
нсу для окремої зони, то для дослідження випуклості всього критерію
достатньо дослідити на випуклість лише функцію (4.57).
Відомо, що функція ()
f
x називається випуклою вниз, якщо для
будь-яких
1
x
і
2
x
, і числа
α
, 0 1
α
≤
≤ виконується нерівність
121 2
( (1)) ()(1)()
f
x x fx fx
α
αα α
+− ≤ +− (4.66)
Відмітимо, що зазвичай провести аналіз, використовуючи лише
визначення випуклої функції, досить важко. Як показано в [25], для
цієї мети необхідно використовувати більш тонкі властивості випук-
лих функцій, визначені в такій теоремі [3]: для того, щоб функція
()
f
x , двічі диференційована на відкритій випуклій множині
M
, була
випуклою вниз необхідно і достатньо, щоб матриця Гессе була додат-
ньо визначеною.
Згідно з критерієм Сильвестра [3] в додатньо визначеній матриці
всі головні мінори матриці більші або дорівнюють 0. Враховуючи те,
що для двох сусідніх позицій ОРП, цільова функція містить 4 змінні
(позначимо їх умовно
112 2
,,,TVTV), можемо записати:
2
2
1
0
F
T
∂
≥
∂
, …,
2222
2
11 12 12
1
2222
2
11 12 1 2
1
2222
2
21 21 2 2
2
2222
2
21 21 22
2
0
FFFF
TV TT TV
T
FFFF
VT VT VV
V
FFFF
TT TV TV
T
FFFF
VT VV VT
V
∂∂∂∂
∂∂ ∂∂ ∂∂
∂
∂∂∂∂
∂∂ ∂∂ ∂∂
∂
≥
∂∂∂∂
∂∂ ∂∂ ∂∂
∂
∂∂∂∂
∂∂ ∂∂ ∂∂
∂
(4.67)

135
Оскільки змінні температури входять в цільову функцію зі сте-
пенем шість, то для визначення області випуклості цільової функції в
роботі запропоновано знайти області допустимих значень T , для кож-
ного з чотирьох рівнянь з подальшим виконанням операції перетину,
для визначення загальної області допустимих значень. В результаті
розрахунку визначників (4.67) отримано систему з чотирьох неліній-
них рівня
нь, множина розв’язків якої була отримана методом перебо
-
ру значень змінних
11
,, ,
iii i
TVT V
+
+
, всередині області їх допустимих
значень (технологічних обмежень). Результати дослідження області
випуклості функції (4.57), проведеного в пакеті Мatlab, показали, що
область допустимих значень змінних задачі оптимізації належить об-
ласті випуклості функції, а тому задача оптимізації буде мати єдиний
розв’язок.
Для розв’язання задачі оптимізації (4.63), (4.64) в роботі пропо-
нується використати метод послідовного квадратичного п
рограмуван-
ня SQP, який сьогодні
є одним з найсучасніших методів в області не-
лінійного програмування [25, 138], і дозволяє досить точно імітувати
метод Ньютона для задач умовної оптимізації. Реалізація методу
SQPскладається з трьох стадій: коригування матриці Гесе для функції
Лагранжа, розв’язання задачі квадратичного програмування, обчис-
лення лінійного пошуку і функції вигоди. Розв’язання задачі оптимі-
зації проводилося в мат
ематичному пакеті Matlab з використанням ін-
струментарію Optimization Toolbox.
4.3. Розв’язання задачі оптимізації параметрів моделі
Дослідження ефективності запропонованого методу визначення
оптимальних параметрів моделі теплотехнологічного ОРП було здійс-
нено на ВАТ “Керамік” (м. Вінниця).
Значення параметрів технологічного процесу виготовлення бу-
дівельної кераміки для моделювання температурного режиму взято з
довідників [132, 116], технологічного регламенту [133] та конструк-
торської документації ВАТ “Керамік” [112].
Оскільки в процесі промислової експлуатації тунельної печі
встановлені максимальні значення температурного поля:
136
max
[550, 700, 760, 800, 840, 880, 920, 940, 950,T = 900, 720, 640, 570],
то ефективність запропонованого методу полягає у знаходженні ново-
го вектора температурного поля, який дозволить отримати таку ж ма-
рку виробів, але з меншим використанням енергетичних ресурсів.
Дослідження методу визначення оптимальних параметрів моде-
лі теплотехнологічного ОРП були проведені для трьох різних груп ви-
робів: перша – з різними значеннями пластичності
23
A
lO, друга – з рі-
зними значеннями вмісту оксиду магнію
M
gO, третя – з різними зна-
ченнями вологості сирцю після сушіння _Wsyr. До кожної з груп бу-
ли відібрані 3 партії виробів (по два зразки), значення параметрів яких
крім досліджуваних показників є однаковими.
Дослідження кожної партії виробів були проведені за такою
схемою:
1)
фіксувалися значення параметрів ТП (наведені в табл. 4.9);
2)
прогнозувався максимально можливий клас міцності виробів
по ЛІ-моделі ризику при даних значеннях параметрів ТП та максима-
льних значеннях температурного поля
max
T
;
3)
в результаті розв’язання задачі оптимізації (4.1), (4.2), визна-
чалися нові значення температурного поля
opt
T – уточненні значення
параметрів нечіткої моделі теплотехнологічного ОРП;
4)
в процесі випалювання:
а) для першого зразка партії встановлювалися
max
T значення те-
мпературного поля, визначалась кількість витрачених енергетичних
ресурсів при його підтриманні та міцність виробів;
б) для другого зразка партії встановлювалися
opt
T значення тем-
пературного поля, визначалась кількість витрачених енергетичних ре-
сурсів при його підтриманні та міцність виробів;
5)
порівнювалися показники міцності виробів та кількість ви-
трачених енергетичних ресурсів двох зразків партії.
Результати проведених досліджень наведені в табл. 4.10.

137
Таблиця 4.9
Експериментальні значення параметрів ТП
№ партії Al2О3 MgО W_pov Tyaga Dry_T W_syr
Значення ТП для різних значень пластичності
A
l
1 7,60 8,70 80 3 48 7,8
2 8,00 8,65 80 3 48 7,8
3 8,51 8,72 80 3 48 7,9
Значення ТП для різних значень вмісту
M
gO
4 8,15 8,49 80 3 48 7,8
5 8,20 7,20 80 3 48 7,8
6 8,20 7,80 80 3 48 7,7
Значення ТП для різних значень вологості сирцю
7 8,22 7,82 75 3 48 7,2
8 8,24 7,85 75 3 48 7,8
9 8,20 7,80 75 3 48 8,4
Таблиця 4.10
Результати методу визначення оптимальних параметрів ОРП
№
Клас
міцн. при
max
T
Оптимальне температурне поле,
o
p
t
T
Міцн.
при
o
p
t
T
Енерг.
витрати,
3
ì
1 75
[517,638,702,773,834,862,931, 940,935,887, 663,587,514]
82,6 325/284
2 100
[531, 62 4,684,724,803,857, 908,918,914,864,645,612,563]
104,4 328/276
3 100
[542, 614,675,723,774,842, 866,900,890,880,760,635,540 ]
105,2 321/264
4 100
[525,647,706,771,798,864,928,940,940,883 ,676,587,524]
103,7 319/271
5 100
[510,696,796, 845,870,900,905,910,900 ,834,670,573,552]
115,2 321/268
6 100
[530,650,710,743,808,879,936, 940,924,862,667,602, 533 ]
109,7 311/289
7 100
[524,654,716,763,819,872,940,950,944,864,674,608,563]
118,3 332/301
8 100
[526,645,719,761,814,867,938,944,936, 868,654,610,536]
114,2 324/294
9 100
[551,712,765,783,815,852, 889,907, 908,851, 6 69,615,564]
108,4 318/281
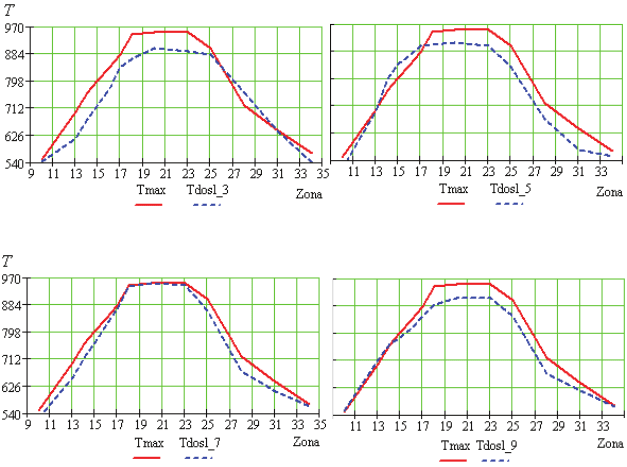
Результати методу визначення оптимальних параметрів в графі-
чному вигляді наведені на рис. 4.10, де
max
T – еталонна (максимальна)
крива; Tdosl – температурна крива для i -го досліду. Результати моде-
лювання, наведені в табл. 4.10 показали, що використання запропоно-
ваного в роботі методу визначення оптимальних параметрів теплотех-
нологічного ОРП дозволяє розрахувати такі параметри моделі тепло-
технологічного ОРП, при яких досягається максимальний клас міцно-
138
сті, проте з меншими енергетичними витратами. Зазначимо, що під
енергетичними витратами в роботі розуміється об’єм газу, що пода-
ється на пальники для підтримання цієї температури.
Рис. 4.10. Температурні криві випалювання
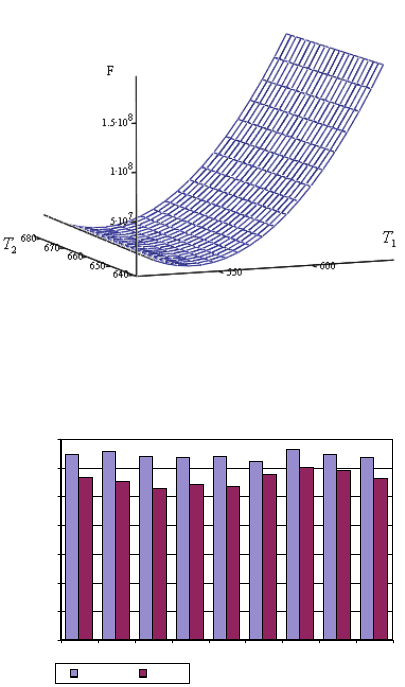
В результаті розв’язання задачі оптимізації (4.1), (4.2) дослідже-
но залежність цільової функції втрат (4.57) від значень температурно-
го поля. На рисунку 4.11 представлена отримана залежність енергети-
чних витрат від температур перших двох позицій ОРП, з якої можна
зробити висновок, що мінімальні енергетичні витрати досягаються у
випадку, коли різниця цих температур не перевищує 60
°С, що повніс-
тю узгоджується з технологічним регламентом.
Для кількісної оцін
ки об’єму всього зекономленого газу розгля-
немо колонку “енерг. витрати” (табл. 4.10). Перше число вказує об’єм
газу (по всій печі) при максимальній температурній кривій
max
T , друге
– при
opt
T .
139
Рис. 4.11. Дослідження цільової функції для першої та другої зон ОРП
Графічне представлення використаного об’єму газу при
max
T і
opt
T наведено на рис. 4.12.
0
50
100
150
200
250
300
350
123456789
експерименти
витрати палива
Тmax Topt
Рис. 4.12. Порівняння об’єму використаного газу при
max
T
і
opt
T
Використовуючи значення витраченого газу, розраховано, що
метод визначення оптимальних параметрів моделі теплотехнологічно-
го ОРП дозволяє в середньому для однієї партії (вагонетки) виробів
зекономити 7,14 % палива.
Таким чином, беручи до уваги наведені результати розв’язання
задачі оптимізації та проведених експериментальних досліджень, мо-
жна зробити висновок про ефективність запропонованого методу ви-
значення оптимальних параметрів теплотехнологічного ОРП.
