Kothari D.P., Nagrath I.J. Modern Power Systems Analysis
Подождите немного. Документ загружается.

E4
|
Modern
Power
SYstem
AnalYsis
conducting
horizontal
shdet
of infinite
extent
which
therefore
acts
like
an
equipotential
surface.
and
unit
is
such
that
it
has
a zero
potential
plane midway
between
the
conductors
as
shown
in Fig.
3.8.
If a
conducting
sheet
of
infinite
dimensions
is
placed
at the
zero
potential
plane,
the
electric
field
remains
undisturbed.
Further,
if the
conductor
carrying
charge
-q
is
now
removed,
the
electric
field
above
the
conducting
sheet
stays
intact,
while that
below
it
vanishes.
Using
these
well
known
results
in
reverse,
we
may
equivalently
replace
the
presence
of
ground
below
a charged
conductor
by
a fictitious
conductor
having
equal
and
opposite
charge
and
located
as
far below
the
surface
of
ground
as
the
overhead
conductor
above
it-such
a fictitious
conductor
is
the
mirror
image
of
the
overhead
conductor.
This
method
of
creating
the
same
electric
field
as in
the
presence
of
earth
is known
as the
method
of
images
originally
suggested
by
Lord
Kelvin.
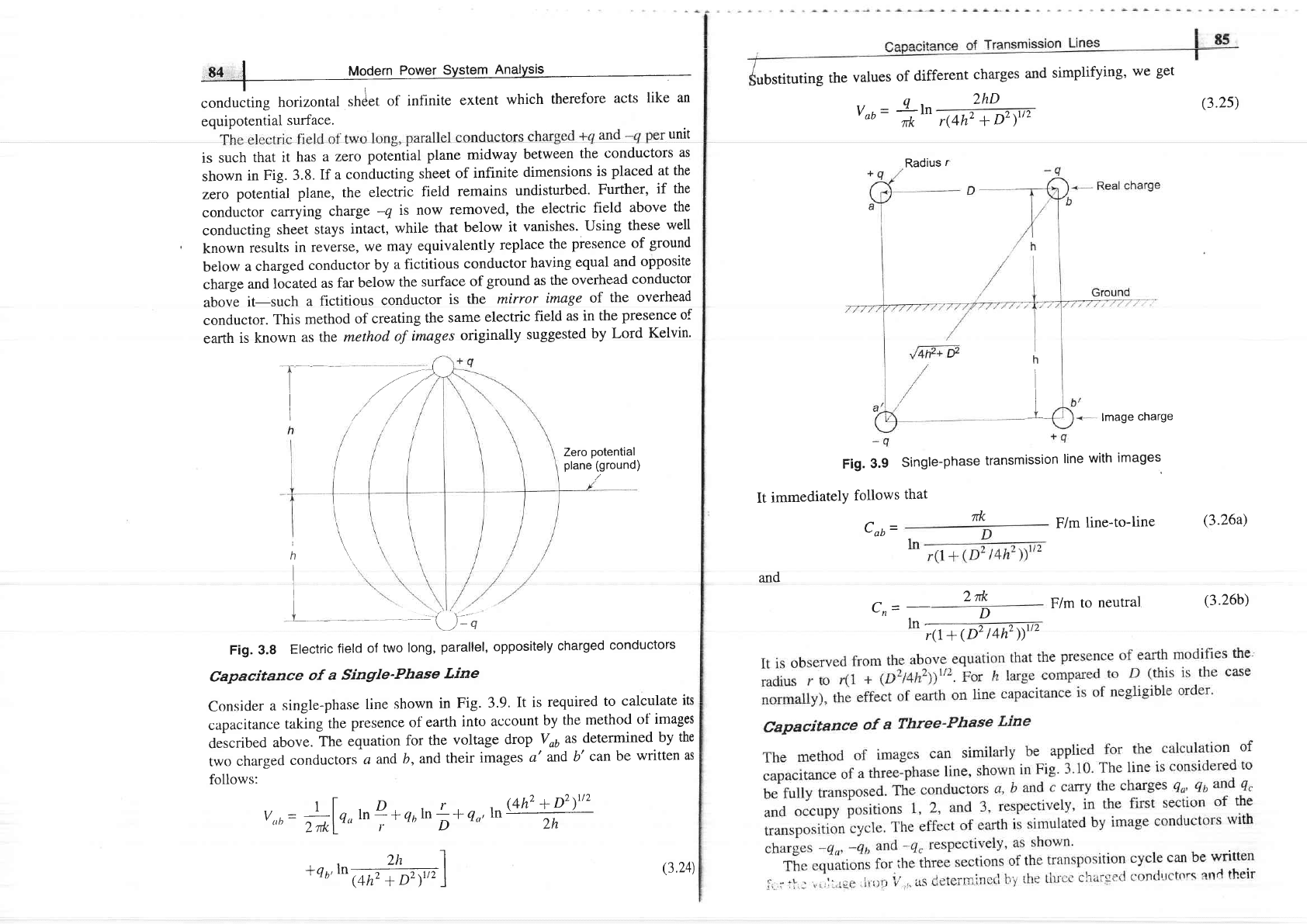
Zero
potential
plane (ground)
Fig. 3.8
Electric
field
of
two
long,
parallel, oppositely
charged
conductors
Capacitance
of
a
Single'Phase
Line
Consider
a
single-phase
line
shown
in
Fig.
3.9.lt
is
required
to
calculate
its
capacitance
taking
the
presence
of
earth
into
acoount
by
the
method
of
images
described
above.
The
equation
for
the
voltage
drop
Vo6
as
determined
by
the
two
charged
conductors
a
and,
b, and
their
images
a'and
b'
can
be
written
as
follows:
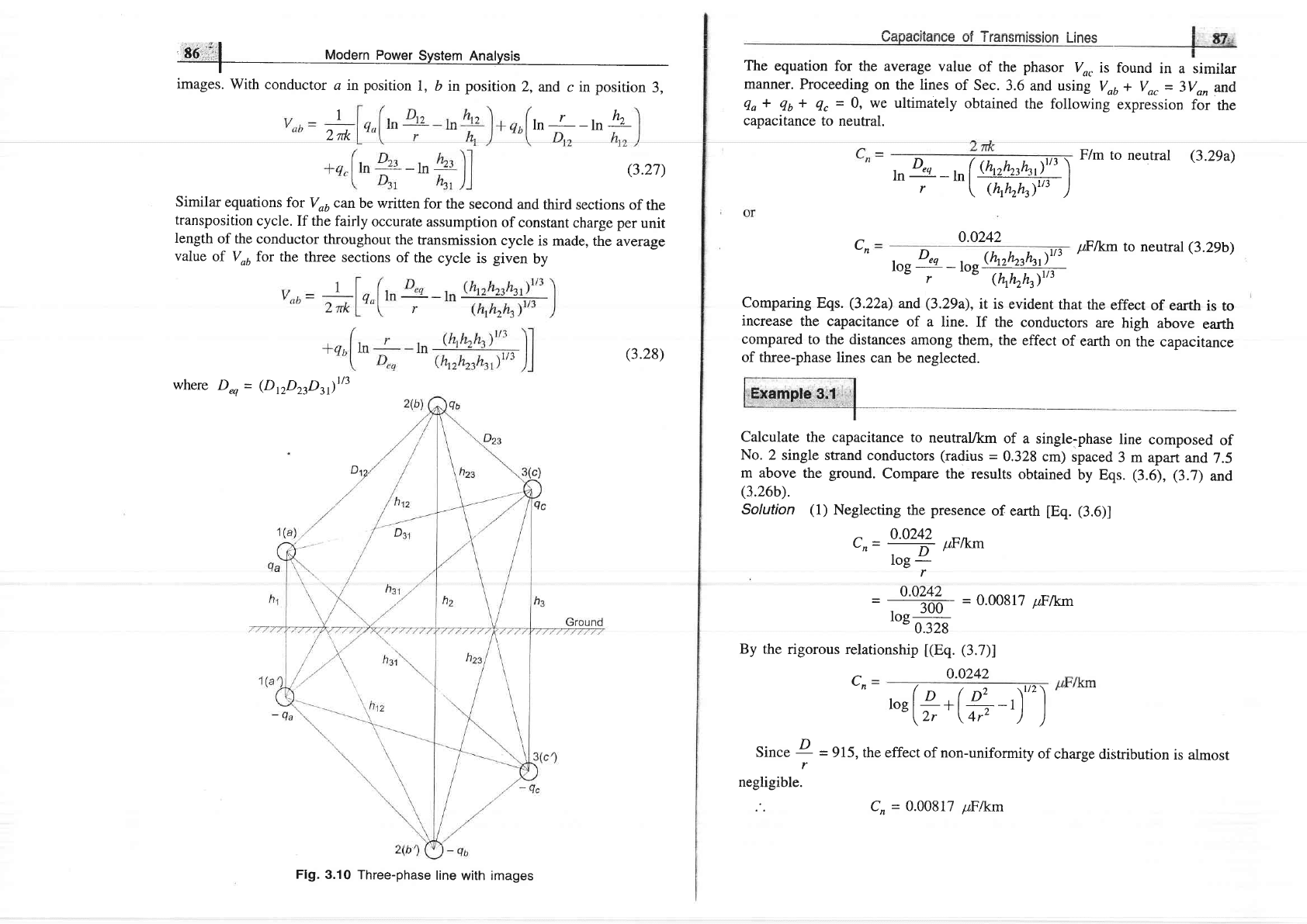
lmage
charge
Fig'3.9Sing|e-phasetransmissionIinewithimages
It
immediatelY
follows
that
wab
-
F/m
line-to-line
(3.26a)
2hD
Vob=
r(4hz +
D2)'tz
Radius
r
(3.2s)
F/m
to
neutral
(3.26b)
'l
rn
rk
l--
t,
h\,
I
t__
h
I
I
I
/'7
irk
and
Cn=
-
2nk
D
ln
v
ub
=
*1,
"
m
2
+
nrrn
i*
e,,,
t"gt#Y
*q,,tnGFfUl
41+tO't4h21stt2
ubstituting
the
values
of
different
charges
and
simplifying'
we
get
(3.24)
86
,*
|
Modern
power
Svstem
Analvsis
images.
with
conductor
a in position
1,
b in position2,
and
c in
position
3,
ln
r
-
ln
h,
(3.27)
Similar
equations
for
Vo6 can
be written
for
the second
and
third
sections
of
the
transposition
cycle.
If the
fairly
occurate
assumption
of
constant
charge per
unit
length
of the
conductor
throughout
the
transmission
cycle
is
made, the average
value
of Vou
for the
three
sections
of
the
cycle is
given
by
Capacitanee
of Transmission
Lines
The
equation
for the
average value
of the phasor
%.
ir found
in a similar
manner.
Proceeding
on the lines
of
Sec. 3.6
and using
Vou *
Vo,
=
3Von
and
Qo
*
Qt
*
Qc
=
0,
we
ultimately
obtained
the
following
expression
for
the
capacitance
to neutral.
F/m
to
neutral
(3.29a)
1
2 7rl(
tn
D'u
-
rr(
rn"n"\'),)!t
\
r
(
(hrlhhs)'''
)
0.0242
C,
pPttcm
to neutral
(3.29b)
lon
D'n
-
ron@"httu')'!t
--o
r
--o
(4h24)tt3
(3.28)
Comparing
Eqs.
(3.22a)
and
(3.29a),
it is evident
that
the
effect
of
earth
is
to
increase
the capacitance
of
a line.
If the
conductors
are high
above
earttr
compared
to the distances
among them,
the
effect
of
earth
on
the capacitance
of three-phase
lines
can be
neglected.
Calculate
the capacitance
to
neutrallkm
of
a single-phase
line
composed
of
No.
2 single
strand conductors
(radius
=
0.328
cm)
spaced
3 m apart
and,7.5
m
above
the
ground.
compare
the results
obtained
by
Eqs.
(3.6),
(3.7)
and
(3.26b).
Solution
(1)
Neglecting
the
presence
of
earth
tEq.
(3.6)l
^
0.0242
n,
C,=31fitkm
log
-
o.oi+z
=ffi=o'00817
P'Flkm
-
0.328
By the
rigorous relationship
[(Eq.
(3.7)]
cn
o.0242
where
D,
=
(DnDnDrr)"t
"'(+.(#-')"')
Since
+
=915,
the effect of non-uniformity
of
charge
distribution
is almost
negligible.
C"
=
0.00817 pFkm
Flg.
3.10
Three-phase
line
with images

c'-
o:o??
=
o'0082
P'Fkm
"
2.9s3
Note:
The
presence
of earth
increases
the
capacitance
by
approximately
3
parts
in
800.
rrl
_uu
I
Modern
powel€ysteryr_Anslygls
-
(2)
Considering
the eff'ect
of
earth and neglecting
non-uniformity
of
charge
distribution
[Eq.
(3.26b)]
0.0242
Capacitance of Transmission Lines
|
89
-----------l
bca
d=8m
-
-
h=6m
Fig.
3.11 Cross-section of a double-circuit
three-phase line
Solution
As
in Sec. 3.6,
assume that the
charge
per
conductor
on
each
phase
is equal in all
the
three sections of the
transposition cycle.
For section
/ of
the
transposition cycle
V,,n(l)
=
(3.30)
r(l*(
300
,Jto4
o32BJLo4
/4h"))
-
897
0.0242
tog(440/0.525)
Examp
le
3.2
A three-phase
50 Hz transmission
line
has flat
horizontal
spacing
with
3.5 m
between
adjacent
conductors.
The
conductors
are
No. 2/0
hard-drawn
seven
strand
copper
(outside
conductor
diameter
=
1.05
cm). The
voltage
of
the line
is 110
kV.
Find the
capacitance
to neutral
and
the charging
current
per
kilometre
of line.
Solution
D"o=
(3.5
x
3.5
x
'7)t't
=
4.4
m
vl_106
n"
-
u,Cn
-
314. o.oos%
=
0.384
x
106
O/km to neutral
charging
cunent
-
+-
(l
19l
]e)
x
l-000
Xn
0.384x 106
=
0.1I Aftm
For section
II of the transposition cycle
v"b
Gr)
=
,lAln.("i*
r"
#)+
c,
(rn;
.'"
*)
+a,(rnj.,":)]
(33r)
For section III
of
the transposition cycle
vtu
(rrr)
=
*lr.
('"
j
.^
i)+
a,
(rn
I.
^I)
+a.(rn;.r"f)f
,"r,
Average value
of Vo6
over the transposition
cycle is
given
by
v,*
(av
s)
=
iL*[n.'n
(ttrj+*
r,
^(###)]
z*l*(" i*'';)+c,(rn;
.'"f
)
*n.(,n
j+r";)]
The
six conductors
of a
double-circuit
three-phase
line having
an overall
radius
of 0.865 x
10-2
m are
arranged
as shown
in Fig.
3.11. Find
the capacitive
reactance
to neutral
and charging
current
per
kilometre per
conductor
at
110
kV,
50 Hz.

90
|
Modern
power
System
Analysis
i'B'
jh
,'f
'd
Capacitance
to
neutral
per
conductor
=
2dc
vou*
vo,=
3von=
fien"-
Qt-
q,)tn
(ffi)'''
(3.3s)
3von=*r"(:#)
Capacitance
of
Transmission
Lines
I
gf
-
l'.
h=6m
Fig.
3.12
3.8 METHOD
OF
GMD
(MODTFTED)
A comparison
of various
expressions
for
inductance
and
capacitance
of
transmission
lines
[e.g.
Eqs.
(2.22b)
and
(3.6)]
brings
our rhe
facr
that
the rwo
are sirnilar
except that
in
inductance
expressions
we
have
to
use
the
tictitious
conductor
radius
rt
=
0.7788r,
while
in
the
expressions
for
capacitance
actual
conductor
radius
r
is used.
This
fact
suggests
that
the
method
of
GDM
would
be applicable
in
the calculations
for
capacitance
as
well provided
it is
modified
by
using
the
outer conductor
radius
for finding
D,,
the
self geometric
mean
distance.
Exarnple
3.3 can
be conveniently
solved
as under
by using
the
rnodifled
GMD method.
For the
first
section
of the
transposition
cycle
mutual
GMD
is
Dub=
((ts)
(ts))tta
_
liglttz
Db'
=
Qil'''
Drr,
=
(
jh)'''
D
"n
(D"pop,o)r,t =
[(i,
grjh)r,t)t,,
ln
the first
section
of the
transposition
cycle
self
GMD
is
D,o
=
?f
rf
)rt4
=
?f)'''
D'l'
=
QAt''
Dr,
=
(At''
D,
=
(D,oDroD,,)''3
=
l?3f
Arl3fitz
2d(
2nk
=fi,^-,,)h(ffi)"'
(3.33)
(3.36)
(3.37)
Now
h=
6 m;
d
=
8
m;
-/
=
8
m.
Referring
to Fig.
3.I2,
we
can write
f ,
..?
.
, ,,121'1/2
r=lf/)-+(o-h\"1
:Jim
L\2)
\
2 ))
f
=
(j'+
h2)rt2
=
l0
m
g
=
(72
+
42)rt2
=J65
-
Conductor
radius
(overall)
=
0.865 x
10-2
m
Substituting
the values
for
various
distances.
we
have
4 rx7
x
8.85 x
10-12 x
106 x
1000
pF
/km
Total
capacitance
to
neutral
for
two
conductors
in
parallel
Cn=
4rk
1nf
rz*os*stof
roo
)3-l'/3
[
100x8
\0.86s/
|
=
0.018
I
1F/km
QC,=
314 x
0'0181
x
10-6
=
5.68
x
10-6
Ulkm
Charging
current/phase
=
"t#*
x
5.6g x
10{
=
0.361
Charging
current/conductor
=
0'361
L
cn
4 ltk
=
0.1805
A/km
Now
Cn=
F/m

ai
,'lt
I
F
This
result
obviously
checks
with
the
fundamentally
derived
expression
in
Example
3.3.
3.9
BUNDTED
CONDUCTORS
LsL
PROB
IE
M S
:::f ::i::t"^tll:;
j;;:i;g;:;fi
IH#,",iHffi
T,.$l;:i,h*j
A
bundled
conductor
line
is
shown
in
Fig.
3.13.
The
conductors
of
any
one
bundle
are
in
parallel,
and
it
is
assumed
that
the
charge
per
bundle
divides
equally
among
the
conductors
of
the
bundle
as
Drr>
r/.
Also
Drr-
d
x
D*
+
d
x
D12for
the
same
reason.
The
results
obtained-with
these
urru'rnptions
are
fairly
accurate
for
usual
spacings.
Thus
if
the
charge
on phase
a
is
qo,
the
conductors
a
and
a'have
a
charge
of qolz
each;
similarly
the
charge
is
equally
divided
for phases
b
and
c.
[?1
F-q--i
Fd+
aQ
I
O,,
oQ
I
eu,
"6
iec/____
_
DP
---->f-
Dzs
---------
l'
Dy
--
'..l
Fig'
3'13
Cross-section
of
a
bundled
conductor
three-phase
transmission
line
Now,
writing
an
equ'ation
for
the
voltage
from
conductor
a
to
condu
ctor
b,
we
get
vob=
*lotn,(rn4.*ro
-,
*o.Sq"lr"
o-u*
rn
4.
)
--\
D,
Dt,)
or
/
r
t
+.qntng.n"tnDrr\
v,,h
=
,*lr,
,n'.r
ro
,.,
Dtz
Dzt
)
applied
voltage
is
baranced
three-phase,
50
Hz.
Take
the
voltage
of
phase
a
as
reference
phasor.
All
conductors
have
the
same
radii.
Also
find
the
charging
current
of phase
a.
Neglect
the
effect
of grouno.
Fig.
p-3.1
3'2
A
three-phase
double-circuit
line
is
shown
in
Fig.
p-3.2.The
diameter
of
each
conductor
is
2.0
cm.
The
line
is
transffio
and
carries
balanced
load'
Find
the
capacitance
per
phase
to
neutral
of
the
line.
Qc'
Qu,
aQ
oQ
T
2m
,f
I
I
2m
_t
Considering
the
line
to
be
transposed
and proceeding
in
the
usual
manner,
the
final
result
will
be
',=
^ffi
p,Fkmto
neutral
where
Do,
=
(DnDnD3)In
It
is
obvious
from
Eq.
e.aD
that
the
method
of
modified
GMD
is
equally
valid
in
this
case (as
it
should
be).
3'3
A three-phase,
50
Hz
overhead
line
has
regularly
transposed
conductors
equilaterally
spaced
4
m
apart
The
"upu.Itun.e
of
such
a
line
is
0.01
tFkm'Recalculate
the
capacitanc.
p"i
kilometre
to
neutral
when
the
conductors
are
in
the
same
horizontai
prane
with
successive
spacing
of
4
m
and
are
regularly
transposed.
3'4
consider
the,
500
kv,
three-phase
bundled
conductor
line
as
shown
in
Fig'
P-2'9'
Find
the
capacitivi
reactance
to
neutral
in
ohms/km
at
50
Hz.
3.5
A
three-phase
trernsnri.ssion
rinc
has
r,rat,
horizontar
spacing
with
2
rn
between
adjacent
conductors.
The
radius
of
each
conductor
is
0.25
cm.
At
a
certain
instant
the
charges
on
the
centre
conductor
and
on
one
of
the
outside
conductors
are
identical
and
voltage
drop
between
these
identi-
cally
charged
conductors
is
775
v.xegtecithe
effect
of
ground,
and
find
the
value
of the
identical
charge
in
coulomblkm
at
the
instant
specified.
3'6
Find
the
50
Hz
susceptance
to
neutral
per
kilometre
of
a
double-circuit
three
phase
line
with
transposition
as
shown
in
Fig.
p_3.6.
Given
D
=
Jm
and
radius
of
each
of
the
six
conductors
is
1.3g
cm.
(3.3e)
(3.40)

94
i
-
Modern
Po*",
Syrt"r
An"lysi.
t
666565
l'-
o
-
+--
o-*_
D
>)<--
D
'l--
o-J
3.8
. P-3.6
Double
circuit three-phase
line with
flat
spacing
3.7
.{ single
conductor power
cable
has
a conductor
of No. 2 solid
copper
(radius
=
0.328 cm).
Paper insulation
separating
the
conductor
from
the
concentric
lead
sheath has
a thickness
of 2.5
mm and
a relative
permittivity
of 3.8.
The thickness
of the
lead sheath
is 2 mm.
Find
the
capacitive
reactance per
kilometre
between
the inner
conductor
and
the
lead
sheath.
Find
the capacitance
of
phase
to
neutral
per
kilometre
of a three-phase
line having
conductors
of 2 cm
diameter placed
at the corners
of a triangle
with sides
5
m,
6 m and
7 m respectively.
Assume
that the
line is
fully
transposed
and
carries
balanced
load.
Derive an
expression
for the capacitance
per
metre
length
between
two
long
parallel
conductors,
each
of radius,r,
with axes
separated
by a
distance D,
where
D
,,
r, the
insulating
medium
being air.
Calculate the
maximum potential
difference
permissible
between
the conductors,
if
the
electric
lield
strength between
them
is
not to exceed
25 kY
lcm, r being
0.3 cm and
D
=
35 cm.
REFERE
N CES
Books
l.
Stevenson,
w.D., Elements
of Power
System Analysis,4th
edn,
McGraw-Hill,
New
York,
1982.
Cotton, H.,
and
H. Barber,
The Transmission
and Distribution
of Electrical
Energy,3rd
cdn,
Hodder and
Stoughton,
1970.
Starr, A.T.,
Generation,
Transmission
and
Utilization of Electric
Power,
Pitman,
1962.
Papers
Parton,
J.E. and
A. Wright,
"Electric
Stresses
Associated with
Bundle
Conduc-
tors", International
Journal
of ELectrical Engineering
Education
1965,3 :357.
Stevens, R.A. and
D.M.
German,
"The
Capacitance
and Inductance
of
Overhead
Transmission
Lines", International
Journal
of Electrical
Engineering
Education,
1965,2 :71.
4.I INTRODUCTION
A complete diagram of a
power
system representing
all the
three
phases
becomes too complicated for
a system of
practical
size,
so much so
that it
may
no longer
convey the information it is
intended to
convey. It
is much
more
practical
to represent a
power
system
by means of simple
symbbls
for
each
component
resulting in what is called
a one-line diagram.
Per unit system leads to
great
simplification
of three-phase
networks
involving transformers.
An impedance
diagram drawn
on a
per
unit
basis does
not require ideal transfbrrners to be
included in it.
An important element of a
power
system is the
synchronous
machine, which
greatly
influences the system behaviour
during
both steady
state and
transient
conditions. The
synchronous machine model
in steady
state is
presented
in
this
chapter. The transient model of the
machine will
be
presented
in
Chapter
9.
4.2 Single-Phase
Solution of Balanced Three-Phase
Networks
The solution of a three-phase network under
balanced
conditions
is
easily
carried out by solving the single-phase network corresponding
to
the ref'erence
phase.
Figure 4.1
shows
a
simple, balanced three-phase
network.
The
generator
and load neutrals are therefore at the same
potential,
so that In
=
0. Thus
the
neutral impedance Zn does not affect network
behaviour.
For
the reference
phase
a
En=
(Zc+
ZL)I'
3.9
2.
3.
A
T.
5.
(4.1)
The currents and
voltages
in the other
phases
have
the same
magnitude
but
are
progressively
shifted
in
phase
by
120".
Equation
(4.1)
conesponds
to
the
single-phase network of Fig.
4.2
whose solution completely
determines
the
solution
of the three-phase network.

Modern
power
System
Alelygis
Ia
\;
\e,
*c)
t
L_-l
-
.*-
'-
zn
In=o
trb
16
Z1
Ic
Representation
of Pgryer
System
Components
If the transformer
is
YIA connected
as
in-Fig.
4.4a,
the delta
side
has to
be
replaced
by an
equivalent
star connection
as shown
dotted
so
as
to obtain the
single-phase
equivalent of
Fig. 4.4b.
An important
fact has,
however,
to
be
AN
m0 lrne
culTent
/A
have
a
certain
phase
angle
shift- from
the
star
side values
Vorand
Io(90" for
the
phase
labelling
shown).
In the
single-phase
equivalent (Vew,
I)
are
respectively
in
phase
with
(Von,
/o). Since
both
phase
voltage
and
line current
shift through
the same
phase
angle
from
star
to delta
side, the
transformer
per
phase
impedance
and
power
flow are
preserved
in the
single-phase
equivalent.
In most
analytical
studies, we
are merely
interested
in the
magnitude
of
voltages
and currents
so that
the
single-phase
equivalent
of Fig. 4.4b
is an
acceptable
proposition.
Wherever
proper
phase
angles
of currents
and voltages
are needed,
correction
can
be easily applier
after
obtaining
the solution
through
a single-
phase
transformer equivalent.
(a)
Y/A
transformer
with
equivalent
star connection
-l
,",
lrJ'ZL
!:
Fig.
4.1
Balanced
three-phase
network
Ea
Fig'
4.2
Single-phase
equivalent
of
a
balanced
three-phase
network
of Fig.
4.1
Z6
€l>
Ia
->,
A
Ia
(a)
Three-phase
Y/y
transformer
(b)
Single-phase
equivalent
of
3-phase
y/y
transformer
n_
(b)
Single-phase
equivalent
of Y/A
transformer
Fig.4.4
It may be noted here
that irrespective
of the
type of
connection,
the
transformation
ratio
of the single-phase
equivalent
of
a three-phase
transformer
is the
same as the line-to-line
transformation
ratio.
'
See
Section 10.3.
Fig.
4.3

Yr
i
v--
q
r
,
Fig.
4.5
One-line
representation
of a
simple
power
system
Generator
No.
1 :
30 MVA,
10.S
kV,
X'
=
1.6
ohms
1
Generator
No. 2
: 15
MVA,
6.6 kV, X'
=
1.2
ohms
Generator
No.
3: 25 MVA,
6.6 kV,
X'=
0.56
ohms
Transformer
11
(3
phase)
: 15
MVA,
33/1 1
kV,
X
=
15.2
ohms
per phase
on high
tension
side
Transformer
Tr(3
phase):
15
MVA,
3316.2
kV,
X=
16
ohms
per
phase
on frign
tension
side
Transmission
line:
20.5
ohms/phase
Load
A : 15 MW,
1 1
kV,
0.9
lagging
power
factor
Load
B:
40 MW,
6.6 kV,
0.85lagging
power
factor
Note:
Generators
are
specified
in
three-phase
MVA,
line-to-line
voltage
and
per
phase
reactance (equivalent
star).
Transformers
are
specified
in three-phase
MVA,
line-to-line
transformation
ratio,
and
per
phase
(equivalent
star) impedance
on
one
side.
Loads
are
specified
in three-phase
MW, line-to-line
voltage
and
power
factor.
I-
r_-1
--i--t
I--ntrn^'"1'"rr'
f-
I
'-litr-d-'r,n'rq
J-'rn,A,n-?fi-d\
1 r- i , I
tro I
Yli
i
Modern
Power
System
Analysis
I
4.3
ONE.IINE
DIAGRAM
AND
IMPEDANCE
OR
REACTANCE
DIAGRAM
A
one-line
diagram
of
a
power
system
shows
the
main
connections
and
showrr
depending
on the
information
required
in
a
system
study,
e.g.
circuit
breakers
need not
be
shown
in
a load
flow
study
but
are
a
must
for a
piotection
study.
Power
system
networks
are
represented
by
one-line
diagrams
using
suitable
symbols
fbr
generators,
motors,
transformers
and loads.
It
is
a
convenient
practical
way
of
network
representation
rather
than
drawing
the
actual
three-phase
diagram
which
may
indeed
be
quite
cumbersome
and
confusing
for a practical
size
power
network.
Generator
and
transformer
connections-star,
delta,
and
neutral
grounding
are indicated
by symbols
drawn
by
the
side
of
the
representation
of
these
elements.
Circuit
breakers
are
represented
as rectangular
blocks.
Figure
4.5
shows
the
one-line
diagram
of a
simple
power
system.
The
reactance
data
of the
elements
are given
below
the
diagram.
T2
.tF
ft
-fl
lF
tl
at'
__'l
r-YA
rl
-
>Fr-F.
+ ::
--,F_..-:
-J;-ffi
Genl'
I
Transformerll
'
Line
'r'TransformerT2
--tC;/C"'S
Load
A
Load
g
Representation
of
Power
System
Components
t
99
The
impedance
diagram
on
single-phase
basis
for use
under
balanced
operating
conditions
can
be easily
drawn
from
the
one-line
diagram.
For
the
system
of
Fie.
4.5
the
impedance
diagram
is
drarvn
in
Frg.
4.6. Single-phase
transtbrmer
equivalents
are
shown
as
ideal
transformers
with transformer
impedances
have
been
neglected.
This
is a
fairly
good approximation
for
most
power system
studies.
The
generators
are
represented
as
voltage sources
with series
resistance
and
inductive
reactance
(synchronous machine
model
will be
discussed
in
Sec.
4.6).
The
transmission
line
is
represented
by
a
zi-model
(to
be
discussed
in
Chapter
5).
Loads
are
assumed
to be
passive
(not
involving
rotating
machines)
and
are
represented
by
resistance
and
inductive
reactance
in
series.
Neutral
grounding
impedances
do
not
appear
in
the
diagram
as
balanced
conditions
are
assumed.
Three
voltage
levels
(6.6.
I 1
ancl 33
kV)
are
present
in
this system.
The
throughout
this
book.
4.4
PER
UNIT
(PU)
SYSTEM
\
It
is
usual
to
express
voltage,
current,
voltamperes
and
impedance
of an
electrical
circuit
in
per
unit
(or
percentage)
of
base or
ret'erence
values
of these
quantities.
The
per
unit*
value
of
any
quantity
is defined
as:
the
actual
value
in
anY
units
the
base
or
reference
value
in the
same
units
The
per
unit
method
is
particularly
convenient
in
power systems
as the
various
sections
of
a
power
system
are
connected
through
translormers
and
have
different
voltage
levels.
Consider
first
a single-phase
system.
Let
Base
voltamPerss
=
(VA)s VA
Base
voltage
=
Vu
V
Then
(4.2a)
*Per
cent
value
=
per
unit
value
Per
cent
value is
not
convenient
computations.
T1
I
(
('
l
L
Yo
A-
Base
current
/u
=
-[4)e
\/
vB
A
x
100.
for
use
Fig.
4.6
lmpectance
diagram
of the
power
system
of Fig.
4.5
as the
factor
of
100 has
to be carried
in

tir.n' l
.,rvq..il
Mooern
Hower
system
Analysis
I
I
(4.e)
(4.2b)
Z(ohms)
x
(kVA),
Base
impedance
z,
=
Y-4-:
Vi
ohms
"
I
B
(VA)"
If
the
actual
impedance
is
Z
(ohms),
its per
unit
value
is
given
by
Z
(oltrns) x
(MVA)'
'er
unit
imPedance
Z
(Pu)
=
@
,r trt2 -, i n^n
z(pu)
=
J---
Z(ohms)
x
(vA)'
ZB
V;
For
a
power
system,
practical
choice
of
base
values
are:
Base
megavoltamperes =
(MVA)B
or
Base
kilovoltamperes
=
(kVA)B
Base
kilovolrs
=
(kv)a
Base
current
1,
1,000
x
(MVA)u
(kV)a
when
MVA
base
is
changecl
trom
(MVA)r,
oto
to
(MVA)a'
n'*'
andtV
base
s
changed
from
(kv)r,
oro
tJ
(kV)n,
new'
the
nt*
p"t
unit
impedance
from
Eq'
.4.9)
is
given
bY
Z(pu)n"*
=z(pu)o.,.
ffi"ffi
ohms
(4.3)
(4.4)
(4.s)
(4.6)
(4.7)
(4.10)
(4.11a)
Base
impedance
z-
-
1'ooq]
GV)r
,u
_
__Ia
_
GV)3
_
1,000
x
(kv)1
(MVA)B
(kvA)8
Per
Unit
Representation
of
a
Transformer
It
has
been
said
in
Section
4.2
that
a three-phase
transformer
forming
part
of
a
three-phase
system
can
be
represented
ty
a
single-phase
transformer
in
obtaining
per
phase
solution
of
the
system'
The
deltaconnected
winding
of
the
transformer
is
replaced
by
an
"quiuaient
star
so
that
the
transformation
ratio
of
the
equivalent
single-phase
transformer
is
always
the
line-to-line
voltage
ratio
of
the
three-Phase
transformer'
Figure4.Tarcpresentsasingle-phasetransfgrmlrintermsofprimaryand
secondary
leakagi
reactances
Zp
artd
Z,
and
an
ideal
transformer
of
ratio
1
:
a'
The
magnetizing
impedance
is
neglected.
Let
us
choose-a
voltampere
base
of
(vA)a
and
voltage
bases
on
the
two
sides
of
the
transformer
in
the
ratio
of
transformation,
i.e.
Vrs
-!
Vt,
a
(a)
Representation
of
single-phase
transformer
'-'
(mignetizing
impedance
neglected)
(b) Per
unit
equivalent
circuit
of
single-phase
transformer
Fig.
4.7
Z(ohms)
x
(kVA)u
(kV)?
x
1,000
In
a
three-phase
system
rather
than
obtaining
the per
unit
values
using
per
phase
base
quantities,
the per
unit
values
can
be
obtained
directly
Uy
u.ing
three-
phase
base
quantities.
Let
Three-phase
base
megavoltamperes =
(MVA,)B
Line-to-line
base
kilovolts
=
(kV)B
Assuming
star
connection
(equivalent
star
can
always
be
found),
Per
unit
impedance
z
(pu)
-
Z
(ohms)
x
(MVA),
(kv)"
Base
current
Ir-
l'ooox(MVA)u
o
Jr
1rv;u
Base
impedance
7o
-
l'ooox(kv)u
"
J3rB
_
GD3
_
1,ooo
x
(kv)2,
^L_-
(MVA)'
G"Ab
:
onms
-{_J--->
zs
12
(4.8)

-W I
todern
Power Srrstem -A-nalr-rsie
Y-
vr
v.vr.;
, rr rqt ystr
I
Therefore
=
a
(as
(VA)a
is
common)
I
'28
Representation
of
Power System
Uomponents
[,.t'ff.
l-
zz(pu)=
+-++o'1'
'
zzu
zB
zru
(4.1
i b)
(4.11c)
From
Fig.
4.7a
we
can
write
Vz=(Vt-Iflp)a-lrZ,
(4.12)
We
shall
convert
Eq.
(4.12)
into per
unit
form
Vz(pu)
Vzn
=
[Vr(pu)
V
w
-
I
r(pu)I
6Zo(pu)Zru]a
-Ir(pu)IruZ,(pu)Z*
Dividing
by
vzn
throughout
and
using
base
relations (4.
rra,
b, c),
we get
Vz(pu)
=
Vr(pu)
-
I,(pu)Zr(pu)
_
Ir(pu)Z,(pu)
(4.13)
Now
+=+=,
Ir
12
or
I'o
I'u
Ir(pu)=12(pu)=
1(pu)
Equation
(4.13)
can
therefore
be
written
as
Vz@u)
=
Vr(pu)-
(pu)Z(pu)
Z(pu)=Z,,(pu)+
Z,(pu)
Equation
(4.I4)
can
be
represented
by
the
simple
equivalent
circuit
of Fig.
4'7b
which
does
not
require
an
ideal
transfurmet.
Coniia.rable
simplification
has
therefore
been
achieved
by
the per
unit
method
with
a
common
voltampere
base
and
voltage
bases
on
the
two
sides
in
the
ratio
of transformation.
Z(pu)
can
be
determined
directly
from
the
equivalent
impedance
on primary
or
secondary
side
of
a transformer
by
using
the
appropriaie
impedancl
base.
On primary
side:
Zr=Zp+
Z,/a2
Z(pu)
=
+:!-+L*I
'
zru
Zro
z,o"a2
But
a2Ztn
=
Zzr
Zr(pu)
=
Zo(pu)
+
Z,(pu)
-
Z(pu)
On
secondary
side:
zz=
Z,
+
o2zo
Vrn
z
Vza
.
LaD
-
--
1,,
1,,
where
(4.r4)
Thus
the
per
unit
impedance
of a transformer
is the same
whether computed
from
primary
or
secondary
side so
long as
the
voltage
bases on the
two
sides
are in
the ratio
of transformation
(equivalent
per
phase
ratio of
a three-phase
transformer
which is
the same
as the ratio
of line-to-line
voltage rating).
The
pu
transformer
impedance
of
a three-phase
transformer is conveniently
obtained
by
direct use
of three-phase
MVA base
and line-to-line
kV base in
relation
(4.9).
Any other
impedance
on either
side of a transformer
is converted
to
pu value
just
like
Zo or
Zr.
Per Unit
Impedance
Diagram of a
Power System
From
a one-line
diagram
of
a
power
system
we
can directly
draw the impedance
diagram
by
following
the
steps
given
below:
1.
Choose
an
appropriate
common
MVA
(or
kVA) base for the system.
2. Consider
the system
to be
divided
into a number of sections by the
transfbrmers.
Choose
an
appropriate
kV base in one of the
sections.
Calculate
kV bases
of other
sections
in the ratio of transformation.
3.
Calculate
per
unit
values of
voltages and impedances in eqch
section
and
connect
them up
as
per
the topology
of the one-line diagram.
The
result
is the single-phase
per
unit
impedance diagram.
The
above
steps are
illustrated
by the fallowing
examples.
j
Example
4 1
Obtain
the
per
unit impedance
(reactance)
diagram of the
power
system of Fig.
4.5.
Solution
The
per phase
impedance
diagram of
the
power
system of
Fig. 4.5
has been
drawn in
Fig.
4.6. We shall make some further simplifying
assumptions.
1.
Line
capacitance
and resistance
are neglected
so that
it is
represented
as
a series
reactance
only.
2.
We
shall assume
that
the impedance
diagram is meant for short
circuit
studies.
Current
drawn
by static
loads under short circuit conditions can
be
neglected.
Loads
A and B
are therefore ignored.
Let
us
convert all
reactances
to
per unit form. Choose a common
three-phase
MVA
base
of 30
and a
voltage base
of 33 kV line-to-line on
the transmission
line.
Then
the
voltage base in the
circuit
of
generator
1 is 11 kV line-to-line and
that
in
the
circuits of
generators
2 and 3
is 6.2 kV.
The
per unit reactances
of
various components are calculated below:
(4.1s)
