Коршак А.А., Коробков Г.Е., Муфтахов Е.М. Нефтебазы и АЗС

Подождите немного. Документ загружается.

151

Таблица 4.6 — Эквивалентная шероховатость k

стальных труб

Вид труб Состояние труб

, мм

Диапазон

изменения

Среднее

значение

Бесшовные Новые и чистые 0,01…0,02 0,014

Сварные Новые и чистые 0,03…0,12 0,05

С незначительной кор-

розией после очистки 0,1…0,2 0,15

После нескольких лет

эксплуатации 0,15…0,3 0,2

Умеренно

заржавленные 0,3…0,7 0,5

Старые заржавленные 0,8…1,5 1

Сильно заржавленные

или с большими

отложениями 2…4 3

Для расчета λ в зоне смешанного трения турбулентного режима

(Re

< Re ≤ Re

) наиболее часто используется формула Альтшуля

0,25

0, 11

§·



¨¸

©¹

В зоне квадратичного трения турбулентного режима (Re > Re

)

расчет λ обычно ведут по формуле Шифринсона

λ = 0,11 · ε

0,25

Переходные числа Рейнольдса Re

и Re

для трубопроводов неф-

тебаз рекомендуется вычислять по формулам:

Re Re

III

10 500

;

. (4.4)

Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона

могут быть представлены зависимостью одного вида

(4.5)

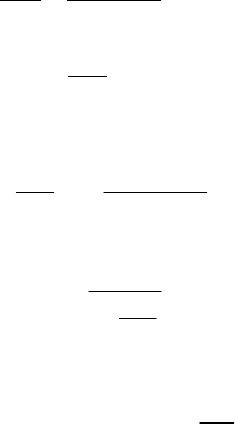
152

где А, m — коэффициенты, величина которых для каждой зоны тре-

ния неизменна.

Однако формула Альтшуля к виду (4.5) не приводится. Это ис-

ключает возможность решения гидравлических задач в общем

виде.

Около 30 лет назад В. Д. Белоусовым на основании анализа гра-

фика зависимости lg λ = ƒ(lg Re) были найдены приближенные зна-

чения коэффициентов А и m для зоны смешанного трения турбу-

лентного режима

A = 10

0,127 · lg ε – 0,627

, m = 0,123. (4.6)

Ту же задачу можно было решить следующим образом. При Re =

= Re

еще справедлива формула Блазиуса, а при Re = Re

уже мож-

но пользоваться формулой Шифринсона. Соответственно, с учетом

(4.4) для зоны смешанного трения получаем



0,25

0, 3164

0, 178

10 /



. (4.7)

0,25

0, 11 

. (4.8)

Поделив почленно (4.7) на (4.8) будем иметь

0,25

0, 178

1, 6 1 8

0, 11

§·



¨¸



©¹

Откуда

1,618

0, 123 .

Из уравнения (4.8) находим величину коэффициента А

0,123

0,25 0,25 0,127

500

0, 11 R e 0, 11 0, 236

HH H

§·

  

¨¸

©¹

. (4.9)

Различие в выражениях (4.6) и (4.9) для расчета коэффициента

А объясняется тем, что в первом случае не были сделаны необходи-

мые алгебраические преобразования:

153

0,127

0, 127 0, 627 0,127

0,627

10 0, 236

10 4, 24





Среднеквадратичная погрешность аппроксимации В. Д. Бело-

усова по сравнению с формулой Альтшуля составляет около 5 %.

Связано это, в частности, с тем, что ее автор не стремился сделать

погрешность вычислений минимальной, а исходил из условия ра-

венства коэффициентов λ на границах зоны смешанного трения и

соседних зон.

Автору этих строк совместно с аспиранткой Н. В. Морозовой

удалось свести уравнение Альтшуля к виду (4.5) со среднеквадра-

тичной погрешностью 2,6 %. Опишем, как это было сделано.

Представим формулу Альтшуля в виде



0,25

0, 11 68

0,25



(4.10)

Недостатком данной записи является то, что расчетный коэффи-

циент 0,11·(68 + ε · Re)

0,25

является функцией числа Рейнольдса. Вме-

сте с тем из формулы (4.8) следует, что в зоне смешанного трения

справедливо неравенство

Re10 500.

d d

Задаваясь значениями ε · Re в этом диапазоне, сначала рассчита-

ли величины функции 0,11 · (68 + ε · Re)

0,25

, а затем, используя метод

наименьших квадратов, заново описали полученные точки выраже-

нием 0,206· (ε · Re)

0,15

Подставив его в (4.10), получили искомую зависимость

0,15

0,1

0, 206



(4.11)

Из нее видно, что в зоне смешанного трения турбулентного ре-

жима величины коэффициентов А и m равны 0,206 · ε

0,15

и 0,1 соот-

ветственно. Среднеквадратичная погрешность расчетов по формуле

(4.11) относительно формулы Альтшуля — менее 3 %, что меньше,

чем по другим известным аппроксимациям.

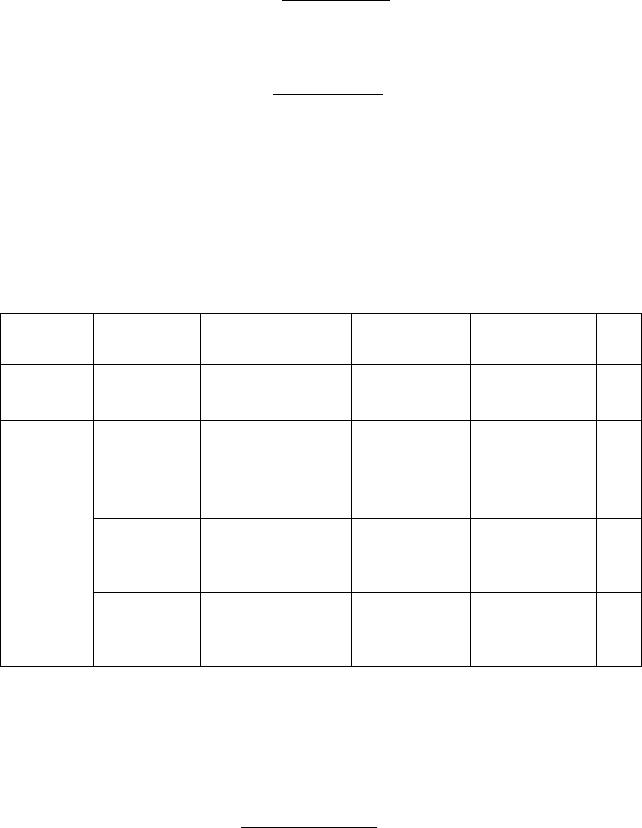
154

В тех случаях, когда необходимо, чтобы зависимость потерь на-

пора на трение от расхода Q была выражена в явном виде, удобно

использовать обобщенную формулу Лейбензона





(4.12)

где β — расчетный коэффициент, равный





Формула (4.12) получается подстановкой выражения (4.9) в фор-

мулу Дарси — Вейсбаха (4.3).

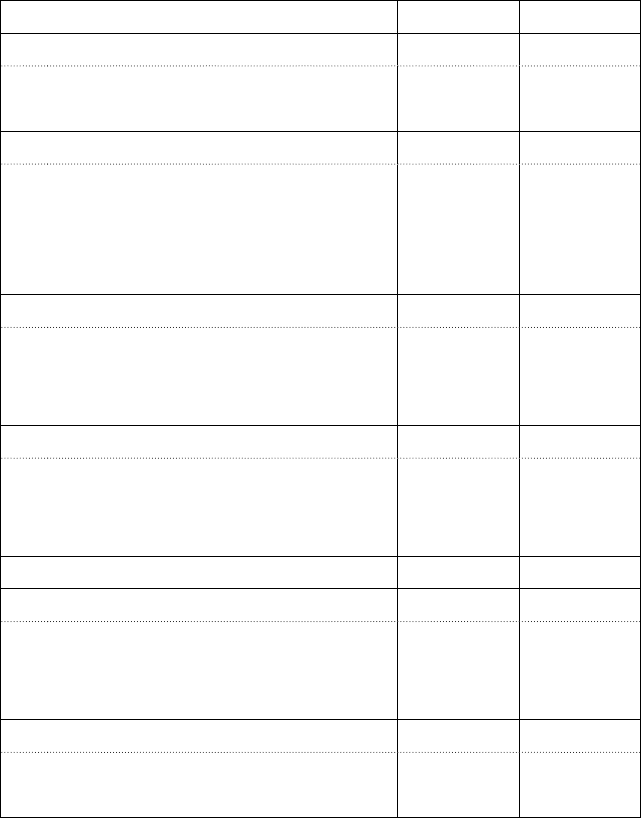
Сводная таблица величин коэффициентов А, β и m в формуле

(4.9) приведена ниже (табл. 4.7).

Таблица 4.7 — Рекомендуемые величины коэффициентов

А, β и m

Режим

течения

Зона

трения

Область

использования

Аβm

Лами-

нарный

—

Re < 2320

64 4,15 1

Турбу-

лентный

Гидрав-

лически

гладкие

трубы

2320 ≤

Re < Re

0,3164 0,0246 0,25

Смешан-

ного тре-

ния

≤ Re < Re

0,206 · ε0,15 0,0166 · ε0,15

0,1

Квадра-

тичного

трения

Re > Re

0,11 · ε0,25 0,0091 · ε0,25

Для вычисления потерь напора на трение при течении нефте-

продуктов, проявляющих вязкопластичные свойства, можно вос-

пользоваться уравнением Букингема (в виде аппроксимации, полу-

ченной проф. В. Е. Губиным)





' 

(4.13)

155

где ∆Р — перепад давления при течении вязкопластичной жидко-

сти со средней скоростью W в трубопроводе диаметром D и длиной

L; η — пластическая вязкость; F(И) — расчетная функция

()



ИИ И

F219

ªº



¬¼

;

И — число Ильюшина, И = τ

· D/η · W; τ

— начальное напряжение

сдвига.

Поделив левую и правую часть (4.13) на ρg и имея в виду, что

ΔP/ρg = h

, а W · D · η · F(И)/ρ = Re

, можем переписать данное выра-

жение как

Re 2





(4.14)

где Re

— число Рейнольдса для вязкопластичной жидкости.

Нетрудно видеть, что потери напора на трение в данном случае

также могут быть определены по формуле Дарси — Вейсбаха, в ко-

торой коэффициент гидравлического сопротивления λ вычисля-

ется как при ламинарном режиме. Отличие заключается в методи-

ке расчета числа Рейнольдса. Кроме того, для высоковязких нефтей

и нефтепродуктов критическое число Рейнольдса следует прини-

мать равным 2000.

Потери напора на местные сопротивления

Данный вид потерь напора определяется по формуле Вейсбаха

МС

]

(4.15)

где ζ — коэффициент местного сопротивления.

Величина коэффициента ζ зависит от вида местного сопротивле-

ния и режима течения.

При ламинарном режиме течения величину коэффициента мест-

ного сопротивления можно вычислить по формуле

]]



где ζ

— коэффициент местного сопротивления при турбулентном

режиме; А

— постоянный коэффициент.

Величины ζ

и А

определяются по табл. 4.8.

156

Таблица 4.8 — Коэффициенты местных сопротивлений

при турбулентном режиме течения

Вид местного сопротивления

Вход в трубу:

— с острыми краями — 0,50

— вдающуюся внутрь резервуара 30 1,00

Задвижка открытая:

— на 100 % 75 0,15

— на 75 % 350 0,20

— на 50 % 1300 2,00

— на 25% 3000 20,0

Вентиль стандартный:

— D

= 80…100 мм 3000 4,0

— D

= 150…200 мм — 4,7

— D

= 250…300 мм 5000 5,3

Обратный клапан:

— D

= 80…100 мм — 8,0

— D

= 150…200 мм — 4,0

— D

= 250…300 мм — 2,0

Компенсатор сальниковый — 0,2

Компенсатор П-образный:

— D

= 50…100 мм 5000 2,2

— D

= 200…300 мм — 2,4

— D

= 400…500 мм — 2,8

Фильтр для нефтепродуктов:

— светлых — 1,70

— темных — 2,20

157

4.5. Особенности гидравлического расчета технологических

трубопроводов нефтебаз

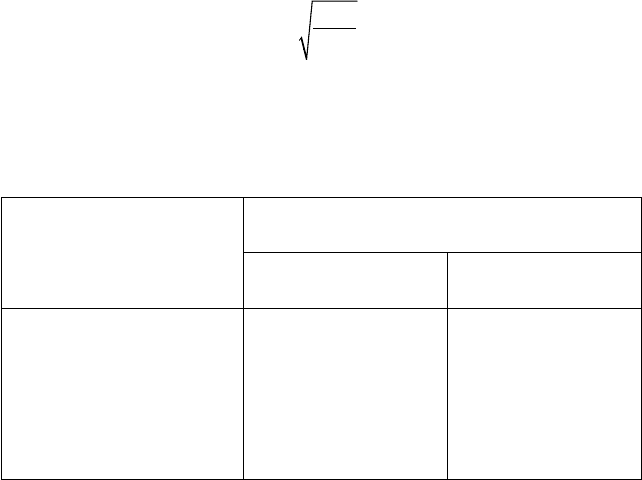
При проектных расчетах ориентировочный внутренний диа-

метр трубопроводов находится по формуле

(4.16)

где W

— рекомендуемая средняя скорость перекачки нефтепродук-

та (табл. 4.9)

Таблица 4.9 — Рекомендуемые значения средней скорости

перекачки нефтепродуктов

Кинематическая

вязкость нефтепродукта,

мм

/с

Средняя скорость,

м/с

на линии всасывания

на линии

нагнетания

менее 11,5

от 11,5 до 27,7

от 27,7 до 72,5

от 72,5 до 145,9

от 145,9 до 438,5

от 438,5 до 877,2

1,5

1,3

1,2

1,1

1,0

0,8

2,5

2,0

1,5

1,2

1,1

1,0

Найденные ориентировочные значения диаметров округляются

в большую сторону до ближайшего значения.

При правильно выбранных размерах трубопроводной комму-

никации общее время слива-налива нефтепродуктов должно быть

меньше нормативного.

Особенностью трубопроводов нефтебаз является их относитель-

но небольшая длина, разветвленность, большое количество мест-

ных сопротивлений, а в отдельных случаях (коллекторы) и перемен-

ность расхода по длине.

Расчет потерь напора в простом трубопроводе

Простым называют трубопровод постоянного диаметра с неиз-

менным расходом по длине.

158

В отличие от магистральных трубопроводов в условиях неф-

тебаз потери на местных сопротивлениях нельзя принимать рав-

ными 1…2 % от потерь напора по длине. Необходимо, пользуясь

технологической схемой, пересчитать все виды местных сопротив-

лений, рассчитать потери на каждом из них, используя величины

коэф фициентов местных сопротивлений, а затем найти суммарные

потери h

мс

Выразим величины потерь напора на трение по длине и на мест-

ных сопротивлениях через величину расхода

WQQ

hW fQ

Dg D gD

22 5

;





 



мс

ggD

]



где f

— гидравлический уклон при единичном расходе,

;





ζ — сумма величин коэффициентов местных сопротивлений на рас-

сматриваемом участке трубопровода длиной ℓ и диаметром D.

Соответственно, общие потери напора на трение по длине и на

местных сопротивлениях на рассматриваемом участке технологичес-

кого трубопровода составят

мс пр

hh h fQ f Q

]





  



(4.17)

где f

пр

— приведенная величина гидравлического уклона при еди-

ничном расходе,

пр

]







 l

. (4.18)

Расчет суммарных потерь напора с использованием формулы

(4.16) удобен тем, что данное выражение можно решать совместно

с уравнением характеристики центробежных насосов (или насос-

ных станций) для нахождения фактического объемного расхода

159

в технологическом трубопроводе. Неизвестные заранее величины

λ и ζ при этом следует вычислять, используя число Рейнольдса Re

соответствующее рекомендуемой скорости, т. е.

po p

Wd QW

QQS



Если для расчета потерь напора на трение используется форму-

ла Лейбензона, то

hfQ



 l

(4.19)

где f — гидравлический уклон при единичном расходе,

5 – m



— коэффициент, учитывающий вклад местных сопротивлений.

Величина коэффициента k

может быть найдена с использова-

нием выражения (4.18). По определению k

= f

пр

/ f

. Соответственно

из (4.18) получаем

DDQ

]]

OSQ





§·

 

¨¸



©¹

. (4.20)

Предложенный выше прием включения потерь на местных со-

противлениях в величину гидравлического уклона удобен при по-

строении линии остаточных напоров в коммуникациях нефтебаз,

т. к. нет необходимости увеличивать их протяженность на так назы-

ваемую эквивалентную длину местных сопротивлений.

Расчет потерь напора в сложном трубопроводе

К сложным относятся все трубопроводы, отличающиеся от прос-

тых, т. е. либо с переменным расходом, либо с переменным диамет-

ром, либо с переменными и расходом и диаметром по длине.

1 случай. Трубопровод постоянного диаметра с переменным рас-

ходом по длине (D = const; Q = vаr)

Коэффициент гидравлического сопротивления λ

на i-м участке

сложного трубопровода с расходом Q

может быть выражен через

коэффициент гидравлического сопротивления λ на участке с расхо-

дом Q. По определению

Re Q

;

§·



¨¸

©¹

160

Re Q

§·



¨¸

©¹

Поделив левые и правые половины данных выражений друг

на друга, получаем

§·

¨¸

©¹

откуда

§·



¨¸

©¹

. (4.21)

Соответственно, потери напора на трение по длине составят

ii i

hQfQ

gD gD Q Q

25 25



§·

 

¦¦ ¦ ¦

¨¸

©¹

а общие потери напора (с учетом местных сопротивлений)

iii

hfQ

QgD

[





§·

  

¦¦

¨¸



©¹

fQL

QgDLQ

[



ªº

§· §·

   

¦¦

«»

¨¸ ¨¸

 

©¹ ©¹

«»

¬¼

. (4.22)

где

— относительная длина участка трубопровода с постоянным

расходом Q

; ll

— сумма коэффициентов местного со-

противления для i-го участка; L — общая длина трубопровода.

Выражение в квадратной скобке формулы обозначим через f

пр

то есть

пр i

QgDLQ

[



§· §·

   

¦¦

¨¸ ¨¸

 

©¹ ©¹

(4.23)

что позволяет привести выражение для расчета потерь напора

в сложном трубопроводе к формуле (4.17).

При использовании для расчета потерь напора формулы (4.19)

пр



§·

 

¨¸