Koren Y. The Global Manufacturing Revolution: Product-Process-Business Integration and Reconfigurable Systems

Подождите немного. Документ загружается.

When the line is not balanced, the bottleneck machine limits the system through-

put. In this case, larger buffers are needed before and after the bottleneck machine to

reduce its probability of being blocked or starved.

Principles of Buffer Design: In order to obtain a certain throughput when the

machine failures occur at random, larger buffer spaces are needed in the following

cases:

1. When there are more unreliable machines in the line

2. When the reliability of the machines is lower

3. When a machine’s MTBF and MTTR are much longer than its operation time

4. On both sides of a bottleneck machine in unbalanced lines

5. In the middle of the line in balanced lines.

The ﬁve examples below correspo nd to these ﬁve principles.

Example 1: Consider a four-machine asynchronous serial line in which all machines

have the same operation speed and identical reliability data: MTBF ¼ 9 minutes,

MTTR ¼ 1 minute, and the machine operation time is T ¼ 1 minute. According to

Eq. (7.2), each machine has a reliability R ¼ 0.9 (90%). Our PAMS software shows

that without any buffers the system throughput is 0.72 parts/minute. To reach an

expected throughput of 0.8 parts/minute, a total of four buffer spaces are required in

the system: B1 ¼ 1; B2 ¼ 2; B3 ¼ 1. (B1 is the buffer between the ﬁrst and second

machine, B2 is the buffer between the second and the third machine, etc.) However, if

the line is expanded to eight machines with all other data unchanged, without any

buffer the system throughput is decreased from 0.72 to 0.60 parts/minute. To reach the

expected throughput of 0.8 parts/minute, the system requires 15 buffer spaces that are

spread as follows: B1 ¼ 1; B2 ¼ 2; B3 ¼ 3; B4 ¼ 3; B5 ¼ 3; B6 ¼ 2; B7 ¼ 1.

Example 2: The reliability of the machines in Example 1 is lower. Given: MTB F

¼ 5.6667 minute and MTTR ¼ 1 minute, so according to Eq. (7.2)R ¼ 0.85 (85%).

The machine operation time is T ¼ 1 minute. Without any buffers the four-machine

system can only reach a throughput of 0.62 parts/minute. To reach the expected

throughput of 0.8 parts/minute, 17 buffer spaces are required: B1 ¼ 5; B2 ¼ 7; B3 ¼ 5.

Note that a decrease in the machine reliability requires a substantial increase in the

buffer total capacity from 4 to 17 spaces.

Example 3: Consider again the four-machine case in Example 1 with reliability

R ¼ 0.9 (90%). Without any buffers the system has an integrated throughput of

0.72 parts/minute. Now let us keep the relia bility of each machine at R ¼ 90%, but

expand MTBF and MTTR by 10 times. Namely, MTBF ¼ 90 minutes and MTT R

¼ 10 minutes. Now the system throughp ut is reduced to 0.696 parts/minute when no

buffers exist in the system. Furthermore, if we expand MTBF and MT TR by 100 times

so that MTBF ¼ 900 minutes and MTTR ¼ 100 minutes (the machine reliability is

still 90%), the system throughput becomes only 0.693 parts/minute.

Principle 3 states that if the machines in the system maint ain a constant reliability,

but MTBF and MTTR are increased, the system throughput is decreased. The system

reaches a higher throughput when the breakdowns and repairs occur more frequently.

THE ECONOMICS OF BUFFERS 191

Example 4: Consider the four-machine system in Example 1, but with a machine

operation time of t ¼ 1.1 minute on the second machine. The operation time of the

other three machines remains t ¼ 1 minute. All machines still have the same reliability

data: MTBF ¼ 9 minutes, MTTR ¼ 1 minute such that R ¼ 0.9. The computation with

PAMS shows that to reach the expected throughput of 0.8 parts/minute, the system

requires nine buffer spaces in total, which are spread as follows: B1 ¼ 4; B2 ¼ 4;

B3 ¼ 1. Note that when the line was balanced the total buffer space was 4 units, and

now, with 10% increase in the operation time of one machine it is 9 units. The total

buffer space is very sensitive to imbalanced lines.

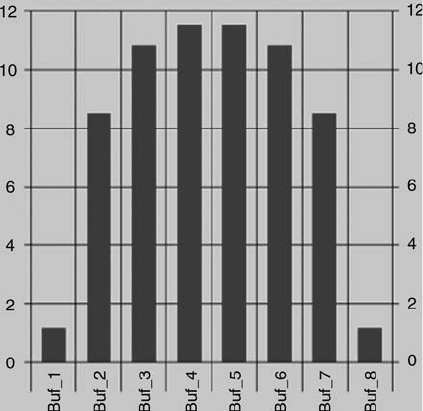
Example 5: Given a line of nine identical machines with identical reliability data and

operation speed: MTBF ¼ 7 minutes, MTTR ¼ 3 minute, and the machine operation

time is t ¼ 1 minute. According to Eq. (7.2), each machine has a reliability R ¼ 0.7.

The total given buffer capacity is 64. If the eight buffers are spread evenly among the

nine machines, their capacity between adjacent machines is 8, and the throughput is

32.16 parts/hour. If, however, the buffers are spread as in Figure 7.10, the throughput

is 33.87 parts/hour—an improvement of 5.3%. The buffers at the two ends are small,

because the ﬁrst machine will be never starved and the last machine will be never

blocked.

7.5 BATCH PRODUCTION

In large manufacturing systems, the production is done in operational stages. A stage

may be a machine, several machines in parallel, an assembly station, a chemical

Figure 7.10 Larger buffer capacities at the middle of the line increases its throughput.

192

ECONOMICS OF SYSTEM DESIGN

process, etc. At each stage several manufacturing tasks are performed. When the tasks

in a stage are completed, the product is transferred to the next stage, and simulta-

neously the product that was in the previous stage is transferred forward. In the last

stage, the ﬁnished products (or parts) are exiting the system at an average time, T.

Ideally, the processing times in all stages should be equal, and then the manufactur-

ing system (or line) is perfectly balanced. A perfectly balanced system has the highest

throughput, since time is not wasted on products occupying machines and waiting

(“blocked”) to be proce ssed in the next stage, and machines are not waiting for parts

(“starving”). The calculations in which various manufacturing tasks are assigned to

stages with the aim to balance the system are called line balancing.

In ﬂexible manufacturing systems that produce more than one product type, the

processing is done in batches, where each batch produces one type of identical

products that need equal processing times. Switching from one product type to

another requires time to change tools and ﬁxtures, and in many cases, time is also

needed to purge the manufacturing system from the old products. The sum of all these

times is the switchover time (t

We deﬁne below basic terms utilized in operations planning of manufacturing

system.

Throughput The average output of a production machine or system,

measured in parts per unit time

Cycle time (T) The actual average time interval between successive parts

exiting a manufacturing system, measured in time units

Cycle time ¼ 1/Throughput

Switchover time The total time needed to switch production on a ﬂexible

system from a batch of one part to a batch of another part

Makespan The total amount of time needed to produce a ﬁxed

number of jobs (which may consist of several products)

Holding cost Sum of all inventory costs (physical storage space þ

possible part breakage þ possible product obsoles-

cence) that are proportional to the amount of inventory

Shortage cost The cost of losing sales; it typically occurs when demand

exceeds the capacity (namely, the rate of demand

exceeds the system throughput). However, it may also

occur when products orders are changed between the

time the production plan is made and the time its

implementation is completed

Takt time The total time available during a production period,

divided by the demand for that period. It is the desired

time between output units synchronized to the rate of

customer demand

WIP Work-in-process, which is the sum of all parts present in a

manufacturing system between its start and end points

Throughput time The average time it takes one part to move all the way

through a manufacturing system from start to exit (also

called lead time)

BATCH PRODUCTION 193

7.5.1 Flexible System Makespan

A typical ﬂexible manufacturing system produces multiple types o f p roducts o f t he

same product family. The time to complete the production of all products is called

makespan. The products are produced in batches; the numbe r of produ ct s in the

batch is the lot size. Switching from one type of batch to another requires a

switchover time.

Tobe moreﬂexible there is aneed to switchbetween product types at high frequency.

However, in each switchover a production time is lost, so, in the end of the production

period (e.g., a day) a smaller numberof products ismanufactured, and therefore the cost

per product becomes higher. Th e calculation of this cost is presented below.

Notations:

T ¼ total given time period for production and switchovers (e.g., 16 hours)

¼ cycle time (time to complete production of one product)

¼ switchover time between product types

m ¼ number of switchovers within the given time period T

L ¼ lot size

We assume equal cycle time for products in the family and equal lot size for each

product type. The time spent on all switchovers during T is mt

and therefore the

production time is Tmt

. The number of products, n , produced during the time is

n ¼

Tmt

ð7:3Þ

The lot size is

L ¼

m þ 1

Tmt

ðm þ 1Þt

ð7:4Þ

We assume production of two types of products. The maximum lot size is obtained

with one switchover, namely for m ¼ 1,

max

Tt

ð7:5Þ

From Eq. (7.4), we can obtain

m ¼

TLt

þ Lt

ð7:6Þ

and therefore

m þ 1 ¼

T þ t

þ Lt

ð7:7Þ

194 ECONOMICS OF SYSTEM DESIGN

The product manufacturing cost, y, is the sum of the ﬁxed costs (C

) per product

and the variable costs (C

y ¼ C

þ C

=n ð7:8Þ

where, from Eq. (7.4), n ¼ Lðm þ 1Þ. Substituting (m þ 1) from Eq. (7.7) into

Eq. (7.8) yields

y ¼ C

þ Lt

T þ t



ð7:9Þ

To obtain the cost as functi on of the relative lot size, L

¼ L=L

max

, we divide the

numerator and denominator of Eq. (7.9) by L

max

, which yields

y ¼ C

þ 2t

=ðTt

ðT þ t

ÞL

ð7:10Þ

Eq. (7.10) is valuable at the design stage of ﬂexible systems that will produce

multiple products. If the system is designed for the minimum number of switchovers,

the lot size is the maximum possible according to Eq. (7.5), and the cost is minimal.

However, if because of practical operations requirements there will be a need for

additional switchovers, the system capacity would not be able to meet demand.

Therefore, it is more economical to design the capacity of ﬂexible systems with lot

sizes smaller than the maximum as long as it does not increase substantially the cost of

producing the products.

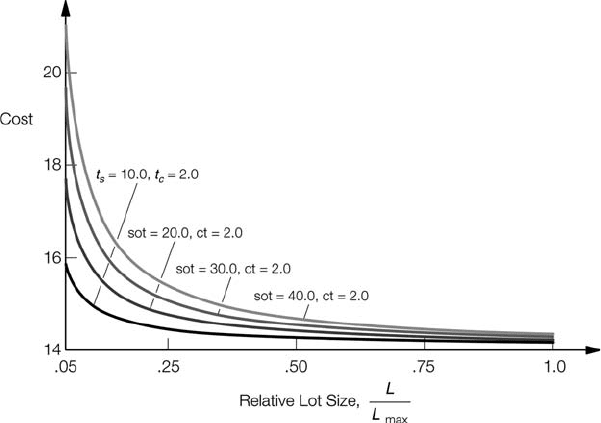
Figure 7.11 shows an example of a part that requires a cycle time of 2 minutes for its

production, and required switchover times between product types (sot or t

) of 10, 20,

30, and 40 minutes (typical values in the powertrain industry). In this example

T ¼ 960 minutes (equals 16 hours or two shifts), C

¼ 2000, and C

¼ 10. If the

switchover time is small (10 minutes) compared with the cycle time, designing the

system capacity with lot sizes of 0.25 L

max

has a very insigniﬁcant impact on the cost,

but allows more ﬂexibility when operating the system. However, when the switchover

time is large (40 minutes) compared with the cycle time, a lot size of 0.75 L

max

recommended for designing the system capacity.

7.5.2 Minimizing Irresponsiveness to Customer’s Demand

When producing simultaneously multiple product types, a typical optimization

measure for the sequencing of products is minimizing makespan, which is achieved

by the production of large lot sizes.

This operation policy assumes that customer’s

orders will not change after the production started, and that severe disruptions will not

occur. However, in “lean” environments, where customer orders are typically ﬁlled

through new production rather than from inventory, minimizing makespan by

BATCH PRODUCTION 195

producing large lot sizes may create a product shortage. As a result, manufacturers are

losing sales, and consequently might also lose their customers.

We observed a shortage issue in which products were not ready to be supplied when

needed in an engine machining line that produced two types of engine blocks, A and

B, in large lot sizes with one switchover (which takes about 40 minutes) during the

working period. The line scheduled to produce part A in the ﬁrst 8 hours, switch over,

and continue to produce part B. Because of disruptions up stream in the car assembly

process, the order was changed during the day—the line was instructed to supply

immediately type B engine blocks, which had to be produced later in the day. Since

engine blocks of type B were not available, a shortage occurred. This sort of changes

in orders during production is becoming more common in a variety of industries.

Customer’s orders may change even after the production has already begun.

We observed such production environment in a 1999 visit to Intel’s Fab-8, which

produced simultaneously 40–60 types of wafers. The production of a wafer takes about

6–7 weeks. During this long period customers are changing their order quantities; but

even though, Intel supplies the modiﬁed ordered quantities on time.

Manufacturing systems cannot be primarily designed based on demand forecasts

without concern for changes in customer orders. The competitiveness of today’s

global economy necessitates focusing on the manufacturing system responsiveness to

customers. To be responsive to customer’s needs, the manufacturing system should be

designed with enough capacity to operate with policies that satisfy customers’

demand (e.g., adjusting lot sizing, and allowing an optimal number of switchovers).

The manufacturer’s dilemma is to determine an optimal lot size. On one hand, if the

lot size is too small, many switchovers occur, and potential production time is lost,

Figure 7.11 Product manufacturing cost as function of the lot size and switchover times.

196

ECONOMICS OF SYSTEM DESIGN

which may create a shortage of products. On the other hand, if the lot size is too large

and the customer changes orders, a shortage cost may occur, since the system cannot

produce the new orders on time, thus it is not responsive to the customer’s need.

System Responsiveness: Matson deﬁnes responsiveness as “the ability of a

production system to respond to disturbances that impact upon production goals.”

Shafaei and Brunn deﬁne customer responsiveness as whether or not the customer

demands are fully satisﬁed by the due date.

However, an analytical expression could

not be found in the literature.

We present below a calculation of a shortage cost caused by the irresponsiveness of

the manufacturing system.

The shortage cost that relates to system irresponsiveness

has two components, and a third cost component affects the product cost.

1. If the lot size is very large, a shortage, as described above in the engine block

example, may occur (i.e., a sales shortage).

2. If the lot size is very small there are many switchovers, the net production time is

smaller, and a smaller number of products is manufactured, which may also

cause a shortage (i.e., a produc tion shortage).

3. When there are many switchovers (i.e., small lot sizes), the ﬁxed costs are

divided by a smaller number of actual produced products, which, in turn,

increases the average cost per product. This cost is expressed in Eq. (7.10).

The challenge is to determine a reasonable optimal lot size that trade offs these

costs.

A very large lot size will cause a sales shortage cost, C

, due to lack of

responsiveness to order changes. The cost C

is zero when the lot size is 1 (e.g.,

the manufactur ing system is producing products in the sequence ABAB...); at lot size

of 1 the syst em has its maximum responsiveness. We assume that the sales shortage

cost caused by the slow responsiveness is given by

¼ C

ðL1Þ

ð7:11Þ

where C

is a cost coefﬁcient.

Substituting L ¼ L

max

in Eq. (7.11), with L

max

substituted from Eq. (7.5), yields

¼ C

Tt

1



ð7:12Þ

On the other hand, we calculate the shortage cost component that is caused by

producing in small lot sizes, which requires many switchovers. If the system

produces two products, there must be at least one switchover. The production

shortage cost caused by one switchover is 0. If the lot size is small, there are many

switchovers and a production time mt

is lost. The numb er of products that could be

Dr. Wencai Wang developed the calculations in this section.

BATCH PRODUCTION 197

produced during this time is mt

, and if the cost of a shortage of each product is

, then the total production shortage cost is

¼ C

ðm1Þ

ð7:13Þ

Substituting m from Eq. (7.6) yields

¼ C

ðTLt

ðt

þ Lt

1



¼ C

T L

max

þ L

max

1



ð7:14Þ

Substituting L

max

from Eq. (7.5) yields

¼ C

2TL

ðTt

þ L

ðTt

1



ð7:15Þ

The overall cost C is obtained by adding Eqs (7.10), (7.15), and (7.12):

C ¼ y þC

þC

¼ C

þ2t

=ðTt

ðT þt

ÞL

þC

2TL

ðTt

þL

ðTt

1

þC

Tt

1

ð7:16Þ

Figure 7.12 shows the changes of product cost C with the relative lot size L

. where

¼ L=L

max

and the maximum lot size, L

max

, is the lot size with one switchover during

the working period. We can see that the cost tradeoffs cause an almost ﬂat minimum

cost that is insensitive to the lot size in the range: 0.75 L

max

> lot size > 0.25 L

max

When the system produces two products, A and B:

An average lot size of 0.75 L

max

, actually means operating with two switchovers

(SWO), and the producing schedule is: half As, SWO, all Bs, SWO, half As.

A lot size of 0.5 L

max

means operating with three switchovers, and the producing

schedule is: half As, SWO, half Bs, SWO, half As, SWO, half Bs.

A lot size of 0.25 L

max

means operating with seven switchovers, and the

producing schedule is: 1/4 As, SWO, 1/4 Bs, SWO, 1/4 As, SWO, 1/4 Bs,

SWO, 1/4 As, SWO,1/4 Bs, SWO, 1/4 As, SWO, 1/4 Bs.

When planning the capacity of a new manufacturing system and the switchover

time is long, the capacity should be designed to accommodate at least two daily

switchovers. When the switchover time is short, the system’s planned capacity

should allow for not more than seven daily switchovers. There is no substantial

beneﬁt in operating a system with more than seven switchovers.

198 ECONOMICS OF SYSTEM DESIGN

A short switchover time is deﬁned around one hundredth of a production period

(e.g., 10 minutes when the planned produc tion period is 16 hours). A long switchover

time is about four times longer.

7.6 OPTIMAL CUTT ING SPEEDS

Determining the right machine speed of each machine in a system has a profound

effect on the system throughput. The following example demonstrates that the

considerations in selecting machine speeds are different when a stand-alone machine

is operated and when the machine is integrated into a system (of two machines in this

case).

A part has to be machined on a single machine tool and you have to recommend a

cutting speed. If the cutting speed is higher, more parts are machined before a tool

change, but the tool life deteriorates exponentially as the speed becomes higher. The

tool life data are given in the table below.

Cutting speed (m/minute) 150 238 300 513 600

Tool life (minute) 480 120 60 12 7.5

Time to machine one part 12 7.5 6 3.5 3

The tool changing time of worn tools is on average 5 minutes.

Figure 7.12 Cost as function of the lot size for various switchover times. Parameters used

to obtain the chart are: C

¼ 2000, C

¼ 10, C

¼ 80, C

¼ 150, k

¼ 0.9.

OPTIMAL CUTTING SPEEDS 199

The plant is working in two shifts, each of 8 hours, with 1-hour break between

shifts.

(a) Calculate the number of tools needed and the number of parts machined in

8 hours at each of the above ﬁve speeds. What is your recommendation for a

cutting speed?

At speed of 150 m/minute, the number of tools needed in 8 hours is

860

480

¼ 1.

The number of parts machined is 1 

480

¼ 40.

At speed of 238 m/minute, the number of tools needed is

860

120 þ 5

¼ 3.

The remaining time to the end of the shift after the last tool change is

8  603  125 ¼ 105 minutes.

The number of parts machined is 3 

120

7:5



8603125

7:5



¼ 48 þ 14 ¼ 62.

At speed of 300 m/minute, the number of tools needed is

860

60 þ 5

¼ 7.

The remaining time to the end of the shift after the last tool change is

8  607  65 minutes.

The number of parts machined is 7 

860765



¼ 70 þ 4 ¼ 74.

At speed of 513 m/minute the number of tools needed is

860

12 þ 5

¼ 28.

The remaining time to the end of the shift after the last tool change is

8  6028  17 minutes.

The number of parts machin ed is 28 

3:5



8602817

3:5



¼ 84 þ 1 ¼ 85.

At speed of 600 m/minutes the number of tools needed is

860

7:5 þ 5

¼ 38.

The remaining time to the end of the shift after the last tool change is

8  6038  12:5 minutes.

The number of parts machined is 38 

7:5



8603812:5

3:5



¼ 76 þ

1 ¼ 77.

The results are summarized in the table below:

Cutting speed (m/minute) 150 238 300 513 600

Number of tools needed 1 3 7 28 38

Number of parts machined 40 62 74 85 77

If tooling cost is not consi dered, the speed that provides the highest throughput, 85

parts per shift, is 513 m/minute. However, note that 28 tools are changed during the 8-

hour shift.

Now, let us see how this recommended speed changes when the machine is part

of a small system composed of two machines. The machined parts are transferred

to the next manufacturing operation that requires 6.5 minutes per part. The machine

of this operation is fully automatic and tools are changed on this machine once

per day.

200 ECONOMICS OF SYSTEM DESIGN